周期性有砟轨道结构垂向弯曲振动波复频散分析

徐 伟

（中铁二十五局集团有限公司，广东 广州 510600）

列车和轨道接触产生的振动，既可能对钢轨结构造成损伤，影响列车的运行安全，又会产生辐射噪声对沿线居民的生活带来影响。因此，振动控制一直是轨道交通中迫切需要解决的问题之一[1]。振动是以弹性波的形式在结构中传播的，研究轨道结构振动传播规律对于轨道结构的振动控制具有重要意义。

轨道结构可视为由相同的结构单元沿纵向规律排布的周期性结构。周期性特征对于内部振动波的传播具有滤波特性，在特定的频率范围内弹性波因为衰减而无法在结构中传播，也被称为带隙特性[2]。对轨道结构开展频散分析对于了解其振动传递特性具有重要意义。频散分析从波传播的角度，仅建立一个周期单元的分析方式，因此具有直观、建模工作量小、计算效率高等优点。频散分析也成为了研究轨道结构传播规律以及轨道结构振动控制的重要分析方式[3-6]。

频散分析根据其计算模式的不同，可以分为实频散和复频散。实频散是通过给定实波数，求解频率，这种模式求解思路清晰，能够得到弹性波的传播特性，但无法知道衰减。求解实频散的方法很多，常见的求解方法有传递矩阵法[7]、平面波展开法[8]、有限元法[9]、能量法[3，10]等。然而在实际的轨道结构中，往往需要得到结构的衰减特性来判断减振性能，而这是实频散所不能反映的。复频散是通过给定频率，求解复波数。相比于实频散而言，通过复频散结构能够直接获取周期轨道结构波的衰减规律，在进行阻尼、频变效应分析时更加直观，具有更大的应用价值。

复频散是通过频率求解波数，这在传统的频散求解方式中是一种逆向求解问题，会导致原本简单的线性问题转化为非线性问题，因此求解难度大。相比于实频散，复频散的求解方式相对较少。目前，复频散的主要求解方法有传递矩阵法[5]，平面波展开法[11]和有限元法[12]等。这些方法在各自领域中都有较好的使用，但也有着各自的局限性。传递矩阵法的传递矩阵中不含有波数，因此能够简单的求解出复频散。但仅适用于简单的一维问题。平面波展开法主要用于二维周期结构的复频散求解问题，该方法思路清晰，但在组元参数速度差异较大时，收敛速度较慢；有限元法虽具有很好的几何适用性，但其计算精度依赖于网格划分精度，这不利于大量的参数扫描或参数改变。因此有必要发展一种具有良好适用性、计算效率高的复频散求解方法。

能量法可以将求解微分方程问题转化为对泛函极值问题的求解，能够简化耦合问题的计算。但传统的能量法在构建位移函数时难度较大，且其位移函数中含有波数项，在扫描波数计算的过程中，需要不断地进行重复性计算。通过引入虚拟弹簧[13]来模拟复杂结构中的各类边界条件，将约束转化为虚拟弹簧的弹性势能，使得波数项仅存在于周期边界的弹性势能，再将弹性势能中的含波数项与无波数项分离，便可以通过给定频率求解得到复频散。本文将基于能量法，结合虚拟弹簧模型，提出一种新的复频散结构求解方法。并利用该方法对周期性有砟铁路轨道结构垂向振动弯曲波的复频散阻尼效应、频变效应进行分析。

1 理论计算

根据文献[13]，通过引入虚拟弹簧模型来模拟复杂的边界耦合条件，约束便转化为了系统中的弹性势能，再将含有波数项的虚拟弹簧刚度矩阵与不含波数项的矩阵分开，在每次扫描波数时，便仅需计算虚拟弹簧的刚度矩阵，无需其他冗余计算。那么，在进行频散复频散求解即根据给定频率求解波数时，将虚拟弹簧刚度矩阵中的含波数项与无波数项分开，使得复平面内复杂的非线性微分振动方程求解转化为线性方程求解特征值问题，在保证计算准确性的前提下简便计算。

1.1 有砟轨道模型论述

有砟轨道结构中主要包括钢轨、扣件、轨枕与道砟。为同时考虑剪切效应与弯曲效应且减小误差，本文将用连续Timoshenko 梁模型来表示钢轨。因本文主要分析垂向振动的波传播规律，文中扣件与道砟均被考虑为支撑弹簧与黏性阻尼的并联系统；轨枕考虑为集中质量块，如图1 所示。

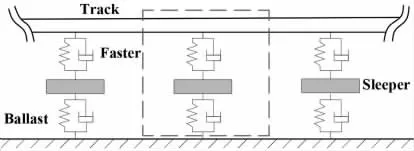
图1 有砟轨道结构物理模型Fig.1 Physical model of ballast track structure

轨道结构为沿纵向线对称的重复周期性结构，因此，本文仅取一个元胞中的单侧结构进行分析，最小周期的长度为扣件的间隔l。如图2 所示，相邻的周期单元之间设置虚拟弹簧，将转角弹簧和线弹簧同时连接上一单元的末端与下一单元的首端，二者分别用以满足转角与位移的周期边界条件。建立一个平面直角坐标系，其中沿钢轨纵向为x 轴，钢轨的垂向位移与转角分别表示为w，γ，轨枕等效为集中质量其垂向振动位移可以表示为u。根据能量法计算原理，钢轨的位移场函数由形函数f（x）和与时间相关的系数α（t）表示为

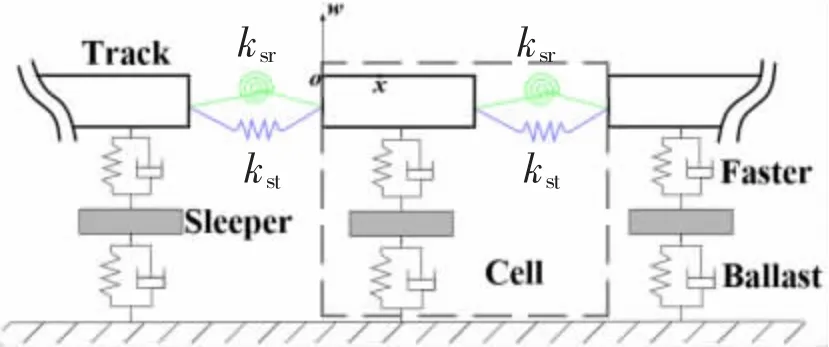
图2 有砟轨道结构计算模型Fig.2 Calculation model of ballast track structure

式中：N 为形函数的个数；上标H 为Hermite 转置；

1.2 构建能量泛函

本文的计算基于能量泛函变分原理，其中系统的总能量为系统的应变能与外力做功之和，因此，下文将对钢轨的应变能与动能、扣件的势能、轨枕的动能、道砟的势能以及虚拟弹簧的势能进行计算。轨道为沿纵向对称的结构，取一条钢轨进行分析，将钢轨考虑为Timshenko 梁，根据能量泛函变分原理，可以得到钢轨因垂向振动变形而产生的应变能、动能可以表示为

式中：UB、EB、Ab、ρb分别为钢轨应变能、动能、横截面积与密度；Ib为截面惯性矩；kb为剪切系数；Eb为钢轨的杨氏模量；Gb为剪切模量（Gb=Eb/2（1+μ），μ 为钢轨泊松比）；KB、МB分别为钢轨的刚度矩阵、质量矩阵。

本文中轨枕被等效为集中质量块，则其动能ER可由下式计算得到

式中：mr、МR分别为轨枕的等效质量、质量矩阵，O1为2N×2N 的零矩阵。

本文将扣件、有砟道床等效为支撑弹簧，扣件与道砟的垂向刚度系数可分别表示为ks1，ks2。考虑扣件及道砟的阻尼效应时，扣件刚度和道砟刚度采用复刚度形式，则二者的刚度可以表示为=kf（1+iηf），=ks(1+iηs) ，其中ηf和ηs分别为扣件和道砟的阻尼损耗因子，则其垂向弹性势能为

式中：Ks1，Ks2分别为扣件与道砟的弹性势能矩阵。

本文选择虚拟弹簧模型来模拟轨道结构满足周期性结构的条件，各元胞结构之间的虚拟弹簧都需要满足沿x 轴的位移与转角条件，kx为沿x 轴波数，则x 轴约束条件与虚拟弹簧的弹性势能可以表示为

式中：Usp为道砟势能；kst，ksr分别为虚拟弹簧的位移与转角系数；Ksp为扣件的刚度矩阵。令λ=e-ikxl，则可以得到虚拟弹簧的刚度矩阵为

综上，该模型单个周期单元的系统总能量泛函便可以得到，再由Lagrange 方程可得

式中：M=MB+MR。那么，通过扫描波数kx，并对式（11）特征值求解就可以得到轨道结构的实频散。

1.3 复频散计算

复频散的求解模式频散是通过已知频率，得到对复波数，这是一种逆向求解问题。此时边界条件约束内存在未知波数kx时，直接求解复平面内的非线性问题计算较为复杂。因此，为解决这一难题，把虚拟弹簧刚度矩阵Ksp中的含有波数项与不含波数项分开，便能够将非线性微分振动方程求解转化为易于求解的线性方程求解特征值问题，可以得到

而后，将上式代入式（10），整理可以得到

为便于求解，再针对上式运用降阶法，令λα=η，即λα-η= 0，可以得到

由于频率ω 是已知的，那么通过对上式进行特征值求解即可求得λ，则复波数kx也可得到，进而得到结构频散复频散。

2 数值分析

本文采用虚拟弹簧来模拟周期边界条件约束，弹簧刚度系数的理论值应趋于无穷大，但在实际计算中无法达到，须取一个相对大的值代入计算，但取值过大又会超过计算机的计算量程导致计算结果出错，若是取值偏小则无法达到准确性要求。其次，矩阵维度即形函数的个数越多钢轨形变位移的拟合效果越好，但过多也会增加计算成本。因此，矩阵维度与虚拟弹簧刚度的取值很大程度上影响着计算的速度与准确性。

2.1 收敛性分析

考虑到计算中矩阵维度和虚拟弹簧刚度系数对计算效率性和结果精确性的影响，本节将以图1为结构对象，随机选取3 条频散曲线，采用控制变量法，分析在N，kst，ksr取不同值时波数的收敛性，后二者因数值取值可以相同，统一以ksp替代。有砟轨道结构模型的各项参数见表1[5]。

表1 双层有砟轨道结构模型材料参数Tab.1 Material parameters of double-layer ballasted track structure model

由图3 可知，在形函数个数N 等于9，kst=1011N/m2，ksr=1011N/rad 时，各阶对应波数的数值已经明显稳定，那么可以认为实际计算所求得的解便已经收敛，后续计算也使用此参数。

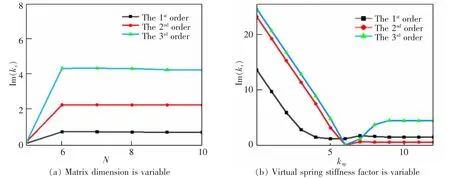
图3 有砟轨道结构模型收敛性分析Fig.3 convergence analysis of ballast track structure model

2.2 准确性验证

为和既有文献进行对比，在本节中，将扣件与道砟的阻尼均考虑为0，对有砟轨道模型的复频散进行求解，具体结果如图4 所示，其中灰色标注区域即是计算所得的频散带隙范围。

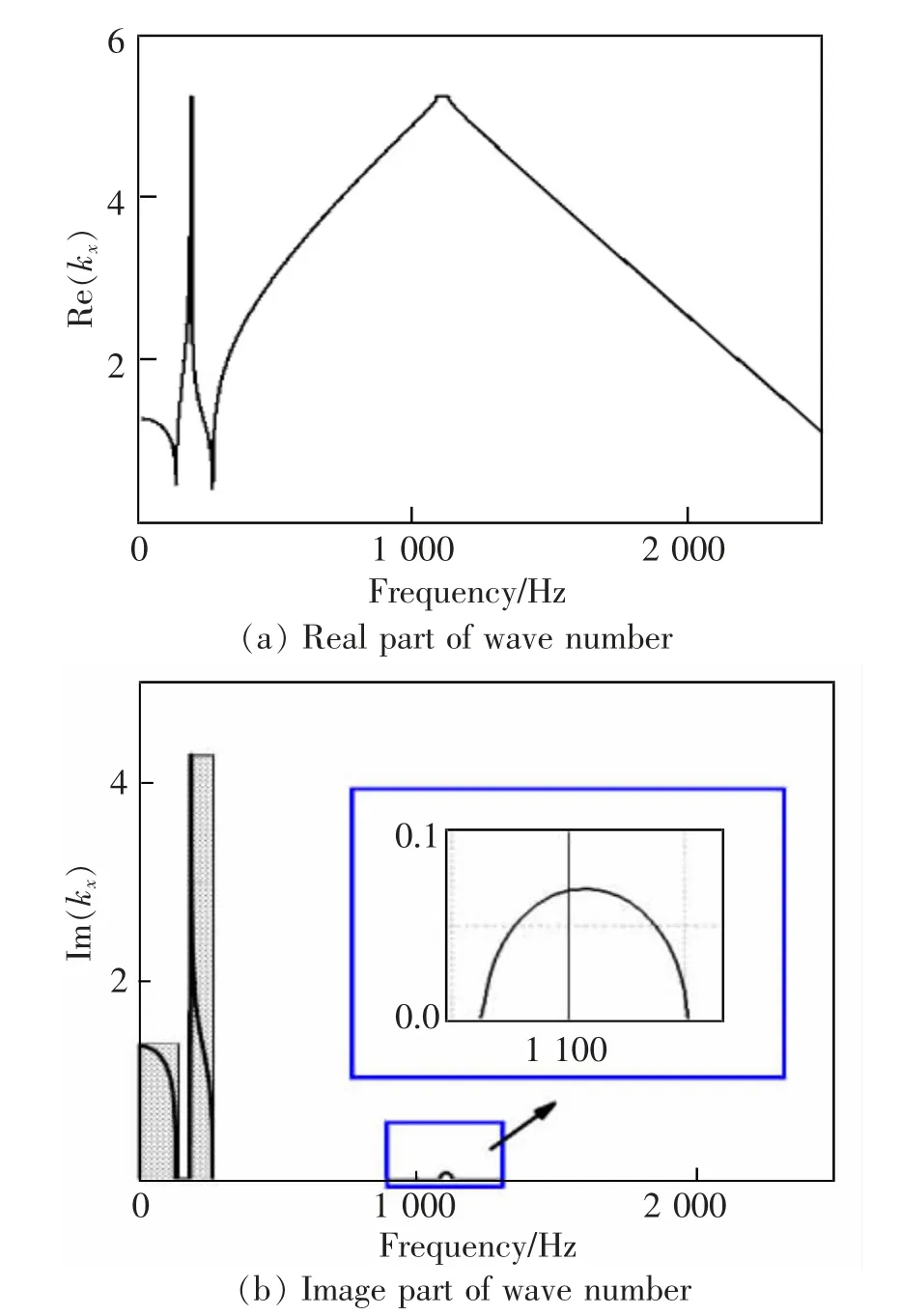
图4 有砟轨道结构频散曲线图Fig.4 Frequency dispersion curve of ballasted track structure

由图3 可见，在0～2 500 Hz 内，三段带隙的范围分别为：0～130 Hz，181～262 Hz，1 080～1 127 Hz，与文献[5]中实频散的各阶带隙结果吻合度较高，各段的带隙起始、截止频率的对比如表2，验证了本文方法的准确性。

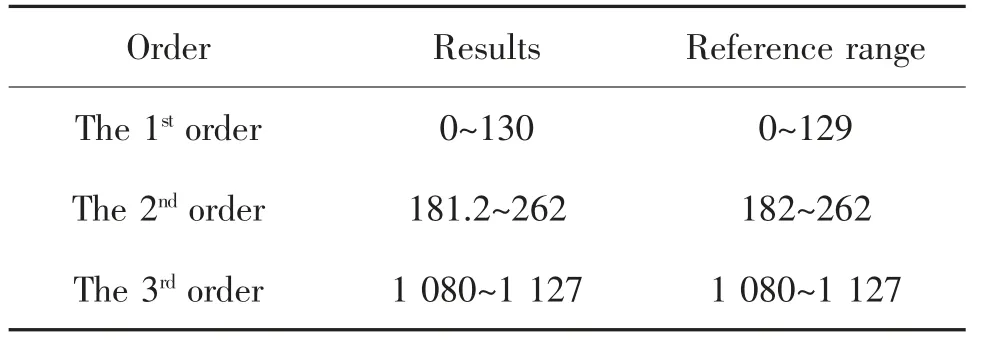
表2 有砟轨道模型带隙范围对比Tab.2 Comparison of band gap range of ballasted track modelHz

3 复频散特性分析

在实际轨道结构中，材料往往具有阻尼效应和参数的频变等。这对轨道结构中波的传播影响是实频散的求解模式难以体现的。相较于实频散而言，复频散能够更直观地表示带隙内波的衰减规律，便于观察参数频变及阻尼效应等对带隙的影响，本节就将从这两方面进行分析。

3.1 刚度频变效应分析

由图1 可以看到，扣件是轨道结构的重要弹性支撑、减振元件，其主要支撑性能源自于扣件系统中的高分子黏弹性材料垫板，而弹性垫板的动刚度又受频率的影响[14-15]。在实频散计算中，频率作为因变量不能进行频变效应的分析；与之相反，复频散计算中的频率为自变量，十分便于我们分析扣件刚度的频变效应。Maes 等[16]测量了在20～2 500 Hz 内弹性垫板的动刚度与频率的关系，发现二者具有密切地线性相关性，且可由下式拟合

式中：kdsp为扣件的动刚度；f0取4 Hz，为起始刚度；kf取25 kN/mm，其中，kf可以认为是扣件的静态刚度。图5 为弹簧刚度与频率的变化曲线图。

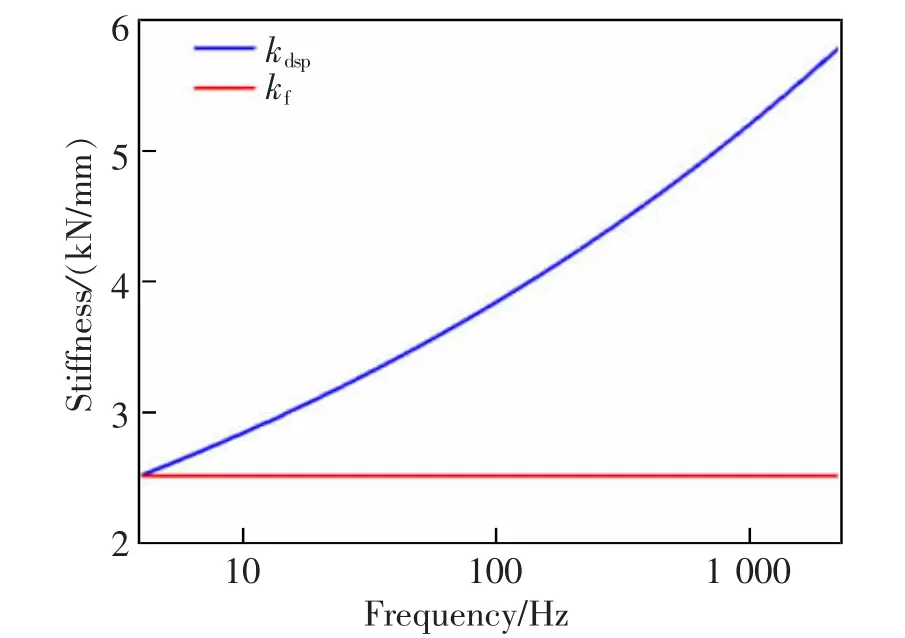
图5 弹簧刚度与频率的变化曲线Fig.5 Variation curve of spring stiffness versus frequency

有砟轨道的其他参数取值和表1 中一致。图6是频变效应对有砟轨道复频散曲线的影响对比。从图6 中可以明显看到，在2 000 Hz 内，随着扣件刚度的增加，带宽与衰减能力均相应地增加，频散曲线整体向高频移动。但第一阶带隙受刚度的影响相对较小，这是因为此时的刚度变化不大。第二、三段频散的虚部（反映结构衰减）受刚度的影响较大，这与其形成机理有关。第二段带隙形成是钢轨与轨枕之间的共振所致，因此刚度影响剧烈。扣件刚度的增加使得更大频率范围的弹性波向下传播，从而带宽增大。第三段带隙是布拉格散射所致，该段频率与晶格长度有关，其带宽与扣件的刚度相关。综上，上述的频变效应会导致低估衰减域的宽度，因此频变效应对振动传播的影响是不可忽视的。

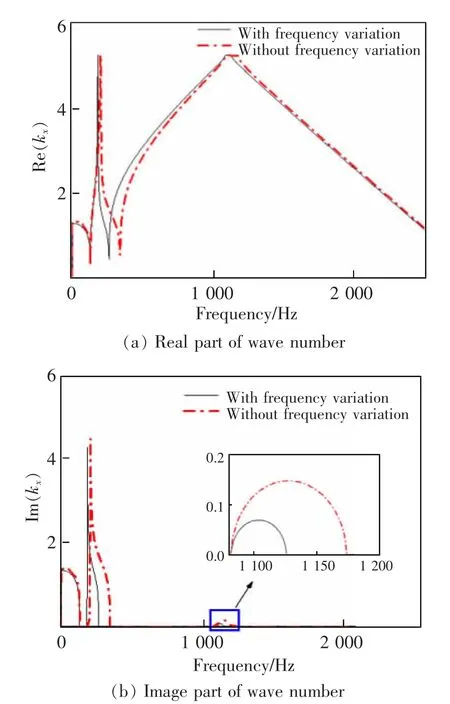
图6 有砟轨道结构扣件刚度频变效应频散曲线图Fig.6 Dispersion curve of ballast track structure fastenerstiffness frequency variation effect

3.2 阻尼效应影响分析

在轨下弹性垫板的阻尼参数发生改变时，扣件阻尼会随之改变，从而影响到结构振动的传播。然而在实频散计算中，阻尼往往被忽略不计，这是因为实频散无法得到带隙内部的具体衰减情况，但复频散结构是通过给定频率对波数进行逆向求解，能够直接观察到带隙内阻尼效应对波传播的影响，弥补了实频散无法直观表达带隙内波衰减特性的不足。

观察图7～图8，在阻尼参数变化时，频散曲线的实数部分无法明显看出带隙内的衰减变化趋势，频散的虚数部分更直观地刻画了禁带内波的衰减规律，更便于观察参数变化对带隙内衰减规律的影响。阻尼变化对于“pinned-pinned”频率处的作用较小，但对于局域共振带隙影响较大，使得无阻尼状况时的通带也发生了微小衰减，出现局域共振均摊化现象，带宽增大，带隙的衰减峰值降低，但结构的整体衰减能力增大，且衰减的程度随着阻尼的增加而增大。相较于扣件阻尼而言，道砟阻尼的增加对有砟轨道结构的影响更为剧烈。

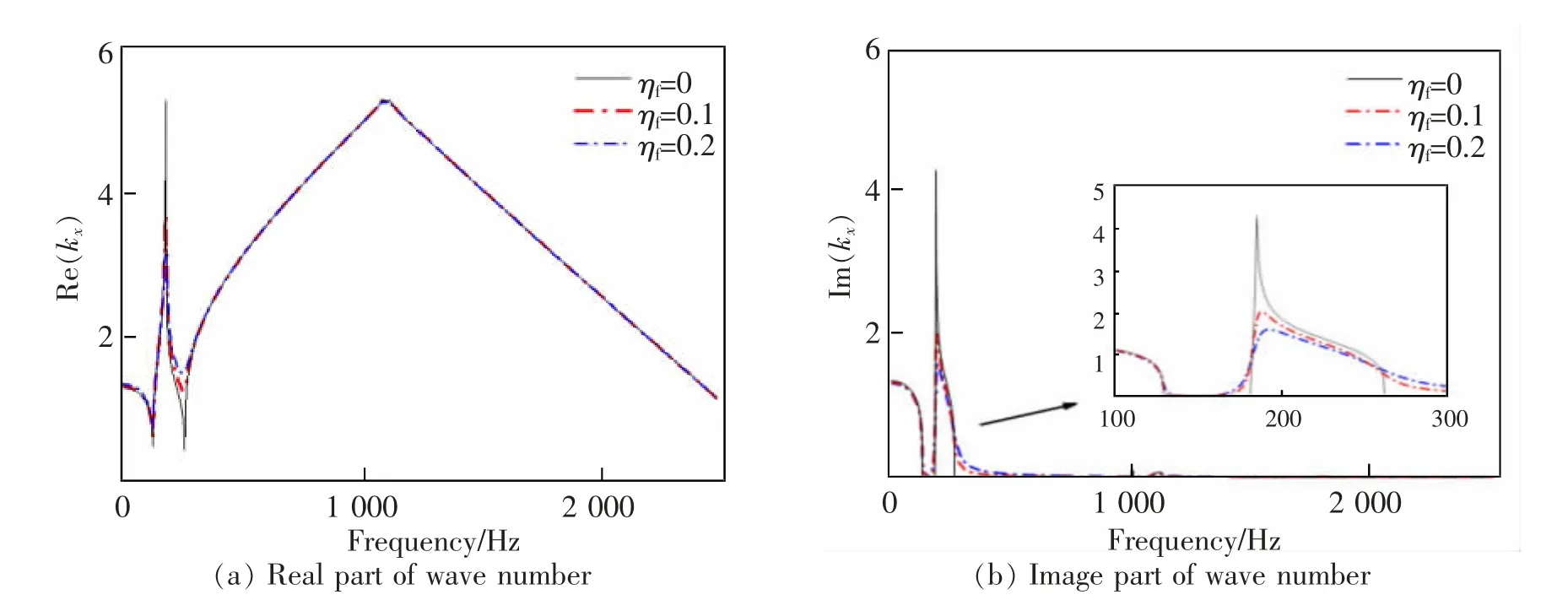
图7 有砟轨道结构频散曲线随扣件阻尼变化关系图Fig.7 Ballast track structure dispersion curve with fastener damping

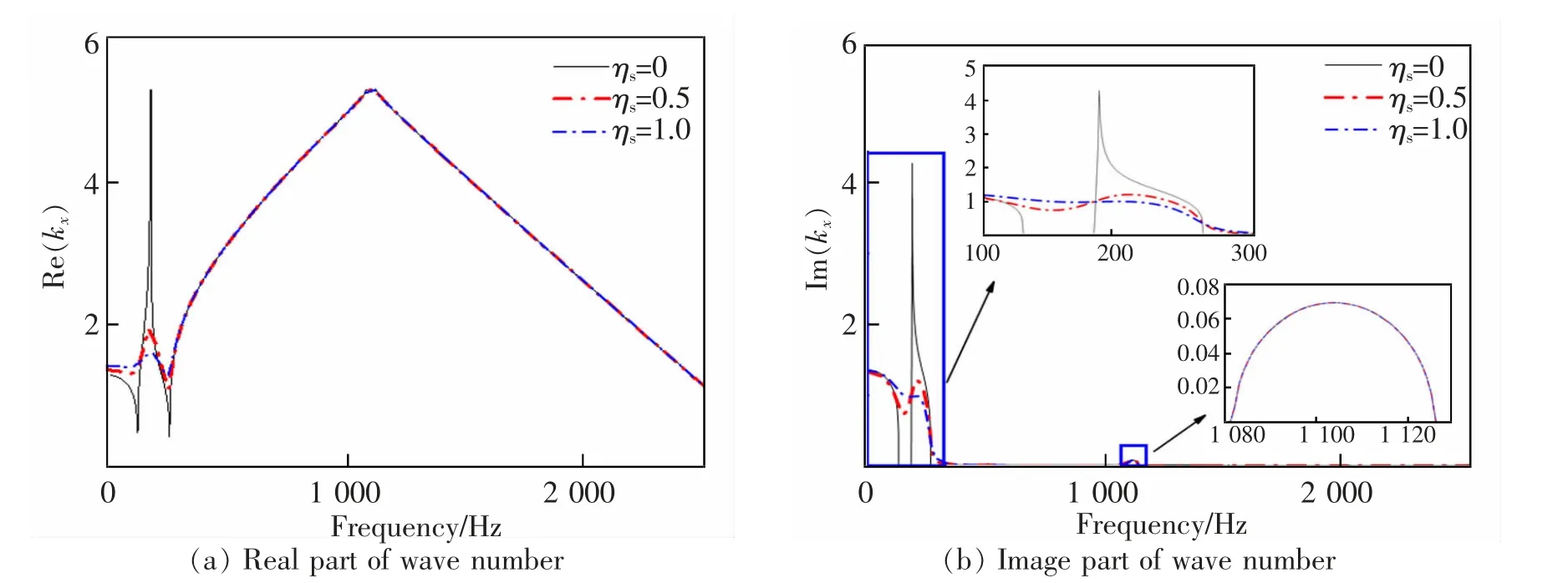
图8 有砟轨道结构频散曲线随道砟阻尼变化关系图Fig.8 Ballast track structure dispersion curve with ballast damping

3.3 综合影响

根据3.1 节，3.2 节可知，不论频变效应还是材料阻尼对轨道结构的影响都是不可忽略的。而这些又是实频散所不能反应的。在实际的轨道结构中，材料阻尼和扣件减振垫的刚度频变效应是同时存在的，因此为了能够更加贴合工程实际，在本节中，我们将研究阻尼和频变效应叠加时对频散曲线的影响。

此时扣件的频变效应的变化趋势参考式（14），且f0取4 Hz，kf取25 kN/mm；扣件的阻尼ηf取0.2；道砟的阻尼ηs取1.0。其他参数取值和表1 一致。

图9 为不考虑任何效应和两者都考虑的复频散曲线对比图。如图9 所示，综合考虑阻尼和频变效应对复频散的实数部分和虚数部分均有较大影响，尤其是虚数部分。如图9（a）所示，实数部分的主要影响在前面一、二段带隙部分，对于布拉格带隙的影响不大。如图9（b）所示，阻尼和频变效应使得原本有两段明显的衰减区域合并为一段，在低频处的波都会发生衰减，这也就意味着，在200 Hz以内的振动可能都会向下传播到地基；并且布拉格带隙会被拓宽，衰减程度也会增加。综合来看，不考虑阻尼和频变实频散，会低估轨道结构的实际带隙宽度。

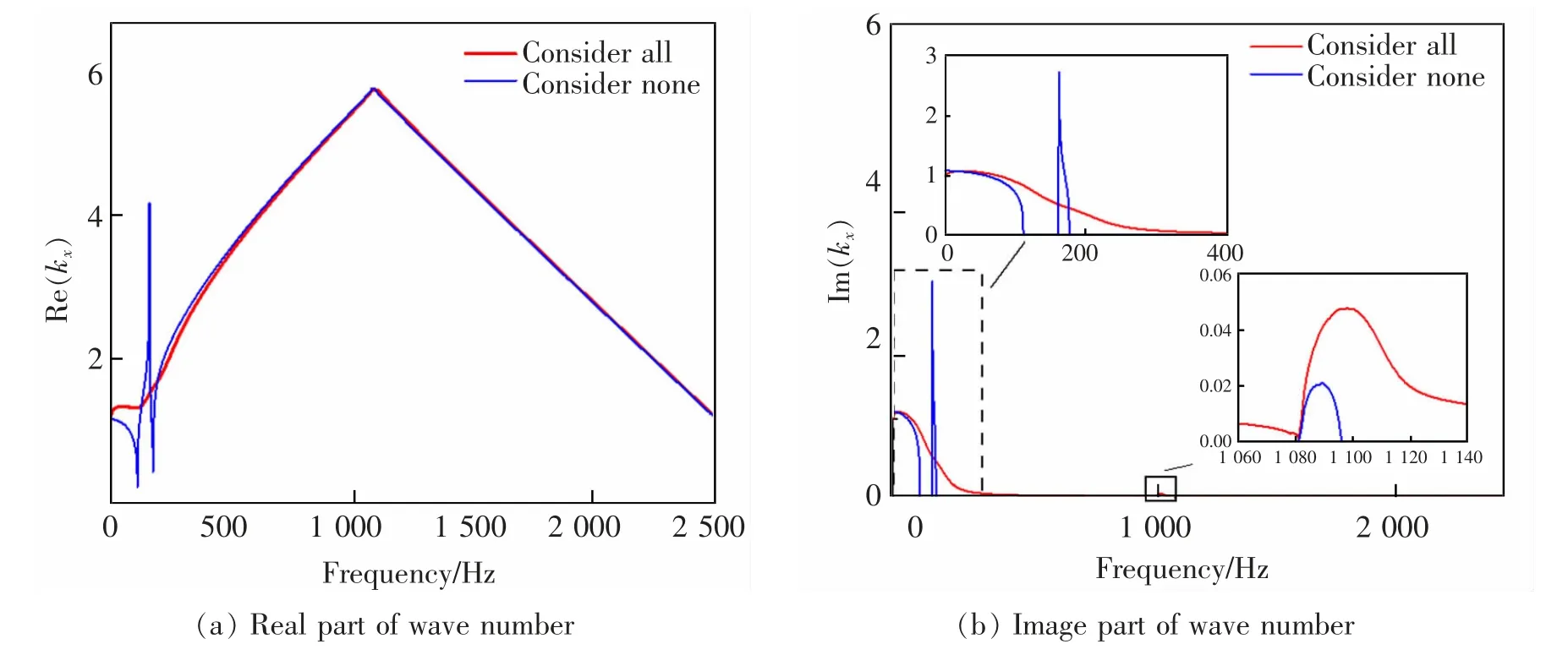
图9 综合考虑下的有砟轨道复频散曲线图Fig.9 Ballasted track dispersion curves considering damping and frequency change effects

4 结论

1）扣件刚度的频变效应对带隙的带宽与衰减能力影响较大，在计算中需要考虑在内，不应忽略。其中布拉格散射产生的带隙对刚度的变化尤为敏感。

2）有砟轨道结构的扣件阻尼和道砟阻尼均会使无阻尼状况时的通带产生衰减，虽会降低局域共振带隙的最大衰减，但增大了衰减域，总体上增加了轨道结构衰减能力。这两者阻尼对布拉格带隙的影响不大。

3）综合考虑频变效应和阻尼对复频散的实部虚部均会产生较大影响，且不考虑任何效应会导致实际带隙被低估。