含时滞的半主动悬架系统稳定性时频分析

王策 罗晓亮 张洋瑞

（重庆交通大学，机电与车辆工程学院，重庆 400074）

1 前言

汽车悬架的作用是减少车辆行驶时的冲击，然而，悬架的阻尼器在响应上存在时滞，可能导致悬架系统失稳，出现危及车辆行驶安全的分岔现象，严重影响车辆的乘坐舒适性。因此，合理的时滞设计可以提高车辆的稳定性。

对于悬架系统的时滞稳定性分析，学者们开展了大量研究。汪若尘等[1]基于多项式判别理论，研究了含时滞的半主动悬架系统的失稳机理，得到了悬架系统的失稳条件和临界时滞，为半主动悬架系统的时滞控制研究提供了基础。邵素娟等[2]运用广义施图姆（Sturm）准则推导了时滞无关稳定区域的临界增益和稳定性开关的临界时滞。庞辉等[3]基于时滞开关天棚控制的半主动悬架模型和时滞微分方程理论，提出了利用李雅普诺夫稳定性理论求解悬架控制系统临界时滞的理论分析和数值计算方法，结果表明，当时滞达到临界值时，悬架系统的稳定性将严重恶化。闫光辉等[4]利用劳斯-赫尔维茨（Routh-Hurwitz）稳定性准则分析了模型的稳定性条件，并计算了系统的临界时滞，计算分析和仿真结果表明，Routh-Hurwitz稳定性准则可以为主动悬架的设计和滞后不稳定机制奠定理论基础。Chu等[5]研究了时滞对受控质量阻尼单自由度系统稳定性的影响和修正问题，求解了导致系统失稳的临界时滞的显式解和数值解。Yan等[6]基于稳定性切换理论，推导了含时滞的主动悬架系统稳定性条件，并通过状态变换和优化方法设计了最优控制策略，仿真结果表明，该策略下悬架系统保持稳定，性能得到改善。

上述研究中时滞方程理论繁琐复杂，难以理解，需简化处理，且未针对特定工况讨论不同时滞的影响，未确定稳定条件下的较优时滞。由于含时滞的1/4半主动悬架系统的特征方程较为复杂，本文将利用滞后理论的全时滞稳定代数判据和稳定性临界点分析半主动悬架系统的稳定性，得到系统全时滞稳定条件和稳定性临界点，通过数值仿真，在特定工况下讨论时滞对系统的影响，并通过时频分析，研究不同时滞点在不同频段对悬架系统稳定性的影响。

2 含时滞的半主动悬架建模

车身的垂向振动主要影响车辆行驶的平顺性，而车辆的结构又相当复杂，本文忽略系统的车身俯仰运动和侧倾运动，建立如图1 所示的含时滞的1/4半主动悬架模型[7]。其中，m1、m2分别为簧上质量、簧下质量，k2、c2分别为悬架系统的刚度和减振器基值阻尼，k1为轮胎刚度，z2、z1分别为簧上质量和簧下质量的位移，q为路面输入，τ为时滞，F(t-τ)为减振器的时滞阻尼力（主要为响应时滞产生的阻尼力）。

图1 含时滞的1/4半主动悬架模型

悬架减振器的阻尼可分为基值阻尼c2和可调节阻尼cτ。考虑到半主动悬架是较为复杂的系统，存在许多时间上的滞后，例如，由作动器引起的响应时间滞后、测量信号在传输上的传输时间滞后和单片机的计算时间滞后均可能影响系统的稳定性。然而，与响应时间滞后相比，计算时间滞后和传输时间滞后非常小，对系统的影响较小，因此本文主要研究减振器内部特性的响应时间滞后对系统稳定性的影响[8]。

含时滞的1/4半主动悬架模型的动力学方程为：

3 时滞稳定条件下可调阻尼和临界时滞的求解

3.1 时滞系统稳定条件下可调阻尼cτ求解

根据时滞微分方程理论，悬架系统的微分方程通解的形式为：

式中，Zi(s)为zi(t)经过拉氏变换的解；s为特征值；t为时间。

将式（2）带入式（1）得到特征方程：

即

要使含有时滞的系统稳定，特征方程D(s,τ)=0需满足以下条件[9]：

a.特征方程D(s,τ)=0的解皆有负实部；

b.特征方程D(s,τ)≠0恒成立。

在条件a下，当τ=0时，特征方程为：

对于条件a，式（5）的所有解均有负实部。然而，在实际悬架系统中，系统的各参数均不可能为负数，因此式（5）各项的系数均大于0。当s=0 时，D(0,0)=k1k2，显然恒大于0；方程的最高次项的幂为偶数，因此，不论s趋于∞或-∞，方程D(s,0)＞0 恒成立，所以，对∀s∈[0,+∞)，式（5）中各项的系数均为正，方程D(s,0)＞0。根据劳斯（Routh）判据判断系统稳定性的充要条件：特征方程所有项的系数均为正数，且Routh 表中第1 列数均大于0，如表1 所示；式（5）的系数满足表1所示的关系。

表1 条件a的Routh判据表

表1中a0、b0、c0、d0可表示为：

因此，满足条件a的公式为：

根据式（6）和式（7）可以求解出满足条件的可调阻尼cτ的取值范围。簧上质量m2、簧下质量m1、轮胎刚度k1、悬架弹簧刚度k2、减振器基值阻尼c2、减振器可调阻尼cτ均为正值，故式（7）恒成立，可调阻尼cτ皆满足条件a。

对于条件b，要使特征方程D(s,τ)≠0 恒成立，令s=iy，且∀y∈R1及∀τ∈R1+，则特征方程D(s,τ)≠0 恒成立等价于D(iy,τ)≠0恒成立，y为不等于0的实数，z为实数，可利用分线式映照处理方程中含时滞的指数项[9]：

集合{ω=eiθ,θ∈[0,2π]}与{z=iy,y∈R}之间构成一一对应关系，式（4）可表示为：

将式（9）中的实部和虚部分开，实部用f(z,y)表示，虚部用g(z,y)表示：

根据式（10）可以求解其结式R(f,g)：

令

则

根据M(y)=0 无实根即等价于条件b 的解，可求解出稳定条件下可调阻尼cτ的取值范围。

综合条件a 和条件b 可求解可调阻尼cτ的取值范围。

3.2 时滞临界点的求解

时滞位移反馈控制会扰动悬架系统。为保证系统的稳定性，本文采用特征根和稳定临界点的方法分析时滞系统的稳定性。时滞独立稳定区是根据悬架系统参数确定的，系统的稳定性不受时滞的影响。

含单个时滞的常系数时滞微分系统的特征方程具有以下一般形式[10]：

其中，PT(s)的次数较QT(s)高，时滞τ≥0，结合式（4）可得到多项式PT(s)和QT(s)：

由时滞稳定性理论可知，时滞系统渐近稳定的充分条件是特征方程的特征解均含负实部。当特征根包含纯虚数时，系统处于稳定与不稳定的边界。假设特征方程存在虚根s=±iω(ω＞0)到达虚轴时，才可能发生稳定性切换，稳定性切换点应满足D(iω,τ)=0，用欧拉公式e-iω=cos(ωτ)-i·sin(ωτ)，则式（15）可表示为[11]：

其中：

为了使D(iω,τ)=0，必须将多项式中的实部与虚部分离。由于式（18）的实部和虚部均为0，可得到：

根据sin2(ωτ)+cos2(ωτ)=1，消除三角函数项，得到关于ω的多项式方程F(ω)：

式中，n为多项式的项数。

根据式（19）可得：

综上所述，D(iω,τ)=0即可等价于F(ω)=0。

系统稳定性切换点在时滞无关稳定性区域外时，系统稳定性是不固定的。特征根的实部会随着时滞的增加而改变符号，这意味着会通过改变时滞来改变系统的稳定性。假设方程实根ω为正，则ω下的一系列临界时滞可由式（23）求解：

其中，θ=ωτ，θ的取值可由式（23）、式（19）求解，取值范围为[0,2π]，因此，一系列的临界时滞点为[12]：

得到临界时滞点后，需要判断每个临界时滞点对应的特征根实部的变化，从而判断系统稳定性的变化情况。式（18）可以视为s对τ的函数，通过求导可得到特征根实部对临界时滞点的变化趋势，由T表示：

由式（15）可得：

从而得到：

式中[13]：

根据式（21）可得：

因此：

从方程F(ω)=0中解得的简单正根为：

相应地得到一系列的临界时滞点τi,k(i=1,2,…,m;k=0,1,2,…)，且有：

由于多项式F(ω)的第1项的系数大于0，有：

和

特征根实部的变化可以由式（25）确定：T=1 表示随着时滞τ的增加，特征根s的实部在复平面内由左向右穿过虚轴，系统从稳定切换到不稳定；T=-1表示随着时滞τ的增加，特征根s的实部由右向左穿过虚轴，系统从不稳定切换到稳定。如果方程没有正的实根，则系统不进行稳定性切换，即无论τ如何取值，系统都是稳定的。如果方程有正的实根，则系统将进行有限次的稳定性切换，最终变得不稳定。因此，利用正实根数量的变化，可以求解系统的临界时滞。

4 时频分析

仿真工况设置为以10 km/h 的车速过减速带，通过分析时频特性研究时滞对系统的影响。表2所示为悬架各参数取值。

表2 悬架各参数取值

根据表2和前文的求解，取可调阻尼cτ=800 N·s/m，分别比较时滞为0 s、0.4 s、0.8 s、1.2 s 条件下过减速带时悬架性能指标的变化情况，分析时滞在不同工况下对系统的影响。

若可调阻尼cτ不在时滞稳定调节范围内，取可调阻尼cτ=1 300 N·s/m，此时悬架各参数不满足时滞稳定条件，根据式（22）求解得到仅有的4 组正实根 分 别 为ω1=7.415 6、ω2=9.338 4、ω3=74.163 1、ω4=95.380 42。

当ω1=7.415 6时，临界时滞点为：

当ω2=9.338 4时，临界时滞点为：

当ω3=74.163 1时，临界时滞点为：

当ω4=95.380 42时，临界时滞点为：

经求解对比，得到系统的稳定临界时滞点为τ=0.025s，因此，稳定性区间为0～0.025 s。在τ=0.025 s附近分别取τ=0.024 s和τ=0.026 s，观察稳定临界点与附近点悬架系统的稳定性和性能指标的变化情况。

本文采用过减速带时轮胎受到的激励为车辆过离散路面的冲击激励，路面减速带模型如图2 所示。为方便分析，将激励模型用三角函数表征[14-15]。

图2 减速带激励模型

减速带激励的数学模型表示为：

式中，h、L分别为减速带的高度和宽度；v为车辆行驶的速度；f为减速带的激励频率；ωr为减速带激励函数。

在时滞稳定条件下，选取不同时滞，在稳态条件下进行仿真，结果如图3 所示。由图3 可知，时滞为0 s、0.4 s、0.8 s、1.2 s 时，系统均处于稳定状态，没有发散现象。时滞为0 s 时，相对于其余时滞，悬架性能指标的第一峰恶化，但通过减速带后，余颤收敛快；表3 所示为时滞稳定条件下不同时滞对应的悬架性能指标均方根，结合表3分析，簧载质量加速度均方根在时滞为0.8 s 时最小，悬架动行程和轮胎动载荷的均方根在时滞为0 s时最小。因此，在离散冲击路面下合理选取时滞，可以提高车辆行驶的平顺性和操纵稳定性。

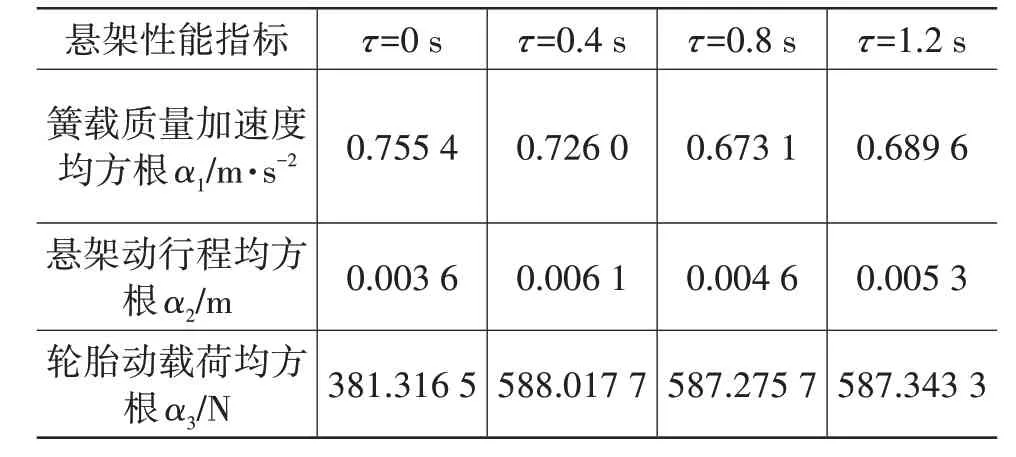
表3 时滞稳定条件下不同时滞对应的悬架性能指标均方根

图3 时滞稳定条件下悬架性能指标时域响应

图4所示为时滞非稳定条件下悬架性能指标时域响应，从图4 中明显可以看出，时滞为0.024 s 和0.025 s 时，在通过减速带后，簧载质量加速度、悬架动行程、轮胎动载荷存在明显的收敛趋势，且时滞为0.024 s时的收敛速度比0.025 s时的收敛速度快，更加稳定，当时滞为0.026 s 时，系统明显发散，处于失稳状态；表4 所示为临界时滞点及附近点悬架性能指标均方根，由表4 可知，在时滞为0.025 s 时，悬架性能指标均方根相对于时滞为0.024 s 时的悬架性能指标数值增大，但不会呈倍数增长，而达到失稳时滞0.026 s 时，悬架性能指标呈倍数增长，造成对系统不利影响。

表4 临界时滞点及附近点悬架性能指标均方根

图4 时滞非稳定条件下悬架性能指标时域响应

图5～图7所示为时滞非稳定条件下的悬架性能指标时频图，由图5～图7 可知，在通过减速带后，时滞为0.024 s和0.025 s时，簧载质量加速度、轮胎动载荷、悬架动行程在各频段下的功率随时间的变化而逐渐减小，且在0～20 Hz频段内的功率明显大于其他频段的功率，随着时滞的增加，其他频段的功率略有增加；时滞为0.026 s 时，簧载质量加速度、轮胎动载荷、悬架动行程在各频段下功率会随时间的变化而逐渐增大，且在0～20 Hz频段下的功率远大于其他频段的功率，相对于时滞为0.024 s和0.025 s，其他频段的功率也明显增加。功率的持续增加，会给车辆造成不利影响，严重影响车辆的行驶安全性。

图5 不同时滞下簧载质量加速度时频图

图6 不同时滞下悬架动行程时频图

综上所述，在离散冲击路面下，时滞为0.024 s和0.025 s时，系统均不会失去稳定性，时滞为0.026 s时，系统发散，明显失稳，降低了行驶安全性，且0～20 Hz 频段的功率明显大于其他频段的功率。时滞稳定时，不同时滞下的悬架性能指标均方根不尽相同。因此，合理选择时滞，可以提高车辆的平顺性和行驶稳定性。

5 结束语

本文通过建立含时滞的1/4 半主动悬架系统，利用时滞微分方程理论，通过分析全时滞稳定性的充要条件，求解可调阻尼cτ的稳定区间范围，对系统特征方程进行分析变换，求解临界时滞点，通过求解得到可调阻尼cτ的稳定区间以及时滞临界点，代入模型进行仿真，在离散冲击路面的条件下，得到以下结论：

a.时域上，当可调阻尼cτ在稳定区间内时，不同时滞下的悬架性能指标不同，但系统均稳定，因此，合理选取时滞有利于提高车辆平顺性和操纵稳定性。当可调阻尼cτ在稳定区间外时，求解得到临界时滞为0.025 s：当时滞为临界时滞和小于临界时滞时，系统仍保持稳定，且时滞小于临界时滞时的悬架性能指标均方根小于时滞为临界时滞时的数据；当时滞大于临界时滞时，系统发散失稳，车辆的平顺性和操纵稳定性恶化。

b.频域上，通过对临界时滞点附近的悬架性能指标进行时频分析可以发现，随着时滞的增加，悬架性能指标的功率逐渐增大，这一情况与时域分析结果相符，并且低频段功率明显大于其他频段功率，功率的持续增加，会给车辆造成不利影响，严重影响车辆的行驶安全性。