基于平方根容积卡尔曼滤波的路面附着系数估计*

杜若飞 王健 李楠 费明哲 邓欢 王云靖

（1.山东交通学院，济南 250357；2.宁波市鄞州德来特技术有限公司，宁波 315100）

1 前言

汽车主动安全系统起到预防车辆发生事故、保护车内乘员免受伤害的作用[1]。路面附着系数是主动安全系统的一个关键参数[2]，直接反映轮胎与路面间的附着情况，因此，准确估计路面附着系数对提升汽车行驶安全性具有重要意义。

路面附着系数的估计方法包括基于结果的（Effect-based）方法和基于原因的（Cause-based）方法[3]。基于结果的方法通过分析由路面变化引起的车辆动力学响应来计算路面附着系数，优势在于不需要额外的传感器，可有效降低成本[4]。基于原因的方法通过测量对路面附着系数影响较大的因素，并依靠经验模型估计路面附着系数，虽然该方法实时性较好，但需要加装额外的传感器，且传感器成本较高，限制了其商业使用[5]，且该方法依赖大量精确的试验数据，对于未知的路面很难精确估计[6]。基于结果的方法主要分为2 种，即基于轮胎响应的方法[7-8]和基于车辆动力学响应的方法[9-12]。前者能够保证检测的实时性，但受外界影响较大；后者可以直接利用车辆自身传感器，成本较低，但易受模型准确度的影响。武钟财[13]利用扩展卡尔曼滤波（Extended Kalman Filter，EKF）算法对车辆状态参数和路面附着系数进行估计，取得了较好的估计效果。王少帅[14]等利用无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法实现了路面附着系数的有效估计。李刚[15]等利用容积卡尔曼滤波（Cubature Kalman Filter，CKF）算法对车辆状态参数和路面附着系数进行估计，并利用驾驶模拟器在环试验对算法进行验证。EKF 算法通过泰勒展开将非线性系统进行局部线性化后转变为线性系统，从而实现良好的估计效果，但会产生较大的截断误差；UKF 算法通过无迹变换产生Sigma 点逼近状态分布，避免了EKF 算法的高阶截断误差；CKF 算法估计精度较EKF 和UKF 算法高，其通过三阶球面-径向容积准则选择容积（Cubature）点，但无法保证协方差矩阵的正定性及观测器的稳定性。

综上，本文针对容积卡尔曼滤波算法在路面附着系数估计中的缺陷，提出平方根容积卡尔曼滤波（Square root Cubature Kalman Filter，SCKF）算法，该方法借助正交三角分解避免CKF 中由协方差矩阵开方造成的矩阵非负定及观测器不稳定问题，可提高估计精度和鲁棒性。基于上述特性，本文在MATLAB/Simulink 中建立三自由度车辆动力学模型与Dugoff 轮胎模型，在CarSim 中建立车辆运行环境，通过SCKF算法估计路面附着系数，利用CarSim/Simulink联合仿真验证算法的有效性。

2 车辆与轮胎建模

2.1 整车模型

车辆动力学模型表示车辆运动过程中各参数之间的函数关系，是设计估计算法的基础，考虑到估计算法的实时性和车辆纵向、侧向及横摆3 个方向的运动，本文采用三自由度车辆动力学模型，如图1所示，并进行如下假设：车辆坐标系的原点与车辆的质心重合；忽略车辆行驶过程中受到的空气阻力与滚动阻力；4 个轮胎力学特性一致；忽略悬架的作用，车身与底盘刚性连接；忽略车辆的侧倾与横摆运动。

图1 三自由度车辆动力学模型

车辆的纵向运动方程为：

式中，m为整车质量；ax为车辆纵向加速度；δ为前轮转角；Fxfl、Fxfr、Fxrl、Fxrr分别为左前轮、右前轮、左后轮、右后轮的纵向力；Fyfl、Fyfr分别为左前轮、右前轮的侧向力。

车辆的侧向运动方程为：

式中，ay为车辆侧向加速度；Fyrl、Fyrr分别为左后轮、右后轮的侧向力。

车辆绕z轴运动时，有：

式中，J为车辆绕z轴的转动惯量；ω为横摆角速度；Mz为回正力矩：

式中，Lf、Lr分别为质心与前轴、后轴的距离；Bf、Br分别为前、后轮距。

2.2 轮胎模型

目前应用较多的轮胎模型有魔术公式（Magic Formula，MF）轮胎模型和Dugoff 轮胎模型，与魔术公式轮胎模型相比，Dugoff 轮胎模型具有参数少和计算量小的优点，考虑到算法的实时性要求，本文采用Dugoff轮胎模型[16-17]计算轮胎受力情况，轮胎受力分析如图2所示。

图2 Dugoff轮胎模型

轮胎的纵向力与侧向力表达式分别为：

其中：

式中，i=f,r 分别表示前、后轮；j=l,r 分别表示左、右轮；μij为各车轮的路面附着系数；Cxij、Cyij分别为各车轮轮胎纵向刚度、侧偏刚度；sij为各车轮轮胎滑移率；αij为各车轮轮胎侧偏角；ε为速度影响因子；vx为车辆纵向速度；Fzij为各车轮轮胎的垂向载荷；分别为各车轮归一化后的轮胎力，忽略了路面附着系数的影响，有利于算法编程；f(L)为模型修正系数；L为轮胎滑移特性参数。

滑移率的计算公式为：

式中，vij为各车轮的纵向速度；ωij为各车轮的角速度；R为车轮有效滚动半径。

车轮中心速度的计算公式为：

式中，vcfl、vcfr、vcrl、vcrr分别为左前轮、右前轮、左后轮、右后轮中心处的速度；ωfl、ωfr、ωrl、ωrr分别为左前轮、右前轮、左后轮、右后轮的角速度；vy为车辆侧向速度。

轮胎侧偏角的计算公式为：

车轮垂向载荷的计算公式为：

式中，La=Lf+Lr为轴距；hg为质心高度。

3 基于平方根容积卡尔曼滤波的路面附着系数估计算法

3.1 平方根容积卡尔曼滤波算法

根据车辆动力学方程式（1）～式（4）确定系统的参数变量为x=[μfl,μfr,μrl,μrr]T，定义系统的观测量为y=[ax,ay,ω]T、系统的输入量为u=[δ,F0xij,F0yij]T，具体估计过程为：

a.对于一般的非线性系统，其状态空间方程可以写成：

式中，f(x(t),u(t))、h(x(t),u(t))分别为估计系统的状态方程和量测方程；w(t)为过程噪声；v(t)为量测噪声。

估计器的状态方程和观测方程可以表示为：

b.采用奇异值分解（Singular Value Decomposition，SVD）方法对状态量误差协方差矩阵进行分解：

式中，Gk-1|k-1为状态误差协方差矩阵；Pk-1|k-1为(k-1)时刻状态量误差协方差矩阵；svd()为矩阵分解函数。

c.计算容积点：

式中，；xk-1为(k-1)时刻状态量的预测值；n为状态量的维度为容积点权重矩阵；B=[In×n-In×n]。

d. 计算经过状态方程迭代后的容积点及预测的状态量：

其中：

式中，xk|k-1为k时刻的状态预测值。

e. 计算状态量预测值的误差协方差矩阵的平方根：

f.计算更新容积点：

g.将容积点代入量测方程进行传播：

式中，yk|k-1为k时刻观测量估计值。

h. 计算观测量预测值的误差协方差矩阵的平方根：

i.计算互协方差矩阵：

k. 更新状态量得到路面附着系数最优估计值：

l.更新误差协方差矩阵的平方根因子：

3.2 路面附着系数估计模型

为验证本文提出算法的有效性，利用CarSim 与Simulink 联合仿真平台进行验证。首先，在CarSim中搭建整车运行仿真工况，设定输入、输出参数；然后，在Simulink 中搭建三自由度车辆动力学模型、Dugoff 轮胎模型和算法模块；最后，进行CarSim 与Simulink 联合仿真，通过设置不同的路面仿真工况，对SCKF 和CKF 算法在路面附着系数估计方面的准确性和鲁棒性进行对比分析，模型整体框图如图3所示。

图3 路面附着系数估计框架

4 仿真验证

为验证SCKF 观测器的有效性和鲁棒性，设计了制动工况下的低附着系数路面、高附着系数路面及对接路面工况进行对比验证，并对CKF 算法和SCKF 算法进行对比分析，仿真模型选用CarSim 中自带的车辆模型，相关参数如表1所示。

4.1 低附着系数路面仿真验证

在CarSim中设置车辆初始速度为80 km/h、节气门开度为0、挡位为空挡、轮缸压力为0.45 MPa，路面附着系数设置为µ=0.4，仿真时间为10 s，仿真结果如图4所示。对比仿真曲线可知，CKF算法和SCKF算法均有向标准值收敛的趋势，相较于CKF算法，SCKF算法收敛精度更高。这是由于SCKF算法利用正交三角分解法保证了协方差矩阵的正定性，而CKF算法利用平方根分解导致了协方差矩阵负定。在车辆前轮路面附着系数估计中，CKF的估计误差在10%以内，SCKF的估计误差在3%以内；在车辆后轮路面附着系数估计中，2种算法的估计误差稍大，但SCKF算法的估计误差仍低于CKF算法的估计误差。

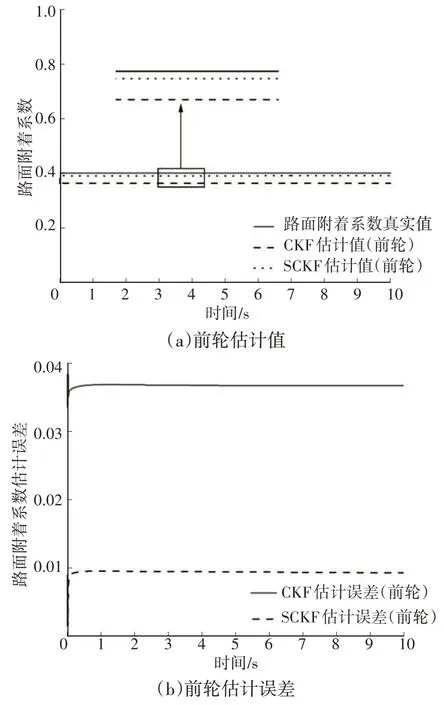
图4 低附路面下附着系数估计结果对比

4.2 高附着系数路面仿真验证

保持CarSim 中其他参数不变，只改变路面附着系数，设置路面附着系数µ=0.85，继续进行仿真验证。验证结果如图5 所示，与低附着系数路面情况大致相同，CKF算法的最大估计误差为12.8%，SCKF算法的最大估计误差为3.62%。

图5 高附路面下附着系数估计结果对比

4.3 对接路面仿真验证

设计对接路面工况，在CarSim 中设置路面附着系数在100 m 处（约第4.9 s）从0.85 突变到0.20，其他参数保持不变，仿真结果如图6 所示。在路面附着系数发生突变时，SCKF 算法可以快速响应路面附着系数的变化，误差曲线抖动较小，最大误差仅为0.041 9，而CKF 算法不能快速响应路面的变化，最大误差为0.728 6，这是由于在路面附着系数发生突变时，SCKF 算法利用正交三角分解法保证了协方差矩阵的正定性，而CKF 算法使用的平方根分解法计算量较大且容易造成协方差矩阵负定，导致估计结果与真实值偏差较大。

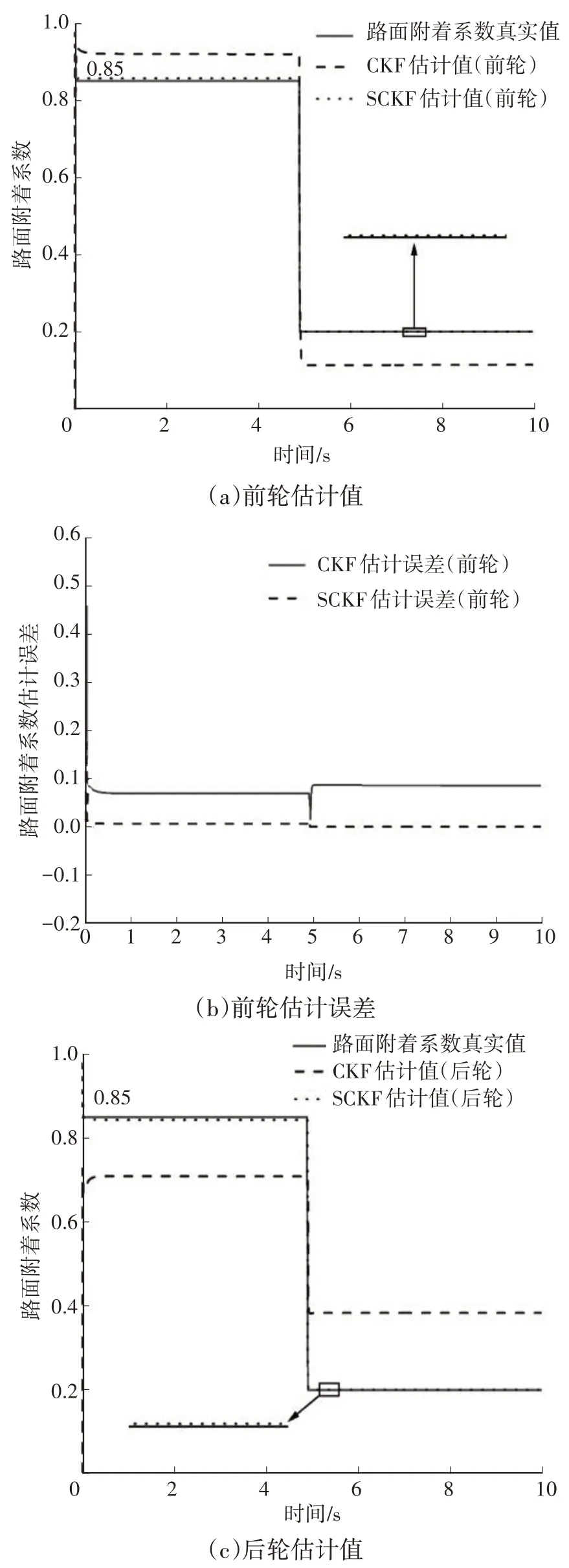
图6 对接路面下附着系数估计结果对比

5 结束语

本文在传统的容积卡尔曼滤波算法基础上针对协方差矩阵不对称或非负定导致的滤波发散及观测值不稳定的问题进行改进，提出了平方根容积卡尔曼滤波算法。利用CarSim 与Simulink 进行联合仿真，验证了改进算法的有效性。得到以下结论：

a.以三自由度车辆动力学模型为基础，可通过平方根容积卡尔曼滤波算法估计路面附着系数；

b. 采用正交三角分解法可以克服传统容积卡尔曼滤波算法中协方差矩阵不对称或非负定导致的滤波发散及观测值不稳定的问题；

c.平方根容积卡尔曼滤波算法鲁棒性强，可在多种路面附着条件下进行路面附着系数估算。

本文仅在不同路面附着系数条件下开展了仿真验证，未开展驱动、转向等工况下的仿真验证，未来将继续使用平方根容积卡尔曼滤波算法在驱动、转向以及制动等联合工况下开展关于路面附着系数估计的研究，为车辆主动安全系统的设计提供参考。