考虑燃油消耗量的自动驾驶汽车交叉路口生态驾驶行为决策研究

李佳丽

（重庆交通大学，重庆 400074）

1 前言

信号交叉路口是交通路网中的瓶颈区域，车辆在遇到红灯时被迫停车，从而在车流中产生停车冲击波，导致车辆的燃料消耗量和污染物排放量增加，而不必要的怠速也会导致额外的燃油消耗和尾气排放[1-2]。目前，针对交叉路口的生态驾驶研究主要集中于车辆的加速度控制策略。Homahaudhuri 等[3]建立匀加速-匀速车辆模型，求解出车辆通过交叉路口的最优车速。Kamalanathsharma 等[4]提出三角函数加速度模型，车辆在执行加速和减速操作时，分别根据三角函数曲线选取相应的加速度，根据瞬时车速引导车辆不停车通过路口。以上基于规则的控制方法是采用预定规则计算车辆通过一个或者多个交叉路口、避免停车的建议车速，而没有直接给出速度轨迹与燃油消耗量的关系。

在交叉路口驾驶行为决策研究方面：杜明博[5]针对影响行为决策的因素种类繁多的问题，利用灰色关联法分析各影响因素的主次关系，并构建了基于ID3决策树的驾驶行为决策模型；邢岩[6]针对交叉路口处交通环境存在不同复杂程度使驾驶员行为判别模型准确度低的问题，建立基于模糊聚类理论的复杂交通场景下驾驶员行为决策模型，在交通影响因素稳定时采用贝叶斯概率方法构建驾驶员行为决策模型；陈永尚[7]针对多目标下的最优驾驶行为选择问题，将交通参与者与交通法规解耦建模，构建基于交通规则的驾驶行为集合，结合隐马尔可夫模型识别周围车辆的驾驶意图，综合各性能指标决策出最优驾驶行为；冀杰[8]等将自动驾驶运动过程分解为车道保持、车辆跟随、车道变换和制动避撞4 种驾驶行为，构建基于有限状态机方法的各驾驶行为间逻辑关系、状态切换过程以及自动驾驶虚拟危险势能场。但上述针对交叉路口驾驶行为决策的研究并未考虑燃油消耗量。

针对以上问题，本文考虑前车对自动驾驶汽车运动的约束，建立自动驾驶汽车交叉路口驾驶行为决策模型。根据决策获得的不同行为，基于车辆燃油消耗量，将多阶段生态驾驶最优控制问题转换为全阶段最优控制问题，提出交叉路口自动驾驶汽车生态驾驶策略，并通过仿真验证其有效性。

2 前车影响下交叉路口自动驾驶决策行为模型

2.1 建模数据预处理

NGSIM 数据会影响后续聚类结果，因此采用数据平滑的方法对数据进行处理。

为提高模型精度，应对原始数据进行滤波处理，可以将采集的实际数据表示为：

式中，Yi为真实值；Δyi为随机误差。

为使测量结果更接近真实值，需要对非平稳的动态数据{yi}进行滤波或者平滑处理。假设{yi}含有的数据样本数量为N，将每次连续测量所得的数据作为一个小区间，对小区间内的每个数据进行局部平均，用均值代替区间中处于最中间位置的实测值，以减小误差对测量值的影响。设n为分区序号，每个分区数据点数量为(m+1)，其中m为偶数，若n=1、m=4，则有S3=(y1+y2+y3+y4+y5)/5，统一表示为[9]：

2.2 基于高斯混合模型-支持向量机的周围车辆驾驶风格辨识

2.2.1 基于高斯混合模型的驾驶风格聚类

高斯混合模型（Gaussian Mixture Model，GMM）的概率密度函数可以表示为：

式中，K为高斯分布的数量；πk、μk、Σk分别为第k个高斯分布的权重、均值、协方差矩阵；ρ(x|μk,Σk)为第k个高斯分布的密度函数。

分布函数在计算待聚类数据点的分布时获得的最大概率为：

式中，xi为待聚类数据点的样本向量。

采用取对数的方法，使得概率求解时的乘积转变为求和运算，则似然函数可表示为：

根据式（5）求极大值所得到的结果即为高斯混合模型需要的最优值，但是由于存在非凸现象，造成该函数只能得到局部极值，通常采用期望最大化（Expectation-Maximization，EM）算法估计GMM 参数[10]。样本数量大使单个数据点聚类时的概率（似然函数）极小，对似然函数取对数，有：

式中，Σ为协方差矩阵；π为每个分量的权重参数。

已知一组样本，假设存在K类，估计合适的参数θk(πk、μk、Σk)，使得样本在该组参数上可以获得最大的概率。EM 算法中每一次迭代均存在期望步（E步）和极大步（M步）：

a.E 步。引入隐变量，表示第i个样本属于第k类的概率：

式中，z为隐含变量；θ为样本参数；p(z=k|xi;θ)为后验概率；φ(xk|θk)为一个高斯分布的概率密度函数。

b.M步。根据γik更新θk(πk,μk,Σk)：

c.不断重复E步和M步，直到模型的参数收敛为止。

本文将驾驶员风格划分为保守型、一般型、激进型[11]，则确定高斯分布模型数量为K=3 个。聚类结果如图1 所示。3 种类型驾驶员呈现明显的聚类分布特点，具有相似的聚类中心，不同类型驾驶员的特征参数反映其驾驶风格。在交叉路口跟车行驶时，加速度分布差距较小，不能准确反映驾驶风格的差异。

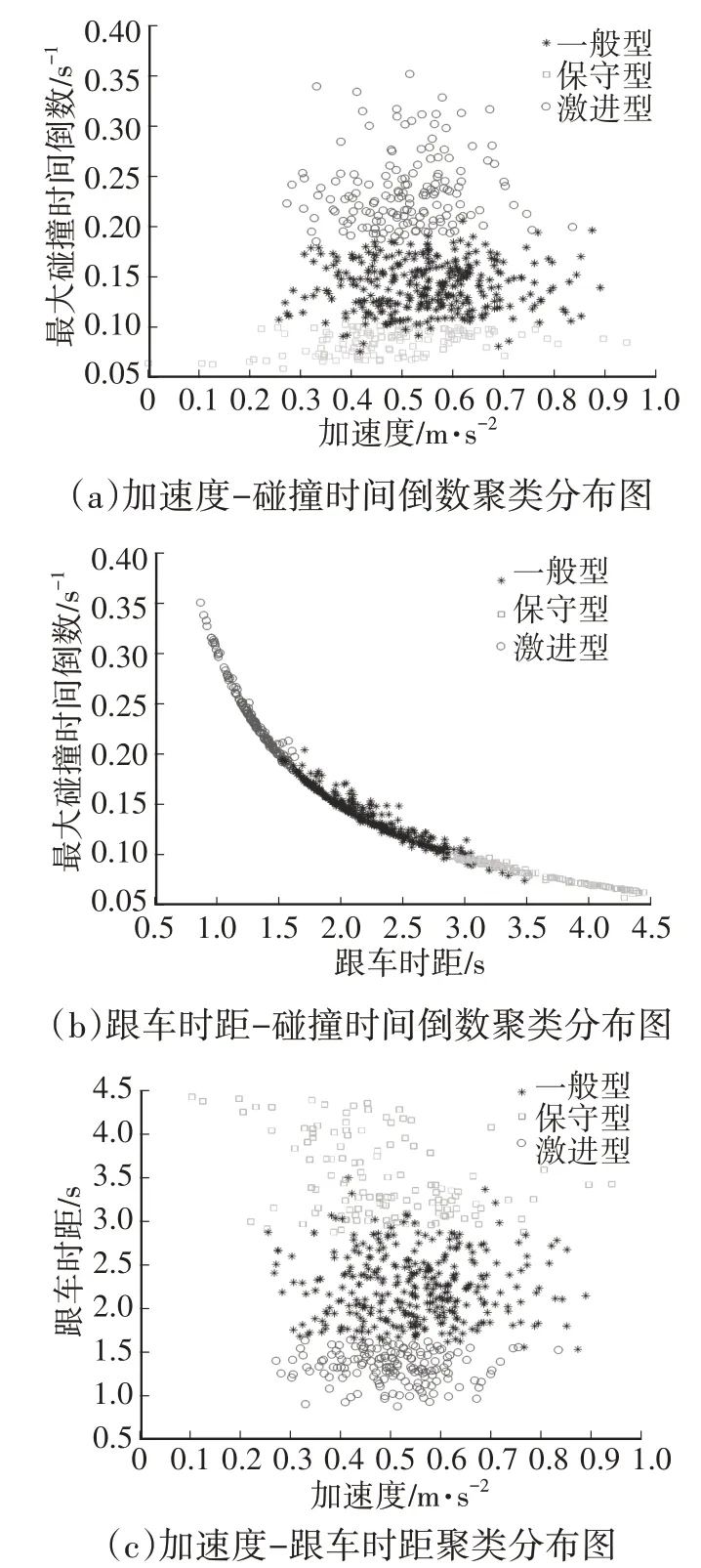
图1 驾驶员行为特性分类结果

2.2.2 基于支持向量机的驾驶员行为特征辨识

针对非线性样本，引入核函数K(xi,yi)，将原始数据中的非线性样本数据一一映射到高维空间，寻找一个多维超平面将样本分开。

将分类问题描述为：

式中，ω、b分别为超平面的法向量和截距；ξi为松弛参数。

对于训练样本集{(x1,y1),(x2,y3),(x3,y4),…,(xl,yl)}，最优超平面问题可转化为二次规划问题：

式中，φ(ω)为优化函数；C为惩罚因子。

引入拉格朗日（Lagrange）函数，求解约束最优化问题：

式中，α、αi、ηi为拉格朗日函数乘子，且αi≥0、ηi≥0。

利用拉格朗日泛函数的对偶性原理，将约束最优化问题转换成对偶二次规划问题。对ω、b、ξi求偏导，令其等于零，可得：

由式（14）、式（15）可得到对偶优化问题：

式中，W(α)为二次规划问题最优解；φT(xi)φ(xj)即为核函数，其决策函数为：

选取不同的核函数，会生成不同的支持向量机（Support Vector Machine，SVM）分类器，训练获得的模型效果也不同，本文采用多项式核函数：

式中，c、d为常数。

在对模型进行训练的过程中，以跟车时的驾驶风格聚类结果为依据，建立了具有400 组驾驶员行为特征数据的训练样本。训练结果中保守型驾驶员、一般型驾驶员、激进型驾驶员分别对应驾驶员类型1～3。完成模型训练后，将聚类结果剩余的241组数据导入辨识模型进行测试，SVM 识别结果如表1 和图2 所示，241 组测试数据中，235 组数据被正确识别，正确率为97.51%，为后文决策模型的建立提供了可靠依据。

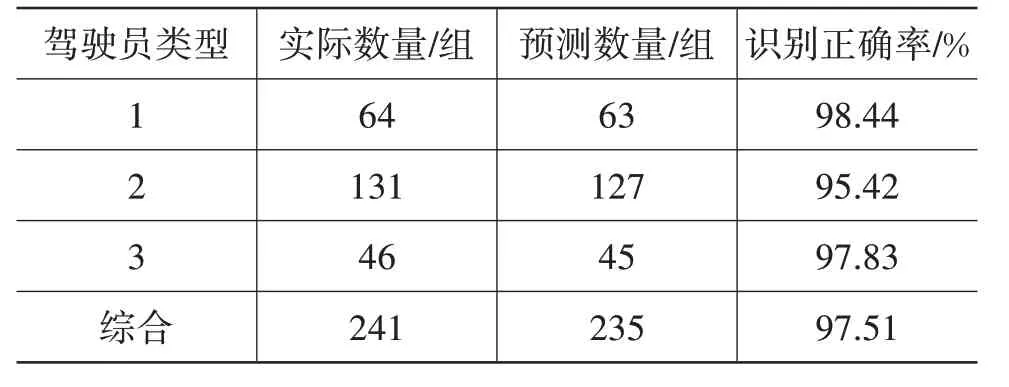
表1 驾驶员类型识别结果

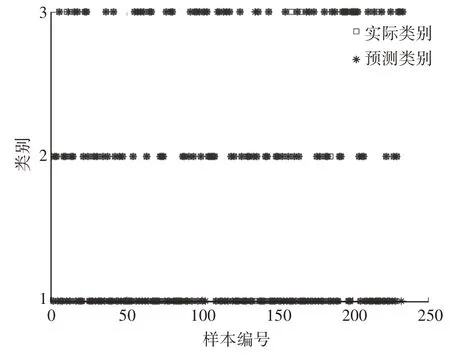
图2 驾驶员行为特性辨识结果

2.3 前车影响下交叉路口自动驾驶行为决策模型

2.3.1 逻辑回归模型结构

逻辑回归（Logistic Regression）属于概率型非线性回归，它是研究二分类观察结果与一些影响因素之间关系的一种多变量分析方法，可以用来研究道路交通信息对驾驶员行为的影响。令回归模型系数β=(β1,β2,…,βk)，k个自变量表示为X=(x1,x2,…,xk)T，则逻辑函数基本形式表示为：

P(Y=1|X)表示当变量为x1、x2、……、xk时，因变量为1 的概率。逻辑回归函数图像为S 型函数（Sigmoid Function）曲线，如图3所示。

图3 S型函数曲线

对式（18）进行对数变换，可以将逻辑回归问题转化为线性回归问题，则有：

式中，β0、β1、……、βi为模型参数。

将车辆越过交叉路口停止线的行为视为通过交叉路口，则车辆在交叉路口的行为可以分为通过和不通过2 种类型。存在前车干扰时，可以将车辆行为分为跟车和不跟车行驶，则在交叉路口，车辆可能跟随通过、跟随停车和自主停车。综上，令车辆在交叉路口跟随前车行驶的概率为P，跟随前车和自主停车完全对立，则自主停车的概率可以表示为(1-P)。交叉路口行为决策二元逻辑回归模型见式（18）。

2.3.2 逻辑回归模型的自变量选取

交叉路口处影响驾驶行为决策的主要因素是信号灯灯态及当前灯态剩余时间，结合车辆的速度和位置、前车速度和位置以及驾驶风格等变量，组成逻辑回归模型的多变量输入，如表2 所示。

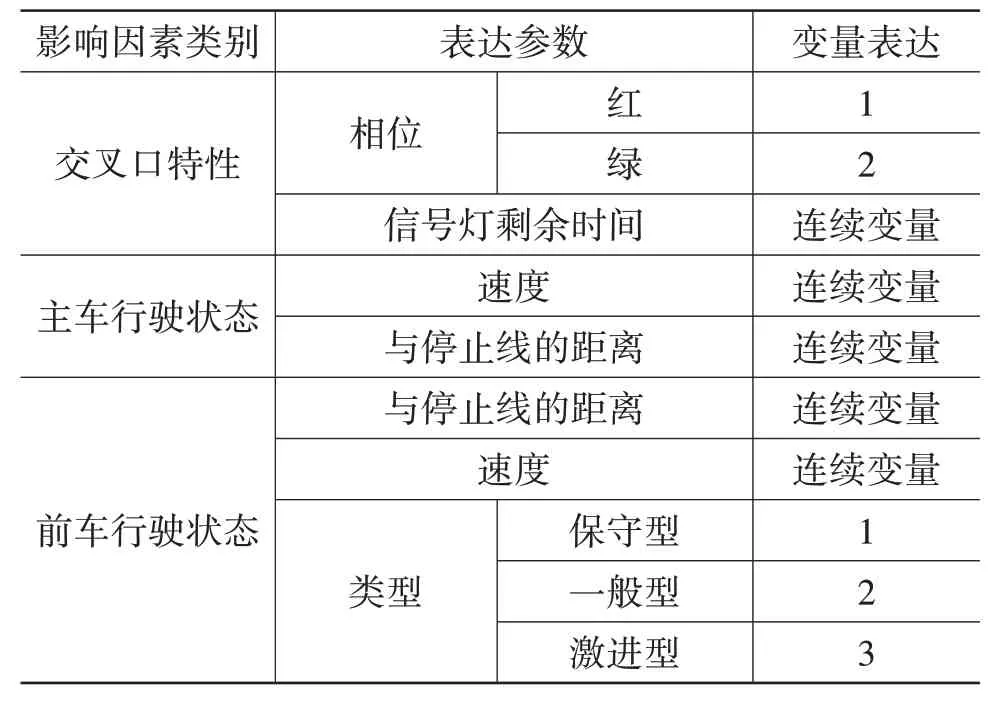
表2 自变量表达

前车驾驶风格分为保守型、一般型、激进型3类，由GMM-SVM 驾驶风格辨识模型获得，分别表示为1、2、3；分别将红、绿灯相位表示为1、2。

2.3.3 计算结果分析

使用SPSS 统计软件进行标定模型参数和显著性检验。在SPSS中，可以通过比较每个自变量的显著性（Sig.）与显著性水平a（通常取a=0.05）来确定自变量与因变量之间的显著性相关程度：Sig.＞a时，表示相关性不显著；当Sig.＜a时，表示相关性显著。建立逻辑回归模型时需要考虑样本量，一般要求样本量为自变量数量的5～10 倍。本文中存在8 个自变量，所以选择80 个样本进行模型训练，参数估计结果如表3 所示。其中，B为回归系数，exp(B)为回归系数B的指数函数，B和exp(B)无量纲。

表3 模型参数及相关性分析

根据模型计算结果，所选变量的显著性均小于0.05，表明它们与因变量之间相关性显著。具体而言，在交叉路口跟车行驶时，信号灯相位、通过时间以及车辆通过行为与因变量之间的相关性最强。驾驶员会根据信号灯当前相位和剩余时间来调整驾驶行为。主车和前车与停止线的距离及主车的速度也影响决策结果，与停止线距离越近，对决策结果的影响越大。此外，前车的驾驶风格和速度也会对决策结果产生影响。

3 考虑燃油消耗量的交叉路口生态驾驶速度决策

根据行为决策模型的输出，通过车路（Vehicle to Infrastructure，V2I）通信获取车辆的位置、速度和信号灯相位与配时（Signal Phase and Timing，SPaT）信息，利用伪谱法计算参考速度序列，使车辆遵循此速度序列行驶时消耗的燃料最少。本文将该生态驾驶问题表述为最优控制问题（Optimal Control Problem，OCP），利用伪谱法将最优控制问题转化为非线性规划（Nonlinear Programming，NLP）问题求解。

3.1 生态驾驶最优控制问题构建

3.1.1 多阶段速度最优控制问题构建

车辆纵向动力学模型为：

式中，v(t)为控制量；s(t)、v(t)为状态量；m为整车质量；i0、ig分别为主减速器、变速器传动比；η为动力传递效率；r为轮胎半径；T为发动机转矩；CD为空气阻力系数；A为迎风面积；f为路面摩擦因数；ε为道路坡度。瞬时燃油消耗量可以表示为：瞬时燃油消耗量不能用于评估车辆行驶过程中的油耗水平，因此，以单位里程能耗Fc作为经济性评价指标，则Fc重新定义为：

式中，tc、ta、td、te分别为匀速行驶时间、加速行驶时间、减速行驶时间和怠速行驶时间；mfc、mfa、mfd、mfe分别为匀速、加速、减速和怠速过程中的瞬时燃油消耗量；sc、sa、sd分别为匀速行驶距离、加速行驶距离和减速行驶距离。

3.1.1.1 匀速行为

车辆匀速通过路口时，发动机一直处于稳定工况，瞬时燃油消耗量趋于平稳，所以不需要以最小燃油消耗量为目标进行速度优化。

3.1.1.2 加速行为

此工况下的经济性目标函数可由式（22）调整为：

式中，J为目标函数；tf为通过路口需要的时间。

在车辆运动过程中，为保证通行效率和提高燃油经济性，必须满足必要的约束条件，包括运动学约束、状态约束、边界约束。

车辆从加速到匀速状态的转化过程中，多阶段状态应满足：

式中，t0为初始时刻；s0为初始距离；v0为车辆初速度；va为加速结束时速度；sf为以vf通过路口行驶的距离；D为车辆与停止线的距离；vf为匀速通过路口的速度。

为保证行车安全和舒适性，行驶过程中的位置、速度和加速度应满足：

式中，vmin、vmax分别为车辆行驶过程中的最小速度和交叉路口限速；amax为车辆加速时的最大加速度。

运动学约束为：

绿灯相位下，车辆通过加速可以不停车通过路口，则时间约束为：

式中，tg为绿灯剩余时长。

3.1.1.3 减速行为

最小燃油消耗量可表示为：

车辆从减速到匀速状态的转换过程中，多阶段状态应满足：

式中，vd为减速通过交叉路口的最终速度。

为保证行车安全性和舒适性，行驶过程中的位置、速度和加速度应满足：

运动学约束为：

车辆通过减速可以不停车通过路口，则时间约束为：

式中，tr为红灯剩余时长。

3.1.1.4 怠速行为

此时最小燃油消耗量表示为：

车辆从减速到怠速状态的转换过程中，多阶段状态应满足：

为保证行车安全性和舒适性，行驶过程中的位置、速度和加速度应满足：

运动学约束为：

车辆通过减速可以不停车通过路口，则时间约束为：

3.1.2 多阶段最优控制问题转换

通过将问题转换为全阶段的最优控制问题，多阶段的最优控制问题可以得到解决。这样，车辆到达路口停止线时的最低燃油消耗量可以通过全阶段最优控制问题来表示：

动态约束为：

边界约束为：

式中，Te、Temin、Temax分别为通过路口时发动机转矩、最小发动机转矩和最大发动机转矩；amin为车辆加速时的最小加速度；tfmin、tfmax分别为末段时间约束下限和上限，取值与SPaT和工况相关。

联合式（38）～式（40），面向最低燃油消耗量的生态驾驶问题可转换为：在时域[t0,tf]内，受控系统的状态变量从初始状态x0=(s0,v0)T转移到终点状态xf=(sf,vf)T，寻求一个控制矢量U(t)=[u0(t),u1(t),…,uf(t)]，使得性能指标J取得最小值，此时的u(t)便为最优控制u*(t)，在u*(t)作用下的v(t)为最优速度轨迹。

3.2 基于伪谱法的生态驾驶速度最优化求解

3.2.1 时域转化

在进行离散化时，利用高斯-勒让德（Gauss-Legendre）求积公式近似目标函数中的拉格朗日型性能函数，勒让德多项式是在区间[-1,1]上的正交多项式，所以在用高斯-勒让德公式求积时，应进行时域转化，过程为：

其中：

式中，区间[a1,b1]为函数f(t)积分区间a1、b1；τ为求积节点；F(τ)为区间[-1,1]上的两点高斯公式。

3.2.2 拉格朗日多项式

选择拉格朗日基函数用于状态变量的近似。在[-1,1]之间设置(N+1)个离散点，离散后的(N+1)个状态变量表示为X={X0,X1,X2,…,XN}，控制变量为U={U0,U1,U2,…,UN}，则第k个点的状态变量和控制变量可以近似表示为：

式中，τi为离散点。

其中拉格朗日基函数Lk

i(τ)为：

为避免使用拉格朗日基函数插值时出现龙格（Runge）现象，伪谱法采用的零点为正交多项式的零点。设v,g⊂[a,b]，ρ为[a,b]上的权函数，若

则称多项式集合v,g 在区间[a,b]上带权ρ正交，其中v(x)、g(x)为区间[a,b]上两个多项式。在[1,-1]区间，ρ≡1 时的正交多项式为勒让德多项式。本文采用正交配点作为离散点，可随约束条件的增多，瞬态调整网格数量和多项式次数。

3.2.3 状态方程转化

将状态变量转化为对插值基函数的微分求解[12]，则有：

其中，Dki为微分矩阵D（N+1）×（N+1）中的元素，表示各勒让德-高斯-拉道（Legendre-Gauss-Radau，LGR）配点处的微分，数学表达为[13]：

式中，PN(τi)为LGR的N阶多项式。

由此，可将动力学约束转化为：

3.2.4 性能函数与边界约束转化

利用高斯-洛巴托（Gauss-Lobatto）积分方法可以将性能函数中的积分项转化为：

式中，G为被积多项式函数；wi为高斯-洛巴托积分权重。在区间[-1,1]，用状态方程可以将末端状态表示为：

经离散插值后得到的末端状态近似为：

则边界约束离散后可以表示为：

式中，τf为状态变量。

式（53）即为边界约束条件。

3.2.5 非线性规划问题描述

利用伪谱法将连续变化的状态变量和控制变量进行离散、多项式逼近，性能函数和约束条件也经过离散变换，则最优控制问题转化为非线性规划问题，表示为：

式中，C(X(τk),U(τk),τk)为路径约束函数。

伪谱法将连续系统最优控制问题转化为受一系列代数约束的非线性规划问题，采用高斯伪谱优化软件（Gauss Pseudospectral OPtimization Software，GPOPS）工具箱求解，其求解过程如图4所示。

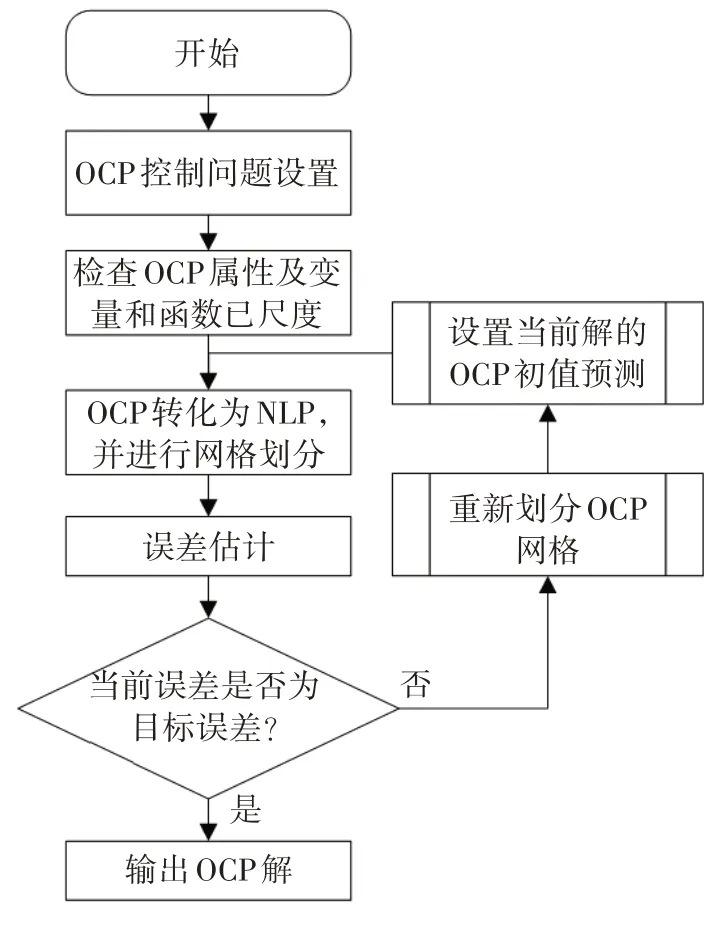
图4 GPOPS求解流程

4 仿真分析

4.1 仿真工况设置

本文基于MATLAB/Simulink平台对生态驾驶策略进行仿真。以车辆进入V2I通信范围的位置作为初始位置，设初始位置与交叉路口停止线的距离为200 m，取交叉路口最高限速vmax、最低限速vmin分别为70 km/h、10 km/h。设置仿真工况如表4所示。

表4 仿真工况

4.2 仿真结果

4.2.1 车辆通过交叉路口

将相位配时信息和车辆初速度40 km/h 输入决策模型，得到结果为车辆可以加速通过路口，采用匀加速策略和生态驾驶策略时车辆的位移、速度、加速度及瞬态燃油消耗量曲线如图5所示。

图5 40 km/h初速度下驾驶策略对比

从图5a中可以看出，在[0.1,15.0]s时间范围内，2 种策略均可使车辆安全通过路口。由图5b、图5c可以看出，在匀加速策略作用下，车辆先以2.2 m/s2加速度匀加速行驶1.1 s，然后以43.5 km/h的速度匀速行驶，生态驾驶策略使车辆先加速后减速通过路口。由图5d可知，瞬态燃油消耗量曲线与坐标轴围成的图形面积为整个过程中的总燃油消耗量，显然，匀加速策略的总燃油消耗量较生态驾驶策略高。采用匀加速策略时的行驶时间为14.7 s，百公里燃油消耗量为9.952 9 L，采用生态驾驶策略时的行驶时间为15.0 s，百公里燃油消耗量为6.245 7 L，燃油消耗量降低了37.24%。

4.2.2 怠速停车

50 km/h、30 km/h 初速度下匀减速停车策略和生态驾驶策略的位移、速度、加速度及瞬态燃油消耗量曲线如图6、图7所示。

图6 50 km/h初速度下驾驶策略对比

图7 30 km/h初速度下驾驶策略对比

由图6a、图7a 可知，车辆驶入V2I 通信区域的初始速度不同，但都能在40 s内到达交叉口停止线，并在路口停车等待，匀速、减速、怠速时间以及百公里燃油消耗量如表5所示。

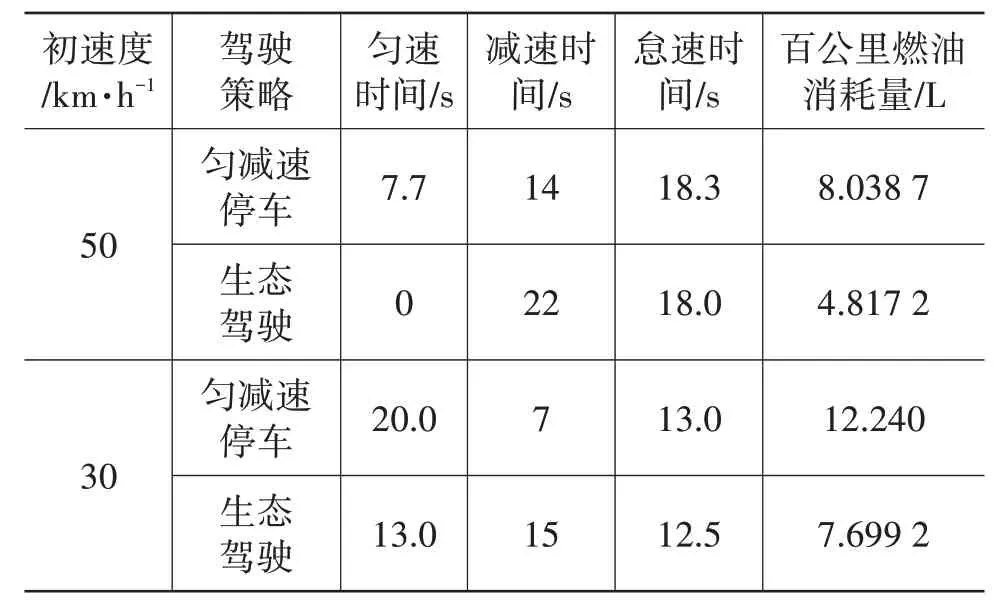
表5 绿灯转红灯情况下驾驶策略对比（怠速停车）

由表5可以看出，随着初速度的降低，匀速行驶的时间逐渐延长，减速时间、怠速时间缩短，燃油消耗量也随之增加，但相对于匀减速停车策略，生态驾驶策略有更长的减速时间，且整个时间范围内的燃油消耗量降低。因此，生态驾驶策略的经济性能优于匀减速策略，更有利于生态驾驶。

综上可知，初速度对燃油经济性有一定的影响，初速度越低，产生的燃油消耗量越高，且车辆匀速行驶时燃油消耗量不一定最低，因为车速高时，行驶阻力较大，使燃油消耗量提高，而低速行驶时，发动机的负荷率较低，发动机有效燃油消耗率较大，导致百公里燃油消耗量增加。但基于伪谱法的生态驾驶策略得到的最优速度曲线对应的转矩可以使发动机工作在高效率区间，燃油经济性较好，有利于生态驾驶。

5 结束语

本文提出了一种考虑燃油消耗量的自动驾驶汽车交叉路口生态驾驶行为决策方法。首先，基于经验型节油策略，提出了在信号灯影响下的车辆生态驾驶行为决策方法。接着，考虑前车驾驶风格对自动驾驶汽车决策行为的影响，通过从NGSIM 中提取的跟车数据集进行驾驶风格聚类分析，构建了基于GMM-SVM 的驾驶风格辨识模型。在考虑驾驶风格、信号配时和两车运动状态的基础上，建立了基于二元逻辑回归的交叉路口驾驶行为决策模型。最后，采用伪谱法解决生态驾驶速度优化问题，以优化交叉路口自动驾驶汽车的驾驶行为决策结果。仿真验证结果表明，本文提出的自动驾驶汽车交叉路口生态驾驶策略在保证行车安全的同时，有效降低了燃油消耗量，有助于实现生态驾驶。