基于CO-需风量理论的隧道施工通风控制优化模型研究
张佳鹏, 郭 春, *
(1. 西南交通大学土木工程学院, 四川 成都 610031; 2. 西南交通大学 交通隧道工程教育部重点实验室, 四川 成都 610031)
0 引言
随着国家交通建设的深度发展,长大隧道日益增多,施工通风系统是保障施工安全的重要部分,其成本也随着隧道长度的增加而增加。目前,压入式通风为最常用的通风方式,其风机设计需满足隧道建设周期内的最大需风量。但在隧道建设过程中,施工环境受到掘进距离、工况等要素的影响,实际需风量往往小于设计风量。实时监测隧道环境有害气体、粉尘、温湿度等要素变化,采用智能控制技术动态调整风机风量以满足施工需求是有效降低施工通风成本的方式之一。
国内外学者主要将智能控制技术的研究重点放在隧道运营期间,如公路隧道运营通风系统[1]、城市地铁环控系统[2]和综合管廊通风系统[3],而在隧道施工通风系统中应用还不成熟。由于隧道运营期间和施工期间二者环境的差异,运营通风系统的智能控制技术无法直接应用于施工通风系统。
隧道施工通风智能控制系统主要是将传感器监测的有害气体、粉尘等要素数据实时传输给PLC进行处理,控制变频器调节风机的交流电频率以改变风机转速,从而达到调节供风量的目的,满足隧道施工需求[4]。有学者对此进行了研究: 余发山等[5]提出一种模糊PID迭代学习算法, 通过把设计控制算法的问题转换成对模糊PID控制器3个参数Kp、Ki、Kd进行整定的问题; 刘石磊等[6]在天目山隧道杭黄铁路闻家斜井采用BP人工神经网络对风机司机的操作过程进行学习,建立了一种基于工业以太网络的隧道施工通风监控系统; 吴燕升[7]在高原铁路某隧道2号斜井采用智能化通风供氧控制系统,施工环境良好,且节能27%; Liu等[8]在西南华蓥山隧道基于径向基函数神经网络设计了关于隧道进尺的隧道通风智能变频控制系统,使能耗降低了42%。
通过以上文献调研可知,目前对隧道施工通风智能控制技术的研究还不完善,主要是提出模糊控制、神经网络控制等控制方法,现场试验只对隧道应用了单一控制方式,没有对不同的控制方法进行对比分析,缺乏对隧道施工建设全周期的通风效果研究。由于CO是隧道施工环境中的主要有害气体,可以代表隧道施工通风中有害气体的运移扩散规律,因此本文选用CO体积分数作为控制指标,建立隧道施工爆破通风和机械出渣下CO-需风量理论模型,并对采用不同控制模型的通风效果进行MATLAB仿真模拟分析,根据通风效果确定出隧道施工通风系统的最优控制模型。
1 案例隧道施工通风情况
1.1 基本参数
本文以某隧道施工通风系统为例,根据TB 10304—2020《铁路隧道施工安全技术规程》和JTG/T 3660—2020《公路隧道施工技术规范》等规范,结合隧道施工环境特征,确定隧道施工环境要素控制指标,见表1。以需风量作为控制对象,其通风计算基础参数见表2。
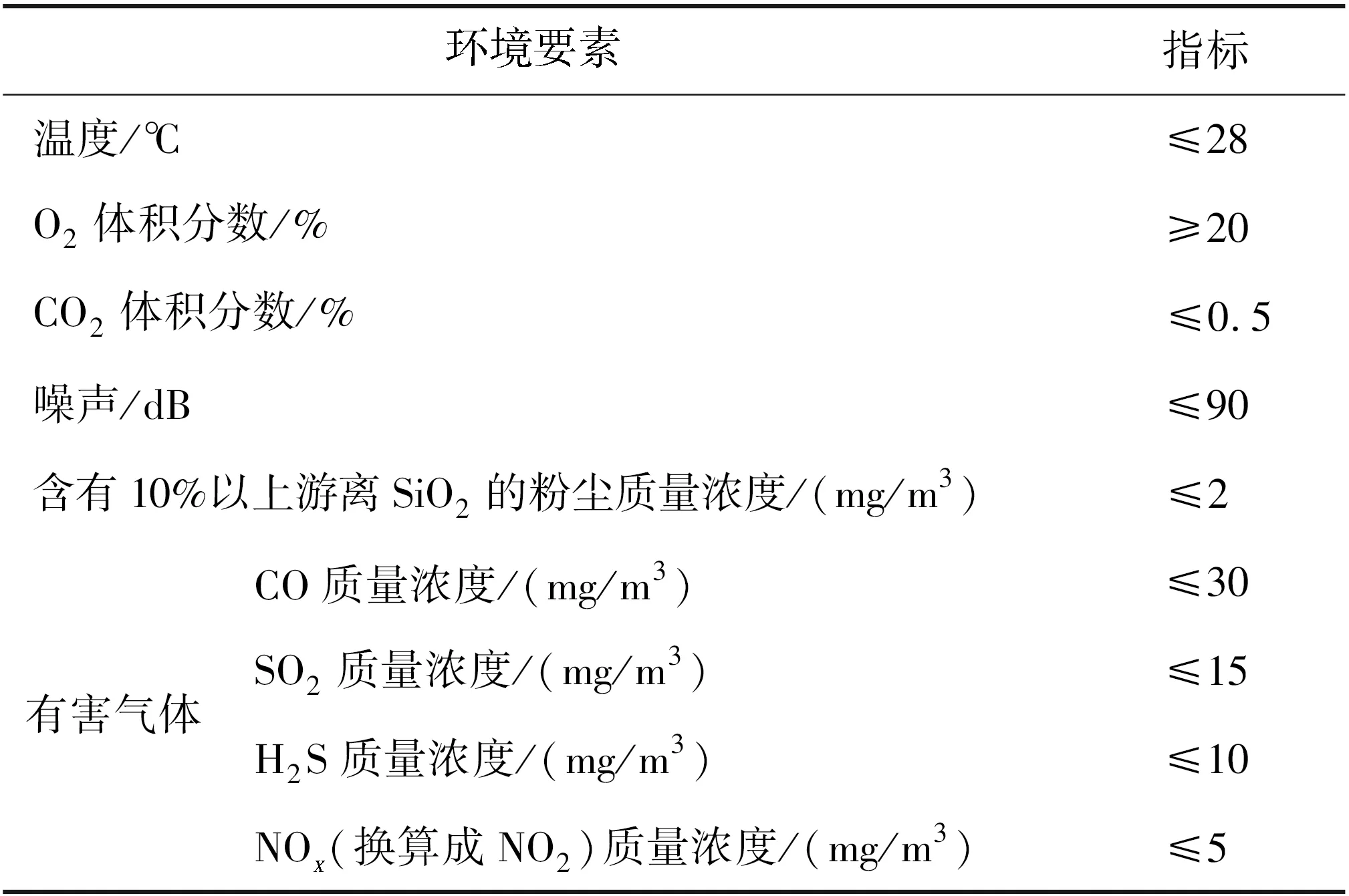
表1 隧道施工环境要素控制指标Table 1 Control indices of tunnel construction environment elements
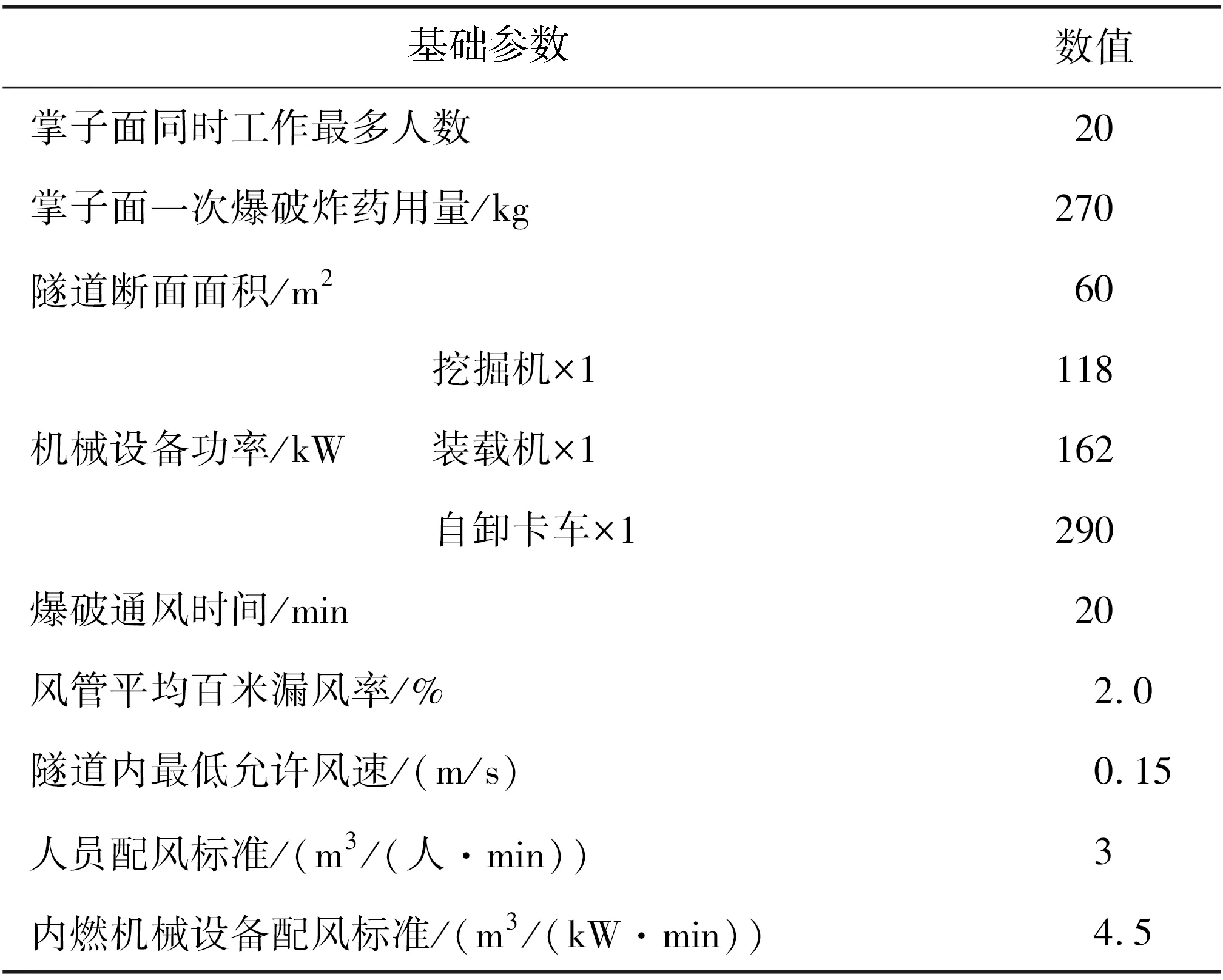
表2 通风计算基础参数表Table 2 Basic parameters for ventilation calculation
1.2 风机选配
1.2.1 隧道需风量计算
1)施工人员需风量
Q人=q人·n。
(1)
式中:q人为人员配风标准,m3/(人·min);n为人数。
2)通风长度
(2)
式中G为爆破炸药用量,kg。
3)爆破排烟需风量
(3)
式中:t为通风时间,s;A为掌子面开挖面积,m2;b为炸药产生的CO,一般取40 L/kg;Pq为通风区段内通风管始末端风量之比,为了简化计算取1;Ca为要求达到的CO体积分数,接触时间小于30 min可取0.008%,长时间接触取0.002 4%。
4)内燃机作业需风量
QM=k1·k2·H·q。
(4)
式中:k1为内燃机功率使用有效系数,取0.6;k2为内燃机功率工作系数,取0.8;H为内燃机总功率,kW;q为内燃机单位功率供风量,m3/(kW·min)。
5)洞内最低风速需风量
QW=60·Amax·v。
(5)
式中:Amax为隧道最大开挖面积,m2;v为洞内允许最小风速,取0.15 m/s。
6)隧道需风量计算结果见表3。

表3 隧道各部分需风量Table 3 Air demand of each part of tunnel m3/min
以上计算结果最大值作为掌子面的理论需风量Q需,即1 231 m3/min。
1.2.2 风机选配
风机所需风量
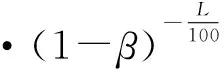
(6)
式中:β为风管百米漏风率,取2%;L为最大通风长度,m。
风管风阻
(7)
式中:λ为摩阻系数;ρ为空气密度,kg/m3;d为过风断面当量直径,m。
风机所需风量及风管风阻计算结果见表4,风机选配见表5。
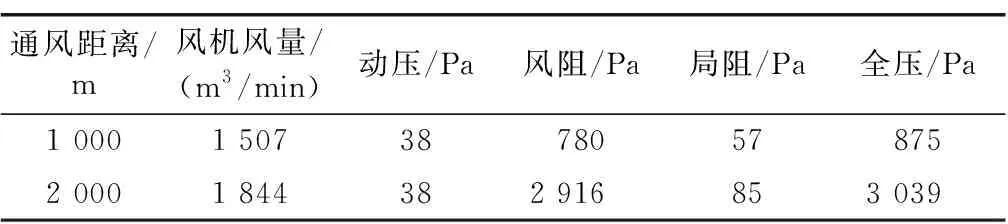
表4 风机风量及风管风阻计算表Table 4 Calculation parameters of fan air volume and air drag in pipe

表5 风机选配参数表Table 5 Fan parameters
2 隧道施工CO-需风量理论模型
隧道施工环境中的有害气体主要来自于爆破工况下的炮烟和出渣工况下的机械尾气,其主要成分有CO、CO2、NOx、SO2等。本文以CO为研究对象,建立不同工况下隧道内各断面CO体积分数随时间变化的关系模型。
2.1 爆破工况下CO-需风量理论模型
针对压入式通风系统爆破工况下CO体积分数变化规律,大多数学者有以下几个观点[9-12]:
1)隧道掌子面爆破后,在通风排烟过程中,CO在隧道内以气团的形式存在,气团中心CO体积分数高,气团两边CO体积分数低。
2)风管口至掌子面之间分为射流区、回流区和涡流区,涡流区对CO气团具有一定的滞留作用。
3)同一断面的CO体积分数在达到峰值后与通风时间呈负指数关系。
4)在远离掌子面的流场稳定区,CO气体运移距离与通风时间呈线性关系,断面CO峰值移动速度接近隧道内平均风速。
5)CO气体向外排出的整个过程可以分为分子扩散、随流扩散和紊动扩散。
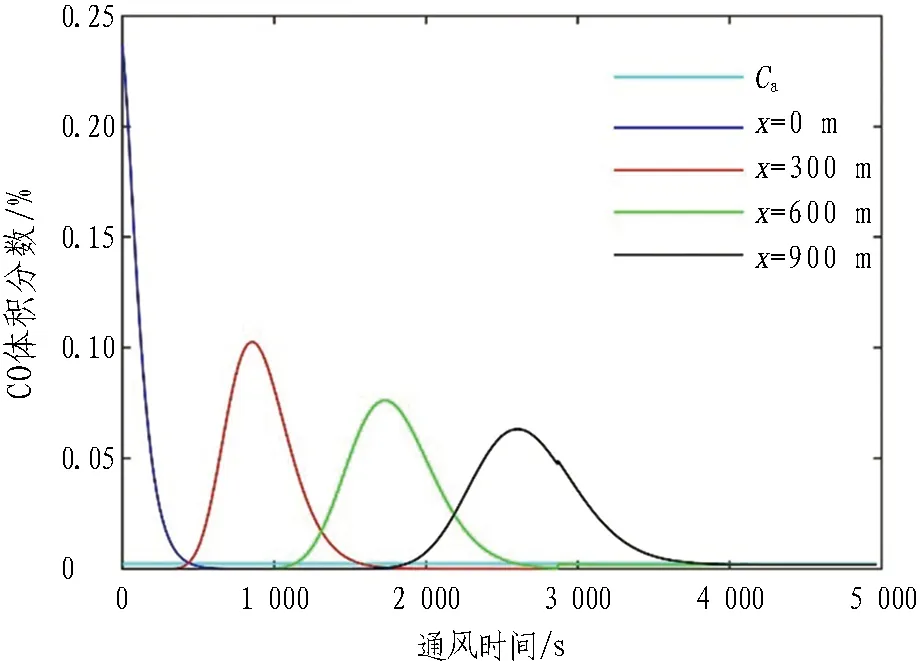
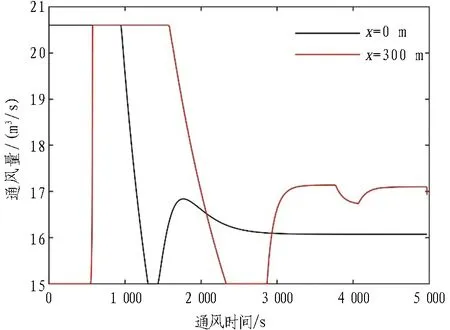
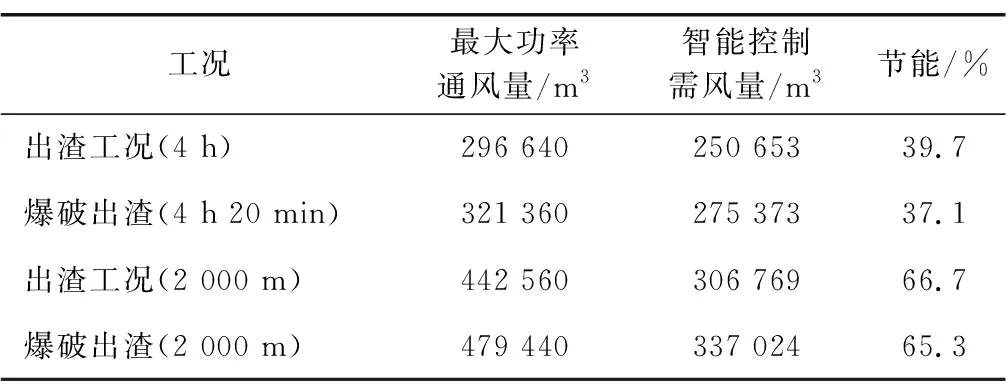
2.1.1 0 爆破产生巨大冲击可以使炮烟短时间内迅速充满靠近掌子面附近的空间,并和附近的空气进行充分混合。假设此时CO均匀分布在此爆破炮烟抛掷区域,基于稀释理论,CO体积分数[13] (8) 式中:x为与掌子面距离,m;Lt为炮烟抛掷长度,取15+G/5,m;C0为爆破后炮烟抛掷区内CO平均体积分数,%;Q为实际供风量,m3/s; Δt为单位时间,s。 2.1.2Lt 爆破产生的CO气团在最初始时随着爆破冲击快速远离掌子面并与空气充分融合,初始动能快速消耗,之后CO气团在受到流场作用远离涡流区,并且其中心运移速度约为风速时,CO气团与气流相对静止,直至掌子面对CO气团影响约束极弱,此时可以看作CO瞬时点源一维随流扩散。 瞬时点源一维随流扩散方程为 (9) 解为 (10) 式(9)—(10)中:D为CO-空气扩散系数,m2/s;u为隧道流场稳定区平均风速,m/s;ts为受爆破影响的修正系数,s。 由式(10)可知,CO-空气扩散系数对CO运移扩散浓度场分布形状和CO气团中心体积分数峰值有影响。CO-空气扩散系数通常由试验测得,在公路隧道运营通风环境下,其值近似取2.3 m2/s[14],而隧道施工通风环境流场没有大量车流,扰动更稳定,其值虽略小于2.3 m2/s,但可满足模型测试调节需求。 出渣工况下,CO的排放主体主要是挖掘机、装载机和自卸卡车等施工机械,作为污染连续点源,CO体积分数变化特点如下[15-16]: 1)不同车速行驶过程中,CO体积分数超过规范的区域极小,出渣工况下CO体积分数超限主要是施工机械CO排放累积而导致的。 2)机械行进过程中,其排放的CO体积分数在沿排气管轴线30 m内呈指数型减小,之后趋于稳定。 2.2.1 掌子面附近 在整个出渣工况,掌子面一直有挖掘机、装载机和自卸卡车工作,若总CO排放量、进风量不变,CO与附近的空气时刻充分融合,则有 (11) 式中qA为掌子面机械CO排放量,m3/s。 相较于爆破工况下掌子面CO体积分数变化,此时仅增加了qA的CO污染量,若式(8)中C0与式(11)相等,且存在区域X同时有式(8)和式(11)前提条件的污染源,即区域X中CO的初始体积分数为C0,时刻产生qA体积的CO,进风量为Q,且与污染物实时充分融合,则此时区域X中的CO体积分数时刻保持不变,连续点源对X区域内的影响为 (12) 2.2.2 机械进出隧道 若不考虑机械形体对隧道流场的局部影响,忽略尾气刚排出时的初速度,以自卸卡车为参考系,则流场等效速度 ut=u+um。 (13) 式中:u为隧道内风速,m/s;um为机械移速,m/s。 连续点源一维随流扩散方程可以看作对瞬时点源一维随流扩散方程从0到t的积分。 当t→∞时,式(8)从0到t积分的解为 (14) 式中qt为移动机械CO排放量,m3/s。 综上,本文建立了爆破工况和出渣工况下隧道区间CO一维扩散模型。相比理论分析和数值模拟,隧道现场情况复杂多变,整个隧道内流场还会受到人员、机械等因素影响,紊流不仅发生在掌子面附近,还发生在整个隧道流场,这将导致CO受到的扩散作用更强。具体表现为: 在爆破后,通风时间越长,隧道现场测量值与数值模拟所得到的整个隧道的CO峰值相比越小,整个CO体积分数的分布曲线更加平缓[17]。 隧道施工CO-需风量理论模型与实际情况有一定差别,但是其变化规律与实际相符,可以满足对控制系统检验和调教的需求。结合1.1节中的隧道施工通风系统,在隧道一直保持最大需风量的情况下,通过将第1节中隧道施工通风设计数据代入建立的理论模型(即式(8)和式(10)),计算得到掌子面附近和距掌子面300、600、900 m处CO体积分数随时间变化情况,如图1所示。 图1 爆破后各隧道断面CO体积分数随时间变化曲线图Fig. 1 Changing curves of CO volume fraction with time at each tunnel cross-section after blasting 由图1可知,爆破后通风30 min并不能使全尺寸隧道CO体积分数满足规范要求,与实际隧道施工进洞时间是冲突的,但施工通风系统应确保施工人员长时间施工的区域环境满足规范要求,据此对施工通风控制系统测试模型调整如下: 1)隧道污染物监测点。选择掌子面附近和距掌子面300 m处作为CO监测点,可以较全面地反映隧道施工区内的情况。 2)模拟时长及工况。隧道距掌子面300 m内,爆破通风3 000 s后机械尾气污染占据主导地位,且2 000 s内空气可完全换新。总模拟时长为4 970 s,爆破排烟20 min,机械出渣60 min,自卸卡车20 min进出1次隧道。 3)监测信号。即控制系统输入信号,其信号采样频率为1 Hz,为模拟隧道施工系统的动态性等特点,监测值为模型预测值C(x,t)与[0.5,1.5]正态分布的伪随机数的乘积。 4)输出信号。模拟输出为风管口需风量,不考虑隧道长度和风管漏风情况。 根据第2节中得到的CO-需风量理论模型可知,需风量与CO体积分数呈非线性负相关,为了提高控制效果,假定二者为反比例关系,将CO体积分数测量值与允许值的比值作为控制指标,有 (15) PID(proportional integral derivative)控制即比例积分微分控制,是根据监测值与设定值之间的误差比例Kp、积分Ki和微分Kd进行控制的闭环反馈控制系统。其离散的位置式PID控制算法为 (16) 式中:Kp为比例常数;Ki为积分常数;Kd为微分常数;e[i]为第i采样时刻,给定值r(t)与测量值之差;u[n]为第n采样时刻,PID控制器的输出信号。 结合式(14)有 (17) 模糊算法(fuzzy algorithm)是由模糊化、模糊推理和去模糊化3个功能模块和知识库构成的一种智能推理算法。Fuzzy PID控制即模糊PID控制[18],是利用模糊算法来自整定PID中Kp、Ki和Kd系数的一种控制方法。控制模型设计流程如下: 1)选择CO监测值的偏差e及偏差的变化ec为输入,Kp、Ki和Kd系数作为输出。 2)将输入和输出分别进行论域变换。 3)定义模糊集合并确定相应的隶属度函数。 4)建立Kp、Ki和Kd各自与e和ec的模糊规则。 5)采用重心法(普通加权平均法)去模糊化确定Kp、Ki和Kd的值。 结合隧道施工通风系统的特点将偏差e进行非线性论域变换为 (18) 取偏差e的论域中[-3,3]作为控制子集,论域中元素小于-3取-3,则此时CO体积分数小于1/4允许体积分数Ca;大于3则取3,此时CO体积分数大于4倍允许体积分数Ca。e、ec、Kp、Ki和Kd的论域均划分为{-3,-2,-1,0,1,2,3}7个等级,对应的模糊子集为{NB, NM, NS, ZO, PS, PM, PB}。 基于径向基函数的神经网络即RBF神经网络(radial basis function neural network)自整定PID控制[19]是指,在系统运行过程中利用RBF神经网络根据PID 3项输入值,确定Kp、Ki和Kd系数最优值,神经网络整定指标 (19) 采用梯度下降法确定PID中Kp、Ki和Kd系数,其调整量为 (20) 爆破通风1 200 s后开始出渣,分别以掌子面附近监测点和距掌子面300 m处监测点为控制点,采用PID控制模型进行仿真模拟,不同控制点隧道施工需风量变化曲线见图2。 图2 PID控制模型下不同控制点隧道施工需风量变化曲线Fig. 2 Changing curves of air demand for tunnel construction at different control points under PID control model 由图2可知,爆破、出渣工况下通风时间和需风量与监测点即控制点密切相关。爆破工况下,控制点距离掌子面越远,通风时间越长; 出渣工况下,控制点距离掌子面越远,需风量越大。所以根据施工区域合理选取监测点对于实现低碳目标具有重要意义。本文采用掌子面附近监测点和距掌子面300 m处监测点的CO体积分数最大值作为控制点。 在不考虑监测数据波动(见2.3节3))的前提下,不同控制模型隧道CO体积分数仿真结果见图3,隧道通风量仿真结果见图4。输入信号条件为2.3节2),不同控制模型监测波动情况下隧道通风量仿真结果见图5。3种控制模型响应时间、振荡时间及标准差见表6。 图3 不同控制模型隧道CO体积分数仿真结果图Fig. 3 Simulation results of CO volume fraction in tunnels in different control models 图4 不同控制模型隧道通风量仿真结果图Fig. 4 Simulation results of tunnel ventilation volume in different control models (a) Fuzzy PID和PID控制对比图 (b) RBF-PID和PID控制对比图图5 不同控制模型监测波动情况下隧道通风量仿真结果Fig. 5 Simulation results of tunnel ventilation volume under monitoring fluctuation in different control models 表6 不同控制模型仿真数据表Table 6 Simulation data of different control models Kp、Ki和Kd参数初始值调节过程中,在图3横坐标1 000 s处左右输出值不产生振荡的前提下,Kp选取最大值,这时PID控制模型虽然响应较快、性能较好,但在实际工程中参数难以校准且抗干扰能力差。 RBF-PID控制模型相较于Fuzzy PID控制模型响应更快,这是因为RBF神经网络能实时根据CO体积分数及其变化预测下一时刻的需风量,而Fuzzy PID控制模型则主要是根据经验设置的模糊规则调节需风量,同时这也导致了Fuzzy PID控制模型抗干扰能力更强,RBF-PID控制模型抗干扰能力较弱,振荡时间长。 上述3种控制模式下总需风量分别为90 331、90 325、90 328 m3,风量和能耗成3次方的关系,节能效果相近,现选取Fuzzy PID控制模型的仿真数据进行节能效果分析。实际施工过程中,风机虽然有少量档位可以调节,但是随着工况的变化、掘进过程中通风长度的增加以及通风环境中的动态变化,传统手动调节风机需要施工人员判断施工环境,很难满足实际需求。出渣工况作为隧道通风量设计最危险工况,而通风设计计算原理是将新鲜风把刚生成的污染物稀释到规范限值以下,与实际情况不符,没有考虑到施工机械工作的动态性以及污染物在隧道内的运移扩散规律,相对于调节至最大风量,采用隧道施工通风智能控制系统节能效果显著,1 000 m长隧道可节能37.1%以上,2 000 m长隧道可节能65.3%以上。智能控制节能效果对比见表7。 表7 智能控制节能效果对比表Table 7 Comparison of energy-saving effects of intelligent control 本文建立了隧道施工爆破和机械出渣下CO-需风量理论模型,据此确定了隧道施工通风控制系统数字仿真模型,并对PID控制、Fuzzy PID以及RBF-PID3种控制模型进行MATLAB仿真分析,得到结论如下: 1)本文所建立的CO-需风量理论模型可反映实际隧道施工过程中CO体积分数数值变化情况以及其变化规律。 2)由于隧道施工爆破通风主要以CO气团运移为主,因此根据施工区域确定环境控制区,即有害气体监测区是施工通风智能控制的重要前提条件。 3)结合隧道施工通风系统特点,将CO体积分数实测值与允许值之比作为控制系统的控制指标,将控制关系近似线性化,可以极大地增强控制模型性能。 4)控制模型性能和抗干扰性有一定的负相关性,本文中PID控制模型由于参数调节的便捷性使其在理论响应性能上较为优异,但Fuzzy PID控制模型或RBF-PID控制模型可更好地响应实际工程对于抗干扰和性能的需求。 5)采用智能控制的隧道施工通风系统节能效果显著,且随着隧道长度的增加,其经济性愈发明显。 隧道施工通风环境智能控制不能仅停留在单一隧道、单一工程,接下来应该深入研究隧道施工通风规律,提出一套系统的、适应性强的隧道施工通风智能控制系统。2.2 出渣工况下CO-需风量理论模型
2.3 施工通风控制系统测试模型
3 控制模型优化研究
3.1 PID控制模型
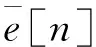
3.2 模糊自整定PID控制模型优化
3.3 RBF神经网络自整定PID控制模型优化
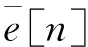
4 控制模型仿真分析
4.1 施工通风系统监测点分析
4.2 控制模型响应分析
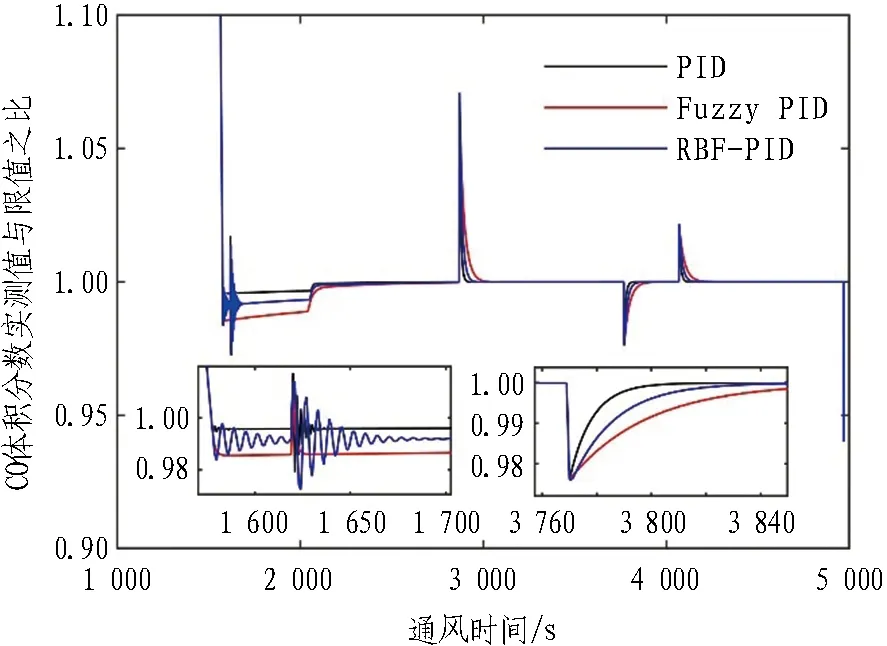
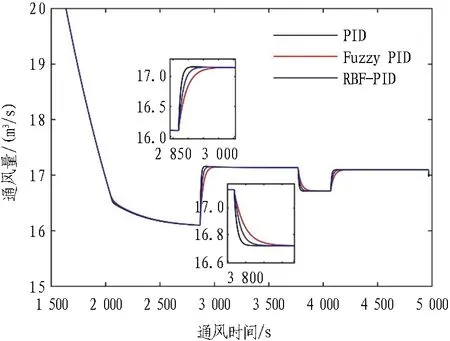
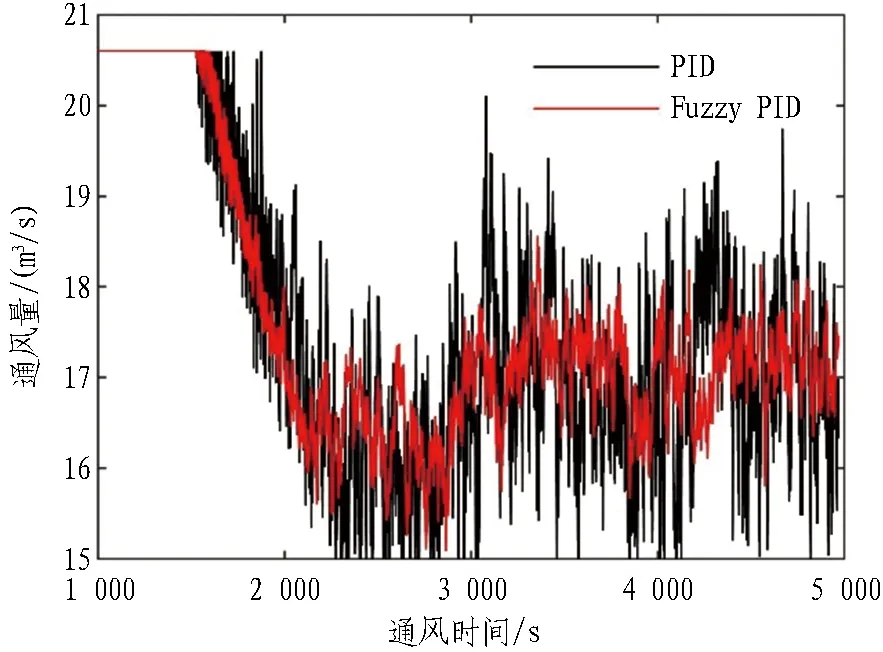
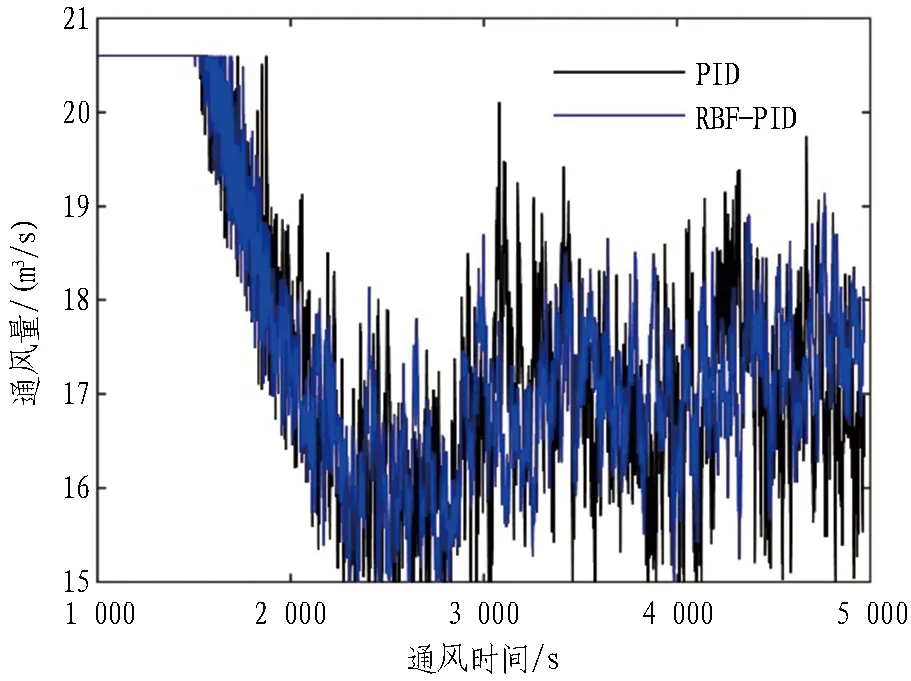

4.3 控制模型能耗分析
5 结论与建议

