隧道磁共振旋转探测二维成像方法

刁 庶, 梁文婧, 徐奡澍

(1. 无锡职业技术学院控制技术学院, 江苏 无锡 214121; 2. 吉林大学仪器科学与电气工程学院, 吉林 长春 130061; 3. 重庆电子工程职业学院, 重庆 401331)

0 引言

磁共振探测技术是一种能够直接定量探测地下水的地球物理方法[1]。与其他隧道超前探测技术相比,其具有直接、分辨率高等特点[2-5]。由于该方法能够快速准确地定位水源位置和评估水量大小,近年来被广泛应用于水资源勘探、水文环境监测以及地下工程水害预警等领域。

随着磁共振探测技术在一维空间数据解释研究方面的日趋稳定,2005年,Braun等[6]第1次引入了二维核函数的概念,得到了二维磁共振探测结果,分辨率良好,为后续二维反演方案的拟定提供了理论基础。随后,Hertrich等[7]研究了一种快速二维磁共振成像反演方法,并通过试验数据验证了该方法的有效性,仿真结果表明该方法能够准确还原原始模型的重要特征。林君等[8]提出了基于优化Block反演的地面磁共振成像方法,反演结果满足精度和稳定性要求。林婷婷等[9]引入横向约束反演思想,提高了磁共振解释结果的准确性,加强了剖面地质结构和含水模型探测的连续性。Jiang等[10]研究了一种基于QT反演方法的磁共振层析数据二维成像技术,通过分辨率分析可知,使用复杂层析数据不仅可以提高分辨率,还可以增加穿透深度,且得出了该方法对不断增加的噪声条件不太敏感的结论。进一步,蒋川东[11]采用初始振幅反演方法对德国Einersberge湖进行了三维地下水成像和含水量估计,完成了三维高精度成像。Legchenko等[12]、Vincent等[13]对法国阿尔卑斯山脉鲁塞冰川的溶洞进行了三维磁共振成像,并通过20个钻孔数据对探测结果进行了验证。Costabel等[14]利用磁共振含水率和弛豫时间的岩性指标,识别出薄含水层、细砂土含水层和粗砂土含水层,利用磁共振技术估算的岩性信息补充了现有的钻孔数据,极大地改善了Langeoog岛的水文地质模型成像精度。由以上文献可知,地面磁共振探测数据反演方法已经可以对三维数据进行解释,并向高分辨率、高精细方向发展。

针对地下探测工程中的磁共振数据解释,顾汉明等[15]提出了通过增加隧道探测天线匝数来提高信号强度进而提高反演效果的方法;Girard等[16]研究了矿井下磁共振探测突水,并进行了正演计算,得出未获得磁共振信号难以对含水体成像的结论;林君等[17]深入研究了地下水超前探测理论、准全空间模型建立与反演方法,实现了对隧道工程和煤矿开采等地下狭窄空间极端环境的探测;Lin等[18]初步开展了地下磁共振探测准全空间的一维正反演解释;林君等[19]在地面磁共振探测理论的基础上,建立地下全空间模型,推导直立线圈的磁共振响应信号表达式,可以获得一维成像结果;Diao等[20]提出了基于2 m探测线圈扇形扫描形式的磁共振旋转探测方法,能够获得二维成像结果。

上述反演解释方法已在地面工程的应用中取得了较好的效果,可以实现三维空间成像,能够观测到分辨率清晰的含水体。然而,地下工程中的磁共振信号,由于受探测空间复杂、地下水文地质环境及场效性等影响较大,其反演解释方法目前还停留在一维空间。本文利用磁共振旋转探测方法对隧道空间非层状水的二维分布情况展开研究,针对一维成像无法定位和定量评估的问题,提出基于复包络反演的旋转探测二维成像方法,建立隧道空间二维反演目标函数。通过引入吉洪诺夫正则化因子和平滑约束条件,提高反演结果的稳定性和分辨率,解决一维探测方法探测盲区的问题,在掌子面附近的左右侧壁及顶板、底板位置分别获得溶洞及含水通道的含水量与弛豫时间高精度二维成像结果。

1 隧道磁共振旋转探测系统

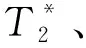
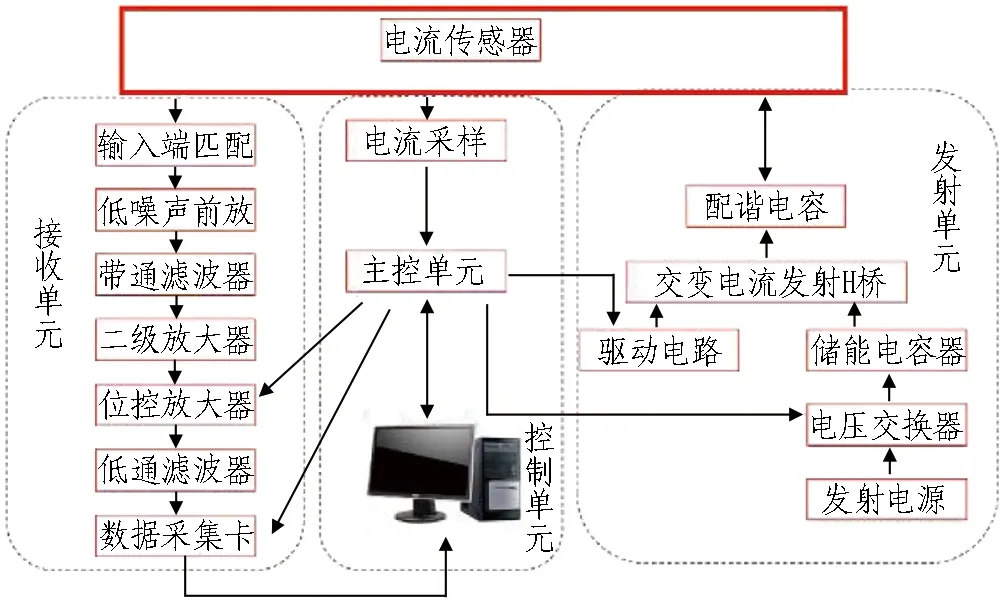
图1 隧道超前探测仪系统结构框图Fig. 1 Tunnel detection instrument system

2 隧道磁共振复包络二维反演方法

复包络反演方法是由Müller-Petke等[21]提出的,该方法使用1组脉冲矩完整的磁共振信号进行反演解释,能够得到含水量、平均弛豫时间随深度的变化情况。由于其将全部的测量包络数据一次性代入反演计算中,避免了重复计算带来的误差,从而提高了反演精度,优于目前常用的方法。

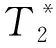
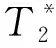
(1)

式中:q为激发脉冲矩;t为感应信号接收时间;K(q,r)为核函数;r为地下某一空间位置;w(r)为地下体积单元d3r的含水量。

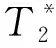
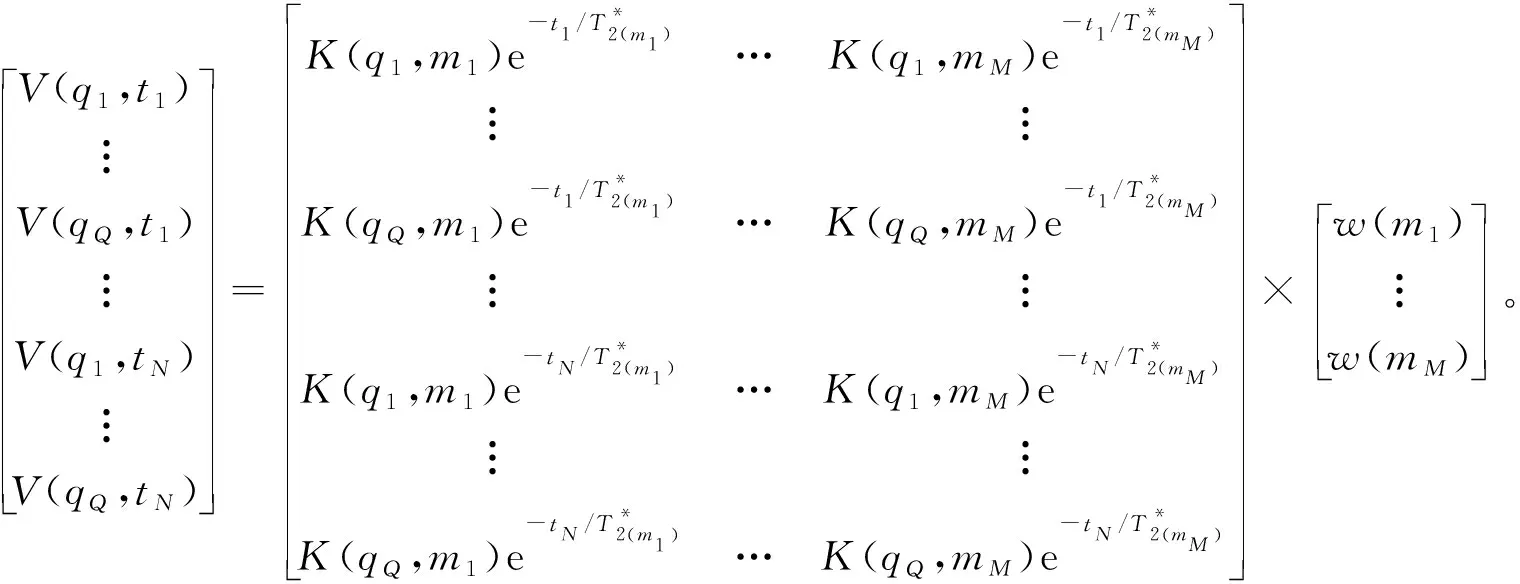
(2)

式中:Q为脉冲矩个数;N为抽道数;mi(i=1,2,3,…,M)为地下剖分单元,M为剖分单元个数。

式(2)可用于推导二维反演的雅克比转换矩阵。针对同一目标体不同脉冲矩及探测角度获取的信号同时进行复包络反演,可以提高反演二维成像结果的分辨率,提高目标体边界清晰度。旋转天线反演的目标函数为

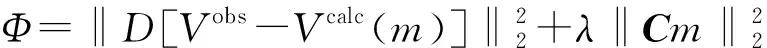
(3)

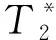
设平滑度矩阵C的单元边界是b,rb为权重因子,根据文献[25]可知其计算公式如式(4)所示。

rb=I+(rz-1)nb·ez。

(4)

式中:nb为模型平滑度矩阵C的单元边界b的法向向量;ez为z方向的单位向量;rz为含水模型权值,其值限制在[0,1];I为单位矩阵。

则具有约束条件目标函数的最优解即含水量的解,利用高斯牛顿迭代方程求解正则化标准方程,可以得到

(JTDTDJ+λCTC)Δwk=JTDTD(V-K·wk)-λCTCwk。

(5)

式中:J为雅克比矩阵;C=[1,-1];k为当前的迭代次数;wk为当前迭代次数下的含水量值; Δwk为第k次迭代时含水量的增加值;V为接收天线中弛豫信号的感应电动势V(q,t)的矩阵形式;K为核函数的矩阵形式。

3 模型仿真与反演结果

3.1 模型建立与仿真

建立的探测模型如图2所示。在右侧壁上,距离中心位置5 m处有一含水通道模型,尺寸为4 m×4 m,含水量为50%(如图2(a)所示),弛豫时间为0.5 s(如图2(c)所示);左侧壁无含水构造;在顶板上方和底板下方,距离中心位置5 m处分别存在椭圆形溶洞,溶洞内的含水量为50%(如图2(b)所示),弛豫时间为0.5 s(如图2(d)所示),外部为无水区。设定仿真数据的噪声水平为100 nV,脉冲矩为0.04～4 As。

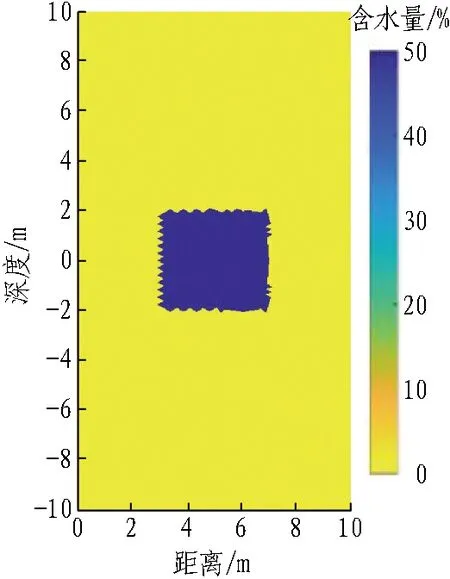
(a) 右侧壁含水通道含水量模型

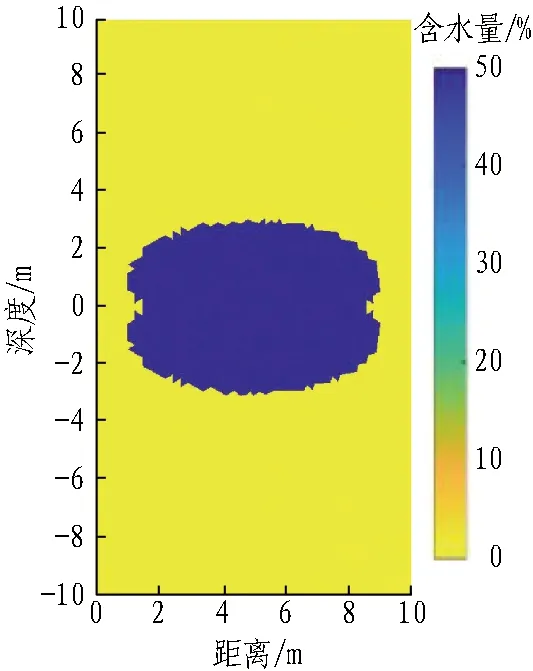
(b) 顶板、底板溶洞含水量模型

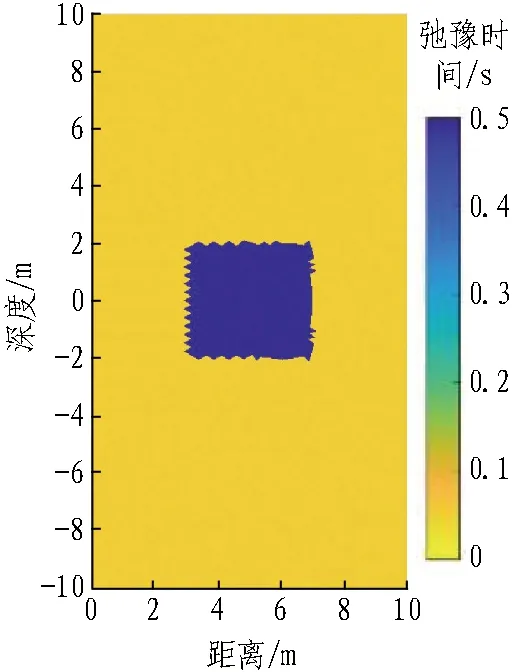
(c) 右侧壁含水通道弛豫时间模型

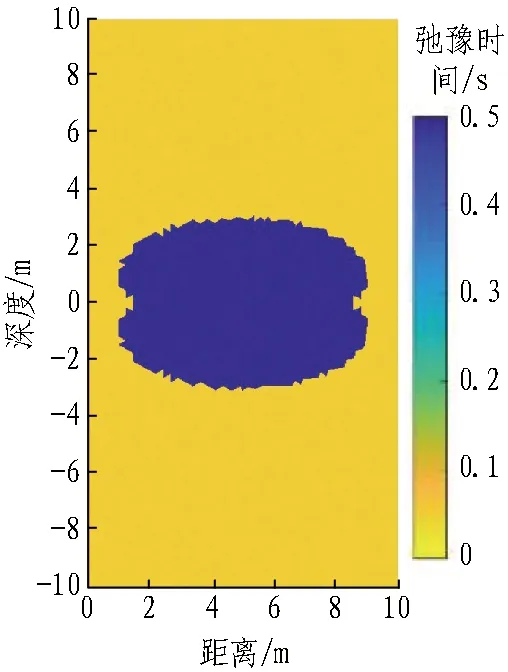
(d) 顶板、底板溶洞弛豫时间模型图2 隧道全空间旋转探测水害隐患含水量及弛豫时间正演模型Fig. 2 Forward modeling of water content and relaxation time for tunnel full-space rotation detection of water hazards

旋转探测隧道全空间示意如图3所示。首先,使探测线圈平面平行于掌子面,对掌子面前方含水体进行仿真(如图3(a)所示),旋转天线以水平方向x轴为旋转轴,绕z方向每隔22.5°逆时针旋转1次,共旋转8次,旋转180°,即可完成对掌子面前方含水体的探测。然后,将旋转天线水平移动至左侧壁,对左侧壁含水体进行仿真(如图3(b)所示),探测天线以水平方向y轴为旋转轴,绕z方向每隔22.5°逆时针旋转1次,共旋转8次,即可完成对左侧壁含水体的探测;同理,移动天线至右侧壁,即可完成对右侧壁含水体的探测。最后,将探测天线平行于地面,探测天线以水平方向z轴为旋转轴,绕y方向每隔22.5°逆时针旋转1次,共旋转8次,即可完成对隧道顶板含水体的探测;同理,反方向即可完成对底板含水体的探测。

(a) 掌子面(b) 侧壁(c) 顶板及底板图3 旋转探测隧道全空间示意图Fig. 3 Tunnel full-space schematic of rotation detection

3.2 反演结果与分析

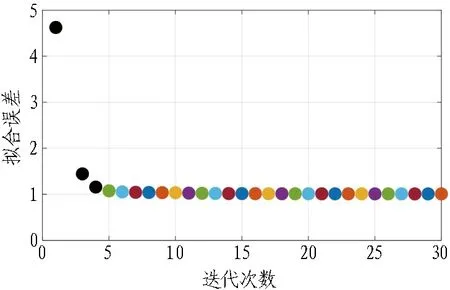
(a) 观测数据集合

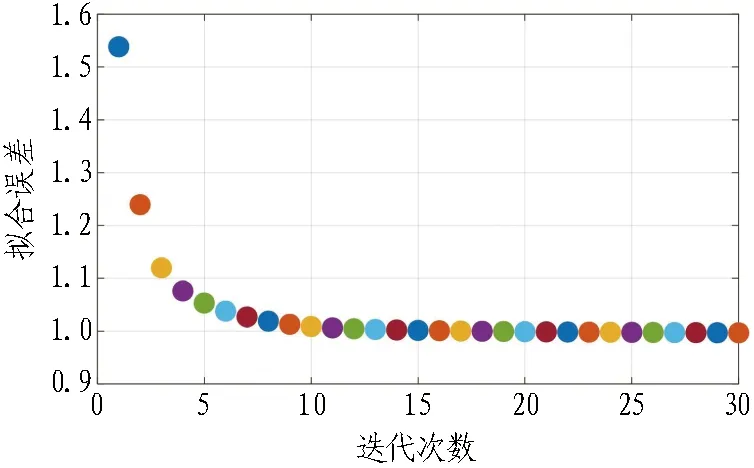
(b) 噪声水平加权的观测数据与计算数据不吻合度图4 观测数据结果Fig. 4 Analysis of observational data results

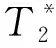
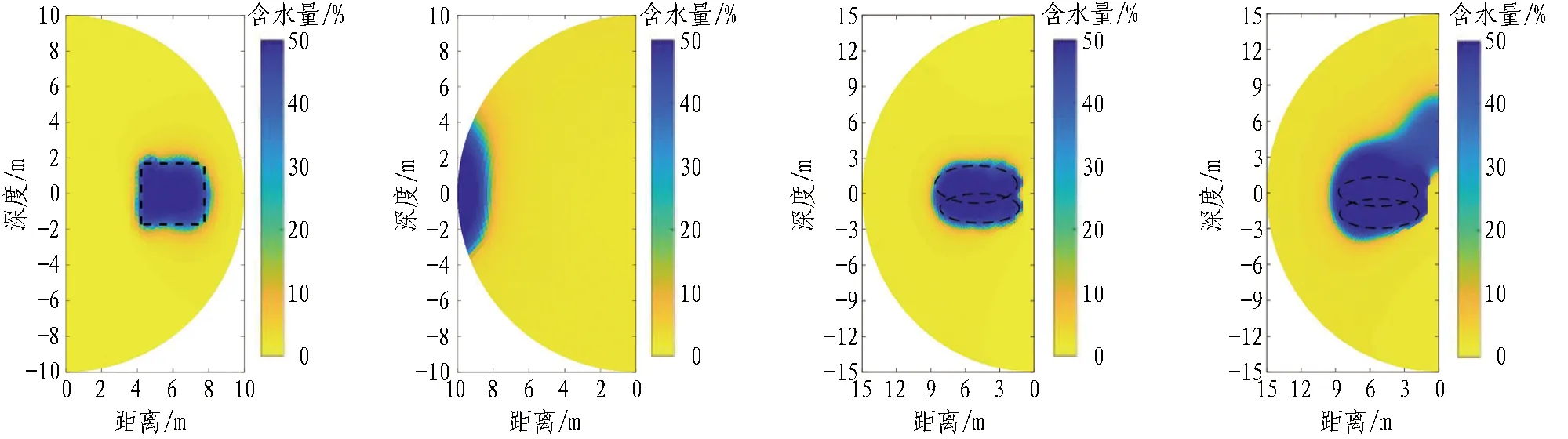
(a) 右侧壁含水通道含水量模型(b) 左侧壁含水量模型(c) 顶板溶洞含水量模型(d) 底板溶洞含水量模型

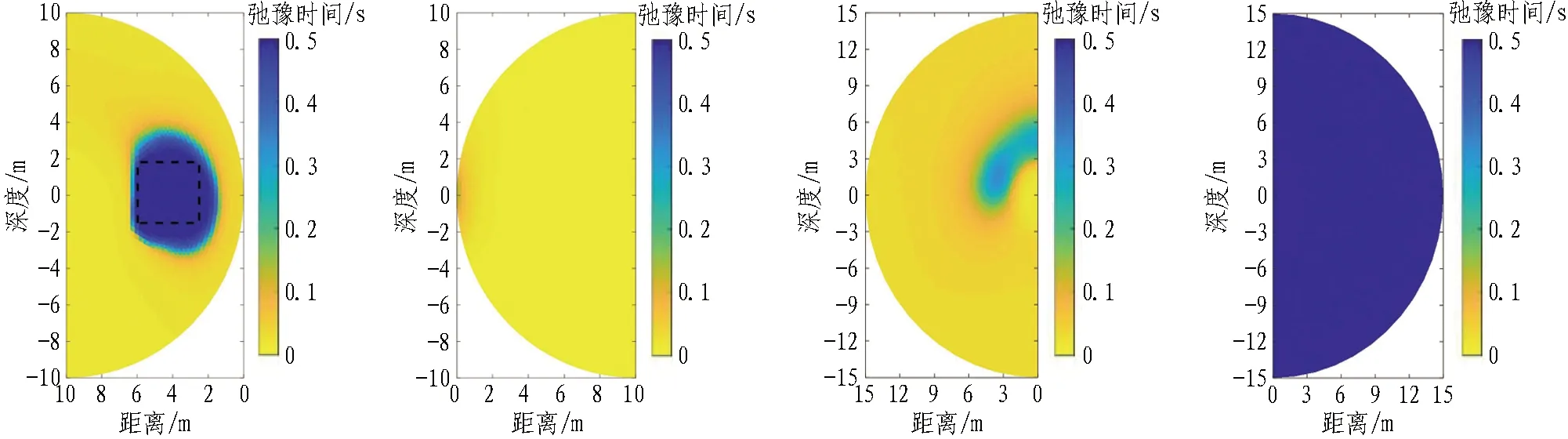
(e) 右侧壁含水通道弛豫时间模型(f) 左侧壁弛豫时间(g) 顶板溶洞弛豫时间模型(h) 底板溶洞弛豫时间模型图5 隧道全空间旋转探测水害隐患含水量及弛豫时间分布情况Fig. 5 Distribution of water content and relaxation time for tunnel full-space rotation detection of water hazard hazards

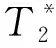
4 结论与建议

本文采用磁共振旋转探测方法对隧道水害隐患进行准确定位及二维高精度成像,并建立了隧道空间二维反演目标函数,最后对隧道3种水害隐患模型进行了验证,得到的主要结论如下:

1)针对一维成像难以定位和定量评估的问题,提出基于复包络反演的旋转探测二维成像方法,通过引入吉洪诺夫正则化因子和平滑约束条件,提高了反演结果的稳定性和分辨率。

2)针对隧道空间狭小无法移动探测线圈的问题,设计了旋转探测系统,通过分析采集数据中的地下磁共振信号,定量估计目标水体的位置、含水量大小、弛豫时间、含水体所赋存的结构等水文地质信息。

3)采用磁共振旋转探测技术在隧道超前探测中进行了模拟试验,利用复包络反演方法实现了隧道水害隐患的二维高精度成像,分别得到了右侧壁上距离中心位置5 m处、顶板上方距离中心位置5 m处和底板下方距离中心位置5 m处存在含水结构的结果,实现了溶洞、含水通道的水害隐患高精度二维含水体重构。

下一步,建议通过改进隧道磁共振二维正演计算方法,提高反演计算效率,实现隧道水害隐患现场的快速成像。