富水砂性地层中地墙渗漏诱发地层塌陷灾害的细观机制探讨

晁 慧, 谭 勇, 刘天任

(同济大学地下建筑与工程系, 上海 200092)

0 引言

伴随着我国城市化进程的不断推进,城市人口众多、绿地面积不足、交通拥堵等问题亟待解决,开发地下空间作为解决“大城市病”的关键举措,在近年来得到迅速发展[1-2]。由于基坑工程是地下空间开发的前提条件[3],其安全施作受到人们的广泛关注[4-5]。其中,由地下连续墙(文中简称地墙)渗漏引发的基坑工程事故占比较大[5-8],需谨慎对待,尤其是在富水砂性地层中,因其地下水位高、坑内外水头差大、土体黏聚力低、渗透性强、自稳性差,土颗粒极易在动水力作用下发生流失,造成基坑失稳、邻近建筑物不均匀沉降等灾害。

针对基坑工程中的地墙渗漏事故,许多学者从案例分析、数值模拟等方面进行了深入研究。在案例分析方面,樊冬冬等[6]基于渗漏段监测数据及围护结构设计,分析得出地下水由地墙钢筋加密段进入坑内,导致了基坑渗漏事故的发生;Ni等[7]介绍了基坑挡土墙渗漏引起管涌事故及应急处理的过程,指出做好灾害防控和监测预警的重要性;Tan等[8]分析了软土地区某深基坑渗漏事故发生的原因,并对地下水渗流路径及地表沉降区域进行了研究和绘制;赵云非等[9]综合分析了城市地铁深基坑施工渗漏水高发的原因,提出了相应的预防措施。在数值模拟方面,胡琦等[10]基于有限元方法和土体试验成果,提出了考虑渗流、开挖卸荷、围护结构变形共同作用的基坑工程渗漏破坏分析方法;戴轩等[11]基于CFD-DEM方法对基坑工程漏水漏砂引发的地表变形规律、地层损失率的发展变化规律以及地层深层位移变化规律进行了总结。

上述研究涉及地墙渗漏的发生原因、事故影响、地层损失规律及防治措施等方面,为基坑地墙渗漏灾害的防治提供了必要的指导。然而,发生在富水砂性地层中的地墙渗漏,呈现出事故前监测数据无明显预兆、发展速率快、地层损失严重的特点,采用数值模拟的方法探讨灾害的发展过程,建立的三维离散元模型可以从空间角度探寻地层塌陷的细观机制,同时,经验证的数值模型可以在其基础上进行变参分析,进一步提高对灾害演化机制的理解,为实际工程提供帮助。

本文基于南通市某地铁深基坑工程地墙渗漏事故实例,采用CFD-DEM流-固耦合模拟方法,对地墙渗漏诱发的地层塌陷灾变过程进行细观分析,以期相关研究成果为精准防灾提供参考。

1 工程概况

1.1 工程简介

本文所研究的地墙渗漏事故基坑为江苏省南通市某地下轨道交通车站基坑工程。基坑主体由西端头井、标准段、东端头井组成,拟建车站为地下2层框架结构,车站净长180 m,净宽19.3 m,标准段基坑开挖深度为17 m,采用半盖挖顺作法施工。基坑工程平面图如图1所示。

1.2 工程及水文地质条件

基坑工程建设地地貌类型单一,属冲—海积新三角洲平原地貌类型。根据勘察结果并结合区域地质资料,基坑工程在勘察深度范围内分布的地层主要为第四系全新统(Q4)地层、第四系上更新统(Q3)地层,自上而下分为4个大层,6个亚层,依次为: ①杂填土层,②砂质粉土层,③-1粉砂夹砂质粉土层,③-2粉砂层,③-4粉细砂层,⑥粉砂层。各土层主要物理力学性质见表1。

表1 土层物理力学性质Table 1 Physico-mechanical parameters of soil layers

地表水系发育,地下水接受长江水位、大气降水补给,潜水主要赋存于①层、②层、③-1层、③-2层和③-4层中,对工程质量影响较大。潜水稳定水位埋深为0.4～2.3 m,根据区域水文资料,潜水位年变化幅度一般为1～2 m。地下水位较高,基坑进行土方开挖时需保证坑内水位在开挖面以下1.0 m。

1.3 渗漏事故简介

2019年3月30日,基坑标准段北侧测斜监测点CX12附近地墙发生渗漏,渗漏点在开挖面附近。渗漏区域附近围护结构剖面图如图2所示,采用厚度为800 mm的地墙,总深度约40 m,其中下部7.5 m范围内为素混凝土墙;共设置4道支撑,其中第1道为截面尺寸0.8 m×1 m的混凝土支撑,第2～4道为钢支撑(φ609)。渗漏发生时,基坑开挖至深度11 m附近,且渗漏点同样位于开挖面附近,此时第3道钢支撑未架设。

图2 渗漏区域附近围护结构及地质剖面图(单位: m)Fig. 2 Cross-section and soil profile near leakage zone (unit: m)

渗漏事故发生前后,地墙侧向位移随时间变化规律如图3所示,最大地墙侧向位移出现深度由12.5 m发展到16.0 m。地墙渗漏附近的地表沉降监测点D16-2和D16-3随时间变化规律如图4所示。由图可知,自2019年3月30日发生渗漏后,地表沉降均发生了突增,其中,测点D16-2(距基坑较近)日变化量达到20 mm,测点D16-3(距基坑较远)日变化量约为4 mm,这表明地墙渗漏导致坑外地层出现了严重水土流失。地墙最大侧移与位移发展关键节点关系如图5所示,通过分析可知: 从2月20日到3月30日发生渗漏前,地墙侧向位移发展平缓,主要由基坑开挖引起;3月30日渗漏事故发生,地墙侧向位移发展迅速;渗漏发展至4月3日,于开挖面附近发现面渗,施工方开始采取架设临时支撑、墙后注浆堵漏等方式控制地墙侧向位移发展,此时地墙侧向位移相比3月30日已发生较大幅度增长;截至4月10日,地墙侧移停止迅速增长,渗漏基本得到控制。由以上分析可知,在富水砂性地层中,基坑工程发生地墙渗漏将会引起围护结构侧向位移迅速发展,这与软土地层中基坑地墙渗漏引发的侧向变形增长规律有显著区别[8]。

图3 地墙侧向位移时变曲线图Fig. 3 Lateral displacement of diaphragm walls

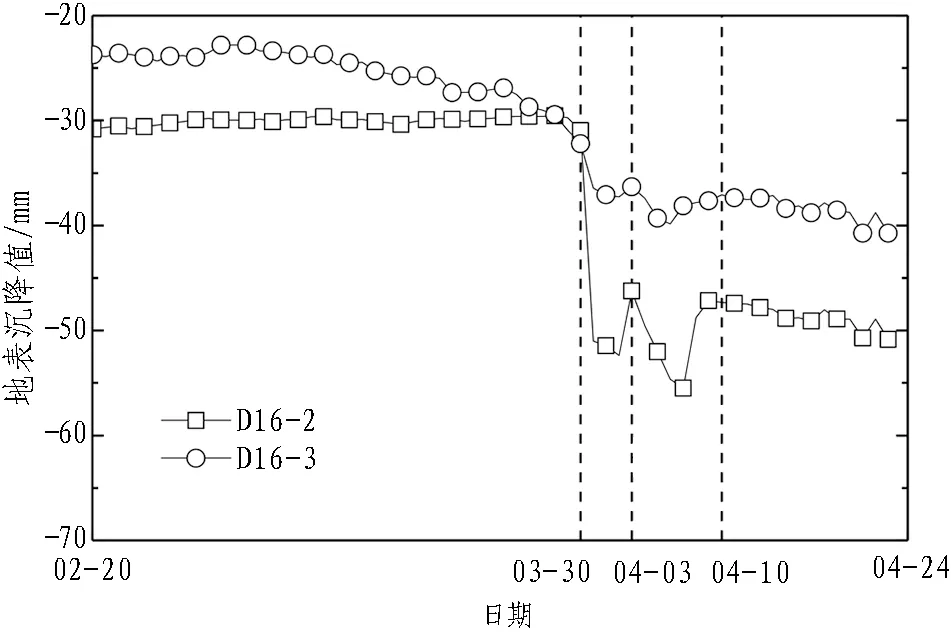
图4 2019年地表沉降监测数据Fig. 4 Monitoring data of ground settlement in 2019

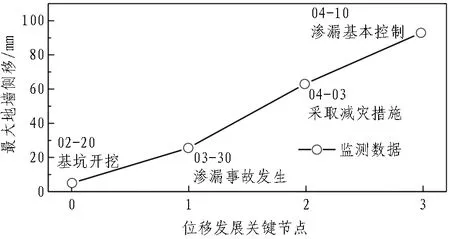
图5 2019年地墙最大侧移与位移发展关键节点关系图Fig. 5 Variation of maximum lateral wall deflections with critical working conditions in 2019

2 数值模型

2.1 CFD-DEM流-固耦合模拟方法

富水砂性地层中地墙渗漏诱发的灾害,涉及地下水和砂土的耦合作用问题。砂土作为非黏性土,其物理力学性质离散程度较高,且在地层受到扰动时呈现出非连续变形特征,适宜采用离散元方法进行模拟分析。综合考虑计算精度与计算效率,CFD-DEM方法可以较为有效地模拟大规模的宏观流-固耦合问题,戴轩等[11]、李晓蛟等[12]、刘天任等[13]已运用该方法进行了相关的模拟和研究,并结合模型试验、理论分析进行了验证。关于CFD-DEM流-固耦合方法的基本理论详见文献[12]。

2.2 模型建立

基于CFD-DEM方法建立流-固耦合模型,对本文所述渗漏事故进行模拟分析。根据渗漏事故情况,分别在PFC软件中建立基坑颗粒模型、在Fluent软件中建立流场模型并计算,得到流场结点、单元、流速、密度、黏性等数据文件,将数据文件导入PFC-CFD模块中,计算流体作用力,并施加于颗粒质心位置,从而实现流固耦合模拟。

2.2.1 DEM部分模型建立

综合考虑计算效率和准确度,选取1个标准段宽度(10 m)内的地墙和土体进行分析;由于围护结构在平面内对称,可取结构的1/2进一步简化建模; Hsieh等[14]指出由基坑开挖引起的地表沉降主要影响范围为2倍开挖深度,考虑到富水砂性地层中地墙渗漏对周边环境的影响程度较大,建模时令模型边界与地墙中心距离为3倍开挖深度。综上所述,颗粒模型长度为41 m(X方向),宽度为10 m(Y方向),高度为50 m(Z方向),模型整体几何参数汇总如图6(a)所示,图6(b)为渗漏处建模细节情况。

(a) 模型几何参数 (b) 渗漏处建模细节图6 DEM模型示意图(单位: m)Fig. 6 Schematic of DEM model (unit: m)

DEM方法通过假设微小颗粒间的接触模型,来模拟宏观响应,将从土体、支撑、地墙3部分介绍建模细节。

1)土体部分。在离散元模拟中,不同细观参数的球形颗粒相互接触形成新的接触模型时,由于参数之间继承规则以及接触生成的随机性,会导致细观与宏观参数对应关系建立非常困难。这就使得按不同土体分层建立的模型,在发生层间混合时,容易出现模拟失真的情况。在满足探讨渗漏细观机制的目标前提下,本模型将场地土层简化为均质土体,其中土体力学性质按照地层厚度进行加权平均,以体现出富水砂性地层条件的总体特征,计算得到土体平均力学参数为γ=18.8 kN/m3,c=6.4 kPa,φ=33.8°,e=0.8。采用线性模型建立颗粒间接触,通过三维三轴压缩试验数值模拟对颗粒的细观参数进行标定。当采用表2中的接触模型参数时,土体的内摩擦角为34°,相较于加权平均后的土层,误差为0.5%。颗粒粒径方面,综合考虑软件计算效率、计算精度和耦合尺寸要求,设置上部20 m深范围内的颗粒半径为0.15 m,下部30 m深范围内的颗粒半径为0.3 m。

表2 土体颗粒接触模型(线性模型)参数Table 2 Properties of contact model of soil particles (linear model)

2)支撑部分。使用1组沿直线排列的球形颗粒来模拟支撑,考虑到支撑的受力特点,主要模拟其在轴向的受力情况。由于线性接触模型只能模拟受压,在模拟过程中,当模拟支撑的颗粒之间产生相互远离的位移时,线性接触模型下,该组球形颗粒会从中断开,因此,使用线性平行黏结接触模型来对支撑的轴向受力进行模拟,并对颗粒的位移加以限制,使其只能发生轴向变形。颗粒的细观参数可类比串联弹簧计算得出,详见表3。

表3 支撑和地墙接触模型(线性平行黏结模型)参数Table 3 Properties of contact model of support and diaphragm wall (linear parallel bond model) N/m

3) 地墙部分。使用1组均匀分布在平面区域的球形颗粒来对其进行数值模拟,考虑到地墙的受力特点,主要模拟其在弯曲变形方面的受力情况,选用线性平行黏结接触模型。标定过程如图7所示,通过模拟等效悬臂梁受集中力作用情况下的挠度,并将其与解析值对比,依照上述方式进行细观参数标定。

图7 地墙标定原理示意图Fig. 7 Schematic of diaphragm wall calibration

已有研究表明[15],粒度比是影响管涌的重要因素,Zuriguel[16]在研究散粒体材料在筒仓中的阻塞问题时指出,对于无黏性球形颗粒,筒仓出口直径与颗粒直径之比大于5时,阻塞现象会消失。由于计算效率的限制,在数值模拟中对土颗粒尺寸进行了放大,为保证渗蚀现象能够顺利发生,相应地,渗漏孔洞尺寸也应与土体颗粒粒径保持相当比例。在建模过程中,渗漏区域为2 m×2 m,渗漏区域土颗粒直径为0.3 m,计算二者直径比(取正方形边长为直径)为2 m/0.3 m≈6.67>5,满足要求。综上所述,所建DEM模型颗粒总数约为30万个。

2.2.2 CFD部分模型建立

为兼顾流固耦合需求,CFD流场模型尺寸在DEM颗粒模型尺寸基础上建立。为尽量减小边界效应对流场的影响,将流场模型坑外边界扩展至距离基坑50 m远处; 流场模型底部与DEM颗粒模型底部重合。基于工程所在地水文地质条件及施工信息,确定坑外流场顶面(蓝色)为地面以下2 m,即高度为48 m; 由于基坑坑内需降水至开挖面以下1 m处,因此坑内流场顶面(红色)高度为38 m。模型示意图如图8所示。

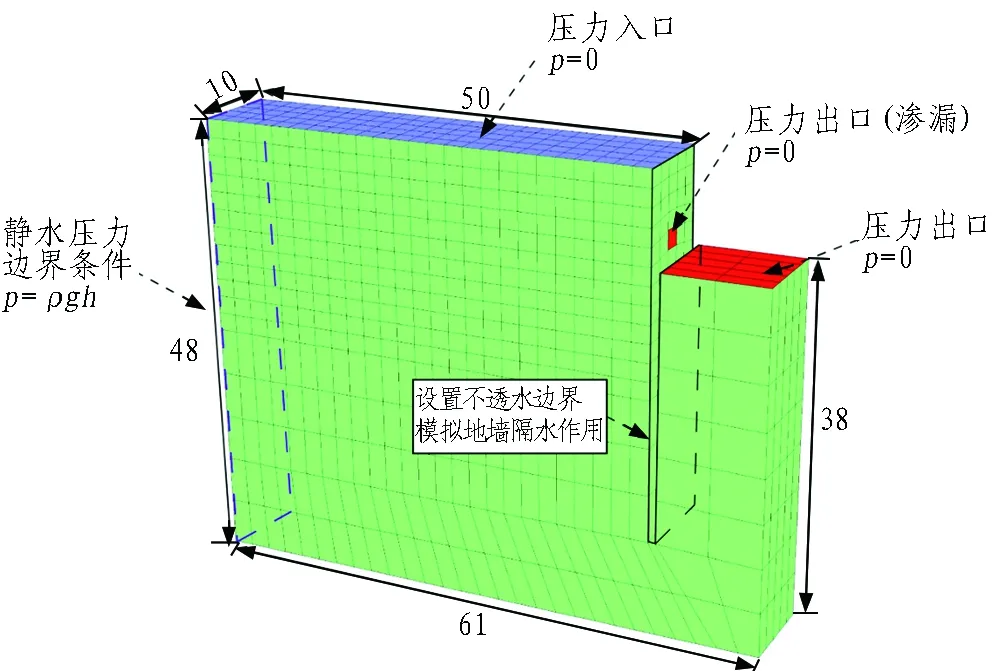
图8 CFD模型示意图(单位: m)Fig. 8 Schematic of CFD model (unit: m)

边界条件的设置主要分为3类。

1)压力入口边界。坑外流场顶面(蓝色)用于模拟潜水表面,设置其压强为0; 左侧边界(图中蓝色虚线框)压强假定为不受影响的静水压力条件,由于潜水是从无限远处补给,按照p=ρgh以用户自定义函数的方式设置边界压强。

2)压力出口边界。坑内顶面(红色)为降水后坑内的水位面,设置其压强为0; 结合前述DEM模型中的地墙缺口,在流场相应位置处设置尺寸相同的压力出口,并设置其压强为0,以模拟地下水渗漏的情况。

3)不透水边界。为模拟地墙的隔水作用,在地墙相应位置设置与地墙等宽的U型槽(图中黑色线框),并将槽壁设为不透水边界。

设置好边界条件后,开启重力选项并进行流场初始化并计算,即可得到流场的数值解。

2.3 模型验证

提取Fluent计算得出的流场单元节点、流速、压强等数据文件,将其导入PFC软件中,进行流-固耦合计算。通过PFC命令流set timestep auto,考虑当前模型刚度选取合适的时间步长进行耦合计算,计算过程中,时间步长在4.5×10-6上下变化。提取运算步数为1×104时基坑模型的横剖面如图9所示,采用CFD-DEM流-固耦合方法能够对渗漏过程中产生的土颗粒渗蚀现象进行模拟。

图9 地墙渗漏横剖面示意图(运算步数=1×104)Fig. 9 Cross-section of diaphragm wall leakage (time step of 1×104)

由于所依托实际工程空间与时间尺度跨度大,考虑到计算能力限制,难以将数值模型与实际工程在时间尺度上确定对应关系。因此,在各个位移发展关键节点(见图5),以最大地墙侧移值为参考指标,将计算数据与监测数据进行对照,得到对应的运算步数,如图10所示。需要注意的是,实际工况中,在关键节点0(2019年2月20日基坑开挖)以前,开展了基坑预降水试验,导致地墙产生了一定的开挖前侧向变形,而本数值模型仅模拟了正式开挖降水施工步骤,这导致关键节点0处实测值和计算值存在一定的差异。同时,相较于实测数据,数值模型在既有工况基础上,模拟了不加干预情况下的地墙侧移发展情况,以对富水砂性地层的地墙渗漏灾害演化全过程进行分析。

图10 数值模型验证Fig. 10 Validation of numerical model

3 分析讨论

3.1 渗漏影响空间特点

3.1.1 渗漏影响区域分析

1)颗粒当前速度与所处的位置关系能够反映渗漏过程中下一时刻的发展情况。提取计算步数为4×104时的DEM模型,截取计算模型中线(Y=5 m)两侧薄层颗粒,记录颗粒的位置坐标及对应的竖向速度分量,绘制速度云图,如图11所示。为方便观察分析,提取并记录竖向速度分量的最大值vmax(以向下为正,并对少量向上的速度赋较小正值),对每一个速度进行了ln(vmax/v)的数据处理,即速度云图中,颜色较深的区域代表该区域的颗粒有较大的竖向速度。通过分析可以发现,以渗漏中心为圆心,0.5HL(HL为渗漏中心埋深)为半径的扇形范围内(区域Ⅰ)和紧邻地墙后方槽型区域(区域Ⅱ)地层竖向沉降发展较快,这与地层受渗蚀影响后,渗漏中心局部土体损失,导致周围及上部土体失去支撑有关。

图11 颗粒竖向速度云图(运算步数=4×104)Fig. 11 Contour of vertical velocity of particles (time step of 4×104)

2)相较于颗粒速度云图,颗粒当前累积位移与初始位置的关系可以反映渗漏过程中的既有影响区域。提取计算步数为4×104时DEM模型的计算结果,截取计算模型中线(Y=5 m)两侧薄层颗粒,导出其竖向位移(以向下为正,并对少量向上的位移赋较小正值),同样,对每一个位移进行了ln(smax/s)的数据处理,并记录颗粒id,再根据颗粒id从流固耦合模拟起始状态提取对应颗粒的初始位置坐标,得到位移云图,如图12所示。图中颜色较深的位置,代表此处的颗粒在渗漏过程中发生了较大的竖向位移。总体上看,墙后土体可根据位移大小大致分为A和B 2个直角梯形区域,区域A地层受到渗漏影响,产生了较大的竖向位移,其中,A、B两区的分界线与水平面夹角近似为(45°+φ/2),分界线起始位置与渗漏引发的颗粒流失区域相接,这表明渗漏引发地层损失后,墙后土体沿着近似朗肯主动土压力破坏面发生位移。具体分析渗漏影响较大的区域A,与图11对应,区域Ⅰ和Ⅱ的土颗粒有较大的竖向位移。同时,区域Ⅰ以上的颗粒受到临时形成的土拱阻挡,位移发展不充分,导致区域Ⅰ局部出现位移极值,反映了地层空洞的形成。

图12 颗粒竖向位移云图(运算步数=4×104)Fig. 12 Contour of vertical displacement of particles (time step of 4×104)

3.1.2 地表沉降增量分析

为研究渗漏引起的地表沉降增量规律,设置无渗漏对照模型(即仅修复地墙缺口及渗流场渗漏出口,其他条件不变)并模拟计算。在提取坑外地表沉降计算值时,通过编程控制,沿坑外远离地墙方向,将分析点单位宽度范围内坑外地面表层的土体颗粒累计竖向位移进行提取,并作算术平均处理。然后,在相同关键节点(即计算模型中相同计算时步)下,将渗漏模型和无渗漏对照模型地表沉降做差,并对地墙距离进行针对渗漏(中心)深度的归一化处理,即得到如图13所示渗漏引起的地表沉降增量曲线。首先观察距离地墙范围为1倍渗漏深度的区域,地表沉降增量较大,且随着运算时间步的增加,沉降增量的增加较大,沉降发展迅速;而在1倍渗漏深度以外范围内,地表沉降虽有所发展,但相比前者沉降较小,且沉降发展缓慢,然而,仍需要关注处于该区域内的建筑和管线等。

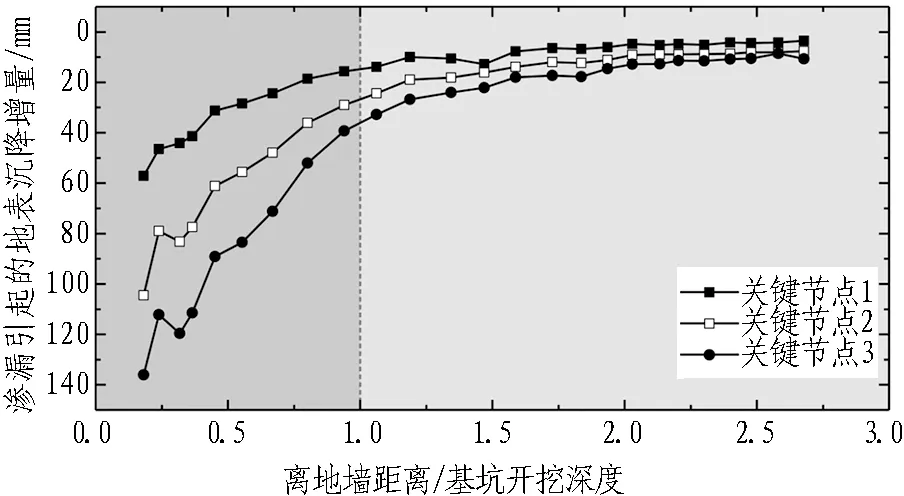
图13 渗漏引起的地表沉降增量-规范化离地墙距离关系Fig. 13 Variation of ground subsidence increment due to leakage with normalized-distance to diaphragm wall

3.2 渗漏影响时间特点

3.2.1 空洞发展规律分析

在DEM模型中,颗粒间接触力链是分析模型内部受力变化和运动细观机制的重要参考。截取地墙后 纵剖面附近颗粒,提取渗漏不同阶段的颗粒间接触力链图进行探讨,如图14所示(圆柱体的粗细代表颗粒间作用力大小)。

图14 颗粒间接触力链图Fig. 14 Force chain between particles

由图14分析可知:

1)渗漏初期,土体颗粒未发生明显移动,但在渗漏中心附近颗粒间接触力链开始断裂,表明此处颗粒将失去周围颗粒的约束,受动水力产生位移而流失。

2)随着渗漏的发展,断裂力链的范围扩大,土体内部中心开始出现空洞;空洞上方力链方向发生转变,形成类似拱形的分布形态,意味着空洞上方颗粒受力形式发生变化,拱效应的形成,暂时阻碍了浅层地层的下沉,也解释了空洞形成的原因。

3)渗漏中期,空洞尺寸扩大至一定程度后,无法继续维持拱效应,因此空洞上方力链出现断裂,空洞开始塌陷,地层位移的影响范围波及地表。

4)渗漏后期,土体流失严重,地层发生严重沉降;空洞持续塌陷,且由于土体颗粒不断随动水力涌出,中心处难以形成稳定力链。力链整体变粗现象也反映出,地层在坑内外水位差和动水力作用下发生沉降和压缩,造成各深度下土压力均有不同程度的增长。

为进一步探究渗漏过程中地层空洞的发展情况,提取不同计算时间步下,空洞周边颗粒的几何坐标,对空洞的横向、竖向跨度及几何面积进行统计,绘制折线如图15所示。通过分析可知: 土体内部空洞经历了生成—扩展—坍塌3阶段。随着土体渗漏的发展,土体内部空洞的横向、竖向跨度及几何面积均表现为先增大再减小;空洞尺寸在渗漏前期发展较快,在0～2×104步间曲线斜率较大,说明渗漏前期土体颗粒流失较快,空洞不断扩大;在2×104～4×104步间,空洞尺寸达到最大值,空洞上方土体开始加速下沉坍塌,不断填充空洞;4×104步以后,空洞尺寸不断减小,上方土体及地表沉降随之不断发展。

图15 空洞尺寸统计变化曲线Fig. 15 Variation of size of cavity with time step

3.2.2 地表沉降发展分析

统计各时步对应的地表最大沉降值,绘制如图16所示地表最大沉降值与运算时步对应关系曲线。由图可知,该关系曲线以5×104运算时步为界,分为2个线性段,结合3.2.1节中对空洞发展规律的总结,5×104运算步为空洞尺寸达到最大值,即将塌陷的时刻。通过对比2段曲线可以得出,空洞发展规律与地表沉降发展速度的变化存在较大相关性,在渗漏初期土体流失量较少的情况下,地表沉降发展较缓慢,此阶段由于土体内部存在土拱效应而形成地层空洞,减缓了浅层土层和地表的位移发展,地表最大沉降增长相对较平缓;当渗漏发展至中期,空洞尺寸扩展至无法维持的程度后塌陷,浅层土层随之下陷,引起地表位移快速增长,地表最大沉降增长迅速。

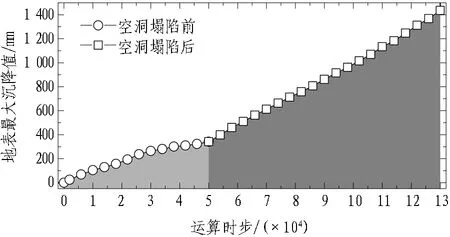
图16 地表最大沉降值-运算时步曲线Fig. 16 Variation of maximum ground settlement with time step

3.3 渗漏深度变参分析

为探究基坑地墙在不同深度发生渗漏时的影响规律,以图6所示基坑模型为基础,分别在开挖面处(Case1,HL=He,He为基坑开挖深度)、开挖面以上(Case2,HL=0.3He)、开挖面以下(Case3,HL=2He)设置地墙缺口模拟渗漏情况,对渗漏发生深度做变参分析,其中,Case1对应实际基坑渗漏事故。

3.3.1 水土合力变化分析

在DEM软件中设置测量球,使其竖向排列在地墙两侧,并保证测量球与地墙颗粒相切,再对同一埋深的测量值求算术平均,获取地墙两侧的水土压力合力,绘制地墙附近水土合力与地墙深度关系曲线,如图17所示。

图17 地墙附近水土合力曲线Fig. 17 Water and earth pressure near diaphragm wall

1)主动区方面。考虑富水砂性地层的特性,采用水土分算方法计算朗肯主动土压力,并绘制曲线。由此可以发现: 无渗漏情况下,地墙所受主动侧水土压力分布图和朗肯土压力的分布模式基本相同,吻合较好; 而考虑渗漏情况下,统计主动区水土合力最大值及所在深度,计算得到同等深度下,相较于无渗漏对照组,主动区水土压力合力分别增加了8.5(Case1)、7.0(Case2)和5.7倍(Case3),相关统计信息见表4。这表明,当渗漏发生在开挖面处或开挖面以上时,渗漏点直接与外界相通,渗漏处水和土失去原有支撑力而迅速向坑内流动,对地墙形成较大的水土压力;而当渗漏发生在开挖面以下时,渗漏点的产生仅是使坑内外水土相通,水土压力增长幅度较小。

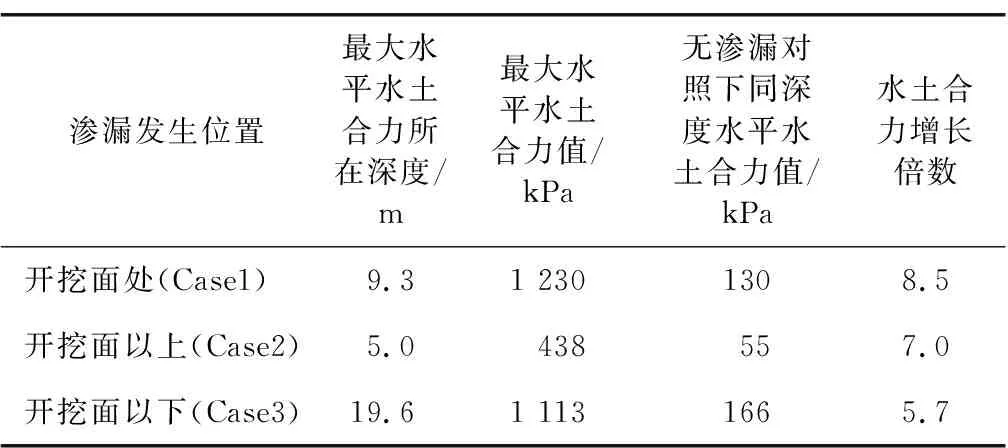
表4 主动区水土合力最大值统计Table 4 Statistics of maximum active water and earth pressure

2)被动区方面。考虑达到被动极限土压力所需的墙体位移量级约为0.01H(H为墙高),被动区一侧未达到极限平衡状态,因此并未绘制朗肯土压力曲线,观察图像可以发现,当渗漏发生在开挖面处(Case1)和开挖面以上(Case2)时,被动区水平水土合力变化与无渗漏情况相比并不大,这是因为渗漏处位于开挖面以上,水土渗漏仅对开挖面以上主动区应力水平造成影响,对开挖面以下渗流场及水土运动影响较小; 而当渗漏发生在开挖面以下(Case3)时,被动区水平水土合力与其他3种情况相比有一定程度的降低,这是由于渗漏点的存在缩短了基坑内外渗流路径,增大了坑内向上的渗流速度及动水力,导致被动区土体有效应力降低,被动水平土压力也随之降低。值得注意的是,渗漏点附近右上方水土压力出现小幅度增长,这是因为从渗漏点左侧流至坑内的地下水产生较大渗流力,导致渗漏点右侧小范围水土压力增长。

3.3.2 颗粒迁徙规律分析

如图18所示,追踪A—E 5个典型位置处的颗粒运动轨迹,探讨不同渗漏深度下的颗粒迁徙规律,颗粒运动轨迹如图19所示。

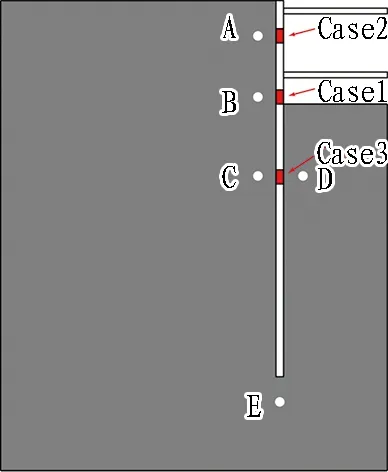
图18 颗粒轨迹追踪取点位置示意图Fig. 18 Schematic of traced particles′ initial positions

图19 不同渗漏深度下各点轨迹对比Fig. 19 Comparison of particles′ path in different cases

为了更直观地观察和对比各点间的轨迹长短,在同一渗漏深度条件下的轨迹比例尺相同;不同渗漏深度条件下,Case1与Case3比例尺相同,而Case2中单位长度所代表的实际轨迹长度是其余二者的4倍。通过分析可知,渗漏过程中,渗漏点上方的颗粒会产生竖向沉降,渗漏点附近的颗粒将产生沿动水力方向的大幅位移,渗漏点下方地层受到影响相对较小。

3.4 地墙渗漏风险辨识及防治措施

3.4.1 不同渗漏深度的风险辨识

富水砂性地层地质条件下,地墙难以完全阻隔基坑内外的水力联系,将形成由基坑外绕经地墙底部流向基坑内的渗流路径,基坑主动区受到向下的动水力,基坑被动区受到向上的动水力,由土体竖向应力变化带来的侧向压力差加剧了地墙向坑内方向的侧向变形;同时,该渗流场也对基坑的抗隆起及管涌安全性能提出了考验。由3.3节对渗漏深度的变参分析结果可知: 1)不同渗漏位置会伴随着相应的事故迹象,当其发生在开挖面处及开挖面以上时,主动区水土压力激增将导致渗漏位置附近土颗粒发生沿动水力方向的位移,地墙侧向位移大幅度迅速增长,带来地墙结构断裂以及坑外地表沉降突增的风险[4]。2)当渗漏发生在开挖面以下时,由于渗漏点上部地层失去稳定性会产生相应的竖向沉降,更深的渗漏点则意味着存在更大的地层影响范围,另一方面,虽然墙后主动区水平水土压力增长幅度不及上述二者,但仍需要关注渗漏引发的地下水渗流路径改变带来的风险: 当开挖面以下地墙出现渗漏点后,部分流体将直接从渗流点处流入坑内,渗流路径缩短导致动水力增大,且由于此时增大的动水力位于开挖面以下,地墙将有可能发生向坑内的踢脚破坏[4]。

3.4.2 地墙渗漏灾害防治措施

针对深厚富水砂性地层中深基坑地墙渗漏灾害问题,首要目标是预防渗漏事故灾害的发生。基坑渗漏的直接原因是围护结构出现裂缝或缺口,导致围护结构背后的土体和水侵入坑内。以地墙为例,发生渗漏的原因可能是混凝土振捣不均匀、接缝处未处理得当等导致地墙内部出现渗水通道,在地下水压力作用下不断被渗蚀扩展而引发基坑渗漏。因此,确保地墙施工质量是保证基坑稳定安全的关键。

1)加强对围护结构变形的监测,做到渗漏事故早发现。富水砂性地层中基坑工程一旦发生渗漏,灾害发展速率较快,通过实时监测地墙侧向位移发展,可以尽早发现渗漏事故。通常而言,当地墙侧向位移在某深度处突然出现大幅增加,大概率在该深度出现了墙体渗漏问题,此时应尽快采取有效堵漏措施。否则,一旦墙体渗漏引起的坑外地层空洞发生坍塌,会严重危及基坑本身和周边环境的安全。由3.2节分析得到的渗漏影响时间规律可知,堵漏抢险的最佳阶段为渗漏前期,此时水土流失量和坑外地表沉降尚不严重,较易控制和修复,但如果渗漏发展至中期或后期,空洞塌陷,地面大幅沉降,将难以补救,后果不堪设想。因此,应对基坑渗漏事故重在及时,尽可能在渗漏发生早期将险情控制住,使事故影响和造成的损失降到最低。

2)渗漏发生后,通常采用反压砂袋等措施快速封堵渗漏位置,阻断土体颗粒流失路径;此外,在墙后一定范围内注浆封堵渗漏通道并填充内部空洞,注浆深度范围应在地墙侧移突增所在深度附近,且距离墙后0.5倍渗漏深度范围内,应在临时形成的应力拱破坏之前完成空洞填充,避免临界空洞塌陷后产生突沉灾害; 可架设临时支撑,控制围护结构在动水力作用下的侧向变形发展。

3)面对可能出现的渗漏问题,应对事故潜在影响区内的敏感建(构)筑物提前采取预防措施,尤其是1倍开挖深度范围内的建(构)筑物,可采取如地基注浆加固、基础托换、建筑物上部结构加固等方法。

4 结论与建议

基于CFD-DEM流-固耦合方法,结合实际工程渗漏事故,对富水砂性地层中地墙渗漏诱发地层塌陷灾害的细观机制进行了探讨,主要结论如下:

1)渗漏发生后,以渗漏中心为圆心,0.5HL为半径的扇形区域和紧邻地墙槽型区域内颗粒发生向渗漏中心的渗蚀,由此造成的渗漏影响区的边界与水平面夹角近似为(45°+φ/2);由渗漏引发的地表沉降增量在地墙后1倍渗漏深度范围内量值较大,发展较快,需重点关注。

2)渗漏过程中,空洞的出现与土体颗粒间接触力方向的转变相关;地层内部的空洞经历了生成—扩展—坍塌3阶段,空洞的坍塌伴随着地表沉降的加速发展。

3)地墙渗漏会引起渗漏中心附近水土合力突增5.7～8.5倍,以渗漏位于开挖面处增幅最大,位于开挖面以下增幅最小;渗漏中心附近土体颗粒将沿动水力方向发生大幅位移,渗漏上方土体将产生竖向沉降,渗漏下方土体受到影响较小。

后续可进一步基于数值模型分析地层颗粒级配及具体防治措施方案对灾害细观机制的影响,以期为工程防灾减灾提供参考。