基于拉格朗日插值的无网格直接配点法和稳定配点法1)

胡明皓 王莉华

(同济大学航空航天与力学学院,上海 200092)

无网格法[1-6]由于不需要划分网格,不存在网格类方法在求解大变形问题时容易出现的网格畸变问题,而且具有精度高、收敛率高等优点,近年来受到越来越多的关注,广泛应用于高速冲击、爆炸等复杂问题.常用的无网格法主要分为两类: 伽辽金型和配点型.由于进行区域积分,伽辽金型无网格法具有较好的精度和稳定性,然而其缺点是计算效率比较低.配点型无网格法通常更加简单高效[7-11],而且在一些简单问题中可以获得较好精度[12],但是对于一些复杂问题,其精度和稳定性明显降低.Zhang 等[13-14]提出最小二乘配点法(least squares collocation method,LSCM),通过采用比源点个数更多的配点来构建超定离散方程进行计算,显著提升计算精度和稳定性,然而超定方程求解也大幅降低计算效率.分区配点法[15-17]通过将区域分成若干个子域,提高了计算效率,而且降低了离散矩阵的条件数,提高了结果的稳定性,但是这种方法也是基于最小二乘求解,无法避免超定方程计算的缺点.最近,Wang 等[18-20]提出一种基于重构核近似(reproducing kernel,RK)的稳定配点法(stabilized collocation method,SCM),这种方法将问题域划分为若干个规则子域,对强形式方程在子域内进行积分,由于满足积分约束,可以实现精确积分.该方法提高了无网格法计算结果的精度和稳定性.由于积分效率高,该方法仍然保持配点型无网格法的高效特性.

常用的无网格法采用的形函数通常都是有理式,不具有插值特性,难以像有限元法(finite element method,FEM)一样方便准确地施加本质边界条件.这个问题也是目前无网格法的研究热点之一.在无网格方法中常见的处理本质边界条件的方法有拉格朗日乘子法[21]、罚函数法[22]和一些修正的方法[23-24].然而拉格朗日乘子法会增加未知数的数量,导致刚度矩阵不对称,从而增加了计算难度.罚函数法虽可得到对称的刚度矩阵,但其计算精度往往取决于罚参数的选取.另一些学者努力尝试将有限元法与无网格法相结合来施加边界条件.基于强形式配点法和有限元的单元,Gao 等[25]提出单元微分法(element differential method,EDM),之后改进等参单元的构建形式,可以由配点和相邻节点构建,提出自由单元配点法(free element collocation method,FECM)[26-27].在此基础上进一步弱化单元,提出有限线法(finite line method,FLM)[28],这种方法在求解低维和高维问题时均只需要在一个方向上构建单元,降低了单元畸变的可能性.这几种方法都是基于直接配点法,求解比较简便,虽然可以利用有限元单元的优势方便地施加本质边界条件,但是没能避免直接配点法的缺点和完全消除有限元单元畸变的可能性.

为了结合无网格法无单元畸变的优势和有限元法能方便施加本质边界条件的特点,Wang 等[29]在稳定配点法的基础上提出一种基于拉格朗日插值的稳定配点法,称为拉格朗日插值稳定配点法(stabilized Lagrange interpolation collocation method,SLICM).这种方法继承了稳定配点法精度高和稳定性好的优势,能够实现精确积分,同时由于拉格朗日插值形函数具有Kronecker delta 性质,可以像有限元法一样简便准确地直接施加本质边界条件.Wang等[29]考虑了均匀离散点和对应结构化网格的非均匀离散点的离散布置方案,并没有详细讨论离散点任意布置的情形.本文通过引入曲线拉格朗日插值形函数,实现了基于拉格朗日插值的直接配点法和稳定配点法的任意离散,进一步提升了这两种方法的适用范围.

1 拉格朗日插值近似

1.1 拉格朗日插值形函数

将一个一维区域离散为若干个离散点,基于其中部分离散点x1,x2,···,xi,···,xm(这一组离散点也可称为节点),一维拉格朗日插值多项式可表示为

其中m表示离散点个数.对于所有的i≠I,NI(xI)在x=xi处结果为0,当x=xI时,NI(xI)=1.因此,拉格朗日插值具有Kronecker delta 性质,可以表示为以下形式

图1 和图2 展示了一维2 节点和3 节点拉格朗日插值形函数中节点分布情况.二维和三维形函数可以通过一维形函数在不同方向上的张量积表示为如下形式

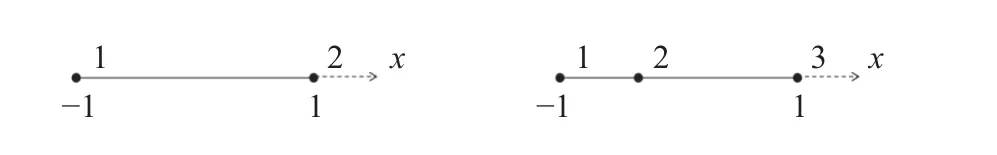
图1 一维2 节点和3 节点拉格朗日插值形函数的节点分布图Fig.1 Node distributions of the 1D 2-node and 3-node Lagrange interpolation shape functions

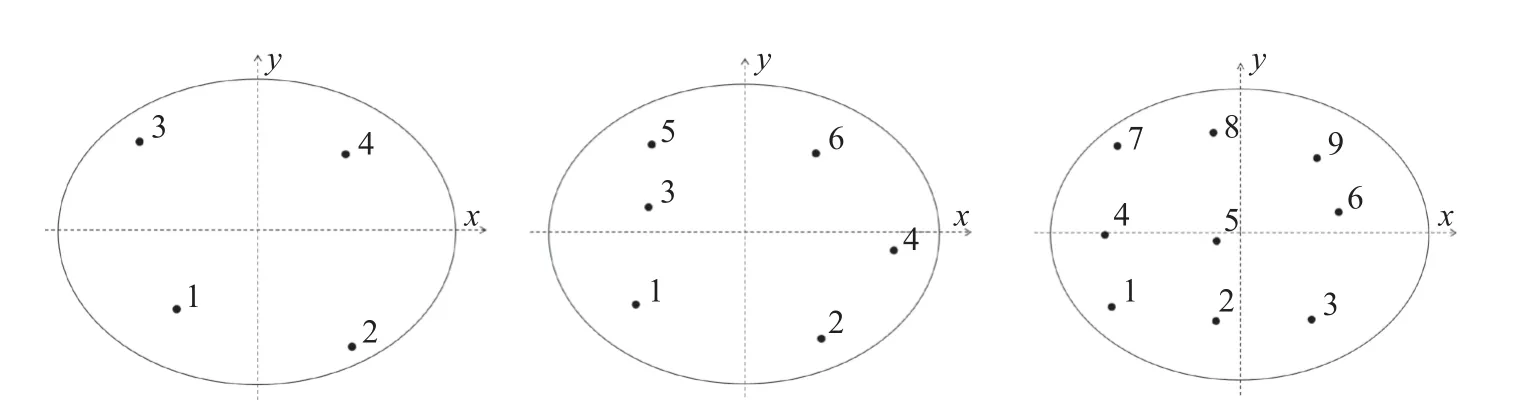
图2 二维4 节点、6 节点和9 节点拉格朗日插值形函数的节点分布图Fig.2 Node distributions of the 2D 4-node,6-node and 9-node Lagrange interpolation shape functions

对于二维问题x=(x,y),三维问题x=(x,y,z),下标L由下标I ,J和K的顺序排列确定.二维情况下4 节点、6 节点和9 节点拉格朗日形函数中节点分布如图2 所示.

图3～图5 展示了不同阶数下的拉格朗日插值形函数及其导数,其中p表示拉格朗日插值形函数的阶数.对于一维问题p=m-1,二维问题p=min{(m1-1),(m2-1)},三维问题p=min{(m1-1),(m2-1),(m3-1)}.

图3 p=2 时一维拉格朗日插值形函数Fig.3 1D Lagrange interpolation shape function when p=2

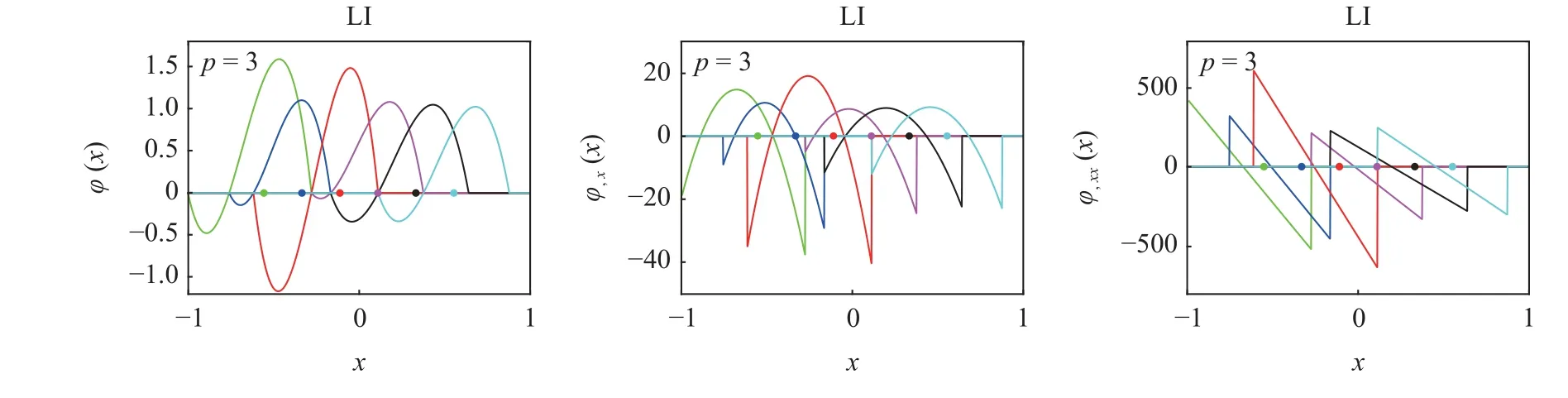
图4 p=3 时一维拉格朗日插值形函数Fig.4 1D Lagrange interpolation shape function when p=3

1.2 拉格朗日插值形函数的导数

一维拉格朗日插值形函数的一阶导数和二阶导数可以表示为以下形式

二维形函数的一阶和二阶导数也可以通过一维形状函数的张量积得到,可以表示为

同理,三维形函数的导数可表示为

1.3 拉格朗日插值近似

式(10)也可写成如下形式

2 直接配点法(direct collocation method,DCM)

边值问题可以表示为以下的一般形式

其中 Ω 表示待求问题的开区域,Γ 表示诺伊曼边界,Π 表示狄利克雷边界,整体求解区域=Ω∪Γ ∪Π.A,Bh和 Bg分别表示区域 Ω,Γ 和 Π 上的微分算子.u是未知量,f,h和g为对应的源项.

未知变量u可采用拉格朗日插值近似表示为

于是可以得到

将近似函数式(17)代入方程(14)～(16),并使其在域内和边界上满足配点方程,可以得到如下离散形式

在直接配点法中,配点的位置与源点位置相同且数量一致.当采用拉格朗日插值作为形函数时,该方法被称为拉格朗日插值配点法(Lagrange interpolation collocation method,LICM).系数矩阵a可以通过求解离散方程式(21)～式(23)来确定.离散方程式(21)～式(23)可改写为以下的矩阵形式

式中子矩阵为

3 稳定配点法(stabilized collocation method,SCM)

如图6 所示,在稳定配点法中,将域内和边界上布置若干个离散点,以该离散点为中心构建子域Ωl/Πl/Γl.子域的大小对于每个点可以是不同的,但为了简单起见一般使用相同大小的子域.子域的形状对于二维问题一般选择正方形,三维问题选择立方体即可.

图6 稳定配点法中点的布置图Fig.6 Points allocation in SCM

在稳定配点法中,对方程式(14)～式(16)的强形式在相应子域内进行积分,得到如下积分形式

将近似函数式(17)代入方程式(27)～式(29)可以得到

其中,p,q和r分别表示域内、诺伊曼边界和狄利克雷边界上的离散点.采用拉格朗日插值作为形函数的稳定配点法称为拉格朗日插值稳定配点法(stabilized Lagrange interpolation collocation method,SLICM).同时对方程式(30)～式(32)等式两边做数值积分可得

其中,ω表示积分点个数,wi表示积分权重,()l,()l和 ()l分别表示离散点pl ,ql和rl对应子区域内的积分点.通常可以使用高斯积分进行数值积分运算.式(33)～式(35)可以用矩阵形式表示如下

4 数值算例

本节采用一维、二维和三维3 个算例来评估基于拉格朗日插值的无网格直接配点法和稳定配点法的精度和稳定性.拉格朗日插值形函数的阶数与影响域内源点个数有对应关系,3 个算例均采用二阶形函数,其影响域均为二阶形函数所对应的影响域范围,即p阶形函数在单个方向上对应p+1个源点.根据文献[18]的研究结论,积分域大小和特征节点间距相距较近时,可以得到比较高的精度.因此,本文算例中的积分域大小均参照特征节点间距.

4.1 一维直杆问题

考虑如图7 所示左端固支的一维直杆的二阶微分方程问题,其控制方程为

图7 一维直杆示意图Fig.7 Description of the 1D rod problem

其中EA=1,L=1,f(x)=3x2,解析解为.

图8 为随机布点的一维直杆离散图,源点和配点布置在相同位置.图9 展示了拉格朗日插值配点法、拉格朗日插值稳定配点法和传统重构核近似配点法(reproducing kernel collocation method,RKCM)[30]在一维直杆问题中的数值计算结果和相应的误差,结果表明基于拉格朗日插值方法(LICM和SLICM)的求解精度明显优于基于重构核近似方法(RKCM)的求解精度,拉格朗日插值稳定配点法相比拉格朗日插值配点法有更好的计算精度,图10的收敛性分析更清晰地展示了这一结论(图标中的数字为收敛率).由于源点和配点均随机布置,收敛率和理论值略有差距,理论收敛率可参考文献[29].图11 比较了3 种方法的刚度矩阵条件数,可以看出稳定配点法的矩阵条件数更低,可以获得更好的稳定性.

图8 一维直杆问题源点离散图Fig.8 Discrete points of source points for the 1D rod problem

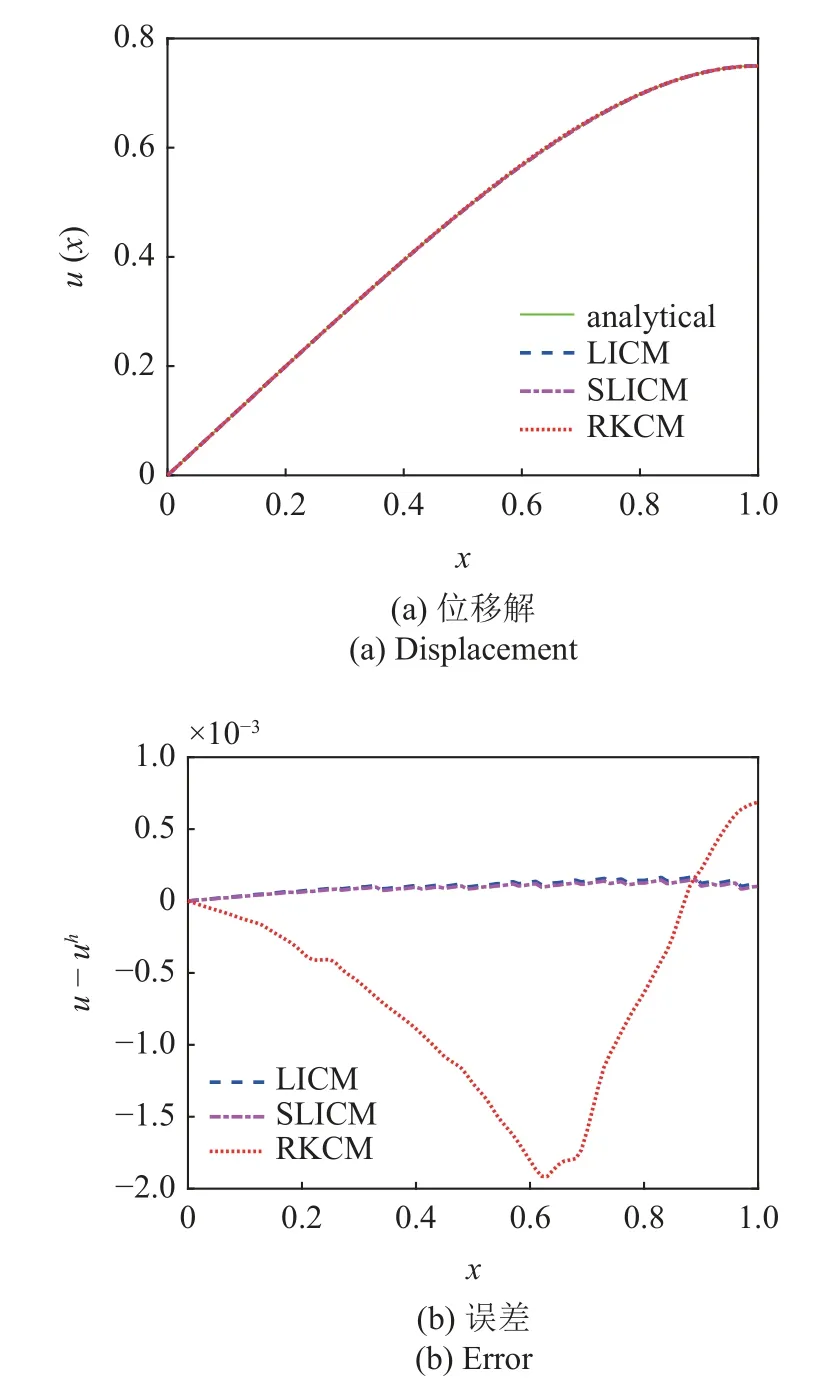
图9 一维直杆问题计算结果及误差Fig.9 Numerical solutions for the 1D rod problem

图10 一维直杆问题收敛性分析Fig.10 Convergence comparisons for the 1D rod problem

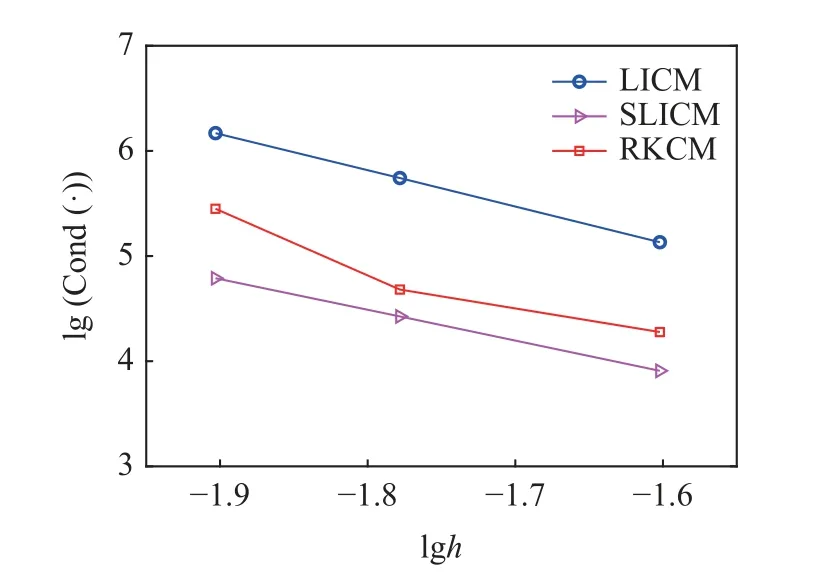
图11 一维直杆问题刚度矩阵条件数Fig.11 Condition number comparisons for the 1D rod problem

4.2 二维泊松问题

考虑二维空间中的泊松问题,控制方程和边界条件如下

其中 Ω=(-1,1)×(-1,1),解析解为u(x,y)=exy.文献[29]中研究了均匀离散和对应结构化网格布点的两种离散方式,本文讨论如图12 所示任意非均匀离散模式.源点和配点布置在相同位置.

图12 二维泊松问题源点离散图Fig.12 Discrete points of source points for the 2D Poisson problem

图13 和图14 分别展示了采用拉格朗日插值配点法和拉格朗日插值稳定配点法在域内和边界上的计算精度,边界计算结果达到了计算机精度,表明这两种方法都能够准确地施加本质边界条件.结合图15的收敛性分析可以看出稳定配点法对于离散点非均匀分布的二维泊松问题也能获得更高的精度.图16比较了两种方法的刚度矩阵条件数,稳定配点法的条件数更小,表示该方法具有更好的稳定性.

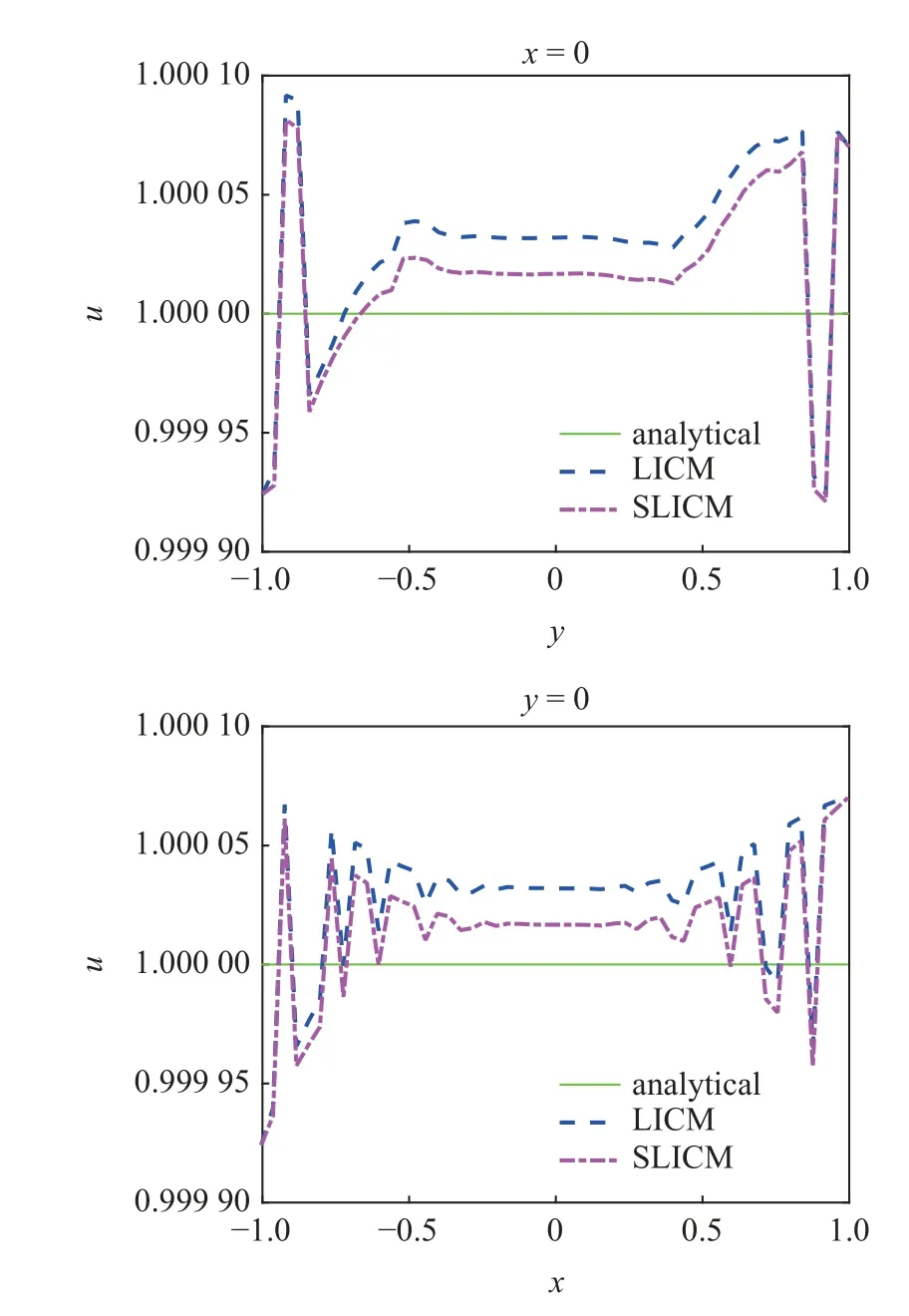
图13 二维泊松问题域内位移解Fig.13 Numerical solutions for the 2D Poisson problem

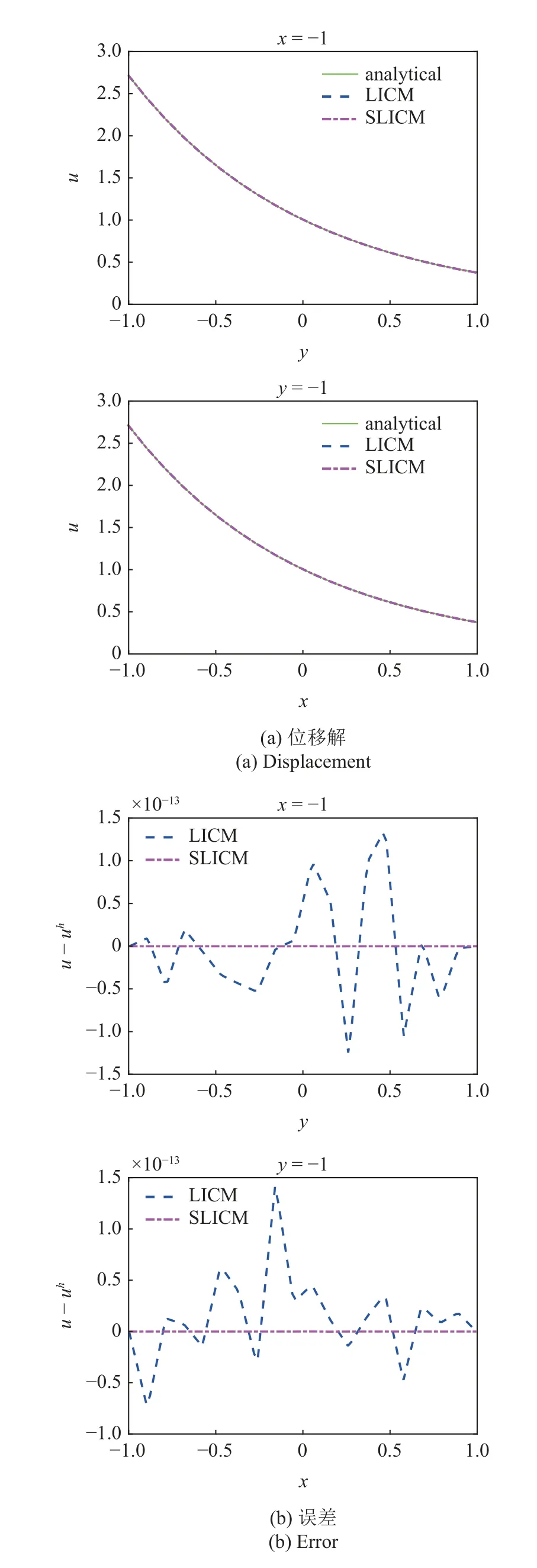
图14 二维泊松问题边界位移解Fig.14 Numerical solutions of boundary for the 2D Poisson problem

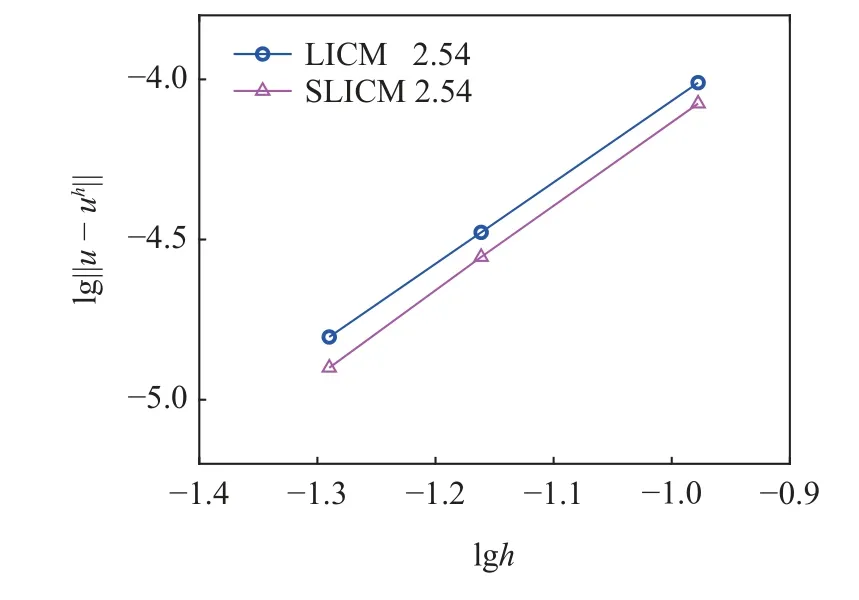
图15 二维泊松问题收敛性分析Fig.15 Convergence comparisons for the 2D Poisson problem

图16 二维泊松问题刚度矩阵条件数Fig.16 Condition number comparisons for the 2D Poisson problem

4.3 三维亥姆霍兹问题

考虑三维空间下亥姆霍兹方程,表示如下

其中 Ω=[-1,1]×[-1,1]×[-1,1],k=1,解析解为u(x,y,z)=sinx+siny+sinz.

将两种方法进一步扩展至三维空间计算上述亥姆霍兹方程,可以得到类似的计算结果.图17 展示了三维空间下的离散点布置图,图18 给出了域内x=0上的计算结果.图19 展示三维空间下的边界计算结果,可以看出两种方法对于边界的计算精度都非常好.图20 和图21 分别展示直接配点法和稳定配点法在三维亥姆霍兹问题上的收敛性分析和矩阵条件数分析.如前面两个算例得到的结论相同,稳定配点法有更好的精度和稳定性.

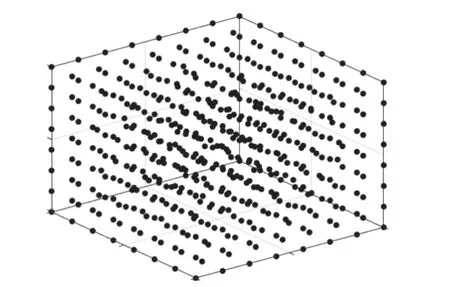
图17 三维亥姆霍兹问题源点离散图Fig.17 Discrete points of source points for the 3D Helmholtz problem

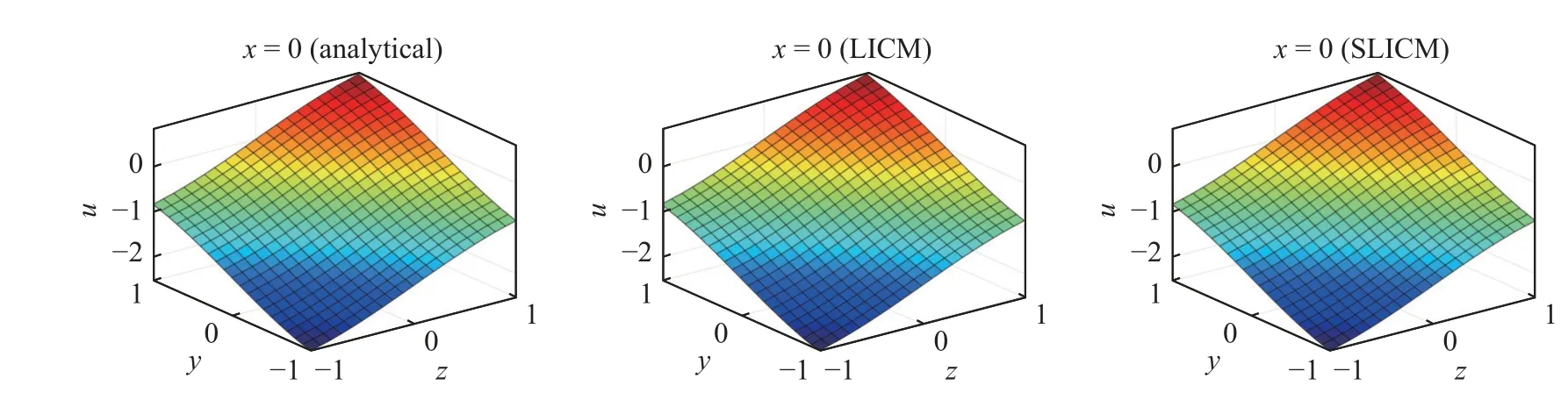
图18 三维亥姆霍兹问题域内位移解Fig.18 Numerical solutions of the inner domain for the 3D Helmholtz problem

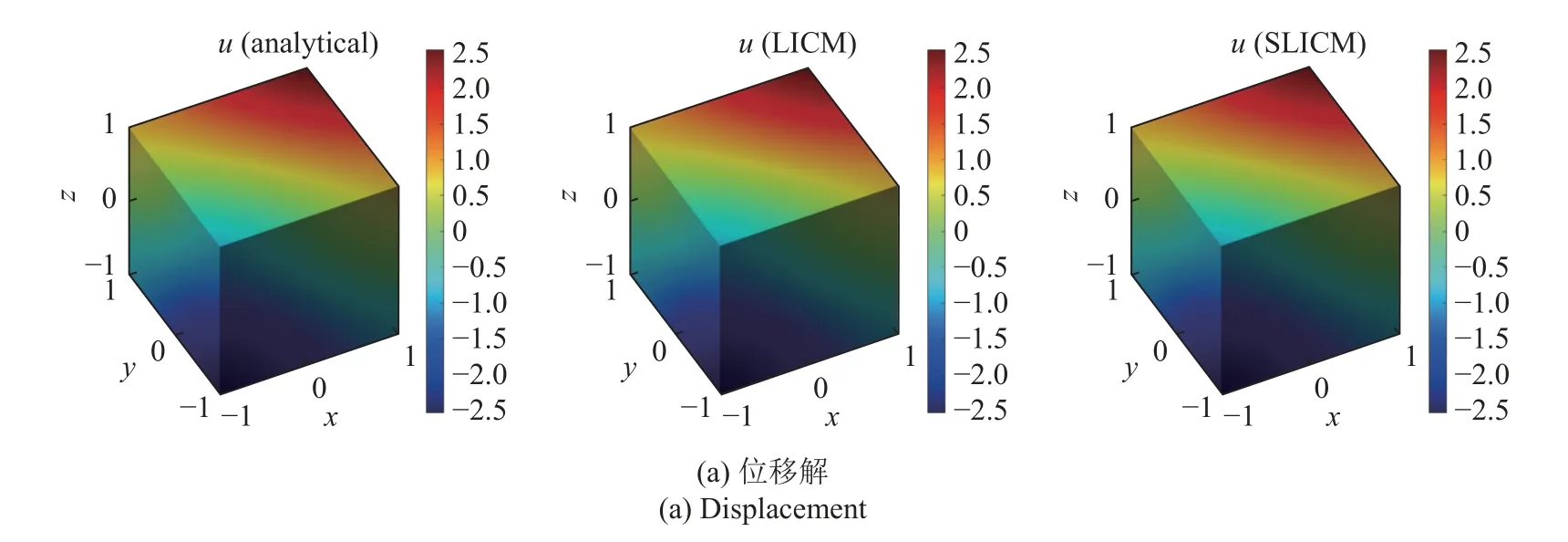
图19 三维亥姆霍兹问题边界位移解Fig.19 Numerical solutions of boundary for the 3D Helmholtz problem

图19 三维亥姆霍兹问题边界位移解 (续)Fig.19 Numerical solutions of boundary for the 3D Helmholtz problem (continued)

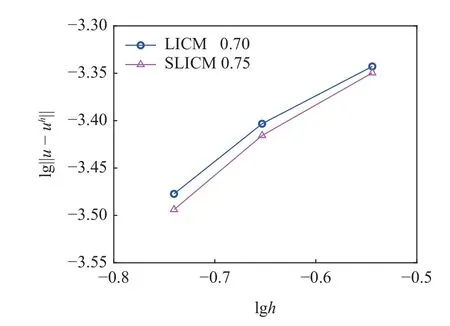
图20 三维亥姆霍兹问题收敛性分析Fig.20 Convergence comparisons for the 3D Helmholtz problem

图21 三维亥姆霍兹问题刚度矩阵条件数Fig.21 Condition number comparisons for the 3D Helmholtz problem

5 总结

本文将曲线拉格朗日插值多项式引入无网格直接配点法和稳定配点法中,构建了离散点可任意布置的拉格朗日插值配点法和拉格朗日插值稳定配点法.这两种方法的形函数与有限元法一样具有Kronecker delta 性质,能够简单准确地施加本质边界条件,相比较传统无网格方法在边界处理方面有较大优势,提升了无网格法在边界上的求解精度.拉格朗日插值稳定配点法将问题域划分为若干个子域,在子域内能够实现精确积分,积分降低了刚度矩阵的条件数,进一步提高了算法的精度和稳定性,解决了传统无网格法难以实现精确积分的难题.该两种方法由于采用曲线拉格朗日插值,离散点可任意布置,不再局限于结构化网格布点,使得这两种方法可以适用于各类复杂区域问题的求解.基于拉格朗日插值的直接配点法和稳定配点法的计算成本都比较低,边界求解精度高,稳定配点法可以通过精确积分进一步提高精度和稳定性,未来可以将这两种方法应用于更多力学问题和实际工程问题的数值分析.