渗流力对裸眼井筒周围应力场及地层破裂压力影响机理研究1)

王海洋 周德胜 黄 海 李 鸣

* (西安石油大学石油工程学院,西安 710065)

† (西安石油大学陕西省油气田特种增产技术重点实验室,西安 710065)

** (中国石油长庆油田分公司油气工艺研究院,西安 710016)

引言

在石油与天然气工程领域,通过井筒向储层注入工作液是注入井测试、二氧化碳封存和水力压裂的一个常见且必须的过程[1-2].注入的工作液作用于储层岩石改变了井筒周围的局部应力状态,并影响了岩石的变形和破坏[3-4].研究注入流体引起的应力场对于分析水力裂缝起裂与扩展机理、评价井眼稳定性和提高完井质量至关重要.

渗流力在土力学中又被称为渗透力,土力学教材将单位体积土体内土骨架受到的孔隙水的渗流作用力定义为渗流力[5-8].微观角度上渗流力就是渗透水流对土颗粒施加的水压力和拖曳力作用,宏观角度上渗流力就是流体渗流时对土骨架施加的一种等效体积力[9-14].国内外已有许多学者针对渗流力对岩土破坏的影响展开实验与数值模拟研究.Mourgues等[15-16]利用砂箱模拟实验验证孔隙压力梯度作用会产生渗流力,而且研究发现储层局部超压源作用下渗流力会改变储层的有效应力场,对储层构造产生显著影响.Rozhko 等[17-19]基于Biot 三维固结理论分析孔隙压力梯度作用下,渗流力对岩石破坏模式和临界破坏压力的影响,其研究发现渗流力作用可能会触发储层微地震.Cobbold 等[20-21]基于砂箱模拟实验研究发现渗流力作用可能会导致储层岩石产生断层和纤维状层理.Zeng 等[22]分析饱和与非饱和渗流条件下水合物多孔介质中渗流力的作用机理,其研究发现渗流力会直接影响水合物的力学行为.Pan等[23]分析渗流力作用下三维边坡的稳定性,其研究发现渗流力作用对边坡失稳有显著影响.周科平等[24]研究发现渗流力对多孔介质的力学特性有显著影响,随着渗流力增大多孔介质的破坏模式变得更加复杂.尽管上述研究已经表明渗流力对土体、岩石和水合物等多孔介质的变形和破坏有着重要影响,但在石油与天然气工程领域渗流力尚未引起足够的重视,有关渗流力的研究报道仍然很少.

水力压裂技术作为目前国内外开发非常规储层最为关键的提采技术,被广泛应用于各大油气田[25].压裂过程中,高压作用下压裂液会渗流进入储层岩石形成孔隙压力梯度,渗流的流体会对岩石骨架施加以渗流力从而影响裂缝起裂扩展过程[26].为求解方便,此前针对水力压裂裂缝起裂扩展的数值研究通常认为储层不可渗透,没有考虑压裂液施加给岩石骨架的渗流力作用[27-31].然而已有大量水力压裂实验研究表明,低黏度压裂液渗流进入储层不仅降低了地层破裂压力[32-35],而且有利于激活并沟通天然裂缝与层理形成更复杂的裂缝网络[36-38].但渗流作用如何影响水力压裂裂缝起裂与扩展过程,渗流力对裂缝起裂压力和扩展轨迹的作用机制仍然不清楚,因此需要开展更深层次的数值研究.

本工作基于Biot 固结理论分析压裂液渗流进入储层岩石时渗流力的作用机理,以裸眼井为例推导了渗流力作用形成的应力场解析解和考虑渗流力作用的地层破裂压力解析解公式,研究渗流力作用对裸眼井地层破裂压力的影响规律,以期为非常规储层水力压裂开发提供理论支撑.

1 渗流力宏观量级分析

当流体流经岩石孔隙或者土体时,渗流的流体会对岩土颗粒表面施加拖曳力与法向水压力,土力学教材将流动流体对单位体积岩土颗粒施加的渗流作用力定义为渗流力[5-8].为克服渗流力的反作用力,流动流体产生了压力损失,形成了水力梯度.实际上在油气田开发过程中,各种工作液在岩石孔隙喉道流动时同样会产生水力梯度,渗流的工作液会对岩石骨架施加体积力即渗流力的作用.根据丁洲祥[9]提出的广义渗流力宏观定义式,本节对渗流力的宏观数量级进行了初步的研究

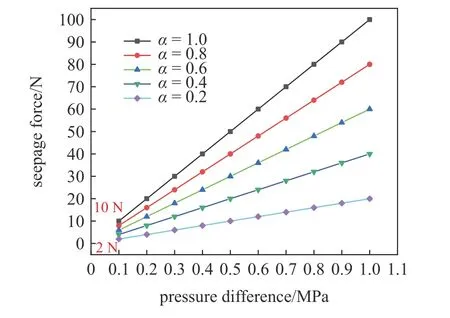
图1 1 cm3 岩样在不同压差和Biot 有效应力系数下所受渗流力大小Fig.1 Seepage force of 1 cm3 rock sample under different pressure differences and Biot effective stress coefficients

对于岩石密度等于4.5 g/cm3的岩样,1 cm3大小的岩样所受体积力重力的大小等于0.045 N.然而从图1 可以看出,对于1 cm3大小的岩样,即使孔隙压差很小等于一个大气压0.1 MPa 时,体积力渗流力的大小最大(α=1)可达到10 N,远远超过了同等大小岩样所受体积力重力的大小;即使岩石的Biot有效应力系数很小等于0.2 时,其在0.1 MPa 孔隙压差作用下,渗流力的大小也可达到2 N,同样远超岩样所受的重力.当孔隙压差达到1 MPa 时,1 cm3大小的岩样所受渗流力最大可达100 N,其作用完全是不可忽略的.随着孔隙压差的增大,不同Biot 有效应力系数下,岩样所受渗流力大小的差距越来越大.在相同孔隙压差下,岩石Biot 有效应力系数越大时,渗流力的作用越强.

2 渗流力对井筒周围应力场影响机理研究

2.1 渗流力对储层岩石作用机理分析

由于土体和岩石的物理性质与力学性质差异很大,土力学渗流力的宏观定义式无法直接应用于岩石力学线弹性变形理论.基于此,本文基于经典的Biot 三维孔隙固结理论分析了渗流力对岩石的作用.Biot[39]通过分析孔隙水压强对岩石单元体线弹性变形的影响,推导了包含孔隙水压强作用的有效应力平衡微分方程和应力边界条件

从方程(2)和方程(3)可以看出,当没有外部载荷仅有流体作用于岩石时,岩石骨架受力由两部分组成: (1)流动流体对岩石单元体施加的渗流力作用以体积力(-α∂P/∂x,-α∂P/∂y,-α∂P/∂z)的形式作用于岩石;(2)流体作用于岩石表面的法向水压力(αPl+Px;αPm+Py;αPn+Pz)以面力形式作用于岩石边界面.流体施加给岩石单元体的面力和体积力作用将共同决定流体单独作用于岩石所形成的有效应力场.

Biot 有效应力系数α的物理意义可代表孔隙压力抵消围压去产生体积应变的效率,该系数控制着方程(2)中渗流力作用的大小.Biot 有效应力系数通常满足 φ≤α≤1,其中φ为岩石的孔隙度[40-41],该系数可以根据Wu 等[42]提出的方法测量获取.当α取极限值1 时,方程(3)中面力项会消失,流体仅施加渗流力于岩石单元体;在一些工程情况下为计算方便,α往往取极值0,此时孔隙流体压力对单元体的形变没有影响,岩石可视为完全不可渗透的,此时方程(2)中体积力项消失,流体作用仅有面力项的作用.

2.2 井筒周围流体作用形成的应力场分析

在石油工程领域,对井筒周围应力场进行分析一直是研究的重点,井筒周围的有效周向应力场直接决定水力压裂裂缝起裂过程与钻井工作液安全窗口的设计.在压裂过程中,井筒压力会达到几十兆帕,压裂液会在高压作用下渗流进入井筒周围储层的岩石,从而对岩石骨架施加以渗流力作用.然而以往研究都未能将渗流力作用进行剥离,渗流力对井筒周围有效应力场和破裂压力的影响机理仍然不明确.基于此,本文建立了如图2(a)所示的井筒横截面物理模型,结合上一节建立的理论力学模型去分析井筒周围流体渗流作用下渗流力项和面力项作用形成的应力场.如图2(a)所示,假设岩石各项均质同性,流体沿着径向进行渗流,井筒内压为Pw,外边界储层初始孔隙压力为Po,井筒内半径为a,外半径为c,r为距离井轴的距离,θ为角度.通过建立极坐标系来分析井筒周围流体作用形成的有效径向应力和有效周向应力(注意本节设压应力为正值).

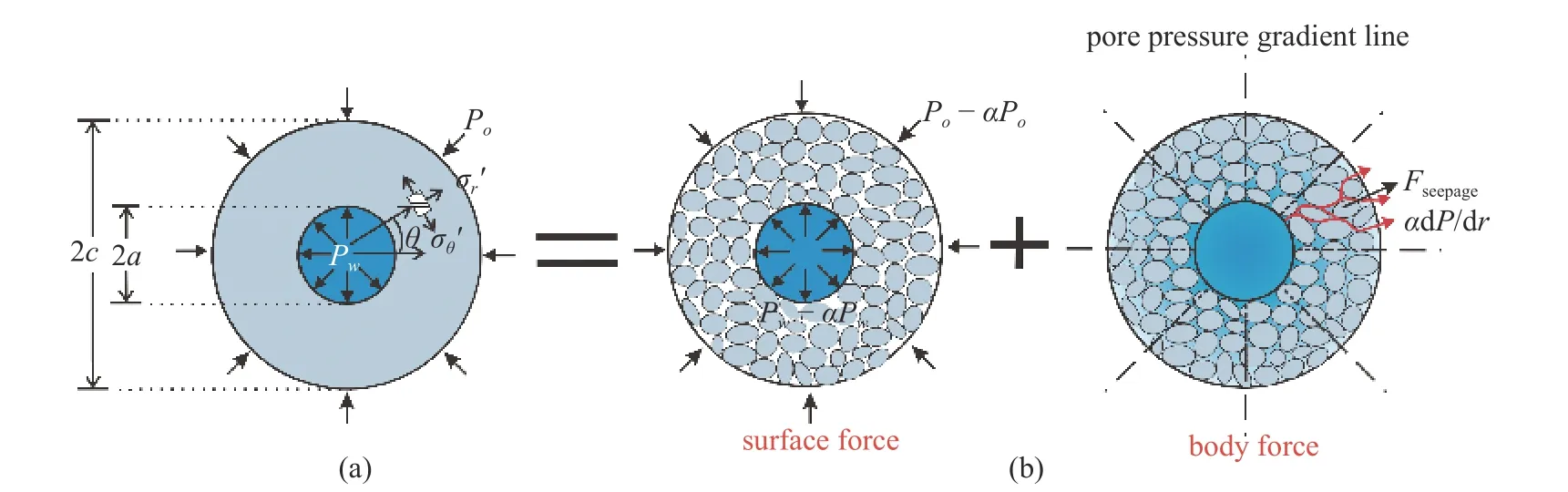
图2 流体作用下裸眼井筒周围岩石受力示意图Fig.2 Schematic diagram of the force on the rock around the open hole wellbore under the action of fluid

首先根据2.1 节的理论力学模型分析流体稳态渗流时,井筒周围储层岩石满足的平衡方程和边界条件,将方程(2)和方程(3)在极坐标系下转换可得到

方程(4)和方程(5)即为流体单独作用于井筒周围储层岩石时满足的应力平衡方程和应力边界条件,从方程(4)和方程(5)可看出流体作用于井筒周围储层岩石形成的有效应力可拆解为体积力项和面力项所形成的有效应力场的叠加(图2(b)所示),具体包括: (1)流体施加给井筒内外边界的面力,即径向水压力Pw-αPw和Po-αPo;(2)渗流进入储层的流体施加给岩石骨架的径向体积力,即渗流力αdP/dr.

通过经典弹性力学拉梅公式[43],可以直接得到井筒内外边界面力项(方程(5))形成的有效周向应力

其中P1=Pw-αPw;P2=Po-αPo.当储层完全不可渗透时,Biot 有效应力系数α=0,此时渗流力项αdP/dr消失,仅剩下井筒内外边界的面力项,则公式(6)就转化为了岩石不可渗透条件下,井筒周围水压力作用于井筒内外边界所形成的周向应力公式

根据Terzaghi 有效应力定律[43]进一步可得,储层不可渗透,不考虑流体渗流时,流体作用于井筒周围形成的有效周向应力

为了求解井筒周围渗流力形成的应力场,首先对方程(4)进行处理,由于流体沿着径向渗流,渗流力α∂P/∂r分布是轴对称的,所以有效应力分布必然是轴对称的,因此应力分量和以及应变ɛr和ɛθ都只是r的函数且剪应力为0,所以求解渗流力作用形成的有效应力场时平衡微分方程(4)可被化简为

为了得到渗流力αdP/dr在井筒周围形成的周向应力,必须要分析井筒周围的孔隙压力分布,为此引入Wang 等[44]推导的井筒周围流体稳态渗流时的孔隙压力分布公式

令边界处径向压应力为0,基于弹性力学方法联立求解方程(9)和方程(10)(附录A),可以推导得到渗流力项作用于井筒周围形成的有效周向应力σ'θ2

其中ν为泊松比.

2.3 井筒周围有效周向应力场叠加

上一节已经推导得到了流体作用于井筒周围形成的有效周向应力场,除流体作用外,井筒周围水平有效构造地应力σeff-x和σeff-y作用形成的有效周向压应力[27]为

一般取r≥5a时,式(12)中地应力形成的周向应力就会衰减为原地应力状态,此时r就可视为是地应力施加的边界,即图2 中的外边界c.

根据Terzaghi 有效应力定律和弹性力学叠加理论[43],利用式(6)、式(7)、式(11)和式(12)即可推导得到井筒周围不同情况下的有效周向总应力

如式(13)所示: (1)未注入压裂液时井筒周围仅有地层有效构造应力的作用,所以有效周向总应力为Sθ1;(2)注入压裂液以后,若储层不可渗透不考虑渗流力的作用,则α=0 渗流力项消失,仅考虑井筒内外边界水压力作用形成的应力场,此时井筒周围有效周向总应力为Sθ2;(3)若压裂液渗流进入储层考虑渗流力的作用,则必须考虑渗流力项和面力项共同作用形成的应力场,此时井筒周围有效总周向应力为Sθ3.

利用式(13),对未注入流体时原地应力状态、注入流体施加井筒内压但储层不可渗透无渗流力的作用,以及储层可渗透考虑渗流力3 种条件下井筒周围的有效周向总应力进行了模拟分析,其井筒周围有效周向总应力分布云图如图3 所示,对应的最大水平主应力方向上的有效周向总应力随半径变化如图4 所示 (假设σeff-x=17.5 MPa,σeff-y=12.5 MPa,Po=2.5 MPa,Pw=15 MPa,ν=0.25,a=1 dm,c=10 dm,σt=0 MPa).

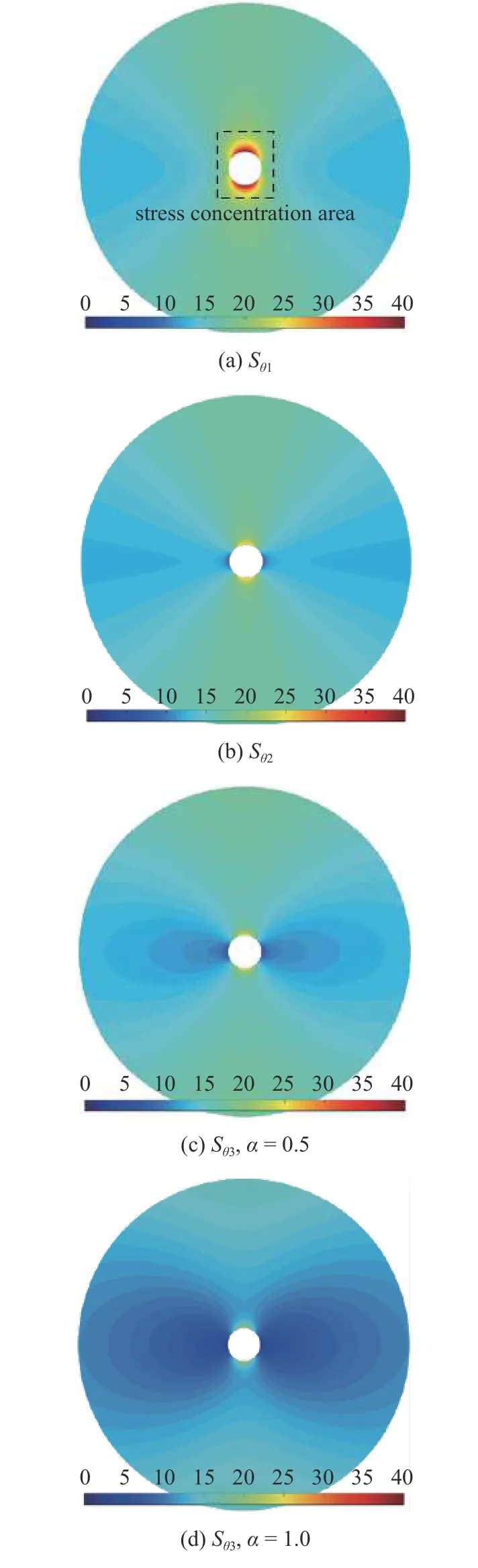
图3 不同条件下裸眼井筒周围有效周向总应力分布云图Fig.3 Effective circumferential total stress distribution around open hole wellbore under different conditions

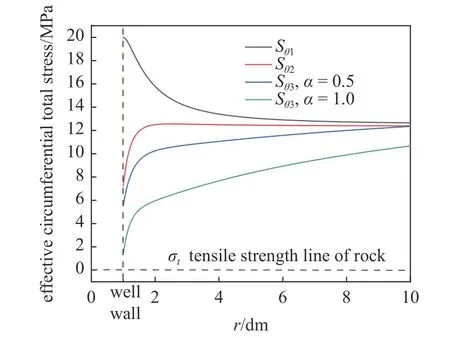
图4 不同条件下最大水平主应力方向(θ=0)井筒周围有效周向总应力随半径变化Fig.4 Distribution of effective circumferential total stress with radius around the wellbore in the direction of maximum horizontal principal stress (θ=0) under different conditions

从图3 可以看出,井筒未注入压裂液时,地应力形成的有效周向总应力为压应力,井壁周围出现明显的周向压应力远大于外边界的应力集中现象.当井筒注入流体施加井筒内压后,井壁周围的应力集中由于流体作用于井筒形成的拉应力作用被明显减弱.相比较不可渗透储层,流体渗流进入储层考虑渗流力作用时,井筒周围的有效周向压应力更小.相同压差下,Biot 有效应力系数越大,渗流力作用越强时井筒周围应力场被渗流力作用影响的范围越大,有效周向压应力也越小.

结合图4 进一步可以看出,施加井筒内压后,井壁处有效周向应力值最小,随着远离井壁,周向应力迅速恢复逼近原地应力状态.流体渗流进入储层,渗流力的作用显著减小了井壁处的有效周向压应力,使得井壁处有效周向应力值更加逼近岩石的抗拉强度线.Biot 有效应力系数等于0.5 时,相比较不可渗透储层无渗流力作用的红色曲线,渗流力作用(蓝色曲线)使得井壁处的有效周向压应力值降低了23%.由于水力裂缝通常沿着平行于最大水平主应力的方向起裂,因此结合图4 可以看出,流体渗流进入储层,渗流力作用显著增大了水力裂缝起裂的可能性,使得井筒壁面更容易发生拉伸破坏.

3 渗流力对裸眼井筒地层破裂压力的影响研究

预测地层破裂压力对于油田现场水力压裂工程设计至关重要,此前国内外已有许多学者利用最大周向拉应力准则[27,35,45]来分析预测裸眼井的地层破裂压力.经典的裸眼井地层破裂压力预测公式包括Hubbert 等[45]推导的经典的H-W 公式以及Haimson等[27]提出的H-F 公式

其中H-W 公式假设储层不可渗透不考虑压裂液滤失作用,而H-F 公式考虑了孔隙压力变化对多孔介质变形的影响,但该公式对固结方程进行了简化处理并忽略了边界效应[43],所以计算结果可能出现一定误差.因此在上一节分析得到的井筒周围有效周向应力场的基础上,本节基于最大周向拉应力准则推导了更加完备的渗流力作用下裸眼井地层破裂压力的解析解.

上一节模拟结果已经表明注入压裂液后,井壁处的有效周向应力最小,因此选择井壁处作为裂缝的起裂点.由最大周向拉应力准则可知,当井壁处最大水平主应力方向的有效周向总应力达到岩石的抗拉强度σt时,地层发生破裂,水力裂缝开始萌生

以垂直裸眼井形成垂直裂缝为例,令c≫a,r=a,θ=0 代入式(13)得到最大水平主应力方向井壁处的有效周向总应力Sθ3,然后令Sθ3=-σt,即可推导得到储层可渗透考虑渗流力作用时的地层破裂压力为

此前Muqtadir 等[34]利用室内压裂实验对致密砂岩岩心在不同压裂液黏度下裸眼井筒的地层破裂压力情况进行了研究,利用该项研究的实验结果,本文对经典的H-W 公式、H-F 公式以及式(16)的适用性进行了分析,对比结果如图5 所示.实验条件和具体的参数包括: 岩样直径5.08 cm,井筒直径0.635 cm (裸眼),最大最小水平主应力都为0.68 MPa,初始孔压为0 MPa,岩石抗拉强度12.3 MPa,Biot 系数为0.7,岩样平均渗透率1.3 mD,平均孔隙度为13.3%,压裂实验采用定流量加压方式.

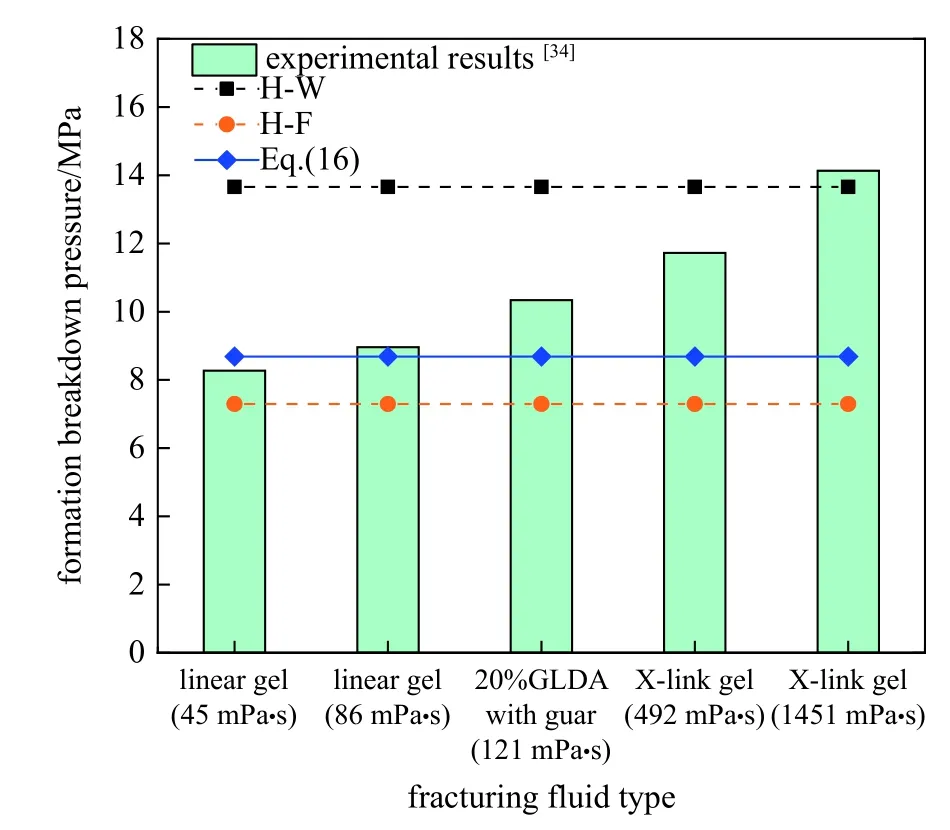
图5 不同压裂液类型下裸眼井地层破裂压力公式计算结果与实验结果的对比Fig.5 Comparison between experimental results and formula calculation results of formation breakdown pressure in open hole wells under different fracturing fluid types

从图5 可以看出,不同压裂液黏度条件下,裸眼井地层破裂压力差距很大,随着压裂液黏度的增大,地层破裂压力大幅增加.压裂液黏度越小,渗流作用越强时地层破裂压力越小.不考虑压裂液渗流作用的H-W 公式其预测结果明显高估了裸眼井的地层破裂压力,只有当压裂液黏度超高条件下(1451 mPa·s),H-W 公式才和实验结果较为接近.对于100 mPa·s以下的较低黏度压裂液(linear gel),压裂液渗流进入岩石孔隙考虑渗流力作用时,式(16)预测结果和实验结果更为接近,误差仅为5%左右;而H-F 公式的预测结果明显低估了裸眼井的地层破裂压力,误差高达10%以上.因此综合上述分析可以看出,当压裂液黏度很大流体难以渗流进入岩石孔隙时,H-W公式预测结果更为准确一些;而当压裂液黏度较小时,相比较H-F 公式,本文推导的裸眼井地层破裂压力式(16)可以更为准确地预测低黏度压裂液下裸眼井的地层破裂压力.

利用H-W 公式和式(16),本文对影响裸眼井地层破裂压力的不同因素进行了分析,结果如图6～图9 所示,其中黑色虚线代表储层不可渗透不考虑渗流力条件下H-W 公式计算的结果,而其余颜色实线是储层可渗透考虑渗流力时式(16)的计算结果(其中SH代表地层最大水平主应力,σeff-x=SH-Po;Sh代表地层最小水平主应力,σeff-y=Sh-Po,两向应力差为SH-Sh).

图6 不同两向应力差条件下垂直裸眼井地层破裂压力(假设ν=0.35,Sh=60 MPa,Po=30 MPa,σt=0 MPa)Fig.6 Formation breakdown pressure of vertical open hole under different stress differences

从图6 可以看出,储层不可渗透条件下地层破裂压力最大,当流体渗流进入储层时,渗流力作用下地层破裂压力开始减小.Biot 有效应力系数越大时,渗流力作用影响越占据主导因素,对应的地层破裂压力越小.随着最大水平主应力和最小水平主应力差值减小,不可渗透储层地层破裂压力和可渗透储层地层破裂压力差值越来越大,两向应力差更小的储层,渗流力作用对地层破裂压力的影响更明显.图7 为不同地层深度条件下的地层破裂压力,假设两向应力每100 m 均匀增大2.5 MPa,储层初始孔隙压力按照盐水的静液柱压力换算每100 m 均匀增大1.05 MPa.可以从图7 看出,随着地层深度增大,不同条件下的地层破裂压力也随着增大.地层深度越大,不可渗透储层地层破裂压力和可渗透储层地层破裂压力差值越大,深度更大的储层渗流力作用对地层破裂压力的影响更明显.

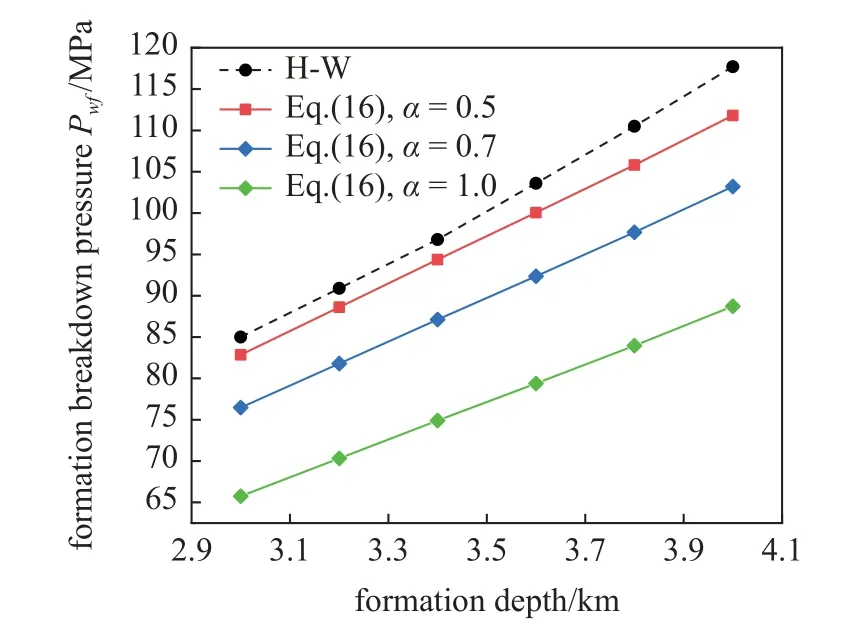
图7 不同地层深度条件下垂直裸眼井地层破裂压力(假设ν=0.35,地层深度3 km 处Sh=60 MPa,SH=65 MPa,Po=30 MPa,σt=0 MPa)Fig.7 Formation breakdown pressure of vertical open hole wells under different formation depths

从图8 可以看出,储层岩石泊松比越小,地层破裂压力越大.泊松比更大,脆性更强的储层,渗流力作用对裸眼井地层破裂压力的影响更显著.图9 表明随着岩石抗拉强度的增大,不同条件下地层破裂压力也随之增大.岩石抗拉强度更大的储层,渗流力作用对地层破裂压力的影响更显著.综上所述可以看出,压裂液渗流进入储层,渗流力的作用显著减小了裸眼井的地层破裂压力.Biot 有效应力系数、两向应力差、储层深度以及泊松比都对渗流力作用下裸眼井的地层破裂压力有显著影响.Biot 有效应力系数和泊松比越大、抗拉强度越小,地层破裂压力越小.两向应力差较小,而泊松比、地层深度、抗拉强度较大的储层,渗流力作用对地层破裂压力的影响更显著一些.

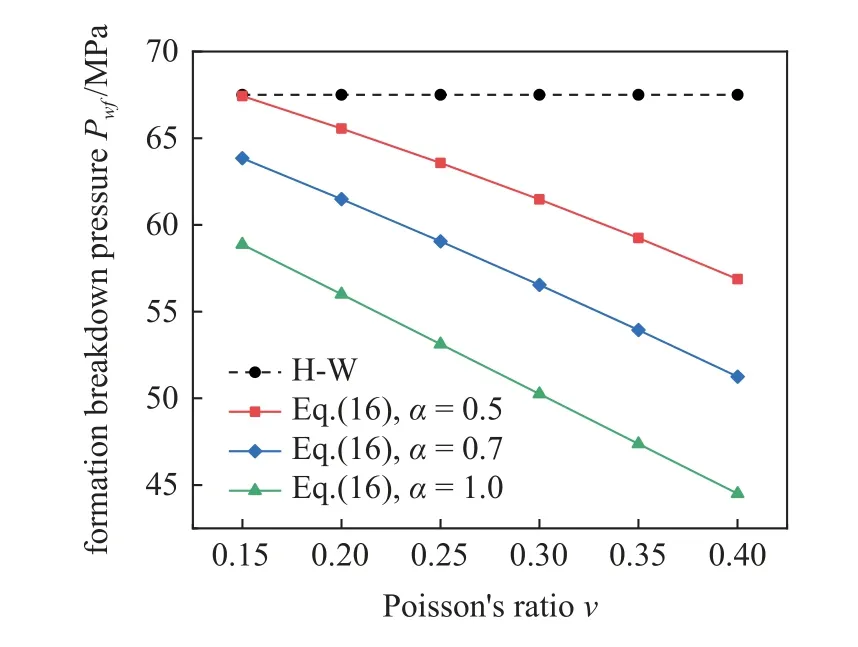
图8 不同泊松比条件下垂直裸眼井地层破裂压力(假设Sh=40 MPa,SH=42.5 MPa,Po=30 MPa,σt=0 MPa)Fig.8 Formation breakdown pressure of vertical open hole wells under different Poisson's ratios

图9 不同抗拉强度条件下垂直裸眼井地层破裂压力(假设Sh=40 MPa,SH=42.5 MPa,Po=30 MPa,ν= 0.35)Fig.9 Formation breakdown pressure of vertical open hole wells under different rock tensile strengths

4 结论

本文基于Biot 孔隙固结理论分析了流体渗流进入岩石孔隙时,渗流力对储层岩石的作用机理.以裸眼井筒为例,研究了渗流力对井筒周围有效周向应力场的影响机理,推导了考虑渗流力作用的裸眼井筒地层破裂压力解析解公式,揭示了渗流力作用下不同因素对裸眼井地层破裂压力的影响规律,文章主要结论如下.

(1)孔隙压差很小等于一个大气压时,单位立方厘米岩样所受体积力渗流力的大小远超同等大小岩样所受体积力重力的大小,渗流力对储层岩石的作用完全不可忽视.

(2)工作液渗流进入储层岩石孔隙时,岩石骨架受力由流体施加给岩石骨架的渗流力-体积力项和作用于岩石表面的法向水压力-面力项两部分组成.Biot 有效应力系数控制着流体施加给岩石单元体渗流力和面力的大小,Biot 有效应力系数越大,渗流力对岩石骨架变形的影响程度越大.

(3)压裂液渗流进入储层可以显著降低裸眼井筒周围的有效周向应力值,渗流力作用明显增大了井壁发生拉伸破裂的可能性.相同压差下,Biot 有效应力系数越大,渗流力作用越强时井筒周围应力场被渗流力作用影响的范围越大.

(4)渗流力作用可以显著降低裸眼井的地层破裂压力.地层深度越大,两向应力差越小时渗流力作用对地层破裂压力的影响越显著;岩石Biot 有效应力系数和泊松比越大,抗拉强度越小时,渗流力作用下裸眼井地层破裂压力越小.

本文建立的渗流力理论力学模型可为后续分析瞬态渗流力作用对水力裂缝起裂与扩展的影响奠定理论基础,推导的裸眼井筒地层破裂压力预测公式可为水力压裂施工方案的优化设计提供理论支撑.

附录A

在上下围岩的限制下,井筒周围应力场通常按照平面应变条件进行求解,本文同样选择平面应变条件来求解圆筒周围渗流力作用形成的应力场,具体的推导过程如下.

首先对于平面应变条件,极坐标系下弹性力学物理方程满足

其中E代表杨氏模量,GPa;ν代表泊松比.

将弹性力学几何方程ɛr=du/dr,ɛθ=u/r代入式(A1)得到

对孔隙分布方程(10)求偏导,得到渗流力项为

将方程(A2)和方程(A3)共同代入渗流力作用下的平衡微分方程(9)得到

进一步得到

对上式进行积分变换得到位移方程

将位移方程(A6)代入几何方程ɛr=du/dr,ɛθ=u/r中,再将ɛr与ɛθ代入平面应变条件下的物理方程(A1)中即可得到径向应力与周向应力

单独求解圆筒周围渗流力作用形成的有效应力场时,其应力场边界条件为

将渗流力单独作用下圆筒周围的应力边界条件(A8)代入方程(A7)可联立求解得到

将系数A和B代入方程(A7)最终得到圆筒周围渗流力单独作用形成的有效应力场分布