机器人在轨组装结构的耦合动力学与步态优化1)

杨胜丽 吴志刚 孟得山,2) 李庆军 邵 可

* (中山大学航空航天学院,广东深圳 518107)

† (西北工业大学民航学院,西安 710072)

引言

空间望远镜、通信天线、太阳帆等大型航天器是未来空间任务的主要发展方向之一[1-4].但由于其尺度大,运载火箭无法一次带入太空,因此可将其分解为多个组装模块,由运载火箭载入太空在轨组装,航天员在轨组装大型航天器难度大且十分危险,采用机器人在轨组装是大型航天结构最有发展潜力的方式之一[5-7].

各国正在积极研发用于自主组装的空间机器人系统[8],目前常见的在轨组装机器人分为自装配机器人和附着型装配机器人[9],典型的自装配机器人有轨道快车、机器人装配与服务基础设施(CIRAS)、地球同步轨道卫星机器人服务(RSGS)[10-12],这类机器人的操作范围受工作空间限制,不适用于大型航天结构的组装.而附着型装配机器人可在航天器表面自主移动,工作范围能够覆盖整个航天器.比较典型的附着型装配机器人有双足各向同性晶格定位探索者机器人BILL-E、仿人型机器人Robonaut 2、空间结构附属移动机器人Skyworker 和三分支机器人[13-17].其中三分支机器人具备操作灵活、适应性强等特点,采用其依附在结构表面行走组装是大型航天器在轨建造的有效途径.然而,航天器结构的大型化和柔性化使得其抗变形能力很弱,一旦受到外部激励很容易激发结构振动并且很难自行衰减下来[18-19].当机器人依附在结构表面行走组装时,机器人行走不当可能激发结构大幅振动.因此机器人在轨组装过程中的动力学与结构振动控制问题对于大型航天器的构建至关重要[20].

国内外学者开展了针对机器人在轨装配过程中的动力学与控制问题的研究.武廷课等[21]考虑多臂机器人与薄膜天线的耦合作用,分别利用单向递推组集方法和有限元方法建立多臂机器人的动力学模型和空间薄膜天线系统的动力学模型,通过调整机器人末端柔性阻尼执行器对薄膜天线的振动进行抑制.刘菲[22]通过约束力算法建立多臂机器人在大型航天器表面移动的动力学模型,采用依赖系统模型和参数的反馈线性化与PD 控制方法,针对多臂机器人移动过程设计能跟踪期望轨迹的控制器.王启生等[23-24]采用自然坐标法和绝对节点坐标法建立了双臂空间机器人在轨组装超大型结构过程中的动力学模型,分析了系统参数对组装过程动力学响应的影响,并通过轨迹规划和轨迹跟踪控制实现机器人空间组装超大型结构的动力学仿真.陈钢等[25]针对多臂机器人抓取稳定性的接触力不平衡与接触振动问题,提出了力分配与柔顺控制策略.荣吉利等[26]将大型空间结构视为刚柔多体系统,分别采用自然坐标法和绝对节点坐标法对刚性构建和柔性桁架结构进行建模,并采用摆线运动插值函数作为控制方程提高展开过程的稳定性.Tang 等[27]使用达朗贝尔原理结合欧拉-伯努利梁理论建立大型柔性细长桁架结构携带机械臂的动力学模型.卢国新[28]建立了空间柔性基座机器人的刚柔耦合动力学模型,并通过分析柔性基座振动与机器人运动的关系,提出了一种有效提高机器人运动控制精度并抑制基座振动的控制方法.李辉[29]采用基于铰接体概念的空间向量法对空间站多臂机器人进行动力学建模.Reyhanoglu等[30]使用拉格朗日方法建立了柔性结构上安装刚性机械臂的非线性动力学模型,并采用基于Lyapunov的反馈控制法来抑制柔性结构的振动.Yao 等[31]针对机械臂操作大型柔性模块的振动问题,提出了一种用于柔性模块轨迹跟踪中振动最小化的两重时间尺度控制方案.

上述研究工作主要面向的是组装过程中机器人基座固定不动与空间结构的耦合动力学及控制问题.目前针对行走移动机器人与空间结构的耦合动力学与振动抑制问题的研究较少.周威亚等[32]将机器人在空间结构上的移动情况等效为脉冲载荷按交替步加载到空间结构上,并结合卡尔曼滤波算法设计了一种能够有效抑制组装过程中空间桁架结构振动的线型二次型最优振动控制器.Cao 等[33]将在轨装配机器人的运动类比于经典的车桥耦合动力学模型进行描述.Swei 等[34]建立了一种行走在大型柔性结构上的机器人-结构耦合动力学模型,并提出了一种结合标准全状态反馈运动控制器和自适应控制器以实现机器人的轨迹跟踪.但是,上述工作均只研究了机器人相对于结构接触位置变化时的动力学与控制问题,并未考虑机器人行走运动过程中包含机器人关节运动和行走移动两个不同的运动过程.

目前对于机器人行走步态对空间柔性结构的动力学响应影响缺乏深入分析讨论.本文以如图1 所示的三分支空间机器人在轨组装空间太阳能电站为研究对象,研究考虑机器人关节运动和行走移动的机器人与结构耦合动力学问题.基于拉格朗日方程和欧拉-伯努利梁模型建立机器人与结构的耦合动力学模型,推导结构振动与机器人运动的关系,分析结构在机器人在不同运动下的动力学响应,并进一步研究通过步态优化调整机器人运动以抑制空间结构振动.以期为机器人行走组装大型空间结构的动力学建模与结构的振动抑制工作提供参考.

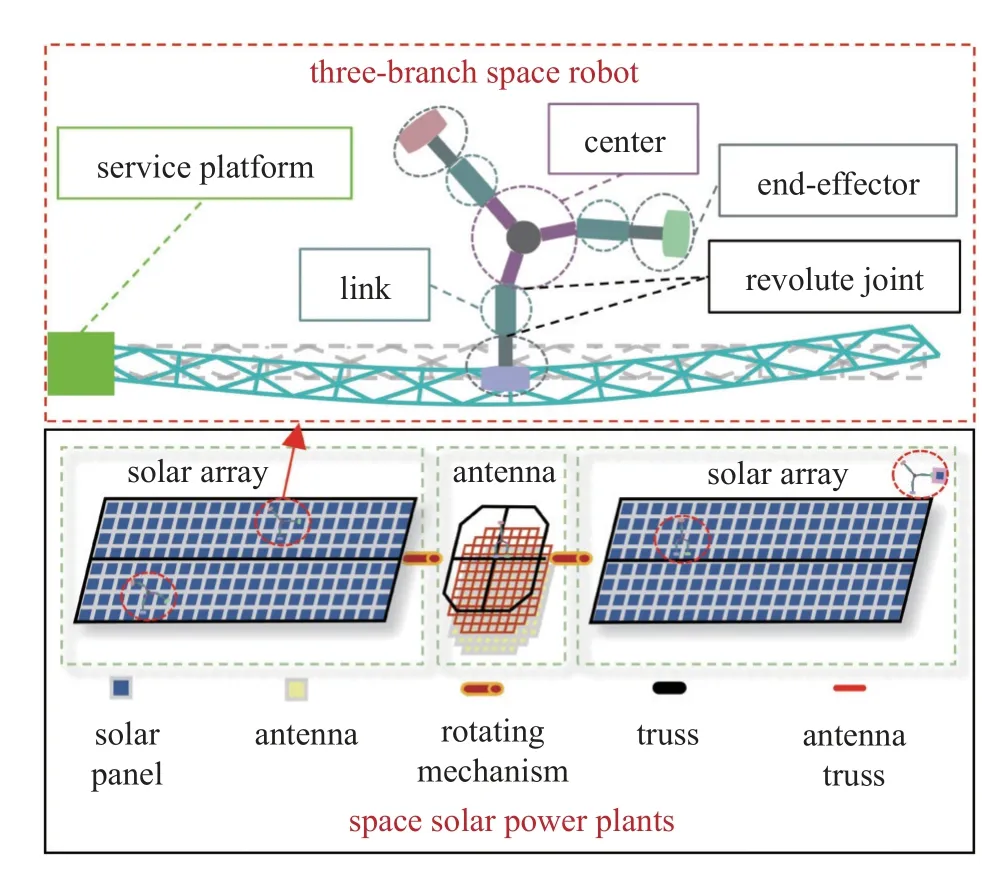
图1 三分支机器人在轨组装空间太阳能电站示意图Fig.1 Schematic diagram of three-branch robot on-orbit assembly of space solar power plant

1 机器人-结构耦合动力学建模

1.1 研究对象

三分支机器人如图2 所示,机器人由3 个分支和末端操作工具组成,每个分支包含一个3 自由度机械臂和一个末端工具.任意两分支可组成一个6 自由度机械臂,每两个分支之间机械臂的构型完全一样.本文选择由分支1 和分支2 构成的6 自由度机械臂来进行分析.根据修正D-H 法确定机器人的D-H 参数如表1 所示,其详细运动学推导见文献[17].

表1 D-H 参数表Table 1 D-H parameter

机器人行走在结构上的耦合系统如图3 所示.机器人通过末端工具与结构在接触点处连接,接触点不变时,机器人与结构之间的相互作用力随着机器人关节的运动而改变,随着机器人在结构上移动,机器人与结构之间的相互作用力随着接触点位置的改变而改变.通过分时复用3 个分支可以实现机器人依附在结构上灵活移动并执行模块运输与装配任务.本文以空间结构-单个组装机器人系统为研究对象,建立机器人-结构耦合动力学方程,研究行走移动组装机器人与其组装结构的耦合动力学.

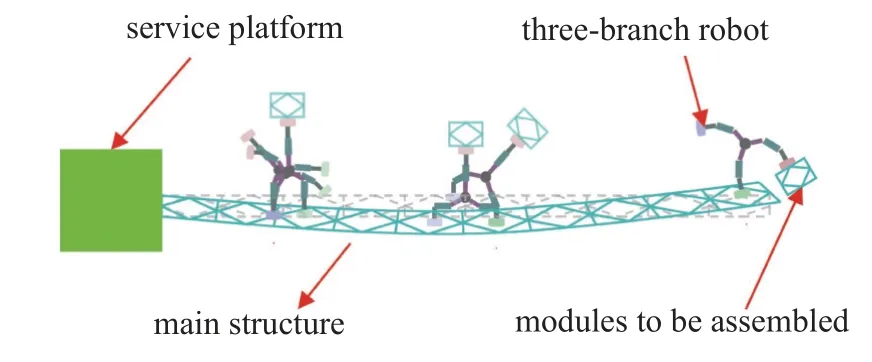
图3 机器人-结构耦合系统Fig.3 Robot-structure coupling system

1.2 三分支机器人动力学

相较于大型空间结构而言,三分支机器人尺寸小、刚度大,因此将机器人简化为多刚体系统,并对机器人作以下几点假设: (1)假设机器人的3 个分支末端的空间旋转关节处于锁定状态;(2)忽略关节柔性、摩擦和微重力等因素的影响.于是耦合系统中的机器人可简化为如图4 所示的简化模型.其中,mi,Ii,li,i=1,2,···,7;表示各部件的质量、惯性矩及连杆长度.θi和τi表示三分支机器人各关节角度和施加于各关节的力矩,i=1,2,···,6;z(x,t)表示空间结构与机器人分支末端接触位置处在竖直方向的变形量,fz表示机器人与结构间的相互作用力.

使用拉格朗日方程建立其动力学模型

其中,L为拉格朗日算子,T为系统的总动能,V为系统的总势能,Q为广义力,q为广义坐标.系统总动能为机器人各连杆动能的总和,同理,系统总势能为机器人各个连杆势能的总和.通过推导得到耦合系统中机器人的动力学方程为

其中,Hb为分支末端等效的机器人质量,Hbm为机器人与结构之间的耦合惯性矩阵,Hm为三分支机器人的惯性矩阵,z为结构在竖直方向的变形,θ为机器人的各关节向量,Cb为结构的非线性速度相关项,Cm为机器人的非线性速度相关项,fz为结构与机器人之间的相互作用力,τ为三分支机器人的关节力矩.式(2)的动力学方程是高度耦合非线性的,并且机器人与结构之间的相互作用力fz未知,因此需要进一步结合结构动力学方程来分析.

1.3 空间结构动力学

机器人运动会对空间结构产生激励,由于机器人与结构在接触点固连,因此激励与机器人和结构间的相互作用力大小相等,方向相反.将空间结构等效为欧拉-伯努利悬臂梁,则空间结构在xr处受到机器人对结构施加的激励作用时的横向振动方程为

式中,ρ为梁的密度,Ι为截面对中性轴的惯性矩,A为梁的横截面积,E为弹性模量,-fzδ(x-xr) 表示结构在xr处所受的力,δ为狄拉克函数.假设EI和ρA都为常值,使用Ritz-Galerkin 方法,梁的横向变形可近似为

式中,Φi(x)表示第i阶模态的振型函数,vi(t)表示广义坐标(或变形量),n表示保留的模态阶数.对于长度为l悬臂梁,其振型函数为

其中,μil为特征方程cos(μl)·cos(μl)=-1 的解.因此将式(4)代入梁的横向振动方程式(3)得到

式(6) 左右同时乘以Φj(x),并沿梁长l对x积分,有

写成矩阵形式有

式中

其中,Ms ,Ks表示结构的等效质量矩阵和等效刚度矩阵.

1.4 机器人-结构耦合动力学建模

由式(4)给出空间结构在xr处的横向变形写成矩阵形式为

将式(11)代入组装过程中的机器人动力学方程式(2),并与结构动力学方程联立可化简得到机器人与结构的耦合动力学方程

通过式(12)的下半部分可推导出机器人关节运动与结构模态坐标之间的关系

化简得到

其中,Mc为耦合质量矩阵;Fc为机器人运动产生的模态载荷激励.式(14)为机器人运动与结构振动(模态坐标)之间的关系,对其进行求解可求出耦合系统中机器人运动对结构振动的影响.

2 机器人行走步态轨迹优化

2.1 蠕动步态规划过程

机器人的蠕动运动步态的运动过程和规划流程如图5 所示.其中ts表示步态周期,ls表示运动步长,hs表示抬起高度;红色、黄色和蓝色圆点分别表示a,b和c点.

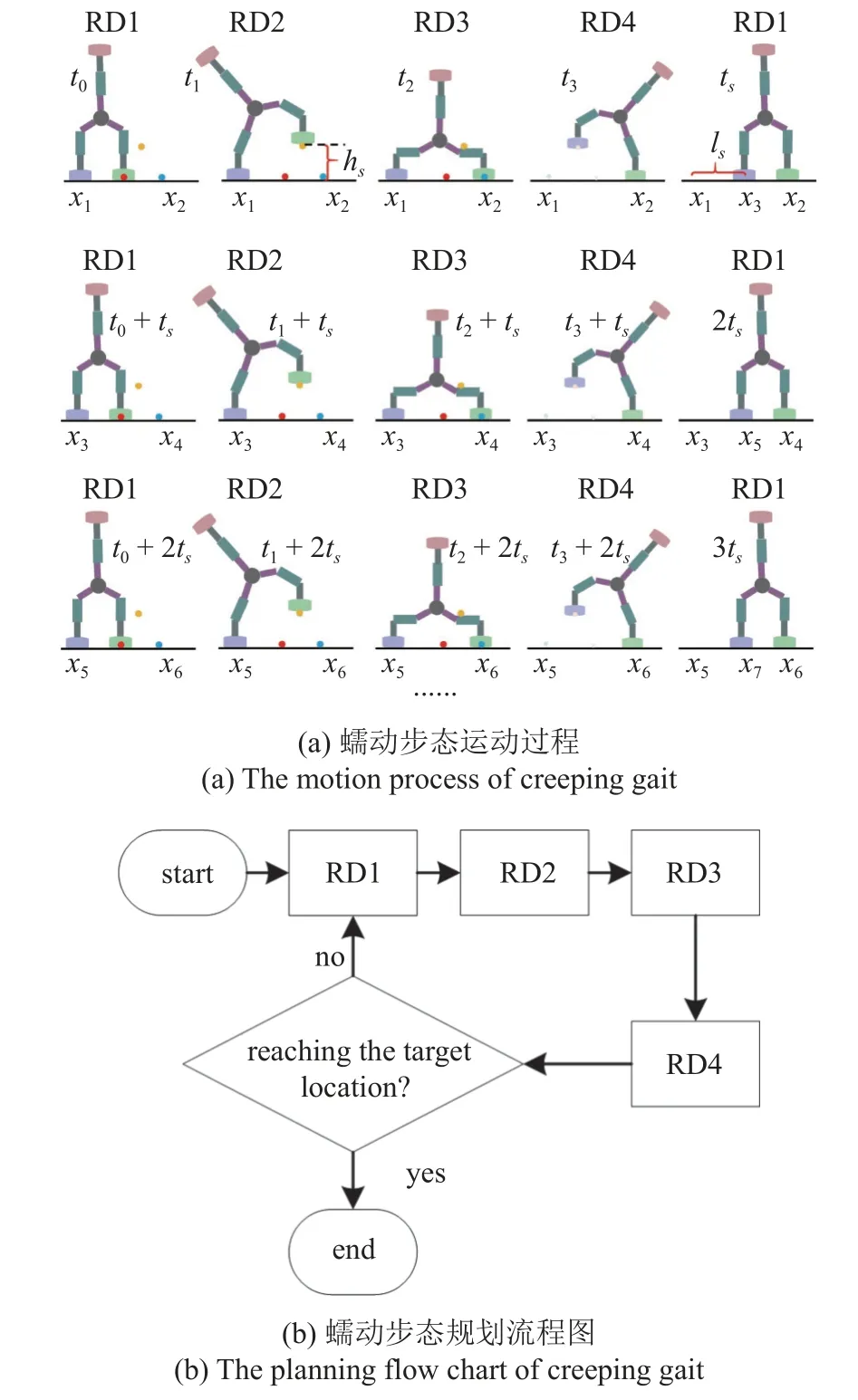
图5 机器人蠕动步态运动规划Fig.5 Robot creeping gait motion planning

具体的蠕动步态规划过程如下.

(1) 机器人处于初始位置,左侧分支记为分支1,右侧分支记为分支2,两分支均固定在结构上,分支2 末端位于开始位置a点,分支1 与分支2 的姿态对称,各关节角的绝对值相等.此时机器人处于状态1,记为RD1.

(2) 分支1 末端保持与结构固连,分支2 末端操作工具释放,关节1,2,3 和4 协调运动,直至分支2 末端运动至中间位置b点,机器人由RD1 转换为状态2,记为RD2.

(3) 分支1 末端继续保持固定,直至分支2 末端运动到目标结构位置c点,同时将分支2 末端与结构固连,此时机器人由RD2 转换为状态3,记为RD3.

(4) 分支2 末端保持固定,同时释放分支1 末端,关节1,2,3 和4 协调运动使机器人运动至与RD2 对称,此时机器人各关节角度与RD2 对称,机器人处于状态4,记为RD4.

(5) 分支2 末端继续保持固定,分支1 末端运动至结构目标位置,然后将分支1 末端与结构固定,此时机器人除了相对于结构的位置与RD1 不同外,机器人的各关节角和姿态与RD1 完全相同.至此,机器人完成了一个蠕动步态周期的运动,一个步态周期时间记为ts;分支1 末端移动的距离为机器人行走的步长,记作ls;分支末端经过中间点时的抬起高度记为hs.

由蠕动步态的运动规划可知,一个步态周期分为前半个周期分支2 末端迈出与后半个周期分支1 末端收回两个过程.在前半个周期中,机器人从RD1 运动至RD2 再运动至RD3,即分支2 末端在伸展过程中分别在t0时刻、t1时刻和t2时刻经过初始位置a点、中间位置b点和目标位置c点,对3 个位置进行逆运动学[17]求解可得到机器人前半个周期运动过程中各状态对应的各关节角度.后半个周期运动过程中机器人的姿态与前半个周期对称.因此机器人一个蠕动步态周期内各状态对应的各关节角度如表2 所示.

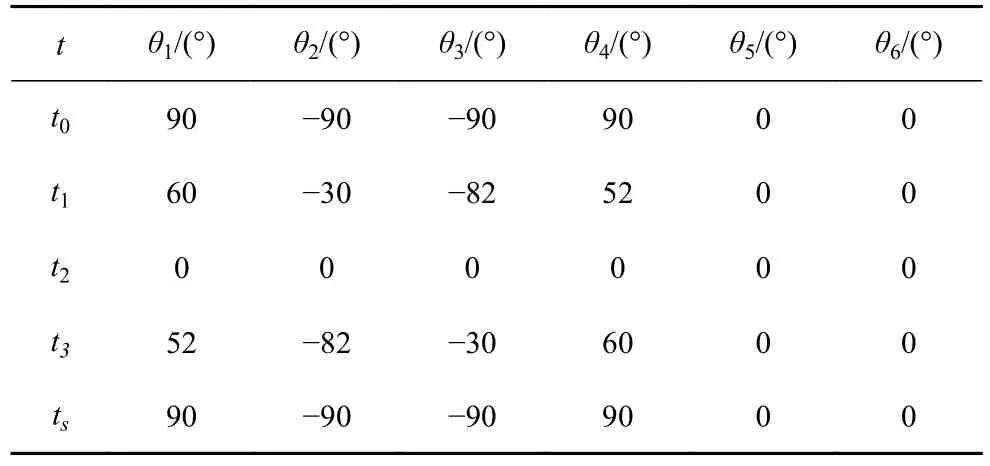
表2 蠕动步态各时刻各关节角度Table 2 Angle of each joint at each moment of creeping gait

使用通过中间路径点的轨迹规划方式对机器人各关节轨迹进行轨迹规划.假设分支2 末端经过a点和c点的速度为零.由于机器人做的是周期性运动,因此机器人各关节的轨迹也是周期性的.

2.2 基于5 次多项式与有限项余弦傅里叶级数之和的关节轨迹参数化

由机器人-结构耦合动力学方程可知,结构的横向振动能够通过机器人的关节运动轨迹求解,结构振动会影响机器人的末端轨迹跟踪,因此需要对机器人-结构耦合系统中空间结构的振动进行抑制.本节对机器人蠕动步态进行轨迹优化调整,使得机器人运动对结构产生的扰动减小,从而能够稳定高效地完成空间结构的在轨组装任务.本节采用含参数的轨迹规划函数结合粒子群优化算法对机器人的运动步态进行优化,即对关节空间的角度、角速度、角加速度进行轨迹规划,主要步骤如下.

Step1: 根据机器人-结构耦合动力学方程,推导机器人运动与结构振动之间的关系;

Step2: 构造含参数的关节轨迹函数,以其中的待定参数作为待优化变量,轨迹规划问题转化为待定参数寻优问题;

Step3: 根据结构振动与关节运动的关系,构造使结构产生最小残余振动的目标函数;

Step4: 利用粒子群优化算法寻找使得目标函数最小的关节轨迹参数,将该参数代入关节轨迹函数即可求得能够抑制结构振动的关节轨迹.

5 次多项式插值常被用于通过中间路径点运动的关节角度规划,多项式函数完全能够满足通过中间路径点运动的边界条件,但包含激发系统共振的不必要的高次谐波,并且多项式函数无法通过增加多项式的项来保证求解的收敛性,只用5 次多项式对通过中间路径点的运动进行轨迹规划也不能达到很好的抑制结构振动效果;然而傅里叶级数展开式能够通过增加项数来保证收敛,但无法满足边界条件.因此结合两个函数的优势考虑采用5 次多项式与有限项余弦傅里叶之和的方式对关节角度进行轨迹规划.

下式为各关节角度轨迹表达式

对于这个多项式而言,根据蠕动步态的初始终止各个关节的角度信息,可使用式(16)的边界条件进行约束

将5 次多项式的5 次项系数a15,a25和傅里叶级数系数λ1m和λ2m作为需要设计的变量,则5 次多项式的剩余前4 项系数a10,a11,a12,a13,a14,a20,a21,a22,a23,a24可根据设计系数和式(16)的边界条件求得.因此,当傅里叶级数系数λim(i=1,2;m=1,2,···,M)和5 次项系数ai5(i=1,2)确定了,关节轨迹的角度、角速度和角加速度也就确定了.于是,机器人轨迹规划问题即转化为确定待定参数ai5和λim的问题.

2.3 基于粒子群优化算法的轨迹参数优化

结构的横向振动能够通过机器人的运动轨迹求解,机器人各个关节采用前面介绍的轨迹规划方式,因此结构的振动可通过待定参数来描述.假定待定参数用λ来描述,则结构的振动位移可表示为

为了避免机器人运动过程中产生过大的加速度对机器人的稳定性造成影响,构造出的关节轨迹除了需要满足使结构振动最小的目标外,还需要限制机器人运动过程中各关节的角加速度.因此,构造如下目标函数

式中,zmax(λ)为在待定参数下结构的最大振动位移,(λ)为各关节角加速度的最大值,kz和ka为加权系数,使不同量纲的物理量经过加权后能进行叠加,一般由误差容许范围来设定加权系数.kz表示结构残余振动位移的最大允许值,ka表示机器人运动过程中各关节角加速度的最大允许值.优化的目的是使目标函数最小.

3 仿真分析

为研究空间机器人在大型空间结构上行走移动时对空间结构耦合动力学响应的影响,以机器人蠕动运动步态为例,研究空间结构在蠕动步态行走下的耦合动力学响应,并通过轨迹参数化结合粒子群优化算法找到能够减小空间结构振动的运动轨迹参数.假设悬臂梁的长度为10 m,密度为122 kg/m3,横截面积为1 m2,截面惯性矩为2.08×10-2m4,弹性模量为24.5 MPa.三分支组装机器人的质量和几何参数见表3.

表3 三分支组装机器人的参数Table 3 Parameters of the three-branch assembly robot

3.1 机器人行走时的耦合动力学响应分析

空间结构在机器人蠕动步态行走运动下的横向振动可由机器人-结构耦合的动力学方程式(14)求解.为了研究机器人以蠕动步态在结构上运动对结构振动的影响,本节采用5 次多项式插值轨迹规划方式在关节空间对机器人运动步态进行轨迹规划,仿真得到空间结构在机器人以不同行走步频、步长及不同的抬起高度下的动力学响应.

图6 为机器人从结构中间位置向自由端行走5 步之后停止运动过程中结构的动力学响应,机器人运动的步态周期为4 s,前20 s 为机器人行走过程中的结构振动,后10 s 为结构的残余振动.其中图6(a)为结构的整体变形,图6(b)为结构末端的振动位移.其中实线表示机器人行走过程的结构振动,虚线表示机器人停止运动后结构的残余振动.从图中可以看出,机器人的运动激发了结构振动,随着机器人向自由端行走的过程中,由于振动的叠加使得结构振动的振幅逐渐增大,并且当机器人运动停止时,结构会持续振动.

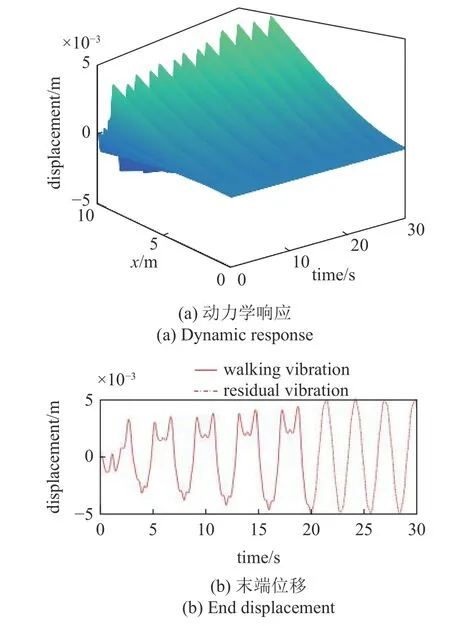
图6 动力学响应与末端位移Fig.6 The dynamic response and the end displacement

图7(a)～图7(c)分别为机器人不同步频、不同行走步长以及不同抬起高度下结构末端的振动位移,从仿真结果可以看出,机器人运动步频越快,结构振幅越大.由于机器人运动一步过程中涉及两个不同分支末端分别在结构的不同位置处对结构产生载荷激励,所以机器人运动步频接近结构基频(0.36 Hz)的两倍时结构振幅最大.此外,机器人运动的步长越长、抬起的高度越高,结构的振幅越大.

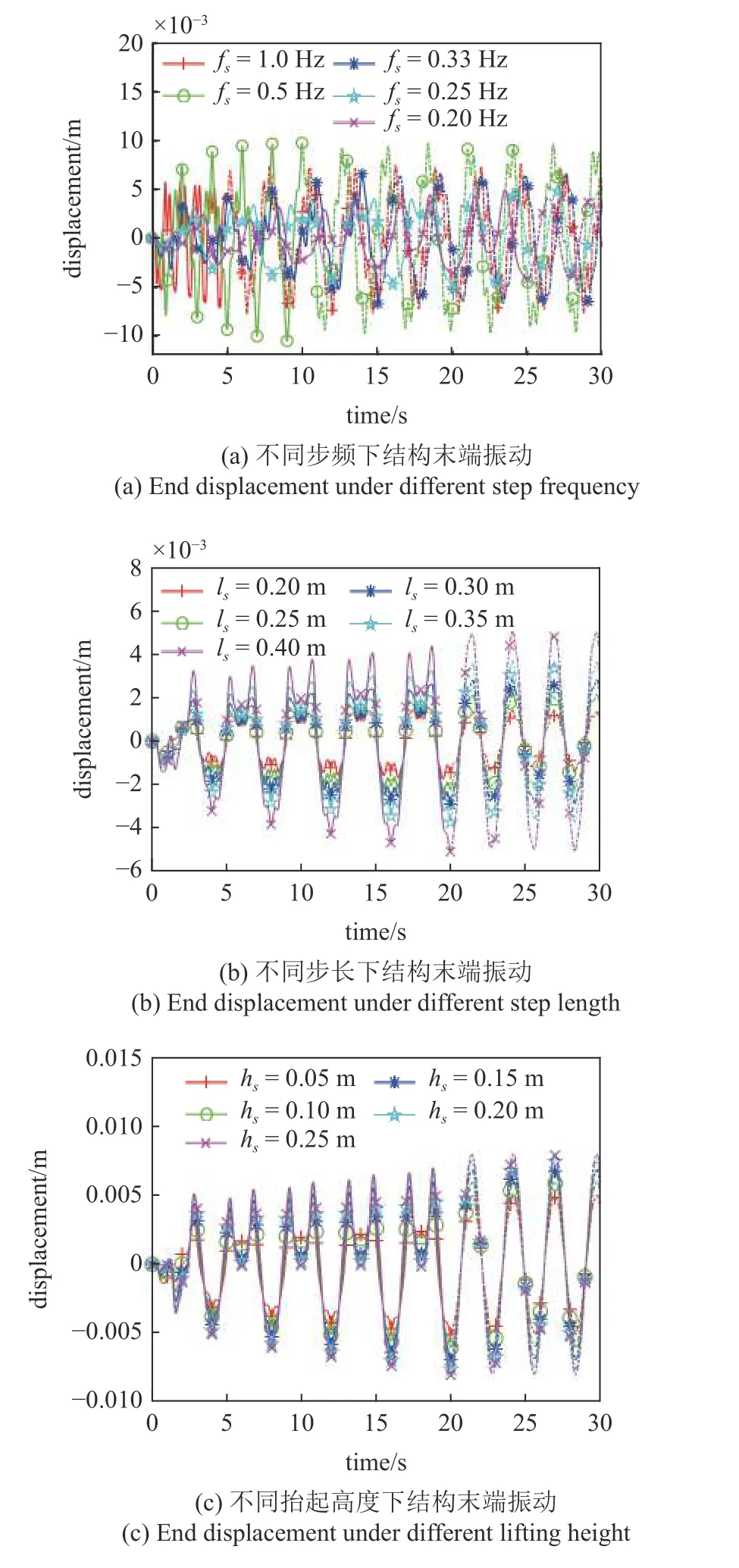
图7 结构末端振动位移Fig.7 Vibration displacement at the end of the structure

3.2 轨迹优化仿真结果

为了研究机器人如何行走产生的结构振动最小.本节首先分析了两种不同轨迹规划方式对结构动力学响应影响,然后采用第2.3 节的优化方法优化得到使结构振动最小的机器人轨迹.其中轨迹规划方式分别采用5 次多项式插值规划式

和5-3 组合多项式插值规划式

轨迹优化方法中的傅里叶级数项数M=3,结构振动位移的最大允许值kz=0.005 m,机器人运动过程中各关节角加速度的最大允许值ka=π rad/s2.在寻找优化参数的PSO 算法中,种群粒子数和最大迭代次数分别为48 和2000,待优化参数范围为ai5∈[-2,2],i=1,2,λim∈[-10,10],m=1,2,3.本节的一个蠕动步态周期取6 s,机器人从中间位置向自由端行走5 步,总的仿真时间为50 s,后20 s 用于研究残余振动的情况.

图8 和图9 为采用不同轨迹规划方式运动一个步态周期的各关节角度和加速度曲线.关节角度曲线表明3 种不同轨迹规划方式下机器人各关节都能都运动至目标位置.角加速度曲线表明采用轨迹优化方法规划出的关节角加速度比5-3 组合多项式和5 次多项式轨迹规划的小.同时,轨迹优化方法还调动了轨迹规划方法中未使用到的第3 个分支上关节5 和关节6.

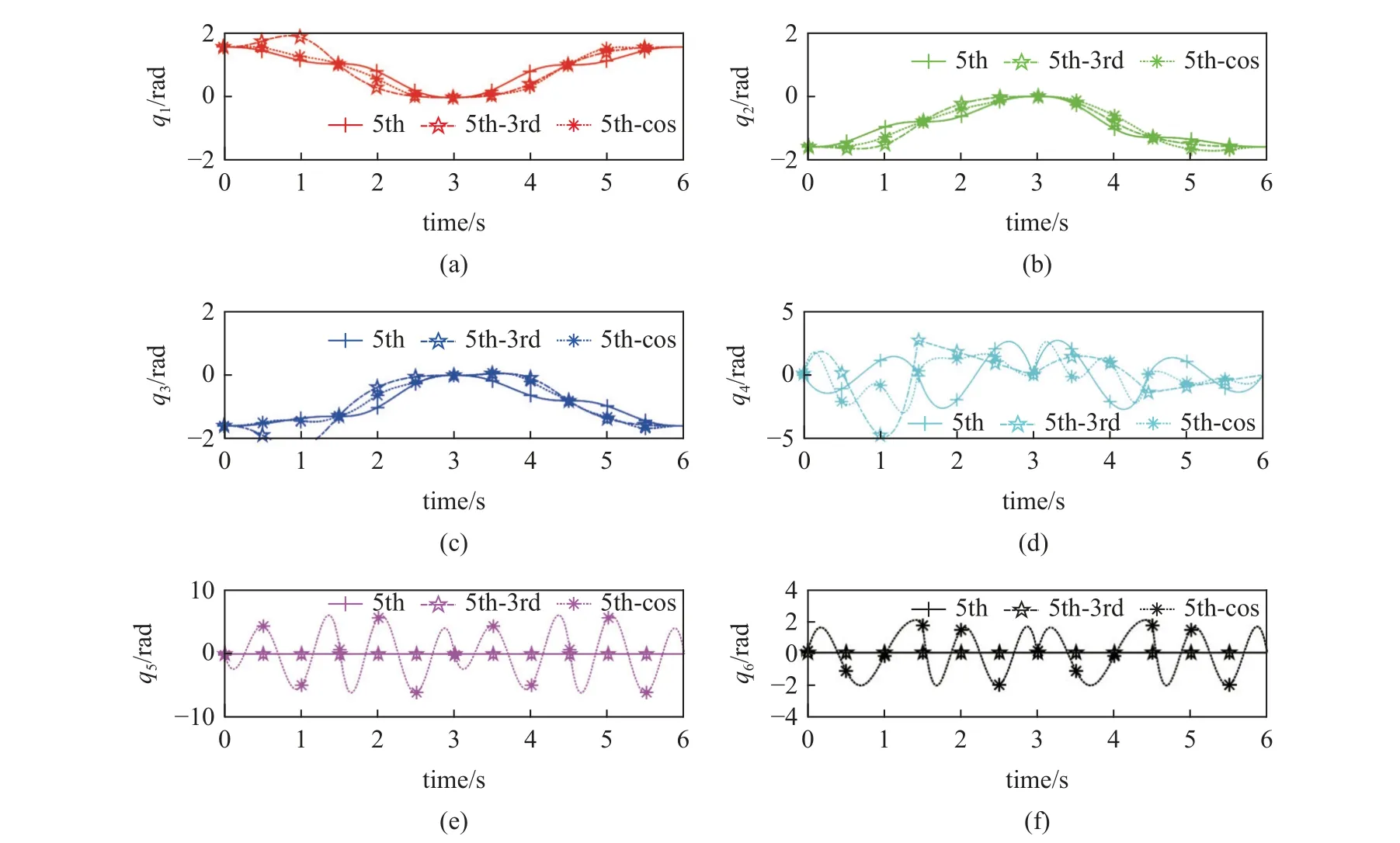
图8 不同轨迹规划方式下机器人各关节角度Fig.8 Angle of each joint of the robot under different trajectory planning methods

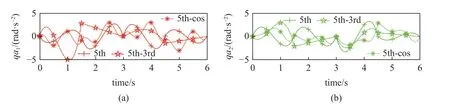
图9 不同轨迹规划方式下机器人各关节角加速度Fig.9 Angular acceleration of each joint of the robot under different trajectory planning methods

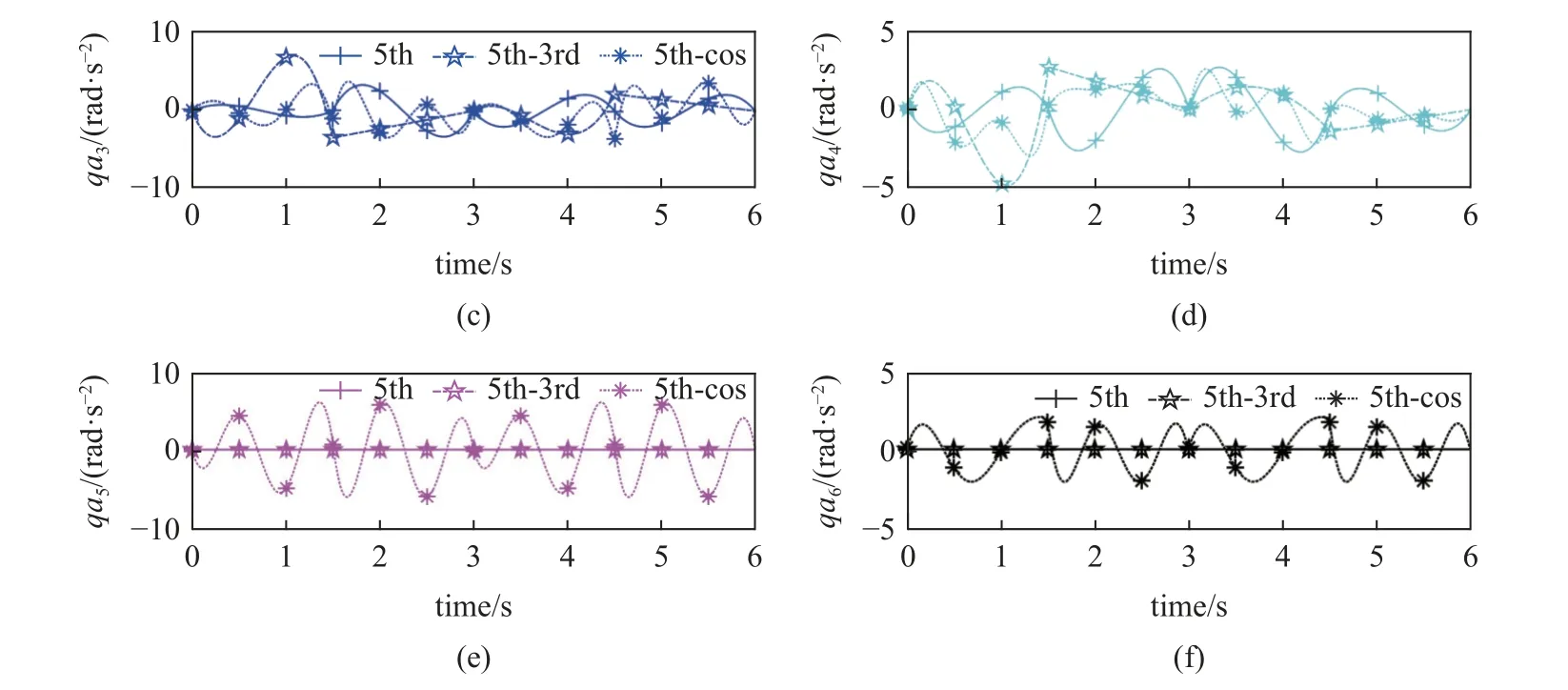
图9 不同轨迹规划方式下机器人各关节角加速度 (续)Fig.9 Angular acceleration of each joint of the robot under different trajectory planning methods (continued)

图10 为机器人不同行走方式下结构末端点的振动位移.从图中可以看出,采用轨迹优化方法规划的机器人运动方式激发的结构振动比未优化的两种轨迹规划方式小.由此可得出结构的振动与机器人的运动方式息息相关,当轨迹规划出的机器人运动加速度越小,结构振动越小.此外,冗余的第3 分支对结构的振动抑制也起了一定作用.因此,可通过机器人步态轨迹优化的方式来抑制机器人行走运动过程中结构的振动.

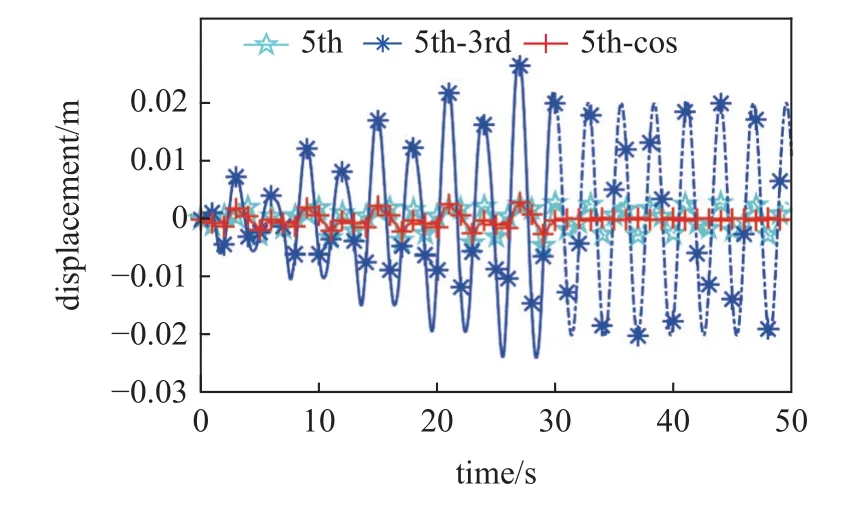
图10 结构的末端点位移Fig.10 The end point displacement of the structure

4 结论

面向机器人行走组装大型空间结构的任务需求,本文建立了一种移动机器人与结构的耦合动力学分析模型,对机器人在不同蠕动步态下的结构动力学响应进行了仿真分析,并且提出了采用机器人步态优化的方式来抑制结构振动.仿真结果表明,结构振动与机器人的运动步频、步长且抬起高度以及轨迹规划方式息息相关.当机器人行走的步频越快、步长越长且抬起高度越高,其激发的结构振动越大.并且当步频接近结构的固有频率的两倍时会激发共振,导致结构产生较大振动.此外,基于5 次多项式与有限项余弦傅里叶级数之和的轨迹优化方法比常规的5-3 组合多项式和5 次多项式规划步态所激发的结构振动要小,并且能够有效利用行走移动中冗余的第3 分支.因此,对于依附在空间结构上行走移动的组装机器人,在设计其运动步态时应使其加速度尽量小并避免运动步频与结构固有频率的两倍相近.同时,在保障运动安全稳定的前提下尽可能减小抬起高度和运动步长.此外,机器人通过步态轨迹优化有效抑制了结构振动.下一步将研究空间结构表面移动机器人与大型柔性结构之间的分布式协同振动控制问题.