基于有限元压缩方法的复合材料RVE 创建1)
田文龙 齐乐华 晁许江
* (西北工业大学机电学院,西安 710072)
† (西北工业大学深圳研究院,广东深圳 518057)
引言
复合材料具有低密度、优异的力学性能(高比强度、高比刚度、低热膨胀系数和良好的耐磨性能等)及物理性能(优良的导电、导热和减振性能等),在航空、航天、国防和汽车等领域得到广泛的应用[1-5],例如在著名的双发宽体远程客机空客A350和波音Boeing787 中使用的复合材料的体积和质量占比分别达80.0%和50.0%.因此,准确表征复合材料的热-力学性能,建立其微观结构与热-力学性能的映射关系,具有非常重要的科学研究意义和工程应用价值,既可以为其工程应用提供理论指导,还有利于其微观结构优化及制备成形.
实验测试法具有设备昂贵复杂、测试周期较长和不能得到复合材料微观变形场等缺点[6],而传统分析方法不能充分考虑复合材料复杂的微观结构[7-8],因此数值方法常被用来预测复合材料的热-力学性能.数值方法既可以充分地考虑复合材料复杂的微观结构、准确地预测复合材料的热-力学性能,还能够提供复合材料各组分的微观变形信息.当采用数值方法预测复合材料热-力学性能时,首先需要创建能够准确表征复合材料微观结构的代表性体胞单元(RVE),而本文的侧重点就在于复合材料RVE 的创建方法.
目前,复合材料RVE 的创建方法主要包括以下3 类: (1)增强体非接触类方法,包括随机顺序吸附(RSA)法[9-10]和基于分子动力学(MD)的方法[11-12]等;(2)增强体相交移除类方法,主要是增强体迁移法[13-14];(3)基于图像三维重构技术的方法[15-16].基于图像三维重构技术的方法通过采用X 射线断层摄影技术和三维图像分析技术获取复合材料微观结构的层析图像,然后使用专业的软件重构出复合材料RVE.该类方法创建的复合材料RVE 与真实的复合材料微观结构非常接近,然而却需要昂贵、复杂的实验设备和专业的软件,且重构过程非常复杂,导致其应用范围较小.由于原理及执行算法的简单,RSA 法是前述提到的复合材料RVE 创建方法中应用最广泛的方法.然而,该类方法生成的复合材料RVE 中增强体体积分数存在特定的极限值(jamming limit)[17],同时创建增强体数量较多的复合材料RVE 时执行效率较低,且无法控制复合材料RVE 中增强体的取向分布.基于MD 法的复合材料RVE 创建方法可以创建较高增强体体积分数的复合材料RVE 及提高复合材料RVE 创建效率.然而,该类方法的数值执行算法非常复杂,同时也无法控制复合材料RVE 中增强体的取向分布.增强体迁移法能够创建具有高增强体体积分数的复合材料RVE、提高复合材料RVE 的创建效率及控制复合材料RVE 中增强体的取向分布,然而目前文献中报道的该类方法只能创建复合材料非周期性RVE,且创建增强体数量较多的复合材料RVE 时执行效率也较低.
近年来,相关学者提出了一种新型增强体非接触类复合材料RVE 创建方法,即有限元压缩方法[18-19]:首先创建具有较低增强体体积分数的复合材料RVE,然后采用有限元方法对其进行压缩,获取具有较高增强体体积分数的复合材料RVE.有限元压缩方法简单、高效,并且具有创建较高增强体体积分数复合材料RVE 的能力.Islam 等[18]将RSA 算法和有限元压缩方法相结合,创建了体积分数高达50.0%和大长径比的随机纤维增强复合材料的RVE(其他RVE 创建方法很难达到).为创建平面纤维增强复合材料的RVE,Zhang 等[19]结合虚拟填装算法和有限元压缩方法,创建了纤维体积分数高达45.0%复合材料的RVE,且在纤维动态压缩过程中基本不改变其取向分布.然而,有限元压缩方法目前还无法创建复合材料周期性RVE.
为创建具有较高增强体体积分数的复合材料周期性RVE,本文提出一种改进型有限元压缩方法,该方法主要包括3 个步骤: (1)利用RSA 算法生成具有较低体积分数的复合材料周期性RVE;(2)基于周期性边界条件和有限元压缩方法得到有限元网格格式、具有较高体积分数的复合材料周期性RVE;(3)后处理有限元模拟结果以得到复合材料周期性RVE 中所有增强体的位置及取向,进而创建CAD格式、具有较高体积分数的复合材料周期性RVE.采用提出的改进型有限元压缩方法成功创建了球形增强体复合材料的周期性RVE,其中增强体体积分数可达50%;然后,利用第1,2 和3 阶最近邻距离的概率分布函数[20]和最近邻取向角的累积概率分布函数[17]、Ripleys-K函数K(r)[17]和对关联函数G(r)[21]来表征创建的复合材料周期性RVE 中增强体的分布;最后,基于创建的复合材料周期性RVE和有限元均质法预测复合材料的弹性性能,并与实验测试和双夹杂模型[22]预测的结果进行对比,验证提出的改进型有限元压缩方法的有效性.
1 复合材料RVE 创建方法
本文提出一种用于创建具有较高增强体体积分数的复合材料周期性RVE 的有限元压缩方法,该方法的示意图如图1 所示,主要包括3 个步骤: (1)采用改进的RSA 算法创建具有较低增强体体积分数的复合材料周期性RVE;(2)在周期性边界条件的约束下,采用有限元方法压缩第1 步创建的较低增强体积分数的复合材料周期性RVE,以得到有限元网格格式、具有较高增强体体积分数的复合材料周期性RVE;(3)对第2 步的有限元模拟结果进行后处理,得到复合材料周期性RVE 中所有增强体的位置及取向,然后创建CAD 格式、具有较高增强体体积分数的复合材料周期性RVE.

图1 基于有限元压缩方法的复合材料周期性RVE 创建过程示意图Fig.1 Schematic diagram of the generation process of periodic RVE of composites using the FE compression method
本文后续将以球形增强体复合材料RVE 为研究对象,详细介绍提出的有限元压缩方法的基本原理.
1.1 复合材料稀疏RVE 创建方法
由于RSA 算法具有原理简单和执行效率高(当RVE 中增强体体积分数较低时)的优点,本文采用改进RSA 算法创建具有较低增强体体积分数的复合材料周期性RVE,其主要步骤如下:
(1) 创建尺寸为 [-1.5L,1.5L]×[-1.5L,1.5L]×[-1.5L,1.5L](L表示最后得到的复合材料周期性RVE 的边长)的基体(注意: RVE 的中心点为全局坐标系xyz的原点o);
(2) 在基体范围内随机(位置随机)生成一个球形增强体Ec;
(3) 检查增强体Ec是否超出基体的边界,若超出,则在基体的对应位置创建其周期性镜像Ep;否则,进行下一步操作;
学校发展亦或教改中都存在很多实际问题,面临种种实际困难。这些问题本身既是问题又是契机,我们必须以问题为导向,抓住学校发展的困难以及各学科独特的困难,这样才能精准发力。
(4) 检查增强体Ec及其周期性镜像Ep与基体中已存在的增强体Ei是否相交,若不相交,则在基体中保留增强体Ec及其周期性镜像Ep;否则,删除增强体Ec及其周期性镜像Ep,并返回第2 步;
(5) 重复执行第(2)~(4)步,直至基体中增强体体积分数或数量达到预设值.
在创建上述复合材料周期性RVE 过程中,需要保证后续添加的增强体(及其周期性映像)与基体中已存在的增强体之间不能发生相交,即
式中,rc ,rp和ri分别表示后续添加的增强体Ec、其周期性镜像Ep和基体中已存在的增强体Ei的中心,R表示增强体的半径,ξ是预设置的增强体间最小分离距离[23].同时,若后续添加的增强体超出基体边界,则在基体相应的位置创建特定数量的周期性镜像.对于增强体Ec,其周期性镜像Ep的数量Np及位置rp可以由下述方法确定.

图2 复合材料RVE 基体表面标号示意图Fig.2 Planar and vertex notations of an RVE of composites
在采用RSA算法创建复合材料RVE的过程中,最耗时的步骤是后续添加的增强体(及其周期性映像)与基体中已存在的增强体之间相交状态的判断.若基体中存在N个增强体,则后续添加的增强体(及其周期性映像)与基体中已存在的增强体需要进行o(N)次相交判断.若在RSA算法中引入能够减少增强体之间相交判断次数的算法,则可以提高RSA算法创建复合材料RVE的效率.对于后续添加的增强体Ec(及其周期性映像Ep),它们仅可能与其附近的增强体发生相交,因此本文引入RVE分区算法[24],以排除基体中肯定不与增强体Ec(及其周期性映像Ep)发生相交的增强体,进而提高RSA算法创建复合材料周期性RVE的效率.
在RVE 分区算法中,基体被分割成Nc×Nc×Nc个尺寸大于增强体直径的子区域;然后,根据分割的子区域与基体已存在的增强体之间的相交关系,将基体已存在的增强体分配到不同的子区域中;接下来,采用类似的方法,将后续添加的增强体Ec(及其周期性镜像Ep)分配到相应的子区域中;最后,只需判断增强体Ec(及其周期性镜像Ep)与包含增强体Ec(及其周期性镜像Ep)的子区域中的增强体之间的相交关系.注意,单个增强体可以被分配到多个子区域中(最多可达8 个).
1.2 复合材料稠密RVE 创建方法
在上述的有限元模拟中,增强体被设置为离散刚体,而RVE 的表面被设置为解析刚体,则采用三维4 节点双线性刚性四边形单元(Abaqus/Explicit中的单元类型为R3D4,每个节点具有3 个平移自由度和3 个旋转自由度)对增强体进行离散.为准确模拟增强体之间的接触,需将增强体离散成足够数量的单元,在本文中增强体的网格尺寸s选择为s=R/5.为考虑增强体之间的接触,本文采用面-面接触算法[18],其中接触发生在两个方向上: 切向和法向(垂直于接触表面).对于法向接触,采用“硬”接触算法来保证零穿透及增强体之间接触压力的传递;对于切向接触,采用库伦摩擦算法来保证增强体表面的相对滑动,摩擦系数选择为0.3.此外,为了实现复合材料RVE 压缩过程的准静态模拟,分析(压缩)步的时间分别选择为 200 s,最小增量步长选择为0.1 s,增强体的质量设置为 1.0 kg.
复合材料RVE 通常都是周期性的,在采用数值均质法预测复合材料热-力学性能时,这有利于施加周期性边界条件[25-26].为了生成复合材料周期性RVE,需将穿过基体边界的增强体复制并平移到基体的相应位置.因此,本文开发了一种基于周期性边界条件约束的有限元压缩方法创建具有较高增强体体积分数的复合材料周期性 RVE,即对于增强体(Ei) 及其周期性镜像 (Ep) 采用下述周期性边界条件进行约束.
1.3 CAD 格式复合材料RVE 创建
提出的有限元压缩方法创建的复合材料周期性RVE 中增强体以R3D4 单元的形式存在,需要将其转换为CAD 格式的复合材料周期性RVE,以便用于预测复合材料的结构和功能性能.因此,本文通过开发两个Abaqus Python API 脚本来自动检测基于有限元压缩方法得到的复合材料周期性RVE中增强体的中心点和创建CAD 格式的复合材料周期性RVE.注意: 在较低增强体体积分数的复合材料RVE 的压缩过程中,偶尔会出现一定数量(常小于10 对)的增强体相交现象,此时需要手动删除这些相交增强体.
2 结果与讨论
2.1 复合材料周期性RVE 中增强体分布统计
基于提出的有限元压缩方法,分别创建了增强体体积分数分别为 30.0%,40.0%和 50.0%的复合材料周期性RVE (如图3 所示,增强体的数量分别为579,764 和955),其中基体的尺寸为L=100.0 μm、增强体的半径为R=5.0 μm 和最小分离距离为 ξ=0.05R.在这一部分,本文将分别采用第1、第2 和第3 阶最近邻距离的概率分布函数[20]和最近邻取向角的累积概率分布函数[17]、Ripleys-K函数K(r)[17]和对关联函数G(r)[21]来表征创建的复合材料周期性RVE 中增强体的分布规律.

图3 基于提出的有限元压缩方法创建的增强体体积分数分别为30.0%,40.0%和50.0%的复合材料周期性RVEFig.3 Periodic RVEs of composites with inclusion volume fractions of 30.0%,40.0% and 50.0% generated using the proposed FE compression method
增强体Ei的 第n阶最近邻距 离dnth定义为该增强体中心点到它的第n阶最近邻增强体中心点的距离,而增强体Ei的第n阶最近邻取向角 θnth和 φnth定义为该增强体中心点到它的第n阶最近邻增强体中心点的连线与z轴的夹角和该增强体中心点到它的第n阶最近邻增强体中心点的连线在xoy平面的投影与x轴的夹角.图4 和图5 给出了创建的复合材料周期性RVE 中增强体的第1、第2 和第3 阶最近邻距离的概率分布函数和最近邻取向角的累积概率函数,可以发现: 第1 阶最近邻距离的概率分布函数曲线初始非常尖锐,然后快速下降,第2 和第3 阶最近邻距离的概率分布函数曲线相对平滑,而最近邻取向角 θ和 φ的累积概率函数曲线与增强体空间随机分布的理论累积概率函数曲线(Ψ(θ)=(1-cosθ)/2和 Ψ (φ)=φ/(2π))非常接近.因此,基于提出的有限元压缩方法创建的复合材料周期性RVE 中增强体空间随机(CSR)分布.

图4 复合材料周期性RVE 中增强体的第1、第2 和第3 阶最近邻距离的概率分布函数Fig.4 Probability distribution functions of the 1st,2nd and 3rd nearest neighbor distances of the inclusions in the generated periodic RVEs of composites


图5 复合材料周期性RVE 中增强体的最近邻取向角的累积概率分布函数Fig.5 Cumulative probability distribution functions of the 1st,2nd and 3rd nearest neighbor orientation angles of the inclusions in the generated periodic RVEs of composites
Ripleys-K函数K(r) 计算半径为r的搜索球中包含的增强体中心点的数量与创建的复合材料周期性RVE 中的增强体中心点密度的比值,即
式中,N表示创建的复合材料周期性RVE 中的增强体中心点的数量,V是创建的复合材料周期性RVE的体 积,κij表 示增强体Fi和Fj中心点之 间的距离.对于I(·),若括号中的条件为真,则I(·)的取值为1.0,否则I(·) 的取值为0.对于 ω (ri,rj),若中心点为ri,半径为 |ri-rj|的球完全包含于创建的复合材料周期性RVE,则 ω (ri,rj)返回数值1.0,否则返回包含在创建的复合材料周期性RVE 中球的体积比例.当创建的复合材料周期性RVE 中增强体空间随机分布时,Ripleys-K函数K(r) 的计算公式为Kν(r)=4πr3/3.对关联函数G(r)计算在距离给定的增强体中心点为r范围内找到另一个增强体中心点的概率,通常被视为Ripleys-K函数的空间导数[21],因此具有下述形式的表达式
式中,G(r)=1.0表示创建的复合材料周期性RVE 中增强体的分布符合CSR 分布.创建的复合材料周期性RVE 中增强体的Ripleys-K函数K(r)和对关联函数G(r)见图6 和图7.可以发现: 随着搜索半径r的增加,Ripleys-K函数K(r) 和对关联函数G(r)的曲线逐渐趋于曲线Kν(r)=4πr3/3 和G(r)=1.0.因此,可以得到下述结论: 基于提出的有限元压缩方法创建的复合材料周期性RVE 中增强体空间随机分布.

图6 复合材料周期性RVE 中增强体的Ripleys-K 函数K(r)Fig.6 Ripleys-K function of the inclusions in the generated periodic RVEs of composites

图7 复合材料周期性RVE 中增强体的对关联函数G(r)Fig.7 Pair correlation function G(r) of the inclusions in the generated periodic RVEs of composites
2.2 基于RVE 的复合材料弹性性能预测
在这部分,基于前述创建的复合材料周期性RVE,采用有限元均质方法[27-28]和周期性边界条件[25-26]对随机分布球形增强体复合材料的弹性性能进行数值预测.复合材料周期性RVE 的尺寸为L/R=20.0,网格单元选择4 节点四面体单元(即Abaqus/Standard中C3D4 单元),网格尺寸选为l=R/10.需要说明的是,上述给定的复合材料周期性RVE 和网格的尺寸可以保证得到收敛的复合材料弹性性能.
研究的第1 类SiC/Al 复合材料由2080 铝合金基体和随机分布的球形碳化硅(SiC)增强体组成[29],其中基体和增强体的各向同性弹性模量和泊松比分别为E0=74.0 GPa,ν0=0.33 和E1=410.0 GPa,ν1=0.19.研究的第2 类复合材料是球形氢氧化铝颗粒增强PMMA,其中氢氧化铝颗粒的体积分数、弹性模量和泊松比分别为v1=0.48,E1=70.0 GPa和 ν1=0.24,而PMMA 的弹性模量和泊松比分别为E0=3.5 GPa 和 ν0=0.31[30].研究的第3 类复合材料是球形玻璃颗粒增强树脂基复合材料[31],其中玻璃颗粒和树脂基体的弹性模量和泊松比分别为E0=74.0 GPa,ν0=0.33 和E1=410.0 GPa,ν1=0.19.
基于前述创建的复合材料周期性RVE,采用有限元均质方法和周期性边界条件预测的增强体体积分数为 50.0%SiC/Al 复合材料的刚度矩阵如下(单位GPa)
因此,可以得到该复合材料的弹性模量、剪切模量和泊松比,发现E1≈E2≈E3, ν12≈ν21≈ν13≈ν31≈ν23≈ν32和G12≈G13≈G23,则可以确定该复合材料的弹性性能是宏观各向同性的,原因在于该复合材料中增强体的空间随机分布.后续研究中,我们将使用宏观各向同性的弹性模量E、剪切模量G和泊松比 μ表征随机分布球形增强体复合材料的弹性性能.
基于创建的不同增强体体积分数的SiC/Al 复合材料周期性RVE、采用有限元均质方法预测该复合材料的弹性性能,并与实验测试结果[29]和双夹杂模型[22]的预测结果进行对比(见图8),发现有限元均质方法预测的该复合材料的弹性性能与实验测试和文献给出的结果及双夹杂模型的预测结果偏差很小.同时,基于有限元均质方法预测了的颗粒体积分数为0.48 的氢氧化铝/PMMA 复合材料弹性模量为E=11.06 GPa,与实验测试的该复合材料的弹性模量(E=10.4 GPa)[30]对比,可以发现两者之间的相对偏差小于6.35%.对于不同颗粒体积分数的玻璃/树脂基复合材料,基于有限元均质方法预测和实验测试的复合材料的弹性性能如表1 所示,发现有限元均质方法预测的该复合材料的弹性性能与实验测试结果吻合良好.
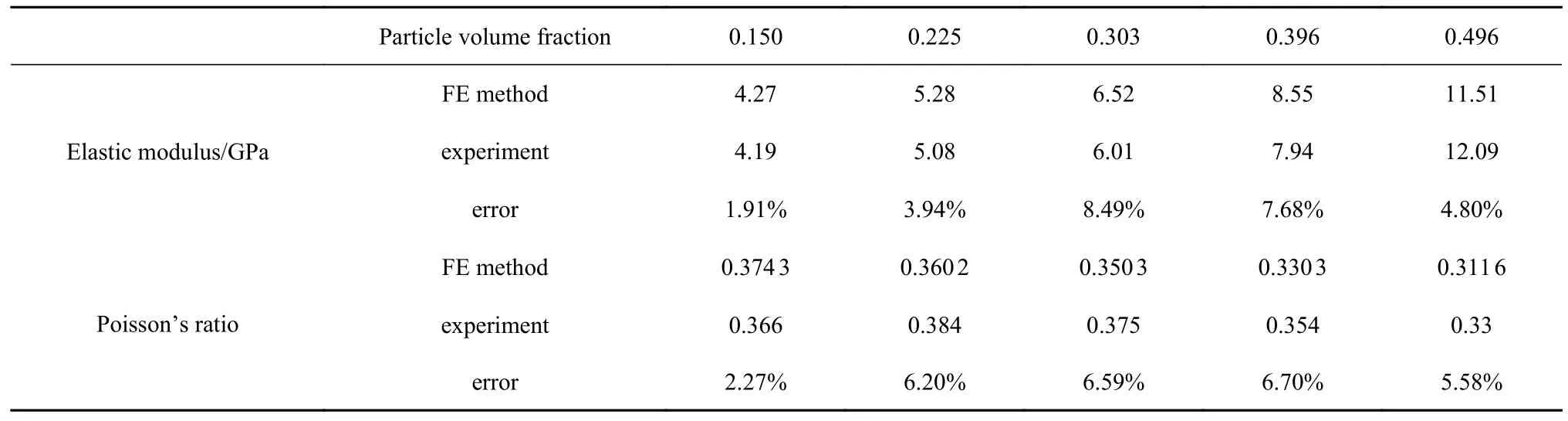
表1 基于有限元均质方法预测和实验测试的玻璃颗粒增强树脂复合材料的弹性性能[31]Table 1 Elastic properties of glass particles reinforced polymer composites predicted using the FE homogenization method and the experimental tests[31]

图8 基于有限元均质方法、双夹杂模型和实验测试得到的不同增强体体积分数SiC/Al 复合材料的弹性性能Fig.8 Elastic properties of SiC/Al composites with different inclusion volume fractions using FE homogenization method,double-inclusion model and available experimental tests
因此,创建的复合材料周期性RVE 可以用于准确预测随机分布球形增强体复合材料的弹性性能,则验证了本研究提出的有限元压缩方法创建复合材料周期性RVE 的有效性.
3 结论
为了简便、高效地创建具有较高增强体体积分数的复合材料周期性RVE,本文提出了一种改进型有限元压缩方法.基于提出的多步有限元压缩方法,成功创建了不同增强体体积分数的随机分布球形增强体复合材料的周期性RVE.然后,采用最近邻距离的概率分布函数、最近邻取向角的累积概率分布函数、Ripleys-K函数和对关联函数对创建的复合材料周期性RVE 中增强体的分布进行统计.最后,基于创建的复合材料周期性RVE,采用有限元均质方法和周期性边界条件预测了球形增强体复合材料的弹性性能,并与实验测试、文献给出和双夹杂模型预测的结果进行对比,验证创建的复合材料周期性RVE 及提出的有限元压缩方法的有效性.本研究的结论如下.
(1)提出的改进型有限元压缩方法的具体步骤如下: 生成具有较低增强体体积分数的复合材料周期性RVE;在周期性边界条件约束下,采用有限元方法压缩第1 步创建的复合材料周期性RVE,得到具有较高增强体体积分数的复合材料周期性RVE;通过后处理得到复合材料周期性RVE 中所有增强体的位置,进而创建CAD 格式的高增强体体积分数的复合材料周期性RVE.
(2)采用提出的改进型有限元压缩方法,成功创建了体积分数达50.0%的球形增强体复合材料的周期性RVE;基于第1、第2 和第3 阶最近邻距离的概率分布函数和最近邻取向角的累积概率分布函数、Ripleys-K函数和对关联函数对创建的复合材料周期性RVE 中增强体的分布进行统计,发现创建的复合材料周期性RVE 中球形增强体空间随机分布.
(3)基于有限元均质方法预测的复合材料弹性性能与实验测试和文献给出的结果及双夹杂模型的预测结果偏差很小,说明创建的复合材料周期性RVE可以用于准确预测复合材料的弹性性能,验证了提出的有限元压缩方法创建复合材料周期性RVE 的有效性.

