磁驱动中心对称挠曲电夹层板力电耦合性能分析1)

郭子文 章公也 糜长稳

(东南大学土木工程学院,南京 210096)

引言

力电耦合效应是广泛存在于各类电介质材料中的多场耦合效应之一,常见的形式有压电效应、电致伸缩效应、铁电效应等[1-5].一些线性力电耦合效应,如压电效应和挠曲电效应,由于可以实现电能和机械能之间的相互转化而被广泛应用于多种机电器件和设备中,例如谐振器、传感器、发电机和滤波器等[6-10].

挠曲电效应是电介质中应变梯度(非均匀应变)与电极化之间的耦合(正挠曲电效应),或者电极化梯度与应力的耦合关系(逆挠曲电效应).正挠曲电效应将机械能转化为电能,可用于制造传感元件或发电元件.逆挠曲电效应能够将电能转化为机械能,可应用于制造驱动元件.在传统压电材料中,均匀应变(如单轴拉压)能够通过压电效应激发电极化,其中,非中心对称晶体是材料表现压电性的必要条件;而挠曲电效应即使在中心对称晶体中,也可通过非均匀应变(如弯曲变形)局部破坏材料内部正负电荷的对称性并诱发挠曲电极化.近年来,挠曲电效应逐渐引起了研究者们的广泛关注.相比于压电效应,挠曲电效应具有明显的优势.一方面,压电效应仅存在于20 种非中心对称的介电材料中,这极大限制了压电材料的进一步发展与应用.而非均匀应变能够在所有介电材料中产生电极化,即挠曲电材料的来源比压电材料更广泛.另一方面,由于压电材料在高于居里温度时会发生相变,导致材料对称性增高,压电性消失,因而压电效应很难应用于高温场合,而挠曲电效应没有这个限制,故挠曲电材料的工作温度范围更广.除此之外,挠曲电效应会随着尺度的降低而急剧增强,当材料特征尺寸达到微纳米量级时,挠曲电效应会变得十分显著,因此在微纳米材料中挠曲电效应变得更加不可忽视[11-12].

在考虑挠曲电效应的连续介质力学模型中,机械载荷引起的弯曲变形和曲率引起的挠曲电极化是大多数研究人员关心的问题[13-20].除此之外,利用热弹性、热电性或磁致伸缩效应引起的热或磁致变形和电极化在多场耦合领域也已得到广泛应用[21-24].特别地,与直接施加机械载荷相比,利用磁电耦合材料进行磁调控是一种非接触式的智能驱动方法,通常出现在以压磁性材料作为驱动器的复合结构中,能够实现磁-力-电的多场耦合.磁电耦合材料具有很多重要的应用,包括磁传感器、数据存储、医学中的远程药物传递和无线能量采集器等[25-27].虽然自然界中的磁电耦合单相材料确实存在,如BiFeO3,Cr2O3和YMnO3,但是,它们具有较低的居里温度并且在室温下的磁电耦合性能很弱,这无疑限制了磁电耦合材料的应用[25].为此,人们转而采用压电和磁致伸缩复合结构,用以规避单一构型磁电材料的缺点,如BaTiO3和CoFe2O4磁电复合材料[28]、PZT 压电陶瓷与稀土合金Terfenol-D 磁电复合材料等[29].近期,Li 等[30]针对一维非压电悬臂梁的研究表明,通过磁场也可以激发挠曲电极化,这进而拓宽了挠曲电器件的应用范围.

现有文献对于挠曲电效应的结构理论研究大多只针对弯曲和屈曲等静态问题,缺乏对于较为复杂的受迫振动等动态问题的研究,尤其是将磁场作为驱动源时的动态振动机制尚不明晰.有鉴于中心对称挠曲电介电材料在微纳米尺度下显著的力电耦合效应和磁场的非接触驱动特性,本文以具有单个挠曲电层和两个对称压磁层组成的夹层板为例,通过多物理场结构理论建模,研究夹层板在全局和局部磁场驱动下的动态力电耦合响应,以期为磁控机电器件的优化设计提供新的改进思路.

1 结构理论框架

从连续介质力学的角度看,对于特定的模型结构,可以将三维框架简化为一维的梁、杆或二维的板模型,再通过解析法对这些模型进行求解.因此,本节将基于Mindlin 发展的多物理场结构理论分析方法建立挠曲电夹层板的二维理论分析框架.

1.1 单层挠曲电板

如图1 所示的单层挠曲电薄板,长度和宽度分别为a和b,厚度为2h.采用直角坐标系 (x1,x2,x3),在外部横向力q(x1,x2)的作用下发生变形.根据Mindlin 结构理论假设,板内任意质点的位移可沿板的厚度方向按级数形式展开,其一阶截断的表达式为[31-32]

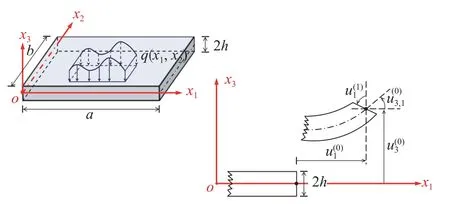
图1 单层板及采用的坐标系Fig.1 A single-layer plate and coordinate system

其中,φ(0)和 φ(1)表示沿板面的零阶电势和沿板横向的一阶电势.

根据经典偶应力理论[33-36],无穷小应变张量定义为 ε=(∇u+u∇)/2;曲率张量表达式为χ=θ ⊗∇,其中 θ(=(∇×u)/2) 为旋转矢量.结合式(1) 可得非0应变和曲率分量分别为

此外,静电场强度可由电势的负梯度计算得到,即E=-∇φ.结合式(2)可得其分量形式为

根据偶应力挠曲电理论[36-37],单层挠曲电板的Gibbs 自由能(G)在 [0,T]时间内的一阶变分为

对应于上式的本构方程为[38]

其中,Cijkl为挠曲电板的4 阶弹性刚度张量、sij为介电系数张量、fikl为3 阶挠曲电系数张量,反映电极化和曲率之间的力电耦合效应.

1.2 夹层板的三维本构关系

考虑图2 所示的三明治式压磁驱动挠曲电夹层板结构,该模型建立在直角坐标系 (x1,x2,x3)之中,由中间的挠曲电层和沿着挠曲电层的中面呈上下对称分布的两个压磁层组成.其中,挠曲电层选用具有中心对称的立方晶体结构(m3m 点群)材料,具有挠曲电性.压磁层选用具有横观各向同性的六方晶体结构(6mm 点群)材料,不含压电性和磁电耦合效应,仅考虑压磁性能.两侧六方晶体压磁层的c轴虽均沿x3方向,但是二者极化方向相反.在横向磁场H3作用下,当其中一个压磁层在面内由磁致伸缩效应产生拉伸变形时,另一个压磁层则会产生压缩变形,夹层板结构整体的拉压变形得以相互抵消,反之亦然.

图2 磁场作用下的夹层板模型Fig.2 A sandwich plate model under a magnetic field

对于立方晶体结构材料,挠曲电层的三维本构关系为[38]

对于横观各向同性结构材料,上部压磁层的三维本构关系为[39]

下部压磁层的c轴方向为负时,压磁系数的符号发生改变,因而其面内正应力本构方程变为

1.3 夹层板的控制方程和边界条件

对应的边界条件为

其中,ρ表示质量密度.式(13) 中的物理量建立在(n,s,x3)下,由坐标系(x1,x2,x3)转换得到[41].

将式(3)～式(5)、式(8)～式(10)代入式(13),再将所得二维本构代入式(11),可得到以位移,,,电势 φ(1)以及磁场强度H3表示的夹层板控制方程,即

其中

2 受迫振动分析

为了论证上节建立的挠曲电夹层板二维理论模型,本节将分别对其在全局和局部横向磁场作用下的动态力电耦合响应展开研究.以简支板闭合电路状态为例(边界配置如图3 所示),边界条件可根据式(12)得到,即

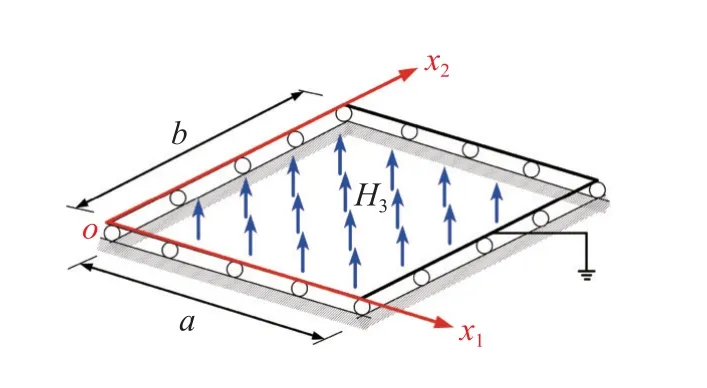
图3 横向磁场驱动下夹层板的边界配置Fig.3 Boundary configuration of sandwich plate under a transverse magnetic field

对于矩形板,沿x1=0 和x1=a,边界条件为

将二维本构代入式(18)可进一步得到

沿x2=0和x2=b,边界条件为

将二维本构代入式(21)可进一步得到

本节主要分析外部磁场对模型的驱动作用,不考虑体力项,即令.夹层板受到时谐磁场的作用,磁场强度表达式为

其中,ξm=mπ/a,ζn=nπ/b,ω是板的激振频率,i 是虚数单位并满足i2=-1.代表磁场强度正弦级数展开式的系数,可通过积分计算得到,即

取决于外加驱动磁场的形式,位移场和电势场也必然具有相应的时空分布特征,即

将式(23)和式(25)代入控制方程(14)得线性方程组

其中,Kij和Mij分别为4×4 的刚度矩阵和质量矩阵,二者的非零分量为

为了求解数值结果,本节选取的板尺寸参数为:h=10 nm,c=0.4h,a=b=40h.压磁层和挠曲电层材料分别选取CoFe2O4和Si,二者的物理参数如表1 所示[40,42].值得注意的是,由于CoFe2O4的挠曲电系数无法在现有文献中得出,本文忽略了压磁层的挠曲电效应[43].

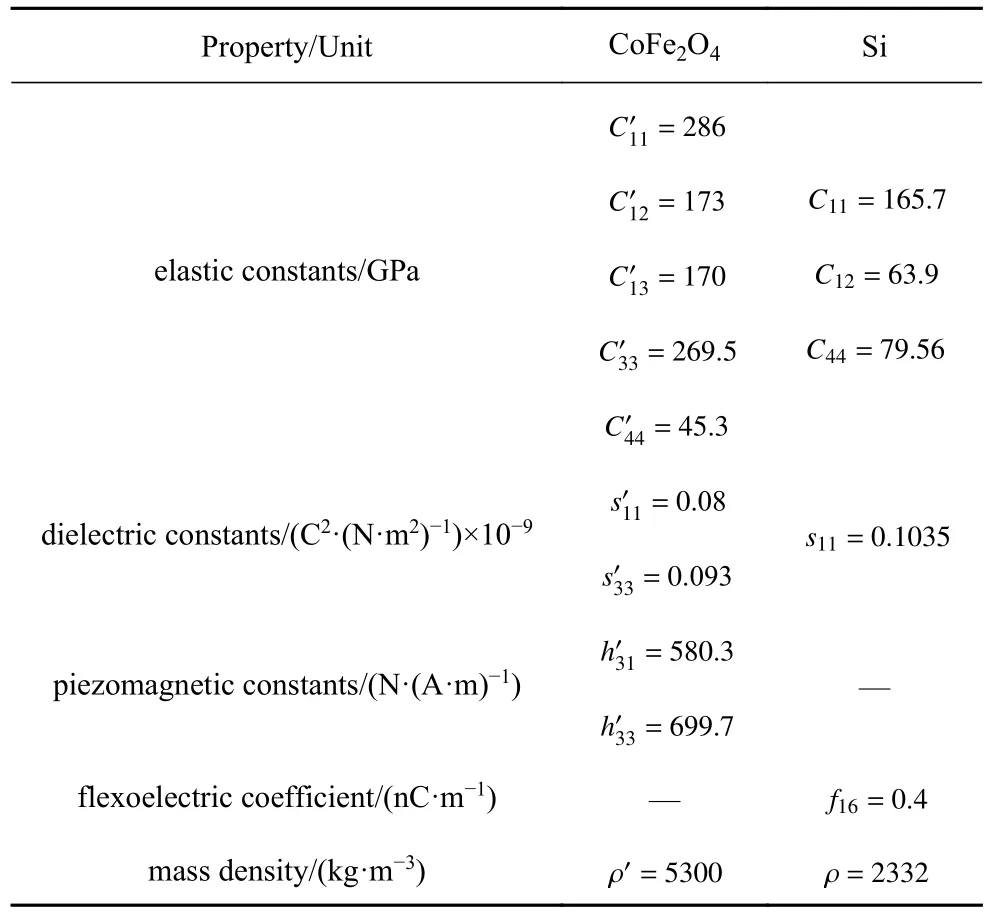
表1 CoFe2O4 和Si 的材料参数Table 1 Material parameters of CoFe2O4 and Si

2.1 全局磁场驱动

本小节研究全局磁场驱动下复合板的受迫振动问题,考虑幅值为h0=1.0×106A/m 的正弦型磁场强度分布形式

图4 展示了单侧压磁层驱动挠曲电双层板(蓝色线条)(参见文献[40])与当前夹层板模型(红色线条)在正弦型全局磁场驱动下的一阶电势幅频关系对比,两种模型的材料组分占比和几何尺寸均保持一致.从图中可以看出,一阶电势表现出明显的频率依赖性,当激振频率远离固有频率时,一阶电势的振动幅值几乎为零,而当激振频率靠近固有频率时,一阶电势的振动幅度急剧增加,在固有频率处达到最大值.此外,相较于“双层复合板”、“当前夹层板”的一阶电势明显增大,峰值提高了10%以上,这表明对称式驱动压磁层分布方式趋于提高多层复合板的力电耦合性能.

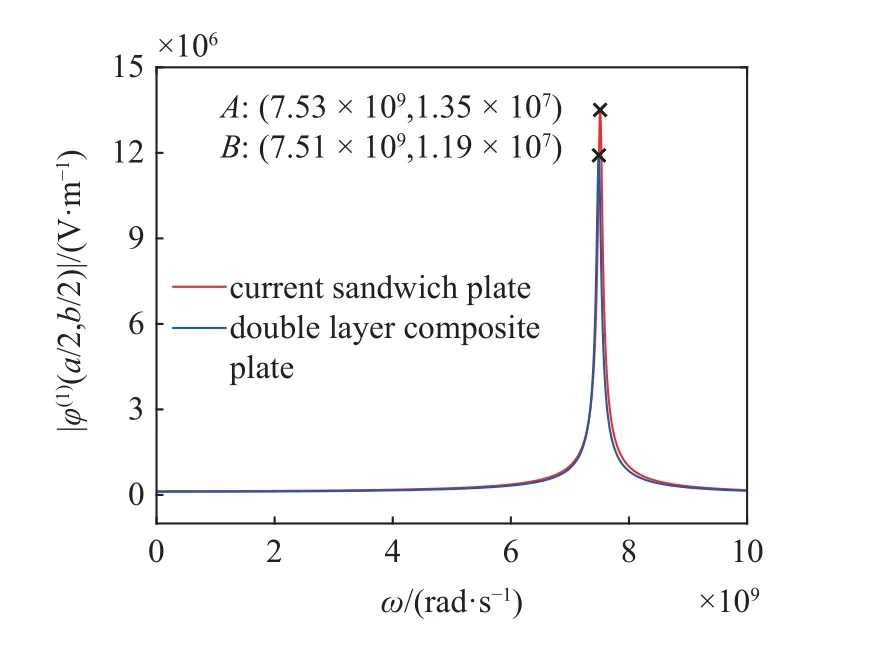
图4 全局磁场驱动下的一阶电势幅频关系对比Fig.4 Comparison of amplitude-frequency curve of first-order potential under the global magnetic field

2.2 局部磁场驱动

本小节采用H3=h0exp(iωt)的均布局部磁场驱动复合板,磁场的驱动范围是一个长度为2d(d＜a/2),宽度为2e(e＜b/2)的矩形区域,如图5 所示的灰色区域,关于矩形板的中心(x0,y0)对称.对于该均布局部磁场,式(24)中的傅里叶系数可计算为

图5 局部驱动磁场作用区域(灰色区域)Fig.5 Local magnetic field area (grey area)

局部磁场的具体驱动范围可通过改变d和e进行调整,为了便于进行数值计算,本小节取d=e=25 nm.

图6 展示了局部磁场驱动下复合板的挠度振动幅值与激振频率关系,其中,h0=1.0×106A/m.在式(23) 中共保留了30 项,此时的计算结果与保留60 项时在小数点后第3 位依然一致,表明在驱动磁场的傅里叶级数中取30 项可以满足收敛性要求.从图6 中可以看出,在0～5.0×1010rad/s 的激振频率范围内,一共出现了3 阶固有频率,相应产生了3 个共振峰,并且,随着固有频率的增加,共振峰值越来越低.受到复合板振动阻尼的影响,固有频率不再表现为单一的频率值,而是表现为一小段固有频率区间.

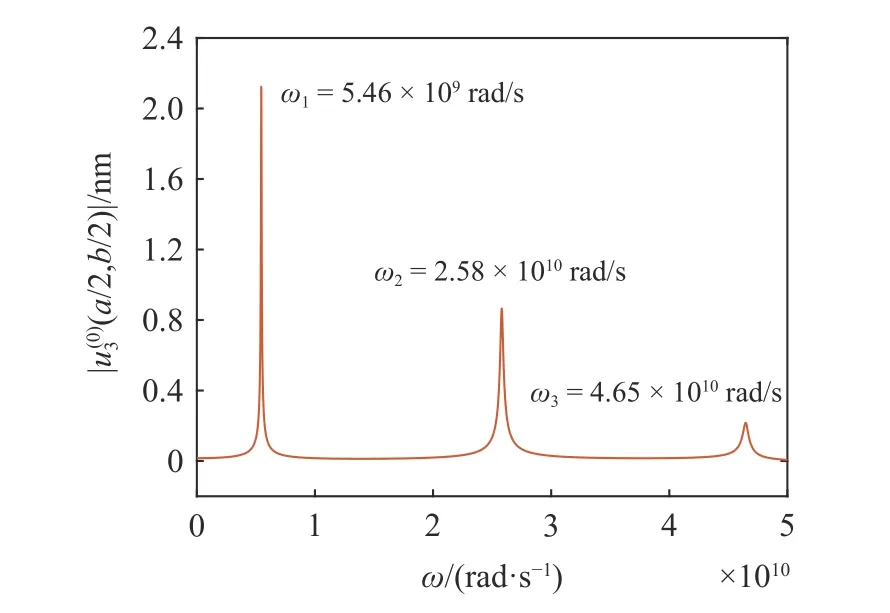
图6 局部磁场驱动下夹层板的挠度幅频关系Fig.6 Deflection amplitude-frequency curve of the sandwich plate under local magnetic field

与图6 的前两阶固有频率相对应,图7 给出了夹层板的挠度、转角和横向电势振型.虽然这些振型实际上是复值,但由于它们的虚部远小于实部,因此可略去虚部.由于矩形板几何尺寸和磁场作用范围的对称性,夹层板的转角的分布类似,出于简化的目的,的分布未做展示.从图7 中可以看出,这些振型具有很强的频率依赖性,低阶振型具有更大的振动幅值,而高阶振型沿复合板长度和宽度方向具有更短的周期.特别地,从图7(b)和图7(f)中还可以明显看出,由于磁场的局部驱动特征,在作用区域中心附近产生挠度、转角和电势峰值.图7所展示的结果对板型磁驱动器(磁能转换为机械能)和板型磁传感器(磁能转换为电能)的优化设计具有重要的参考价值.

图7 局部磁场驱动下夹层板的前两阶挠度、转角和一阶电势振型Fig.7 The first two order deflection,rotation angle and first-order potential mode of the sandwich plate under the local magnetic field

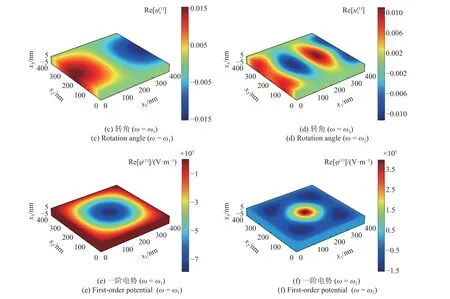
图7 局部磁场驱动下夹层板的前两阶挠度、转角和一阶电势振型 (续)Fig.7 The first two order deflection,rotation angle and first-order potential mode of the sandwich plate under the local magnetic field (continued)

3 结论

本文以探索新型磁控纳米机电器件为研究背景,提出了一种新的三明治式压磁驱动挠曲电夹层板模型,构建了夹层板的二维控制方程和边界条件,并分析了矩形简支板在全局和局部磁场激励下的动态力电耦合响应.基于本文的数值研究结果可以获得以下两点重要结论.

(1) 在外部时谐磁场驱动下,夹层板的位移和电势振动幅值依赖于激振频率.随着固有频率的增加,振型幅值迅速衰减,振型表现出周期变化特征.

(2) 驱动压磁层的分布方式对复合板结构的力电耦合响应具有重要影响,本文设计的对称式驱动压磁层分布方式趋于提高复合板的力电耦合性能.

本文的理论模型和研究结果可为磁控机电器件的优化设计提供新的改进思路.