利用不等式求最值常见题型的解法探讨
2023-08-04 07:37云南省昆明市石林县第一中学
中学数学 2023年15期
云南省昆明市石林县第一中学 王 强
利用不等式求最值的题型有很多,解法多种多样.有些题型可能有多种解法,但有些题型可能会令我们束手无策,怎样才能找到这些题型的解法呢?这就需要我们能够抓住题中的条件式、求值式的结构特征找到它们的解法!下面就以一些常见题型为例来探讨这些题型的解法.
1 题型一:条件式为二次式,求值式为一次式
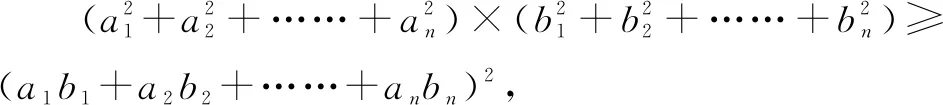
对于“已知x2+my2+kxy=p,求x+ny的最值”,可以先将条件式变形,再用柯西不等式,如例2.
例1已知x>0,y>0,且x2+2y2=9,则x+4y的最大值为.
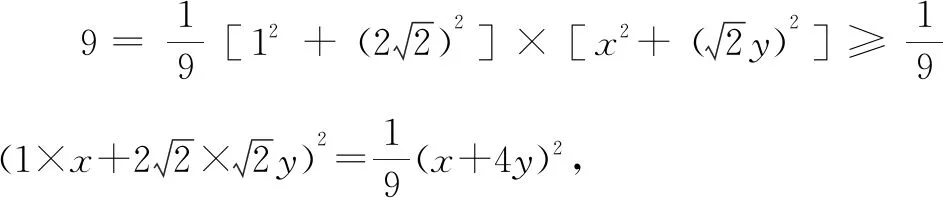
故x+4y的最大值为9.
方法点睛:利用柯西不等式降次,实现由条件式向求值式的转化.
例2已知实数x,y满足4x2+y2+xy=1,求4x+y的最大值.
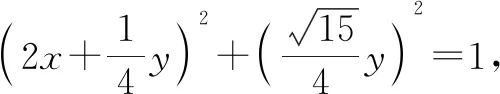
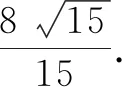
方法点睛:通过配方将条件式转化为两项平方和的形式,再用柯西不等式实现由条件式向求值式的转化.
2 题型二:条件式为一次式、二次式,求值式为分式且分母为一次式、二次式
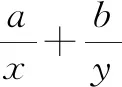
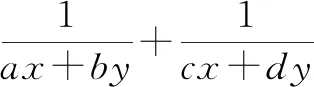
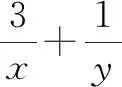
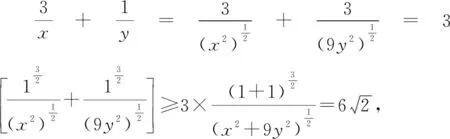
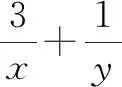
方法点睛:先对求值式的分母进行升次变形,再用权方和不等式实现求值式向条件式的转化.

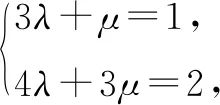


方法点睛:先找出条件式与求值式分母之间的关系,再用权方和不等式实现由求值式向条件式的转化.
3 题型三:求值式为齐次分式

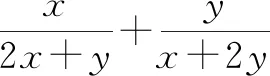

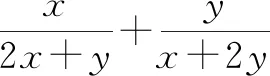
方法点睛:先化作比值,再将比值换元,实现由二元变量向一元变量的转化,再用均值不等式求最值.
4 题型四:求值式为和(积)的形式,条件式可变形为积(和)的形式
对于“求(x+m)+p(y+n)型式子的最值”,可以将已知条件变形为(x+m)(y+n)=k;对于“求(x+m)(y+n)型式子的最值”,可以将已知条件变形为(x+m)+p(y+n)=l.
例6已知0 故选答案:C. 上文结合具体实例探讨了利用不等式求最值常见题型的解法,但由于利用不等式求最值的题型比较多,特征也多种多样,解题方法也不只有上述几种,因此,我们应该在平常的解题过程中不断发现、积累,养成良好的解题习惯.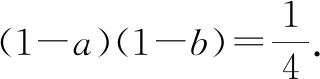
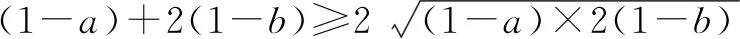
猜你喜欢
中学生数理化·七年级数学人教版(2021年11期)2021-12-06
中学生数理化·七年级数学人教版(2020年11期)2020-12-14
语数外学习·高中版中旬(2020年2期)2020-09-10
河北理科教学研究(2020年1期)2020-07-24
中学生数理化·七年级数学人教版(2019年11期)2019-09-10
小学生作文(低年级适用)(2017年11期)2017-12-20
新东方英语·中学版(2017年9期)2017-09-25
数理化解题研究(2017年4期)2017-05-04
环球人物(2017年3期)2017-03-31
中学生数理化·八年级数学人教版(2017年1期)2017-03-25

