第三定义创设,轨迹性质应用——基于几道教材习题的探究

江苏省吴江平望中学 潘妙妙

苏联数学教育家奥加涅相说过:“必须重视很多习题潜在着进一步扩展其数学功能、发展功能和教育功能的可行性.”特别是高中数学教材,是高中数学教学与学习的根源所在,也是高考命题的背景与根基.认真钻研教材,领悟教材的意图与内涵,对教学资源进行必要的整合与拓展是高中数学教学与学习的关键所在.

1 源于教材

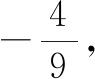
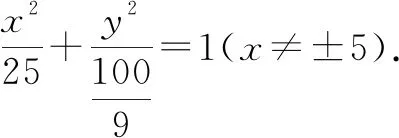
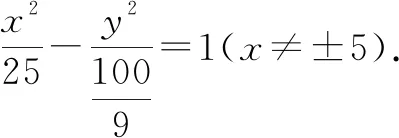
习题[普通高中数学必修一(人教A版)第三章“圆锥曲线的方程”中第146页复习参考题第11题]已知△ABC的两个顶点A,B的坐标分别是(-5,0),(5,0),且AC,BC所在直线的斜率之积等于m(m≠0),求顶点C的轨迹.

以上三道例(习)题研究的都是:平面上异于两定点的动点,其与两定点所构成的直线的斜率之积等于非零常数,根据常数取值的变化情况,对应的轨迹为椭圆(或双曲线)问题.而不同问题中具体常数的取值情况,与对应的轨迹(椭圆或双曲线)之间存在何种关系或对应联系呢?其是否与圆的方程之间存在某种关系?是否与初中学习过的涉及圆的圆周角定理、圆的垂径定理等存在某种关系?

2 探究拓展

以上展示的是求动点轨迹方程的问题,而问题实质与背景就是椭圆(或双曲线)的“第三定义”,以及与之对应的轨迹方程和相应的性质问题等.

2.1 第三定义

椭圆(或双曲线)第三定义:平面内与两个定点A(-a,0),B(a,0)连线的斜率的乘积等于常数e2-1的点的轨迹叫做椭圆(或双曲线).其中两个定点A(-a,0),B(a,0)分别为椭圆(或双曲线)的顶点.

当常数e2-1小于0且不等于-1时,对应动点的轨迹为椭圆;当常数e2-1大于0时,对应动点的轨迹为双曲线.

2.2 轨迹问题

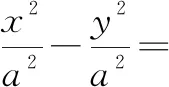
(1)若λ<-1或-1<λ<0,则动点P的轨迹为椭圆(除A,B两点外);

(2)若λ>0,则动点P的轨迹为双曲线(除A,B两点外);

(3)若λ=-1,则动点P的轨迹为圆(除A,B两点外).

2.3 性质问题

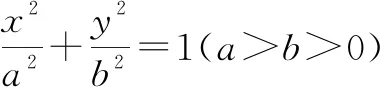
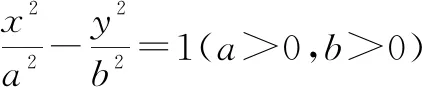
推论1(圆周角定理的推广)若AB为“有心圆锥曲线”(圆e=0,椭圆01)的“直径”(过对称中心的弦),M为曲线上异于点A,B的任意动点,则kAM·kBM=e2-1.

推论2(圆的垂径定理的推广)若M为“有心圆锥曲线”(圆e=0,椭圆01)的弦AB的中点,其中弦AB不过曲线中心O且不平行于对称轴,则kAB·kOM=e2-1.

3 链接高考

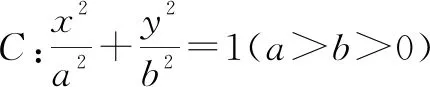
解析：设Q关于x轴的对应点为M,则kAP·kAQ=-kAP·kAM.

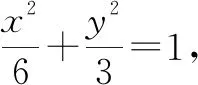
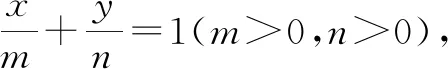
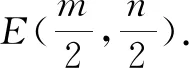
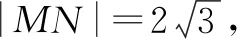
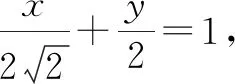
点评：高考题常常源于教材而高于教材,是在高中数学教材的基础上合理创设,并进一步加以变式拓展与能力提升,很好地考查学生的“四基”落实情况,以及数学能力与数学品质.

4 教学启示

4.1 回归教材,深挖内涵

教材中的例(习)题等,都是不同时期背景下教学与研究的精华与积累,具有很好的示范与引领作用.新高考命题方针下,更多的高考真题都出自高中数学教材中的例(习)题,借助教材中例(习)题加以背景创设、情境改编、变式应用、拓展提升等,并进一步综合此类例(习)题的背景、知识、思想、方法、技巧与策略等,既源于教材,又高于教材,充分体现了传承与发展.

4.2 以“本”为“本”,提升能力

在高中数学教学中,回归教材,以其为蓝本,以“本”为“本”,吃准吃透,链接教材前后相关知识,合理并正确构建起高中数学相关知识的网络体系与知识框架,不断挖掘数学知识的本源与内涵,渗透数学思想方法和核心素养,让平时的数学教学真正为高考提供有效的动力与能力支持,全面提升学生数学能力,促其养成良好的数学品质与习惯.