“数形结合”解简单指(对)数不等式

袁少军

(湖北省麻城市第二中学)

人教A 版数学教材《必修1》中介绍了一元二次不等式的解法,其中解含参数的不等式是一类重难点问题,教材也着重对该类问题进行了探究.但后续的学习中有关指数不等式、对数不等式的解法却没作重点研究,以至于在高二、高三导数的学习中,学生遇到有关不等式的问题时,困难重重,错误频出.

1 问题的呈现

此题得分偏低,解答中出现的错误很多,有的同学没有注意函数的定义域,有的同学没有进行分类讨论…… 我们先回顾一下一元二次不等式的求解过程:首先是将一元二次不等式化简整理为ax2＋bx＋c＞0(或ax2＋bx＋c＜0等)的规范形式,然后利用Δ＞0,求出对应方程的两个根x1,x2(不妨设x1＜x2),再结合对应的二次函数图像,在a＞0时,抛物线开口向上,最后可得解集{x|x＜x1或x＞x2},其余情形,这里不再赘述.总结起来,就是先寻找函数的零点,再结合函数的单调性和函数的图像得出不等式的解集.

2 系数为常数的指数不等式、对数不等式的解法

例1解下列不等式:

(1)ex－2＞0;

(2)1－2lnx＞0.

解析

(1)设函数f(x)＝ex－2,则f(x)的零点为x＝ln2,易知f(x)单调递增,则可作出f(x)的草图如图1所示,故所求不等式的解集为(ln2,＋∞).

(2)设函数g(x)＝1－2lnx,则g(x)的零点为,易知g(x)单调递减,且x∈(0,＋∞),则可作出g(x)的草图如图2所示,故所求不等式的解集为

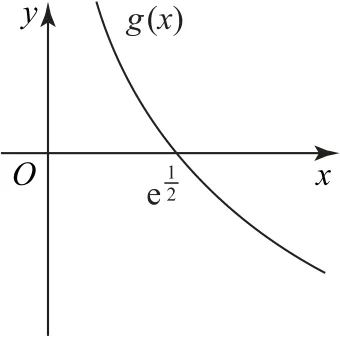
图2

点评

求解此类不等式的方法很多,此处所用的方法是先求函数零点,再判断函数的单调性,最后根据“数形结合”得出解集.

例2解下列不等式:

(1)(ex－1)(ex－2)＞0;

(2)(x－2)(ex－2)＜0.

解析

(1)方法1因为(ex－1)(ex－2)＞0,所以

方法2设函数f(x)＝(ex－1)(ex－2),则f(x)的零点为x1＝0,x2＝ln2,在每一个因式中ex的系数为正的条件下,作出f(x)的草图如图3所示,可得解集为(－∞,0)∪(ln2,＋∞).

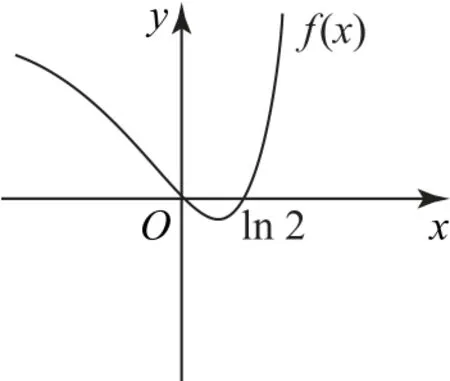
图3

方法2设函数g(x)＝(x－2)(ex－2),则函数g(x)的零点为x1＝2,x2＝ln2,在两个因式中x和ex的系数都为正的条件下,作出g(x)的草图如图4 所示,可得解集为(ln2,2).

图4

点评

方法1是通过分类讨论,将之转化成求解不等式组.方法2先将不等式进行因式分解,使每一项的系数为正,再求出对应函数的零点(即对应方程的根),然后在数轴上按大小顺序依次标根,最后从右往左、自上而下依次穿根得到解集.

3 含参数的指数不等式、对数不等式的解法

此类问题多见于导数解答题中的单调性讨论问题,如“指数函数与一次、二次函数联袂的函数”,还有“对数函数与一次、二次函数联袂的函数”.此类函数求导后的导函数常常是以下形式:(mx＋n)(aex＋b),(mx＋n)(alnx＋b).对于导函数为(mx＋n)·(aex＋b)(m,n为系数)形式的函数,我们较熟悉,此处不作讨论;对于a,b为参数时,可作如下分类讨论:

当a＝0时,导函数变为(mx＋n)·b,利用一次函数的性质讨论即可;

当a,b同号时,若导函数中的因式(aex＋b)恒为正或恒为负,讨论(mx＋n)即可;

当a,b异号时,设导函数(mx＋n)(aex＋b)的零点为x1,x2,再依据m,a的正负,对有关的不等式进行分类讨论即可.

例3已知函数f(x)＝aex－x－1(a∈R),试讨论函数f(x)的单调性.

解析

易知f(x)的定义域为R,且f′(x)＝aex－1.当a≤0时,f′(x)＝aex－1＜0恒成立,故f(x)在R上单调递减.

当a＞0时,令f′(x)＝aex－1＝0,可得导函数的零点为x＝－lna,此时f′(x)在a＞0的条件下单调递增,可作出f′(x)的草图如图5所示,则aex－1＞0的解集为(－lna,＋∞),故函数f(x)的单调递增区间为(－lna,＋∞);同理,aex－1＜0 的解集为(－∞,－lna),故f(x)的单调递减区间为(－∞,－lna).

图5

综上,当a≤0时,f(x)在R上单调递减;当a＞0时,f(x)的单调递增区间为(－lna,＋∞),单调递减区间为(－∞,－lna).

点评

求解有关导函数的不等式时,可以通过数形结合思想得出不等式的解集,从而写出正确的单调区间.

令f′(x)＝0,得x＝1或a.

当a＝1时,f′(x)≥0(当且仅当x＝1时,等号成立),故f(x)在(0,＋∞)上单调递增.

当0＜a＜1时,令f′(x)＞0,则(x－a)lnx＞0,此时两个因式中x和lnx的系数都为正的条件下,零点为x1＝1或x2＝a(x1＞x2),作出φ(x)＝(xa)lnx的草图如图6所示,可得出解集为(0,a)∪(1,＋∞);令f′(x)＜0,则(x－a)·lnx＜0,同理可得出解集为(a,1).

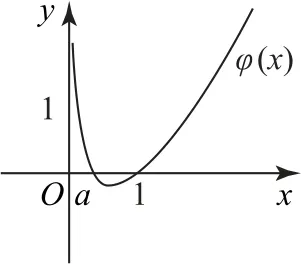
图6

当a＞1时,令f′(x)＞0,则(x－a)lnx＞0,此时两个因式中x和lnx的系数都为正的条件下,零点为x1＝1或x2＝a(x1＜x2),作出φ(x)＝(x－a)lnx的草图如图7 所示,可得出解集为(0,1)∪(a＋∞);令f′(x)＜0,则(x－a)lnx＜0,同理可得出解集为(1,a).

图7

综上,当a＝1时,f(x)在(0,＋∞)上单调递增;当0＜a＜1时,f(x)的单调递增区间为(0,a),(1,＋∞),单调递减区间为(a,1);当a＞1时,f(x)的单调递增区间为(0,1),(a,＋∞),单调递减区间为(1,a).

点评

此题中导函数有两个零点,类比一元二次不等式的“数轴标根法”,可以准确地写出导数不等式的解集,求出单调区间.

例5已知函数f(x)＝ae2x＋(1－2a)ex－x,讨论函数f(x)的单调性.

解析

函数f(x)的定义域为R,且

当a≥0时,2aex＋1＞0,故f(x)的单调递增区间为(0,＋∞),单调递减区间为(－∞,0).

(完)