高层建筑外附雨篷的表面风压和气动力系数
沈国辉 ,李懿鹏 ,韩康辉 ,余杭聪 ,邵剑文
(1.浙江大学 建筑工程学院,浙江 杭州 310058;2.浙江大学 平衡建筑研究中心,浙江 杭州 310028;3.浙江大学建筑设计研究院有限公司,浙江 杭州 310028)
高层建筑承载了办公、酒店、公寓等功能,在城市中得到广泛应用.雨篷位于高层建筑入口位置,为出入口行人提供遮阳避雨功能,同时也防止高空坠物对出入口行人造成伤害[1].高层建筑雨篷具有轻质、高柔等特点,风荷载是雨篷设计的主要控制荷载.
目前针对雨篷风荷载的研究主要集中在大型屋盖结构的悬挑雨篷上.沈国辉等[2]以某机场悬挑雨篷为例,分析悬挑屋盖的上下表面风压相关性,给出考虑相关性的围护结构风荷载计算方法;赵建华[3]针对北京南站雨篷进行风洞试验,获得不同风向角下的平均风压,发现负风压主要发生在迎风角区;孙建龙[4]针对3个大型火车站雨篷进行风洞测试,发现雨篷的整体风吸力系数约为-0.25;周晋芳[5]进行体育场看台多个倾角的风洞试验,分析特征湍流与风压非高斯特性之间的关系;Killen 等[6]分析平面几何形状、倾角和前沿广告牌等对悬挑屋盖风荷载的影响;Barnard[7]研究发现透风率对矩形悬挑平屋的脉动风压有显著影响;楼文娟等[8]采用风洞试验和CFD方法研究某体育场悬挑屋盖的风荷载,提出了在屋盖悬挑部分开洞的减压措施;康黎明[9]利用CFD方法研究悬挑屋盖的风荷载,分析了增设导流板和开设通风孔的气动措施.以上研究均主要针对大屋盖的悬挑结构,对高层建筑雨篷风压的研究几乎没有,而我国规范[10],以及澳大利亚/新西兰、美国、日本等国规范[11-13]均未给出高层建筑外附雨篷的风荷载规定.
基于以上背景,本文以高层建筑外附雨篷的风压分布为研究对象,研究了该雨篷的平均风压、脉动风压、上下表面风压相关性和测点风压的非高斯性,探讨外附雨篷整体升力系数随风向角的变化和时程的非高斯性特征,给出了围护结构的设计风压,最后分析了倾角和出挑长度对整体升力系数的影响.研究成果可为高层建筑外附雨篷的抗风设计提供参考.
1 高层建筑雨篷的风洞试验
1.1 试验概况和测点布置
调研高层建筑雨篷的设计案例[14],某实际雨篷尺寸为宽度20.3 m,悬挑长度11.235 m,离地高度7.65 m.确定本次试验基准雨篷的宽度W=20 m,高度H=10 m,悬挑长度D=12 m,倾角α=0°,如图1所示.将高层建筑设定为高100 m、宽50 m、厚30 m,以反映高层建筑对雨篷的气动干扰.雨篷的风洞试验如图2所示.

图1 雨篷的尺寸参数和风向角Fig.1 Dimensional parameter of canopy and wind azimuth

图2 雨篷的风洞试验照片Fig.2 Picture of canopy in wind tunnel test
模型的几何缩尺比为1∶100,雨篷模型的测点布置见图3,上下表面各布置160个测点,采用上下表面对应布置,风洞试验时对所有测点进行同步测压.不同倾角下的测点布置方案与基准雨篷是一致的,其他出挑长度情况下的测点布置相当于将基准雨篷的测点布置延长或缩短.由于整个模型具有对称性,试验风向角θ为0°~180°,风向角间隔为10°,共进行19个风向角的测试.

图3 雨篷的测点和风向角Fig.3 Measuring points of canopy and wind azimuth
1.2 风场模拟
风洞试验在浙江大学ZD-1边界层风洞中进行,采用B 类地貌,根据《建筑结构荷载规范》(GB 50009—2012)[10],B类地貌的平均风速V和湍流度I剖面如式(1)和式(2)所示.
式中:α为0.15;I10为0.14;V10为10 m 高度处的参考风速.风洞中利用尖劈和粗糙元模拟B 类地貌风场,平均风速和湍流度剖面如图4 所示,图中VR为参考点高度处的风速,图中还给出了规范的建议值,可以发现风洞模拟值与规范建议值吻合较好.
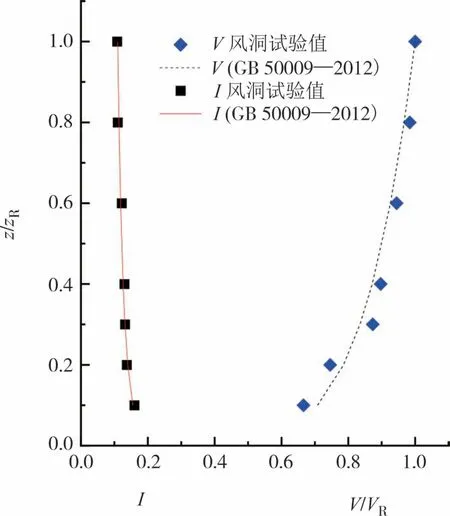
图4 风洞模拟的B类地貌Fig.4 Terrain category B simulated in wind tunnel
1.3 数据处理
测点的风压系数Cpi定义为:
式中:Pi为测点i的风压;P∞为参考点静压;ρ为空气密度;U∞为参考点的风速.选取雨篷高度作为风压系数的参考点,因此Cpi等同于荷载规范中的体型系数,试验中雨篷高度处的来流速度为10.4 m/s.
对于悬挑雨篷,上下表面的风压系数叠加时程Cpc按公式(4)计算.
式中:Cpu与Cpd分别对应测点的上、下表面风压系数时程;t为时间.
式中:γ为上下表面风压时程的相关系数,计算如下:
式中:Ai为i测点的控制面积;A为雨篷总面积;CF定义为垂直表面向上为正,垂直表面向下为负.
2 雨篷的平均风压系数
图5 给出了雨篷在0°风向角下的风压系数,分别给出了上表面、下表面和上下表面叠加数据.由图5可知:1)0°风向角下,雨篷上表面均为正压,由于气流受到后方高层建筑的阻挡,气流下翻导致上表面的风压系数均大于1.0,最大值出现在雨篷靠近建筑侧的中心,然后往外呈减小趋势,最大值接近1.4,其原因是高层建筑阻挡引起气流下翻;2)下表面也呈正压,越靠近建筑风压系数越大,沿着水平线向外递减,最大值接近1.0,最小值约为0.6;3)上下表面叠加后,雨篷受到向下的正压,但数值上小于上表面,呈现“上压下压”的分布特征,在中间位置正压最大,最大值约为0.6.

图5 0°风向角平均风压系数Fig.5 Mean pressure coefficients under 0°azimuth
图6 给出了雨篷在60°风向角的风压系数,由图6 可知:1)雨篷上表面表现为正压,从迎风面向背风面递减,最大值约0.9,该分布主要由受到高层建筑的阻挡导致气流下翻引起;2)下表面迎风角区出现类似“锥形涡”的分布特征,迎风角区出现数值较小的负压,负压最大值约为-0.5;3)上下表面叠加后为正压,迎风角区出现较为明显的类似“锥形涡”的特征,且迎风面出现极值正压,最大值约达到1.2,超过上表面的最大值,其原因为迎风角区形成“上压下吸”的风压叠加情况.
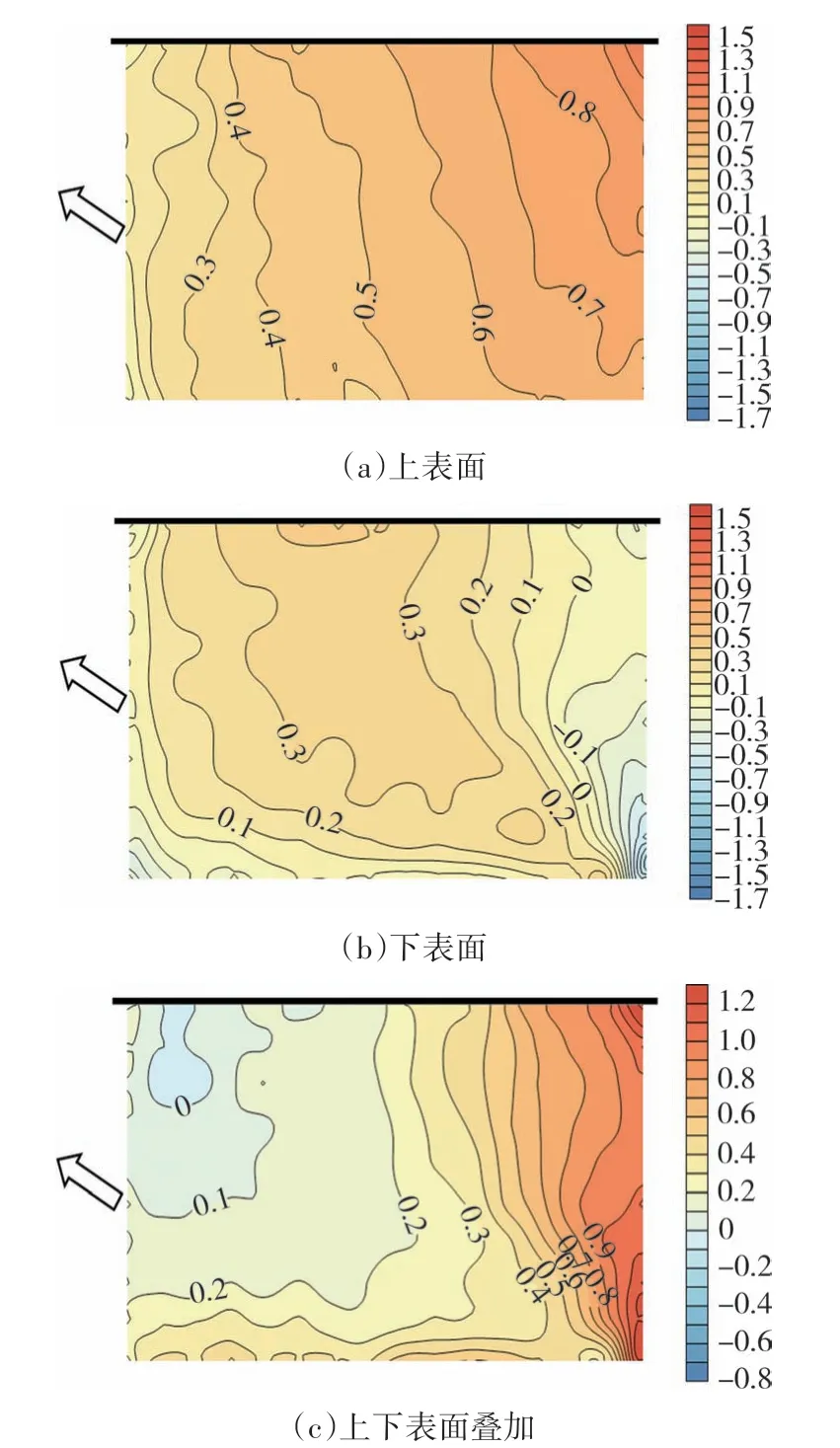
图6 60°风向角平均风压系数Fig.6 Mean pressure coefficients under 60°azimuth
图7 给出了雨篷在90°风向角的风压系数,由图7 可知:1)上、下表面均呈现负压;2)上表面的迎风区域出现柱状涡的特征,迎风面边缘的负压最大,沿着长度方向递减;3)下表面也呈柱状涡分布,但并不是很明显,其与下表面和地面距离较近相关;4)上下表面叠加后整体呈现负压特征,数值较小,说明上下表面的负压基本上相互抵消,呈现“上吸下吸”的分布特征,整体数值从来流前端向后端衰减.

图7 90°风向角平均风压系数Fig.7 Mean pressure coefficients under 90° azimuth
3 雨篷的整体升力系数
图8 给出了雨篷的整体升力系数,由图8 可知:1)上表面的整体升力系数在0°~90°风向角下变化剧烈.0°风向角下,升力系数出现负的最大值,数值为-1.24,原因在于上表面气流受到高层建筑的阻挡产生气流下翻;而90°风向角下,气流穿过雨篷表面,对上表面产生很大的吸力,升力系数出现正的最大值,数值为1.13;在100°~180°风向角下雨篷处于高层建筑的尾流区,受到的负风压基本不变,整体升力系数整体稳定在0.9左右.2)下表面的升力系数变化规律与上表面类似,但数值较小,主要是由于其与地面之间的距离较近引起的.0°风向角下升力系数出现负的最大值,数值为-0.76;90°风向角下升力系数出现正的最大值,数值为1.01;100°~180°风向角下的升力系数约为-0.7.3)由于上下表面的升力系数分布比较接近,因此叠加后呈相互抵消趋势,导致叠加后的升力系数较小,最大负值出现在0°风向角,数值为-0.48,在90°~180°数值几乎为零.

图8 各风向角下雨篷的整体升力系数Fig.8 Total lift coefficient under all azimuths
4 雨篷上下表面测点的相关性
各测点在各风向角下上下表面对应测点的相关系数γ如图9 所示,图中N为测点编号.相关系数γ绝对值大于0.5 为强相关,γ绝对值小于0.2 为弱相关.可以发现:1)雨篷上下表面测点仅在50°~70°风向角呈现较强的负相关特征,其他风向角均表现为正相关,对脉动风荷载,根据公式(6),上下表面负相关会使得叠加后的脉动风荷载变大[2];2)在50°~70°风向角下,雨篷迎风区域固支端与自由端上的测点呈现较强的负相关特征,而在雨篷中部的负相关特征较弱;3)对于同一排测点(如编号1~16),负相关较大值均出现在来流分离较为严重的迎风边,例如16号、32号或160号测点.

图9 各风向角下雨篷上下表面的相关系数Fig.9 Correlation coefficient of upper and lower surface under all azimuths
为探究雨篷表面相关性的具体分布情况,绘制典型风向角0°、60°、90°下相关系数图,如图10所示.由图10可知:1)0°风向角下,雨篷的上下表面测点整体呈现出正相关关系,雨篷中部的互相关系数较低,总体在+0.5 以下;2)在50°~70°的斜向角度风作用下,出现对结构不利的负相关系数,且数值较高,以60°为例,雨篷上下表面相关性在迎风角区出现数值较大的负相关区域,数值超过-0.5,为强负相关,导致叠加后的风压脉动值变大;3)90°风向角下,雨篷上下表面测点呈现出正相关关系,迎风区出现区域较小的弱相关区域,在远端互相关系数较高,呈现较强的相关性.
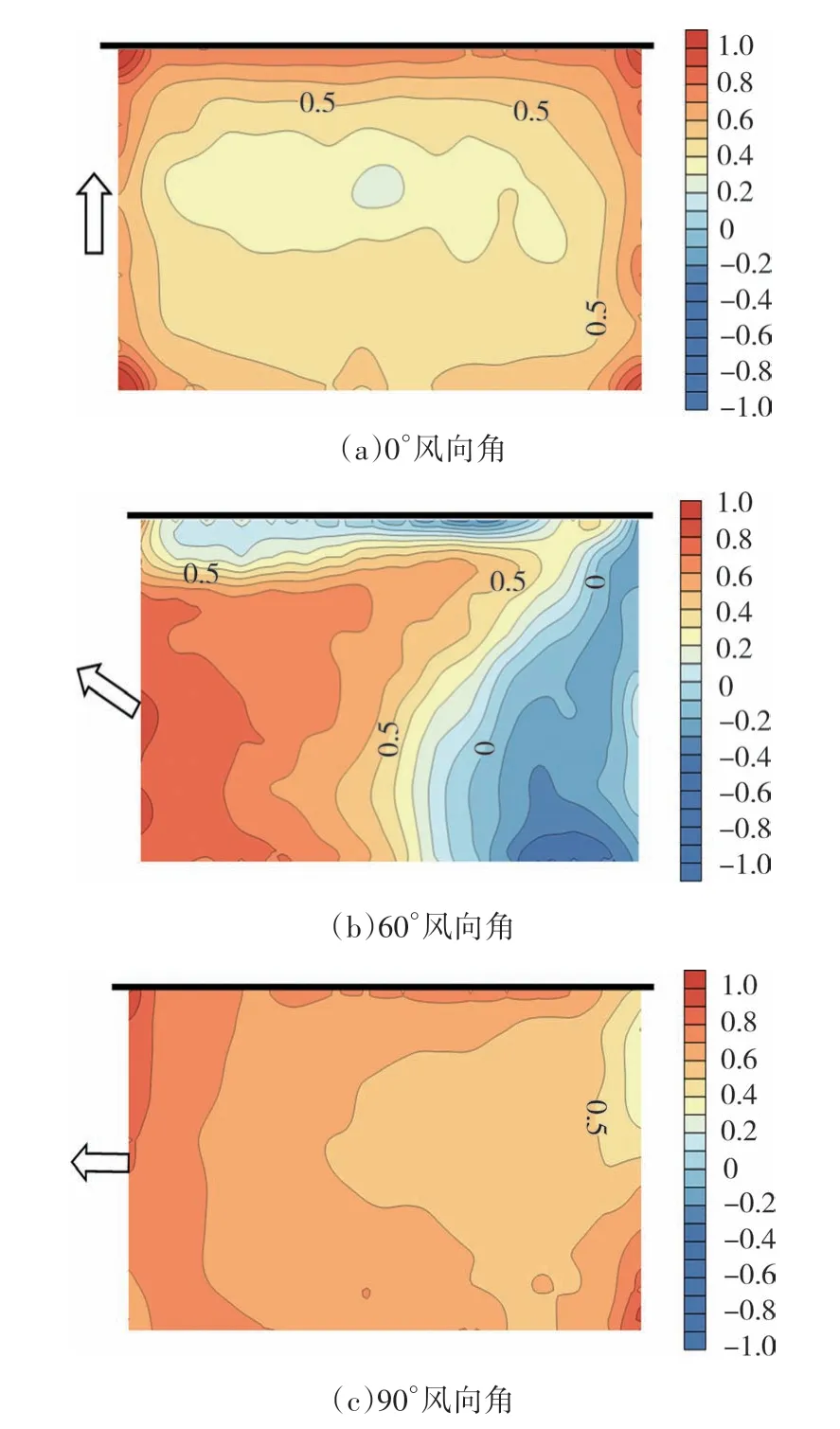
图10 典型风向角雨篷上下表面的相关系数Fig.10 Correlation coefficient of upper and lower surface under typical azimuths
5 测点和升力时程的非高斯特征
峰值因子法计算脉动风荷载需假定风荷载服从高斯分布,该方法对于屋盖结构中风压由特征湍流控制的区域不一定适用[15].非高斯分布的判断采用风压的三阶中心距SK(偏度)与四阶中心矩KU(峰度),确定划分非高斯区域[16-17]的标准为:|SK|>0.5 且|KU-3|>0.5.图11 给出0°、30°、60°和90°所有测点的偏度与峰度,从图11 中可以看出:叠加表面的峰度、偏度分布与单个表面有较大差异,叠加后的测点非高斯性比单个表面强.

图11 基准雨篷各点风压的偏度、峰度Fig.11 Skewness and kurtosis of wind pressures of base case
雨篷在0°和90°风向角下表面测点的非高斯性如图12和图13所示.由图可知:1)0°风向雨篷上、下表面整体呈现出较强的高斯特征,只在迎风区与尾流区出现零星的非高斯性测点,上下表面叠加后非高斯性测点数目增多,在表面的迎风区以及后方尾流区域出现数目较多的非高斯性测点;2)90°风向雨篷上表面测点几乎均为非高斯性,下表面测点除迎风区后方出现部分高斯性测点外,均呈现出非高斯特征,上下表面叠加后除了角部的2 个测点外,其他均为非高斯性测点.

图12 0°风向角各点风压的高斯和非高斯性Fig.12 Gaussian and non-Gaussian evaluation of pressure under 0° azimuth
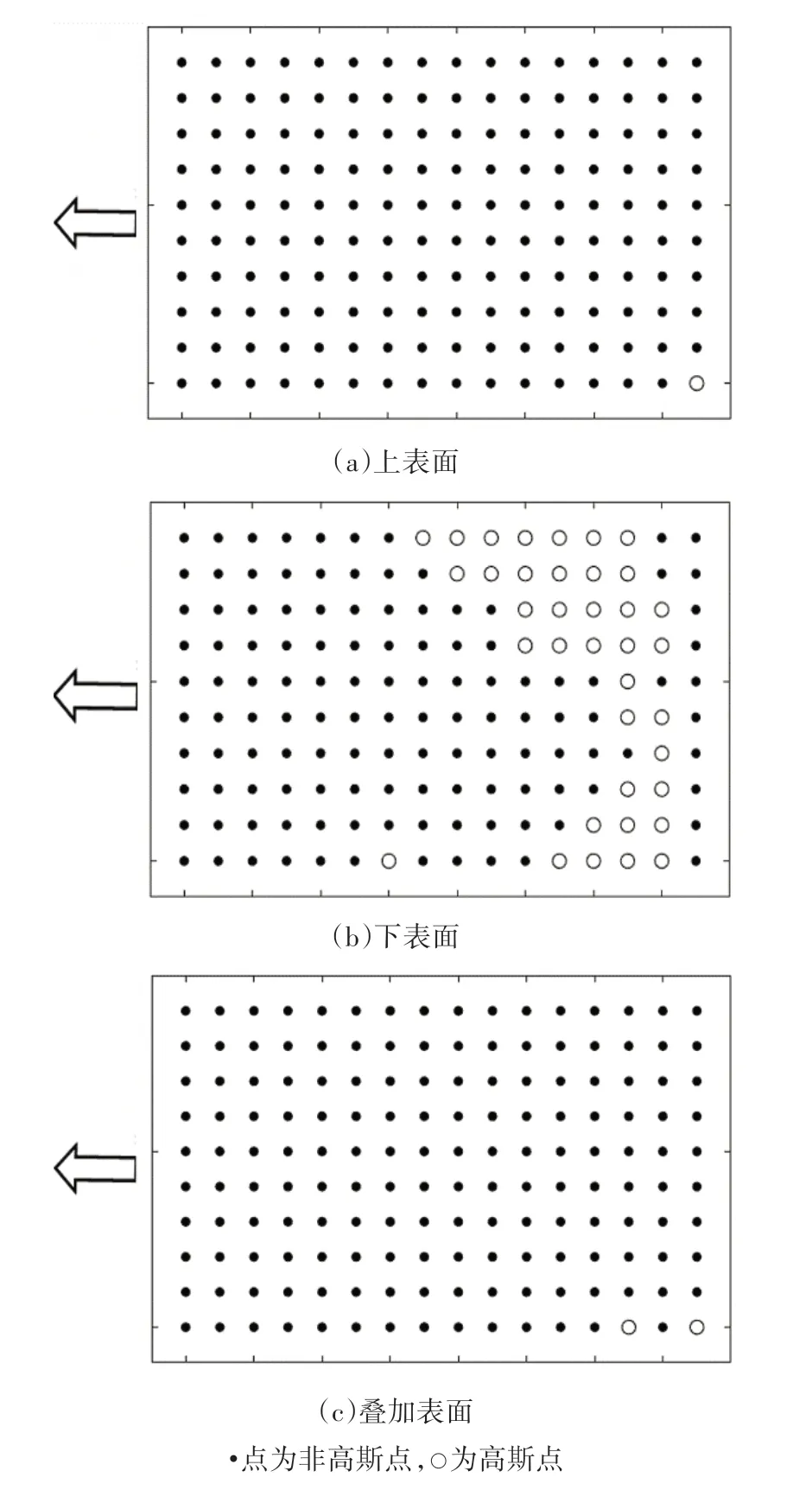
图13 90°风向角各点风压的高斯和非高斯性Fig.13 Gaussian and non-Gaussian evaluation of pressure under 90° azimuth
图14 给出了雨篷各风向角下升力系数时程的峰度值与偏度值,由图14 可知:1)上、下表面以及叠加表面在0°~70°风向时,升力系数的偏度与峰度呈现出高斯特征;2)从80°风向开始,升力系数的偏度值与峰度值开始出现明显的偏离,上表面、下表面以及上下表面叠加的升力系数均呈现出较强的非高斯特征,且均为大偏斜(SK>0.5)和高峰态情况(KU>3.5);3)上表面在110°~180°时,其非高斯特征远强于下表面,在160°风向达到极值,此时KU为14.5,SK为2.3;4)下表面升力系数的非高斯特征也较强,极值出现在160°风向,此时KU为8.7,SK为1.6;5)上下表面叠加工况在110°与170°风向时出现两个较为明显的极值,110°时KU为9.1、SK为1.6,170°时KU为14.2、SK为1.6.

图14 雨篷升力系数的偏度和峰度Fig.14 Skewness and kurtosis of total lift coefficient of canopy
6 全风向风压系数极值
由于雨篷表面风压的非高斯特征明显,使用BLUE算法[18]获得极值风压系数:将风压系数时程进行等长度分段,取每个分段时程的最大值、最小值,分别组成升序序列,降序序列,则极值按照下式计算:
式中:aj和bj为加权系数,N=10时,按表1取值.
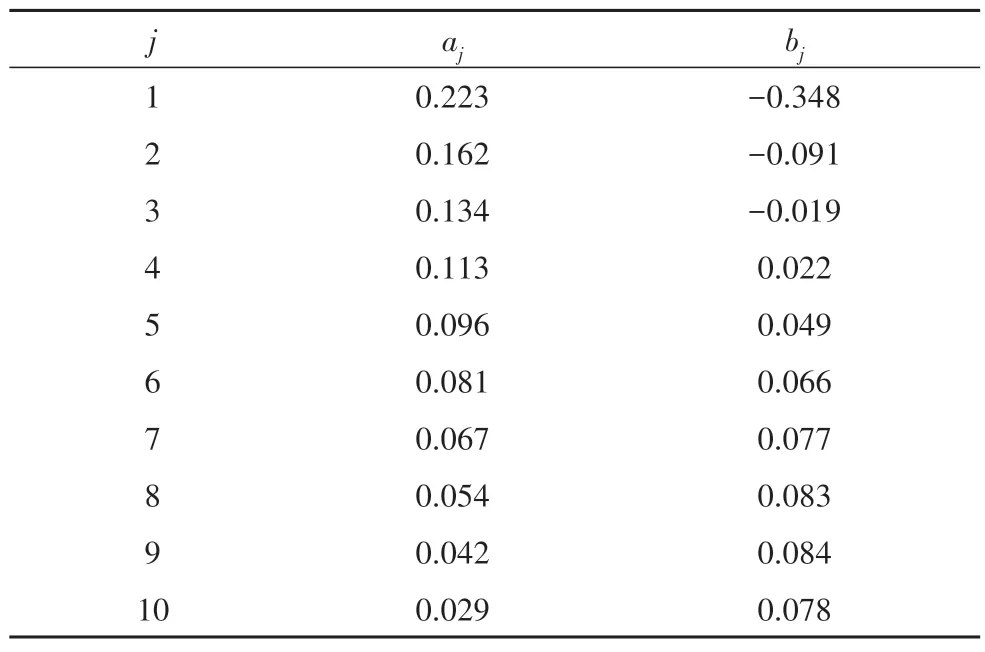
表1 加权系数取值Tab.1 Values of weighted coefficient
图15 和图16 给出了雨篷全风向风压系数极值正、负压的云图,由图15 和图16 可知:1)对于正压,上表面的极值正压大于下表面,其原因是上表面高层建筑阻挡引起气流下翻导致[19];靠近高层建筑侧的正风压大于靠近自由端侧,说明高层建筑的阻挡使得正风压增大;上下表面叠加后,雨篷的两个侧边的正风压大于中间位置.2)对于负压,上表面、下表面以及上下表面叠加的负风压绝对值均大于正风压;上表面的极值负风压绝对值大于下表面和上下表面叠加的结果;左右两侧的负风压较大.

图15 雨篷的正全风向极值风压系数Fig.15 Positive peak wind pressure coefficients of canopy under all azimuths

图16 雨篷的负全风向极值风压系数Fig.16 Negative peak wind pressure coefficients of canopy under all azimuths
全风向极值风压系数Cpe如表2 所示,考虑到雨篷通常按一个值设计,因此给出了所有位置的最大值,同时表中给出不同出挑长度D的结果.由表2 可知:1)上下表面叠加后的全风向极值负风压系数显著小于上表面和下表面,极值正风压系数略大于上表面和下表面;2)极值负风压系数的绝对值大于极值正风压系数;3)随着雨篷长度的增加,雨篷表面极值风压系数增大,且负风压系数增大较为明显.表1部分内容已被《建筑外围护结构抗风设计标准》(T/CECS 1048―2022)[20]采用.需要说明的是,荷载规范中采用阵风系数方法考虑围护结构设计风荷载,主要是考虑风的来流湍流,而本文方法同时考虑了风洞来流湍流和结构的特征湍流,结果更加直观.

表2 高层建筑外附雨篷极值风压系数Tab.2 Peak wind pressure coefficients of canopy affiliated to high-rise building
7 倾角和出挑长度对雨篷升力的影响
图17 给出了不同倾角高层建筑外附雨篷的升力系数随风向角的变化,由图17 可得:1)不同倾角下整体升力系数变化规律一致,均在0°风向角达到负极值,90°达到正极值;2)雨篷倾角按-10°、0°、10°变化时,0°至90°风向,整体升力系数依次递增,130°至180°,整体升力系数依次递减,但总体变化幅度较小[21].

图17 不同倾角整体升力系数对比(D=12 m)Fig.17 Comparison of total lift coefficient of different attack angles(D=12 m)
图18 给出了不同出挑长度雨篷的升力系数随风向角的变化,由图18 可得:1)不同出挑长度雨篷整体升力系数变化规律近似,除D=4 m 工况在30°风向达到负极值外,其余工况均在0°风向角达到负极值,90°达到正极值;2)随出挑长度的变化,整体升力系数变化无规律,原因在于下部气流较为紊乱[22],在50°~90°风向角下,气流通畅,整体升力系数随出挑长度的增大而减小.

图18 不同出挑长度时的整体升力系数(α=0°)Fig.18 Total lift coefficient of different cantilevered length(α=0°)
8 结论
1)高层建筑外附雨篷在正迎风情况下上表面的风压系数均大于1.0,最大值接近1.4,其原因是气流受到后方高层建筑的阻挡下翻;雨篷下表面也呈正压,最大值接近1.0;雨篷上、下表面在侧风情况下均呈现负压,上下表面叠加后整体呈现负压特征,数值较小,呈现“上吸下吸”相互抵消的分布特征.
2)高层建筑外附雨篷上表面的整体升力系数在正迎风工况出现向下的最大压力,最值为-1.24,在侧风工况出现向上的最大吸力,最值为1.13;下表面升力系数也在正迎风和侧风工况出现最大压力和吸力,最值分别为0.76 和1.01.上下表面叠加后升力系数较小,系上下表面风压相互抵消所致.
3)高层建筑外附雨篷上下表面对应测点的互相关系数在迎风区较低,在远端较高,且在50°~70°风向下迎风边呈现较强的负相关;雨篷上表面的极值正压大于下表面,其原因是高层建筑阻挡引起气流下翻.
4)上下表面叠加后测点风压的非高斯性相较上表面、下表面均增强;上、下表面风压在侧风工况下非高斯特征明显,原因为气流在该风向下发生显著的涡脱;上、下表面以及上下表面叠加后的升力系数,0°~70°时其偏度值与峰度值均较小,呈现高斯分布特征,80°~180°时呈现出较强的非高斯分布特征.
5)高层建筑外附雨篷倾角按-10°、0°、10°变化时,整体升力系数随着倾角增大而递增,但变化幅度较小;整体升力系数随出挑长度的变化较小,在50°~90°风向角下整体升力系数与随出挑长度的增大而减小.

