基于三参数破坏准则的均质边坡稳定性上限分析
赵炼恒 ,赵伟龙 ,韦彬 ,贾光龙 ,胡世红 †
[1.中南大学 土木工程学院,湖南 长沙 410075;2.轨道交通工程结构防灾减灾湖南省重点实验室(中南大学),湖南 长沙 410075;3.重载铁路工程结构教育部重点实验室(中南大学),湖南 长沙 410075;4.深圳市综合交通与市政工程设计研究总院有限公司,广东 深圳 518003]
边坡稳定性一直以来是岩土工程中的热点话题.目前分析边坡稳定性的方法主要有极限平衡法[1-2]、有限元法[2-3]和极限分析法[4-7]等.由于极限分析法具有清晰的物理意义以及能得到严格的求解范围[8],近年来在边坡稳定性问题上获得了广泛的应用[4-10].贺志军等[4]基于极限分析上限定理和蒙特卡l罗法,在非线性Mohr-Coulomb 破坏准则下进行了边坡可靠度分析.王智德等[5]利用极限分析上限法和体积力增量法,考虑含多岩层错动的结构面的块体模型,推导出计算边坡稳定系数的公式,并与离散元模拟结果对比验证其方法的有效性.Tang 等[6]利用非线性序列二次规划法优化了边坡安全系数的目标函数,并基于极限分析上限定理和强度折减法,考虑堆载、孔隙水压力和水平地震力等因素的影响,绘制了各向同性均质边坡的稳定性图表.在极限分析中,边坡失稳的机制以旋转破坏和平移破坏为主[11],经验表明[11-12],在评价边坡稳定性时旋转破坏比平移破坏产生了更好的界限.对于旋转破坏机制,绝大多数研究[9,13-14]均假定边坡的破坏面为对数螺旋线.但已有研究显示[15],服从线性Mohr-Coulomb 破坏准则的边坡发生旋转破坏时,其潜在滑动面是对数螺旋线;而在非线性准则下,边坡潜在滑动面并非单一对数螺旋线,当研究中不能真实地体现岩土体的力学特性,就会使结果与真实状况存在一定的差异.此外,经典的极限分析理论大多基于线性Mohr-Coulomb破坏准则进行研究,然而大量的试验表明岩土体的强度包络线具有显著的非线性特征[16-17].因此,为了较为准确地评价边坡稳定性,许多学者基于非线性破坏准则对边坡稳定性进行了大量研究.Yang 等[18]利用“外切线技术”将非线性破坏准则转化为线性Mohr-Coulomb 破坏准则,获得了非线性破坏准则下的单一抗剪强度指标,进而结合塑性上限定理得到了边坡的稳定性系数.Li 等[19]基于Hoek-Brown 破坏准则和极限分析有限元上、下限技术,采用拟静力法分析了边坡在水平地震荷载作用下的稳定性,通过与极限平衡法的结果进行对比,说明了对于陡立边坡,极限平衡法得到的稳定系数偏小.Zhao等[20]基于三种抗剪强度折减策略分别计算非线性破坏准则下均质边坡的安全系数.Zuo等[21]为了确定滑坡滑动面的抗剪强度参数,提出了一种基于非线性Mohr-Coulomb 破坏准则的可靠性反分析方法,并用工程案例验证了此方法的可行性.可以看出,基于非线性破坏准则的边坡稳定性问题在分析过程中通常会将非线性破坏准则转化为线性Mohr-Coulomb 准则来研究[4,7,10],即潜在滑动面上的岩土体采用相同的抗剪强度参数,无法真实地反映出抗剪强度参数随应力状态变化的非线性特征,因此本质上依旧属于线性破坏准则分析.然而对于Baker[22]提出的三参数非线性破坏准则的边坡稳定性研究鲜有报道,该三参数非线性破坏准则是一种广义岩土体破坏准则,常规Mohr-Coulomb 破坏准则、Griffith 破坏准则以及Hoek-Brown 破坏准则均为其特例.因此,开展三参数非线性破坏准则的边坡稳定性分析研究对于拓展该破坏准则在岩土工程中的应用以及丰富边坡稳定性分析理论具有重要的研究意义.
尽管在现有的极限分析有限元方法中已经实现了Hoek-Brown 破坏准则在岩土工程问题中的应用[23-25],但对于非线性Mohr-Coulomb 破坏准则以及三参数破坏准则尚存在难点,主要是由于这两种破坏准则的主应力表达式较为复杂,且在应力空间中屈服面存在不连续点,这给数值计算方法带来了巨大的挑战.因此,本文基于极限分析上限定理,假定均质边坡在极限状态下发生旋转破坏,采用拟静力方法考虑地震荷载作用,基于力学平衡方程建立临界滑动面的泛函表达式,进一步采用变分原理获得了临界滑动面及其应力分布的微分方程组;通过四阶Runge-Kutta 方法结合变分横截条件、边界条件求解临界滑动面及其上应力;最后根据虚功原理,采用智能免疫算法得到边坡的最小临界高度.通过与极限分析有限元方法进行对比,验证了本文方法在非线性破坏准则条件下进行边坡稳定性评估的有效性与准确性.在此基础上,分析了非线性强度参数、边坡倾角、水平地震加速度系数等对边坡稳定系数和潜在滑动面及其应力分布的影响规律.
1 三参数非线性破坏准则
Baker[22,26]通过大量试验提出了一种描述岩土体非线性的破坏准则,证明大部分岩土体材料均遵循如下三参数非线性破坏准则(见图1):
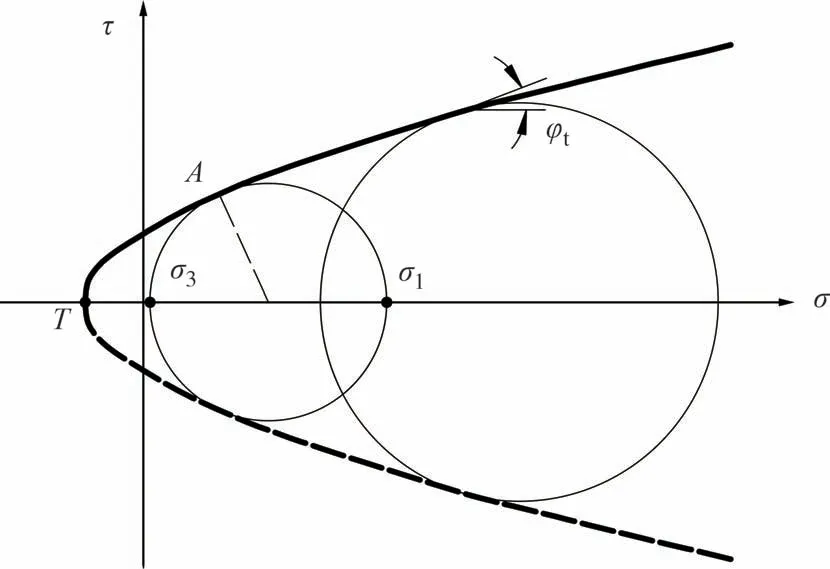
图1 非线性强度包络线Fig.1 Nonlinear strength envelope
式中:τ为切向应力;σ为法向应力;Pa为大气压强,大小为100 kPa;A为比例参数,控制剪切强度大小;T为转换参数,控制包络线与σ轴交点位置;n为无量纲参数,控制包络线曲率.
图1中:σ1、σ3分别为最大和最小主应力,并规定以压应力为正;φt为瞬时抗剪强度参数指标.
Baker[26]给出了各参数的取值范围:0 在极限状态下,假设均质边坡的潜在滑动面y(x)[极坐标系下为r(θ)]通过坡脚,坡面函数为y1(x),α和β为边坡倾角.边坡坡顶破坏点(即滑入点)至坡脚的垂直高度为H,水平距离为L;坡顶点与坡脚的垂直高度为H1,水平距离为L2;坡顶点与滑入点的距离为L1,建立如图2所示的均质边坡旋转破坏机制.滑动面以上岩土体可视为刚性体,以角速度沿滑动面绕点O转动,且边坡失稳时瞬时变形忽略不计.假定均质边坡岩土体材料服从三参数非线性破坏准则和相关联流动法则,根据极限分析上限定理,塑性速度矢量δw与滑动面的夹角为φt. 图2 均质边坡旋转破坏机制Fig.2 Rotational failure mechanism of homogeneous slope 非线性破坏准则下,滑动面上单位面积的内能耗散功率为[8,27]: 将式(3)代入式(2)并积分可得临界状态下滑动面上总的内能耗散功率 式中:r表示滑动面上一点的旋转半径;θ为极径与水平方向的夹角,顺时针为正. 在本文中,外力包含重力和地震力,此处采用水平和垂直地震加速度系数kx、ky表征地震对边坡稳定性的影响,由于都是体积力,因此可一并计算.值得注意的是,当kx=0、ky=1.0 时与自然条件下相同,即只有重力作用.基于图2 的边坡滑动破坏机制,在体积力作用下,外力功率可计算如下 式中:We为滑动体外力功率;W为坐标轴x、x=xn与滑动面所围区域的外力功率;WⅠ为区域Ⅰ的外力功率;WⅡ为区域Ⅱ的外力功率;WⅢ为区域Ⅲ的外力功率. 式中:γ为岩土体材料容重,单位kN/m3. 根据虚功率原理,有 将式(6)代入式(7)中并整理可得 在极限状态下,滑动体的力学平衡条件和材料屈服条件必须同时满足,且认为当能量平衡和力学平衡条件同时满足时可以获得最小的上限解答[15].因此,在地震拟静力荷载和自重作用下,滑动体的力学平衡方程如下 式中:Q、V分别为滑动体水平和竖直方向的合力;M为滑动体对坡顶滑入点的矩. 因此,滑动体的总虚功可表示为 式中:δu、δv和δΩ分别为水平、竖直和转动的虚位移. 将式(10)代入式(11)可得总虚功为: 当I的一阶变分为零时,边坡处于临界状态.此时,泛函I满足如下欧拉方程: 式中:G表示临界状态下边坡潜在滑动面上正应力和切应力满足的相关关系,在本文中即为三参数破坏准则. 对于Baker提出的三参数非线性屈服准则,有: 于是将式(15)(22)代入式(21)可得: 由式(23)可知,线性准则下,即φt为常量时,均质边坡潜在滑移面为对数螺旋线;反之,在非线性准则下,边坡潜在滑移面并非单一对数螺旋线. 同理,将式(16)(18)代入式(17c)中可得: 通过变分原理的欧拉方程,得到了滑动面及其正应力分布的一阶微分方程组,求解该常微分方程组,还需要边界条件.由变分极值原理可知,当极值曲线的端点不固定时,泛函取极值的必要条件为满足变分横截条件[28].由于坡顶破坏点在坡顶表面上移动,因此,泛函取极值的变分横截条件为: 需要注意的是,在滑动面端点处,有: 故含有kx和ky的两项消失,再结合式(15)和(22)可得: 由于滑动体的瞬时变形忽略不计,可采用变形前的尺寸进行分析.因此,根据图2 的几何关系,有以下等式成立: 根据2.1节能耗分析,可以获得边坡给定参数条件下的临界高度,求解流程如图3 所示.详细计算步骤如下: 图3 边坡临界高度求解流程图Fig.3 Flow chart for solving critical height of slope 1)已知边坡坡顶倾角及坡面倾角、岩土体强度参数和地震系数; 2)假定一组输入参数(r0,θ0),根据变分横截条件[(式(30)]求解坡顶破坏点处的正应力σ0; 3)选择迭代步长Δθ,使得θi+1=θi+Δθ,根据Runge-Kutta 法在区间[θi,θi+1]上求解式(23)和式(26),得到滑动面上点(i+1)的坐标(ri+1,θi+1)和应力值σi+1、τi+1; 4)计算点(i+1)处累计的内能耗散功率和外力功率,再根据虚功率平衡原理,求解式(8)得到坡顶破坏长度L1; 5)若L1大于零,则根据式(31)计算相应的边坡坡度和高度,反之则返回第3步; 6)判断计算边坡坡度是否和已知边坡坡度相等,若不相等,则返回第2步; 7)输出(r0,θ0,H),得到均质边坡临界高度最优上限解及其对应的潜在滑动面. 其中,通过第2 步~第6 步可以得到已知坡度下边坡的临界高度,进而利用二维免疫算法得到最优上限解.需要说明的是,由于本文构建的边坡潜在滑动面通过坡脚,因此上述推导公式只适用于坡脚破坏机制,对于坡面及坡脚以下这两类破坏机制,该程序尚不能获得其临界高度. 免疫算法是一种受生物免疫系统的启示而形成的智能搜索算法.此算法适用于求解连续函数的极值问题,对于非连续函数的极值问题,也具有很强的全局搜索能力.基本原理是将优化问题中待优化的问题、可行解、可行解质量与免疫系统中抗原、抗体、免疫细胞与抗原的亲和度一一对应.因此可以将生物免疫应答中的进化过程转换成数学上的寻优过程,免疫算法采用群体搜索策略,通过迭代计算,最终以较大的概率得到问题的最优解.主要步骤如下. 1)假定免疫个体维数为D1,免疫个体数目为N,则初始种群的位置表示为: 式中:rand(0,1)表示在[0,1]上服从均匀分布的随机数;xij(0)表示初代种群中第j个粒子的第i个分量的位置. 2)计算个体的亲和度、抗体浓度以及激励度,并按激励度大小进行排序. 式中:J表示激励度;U为该个体的亲和度值,即函数值;K为抗体浓度;p、q称为激励度系数. 3)取激励度前N/2 个个体进行免疫操作(克隆、变异和克隆抑制),免疫后的种群重新计算激励度. 4)随机生成N/2个个体的新种群,计算个体的亲和度、抗体浓度以及激励度;免疫种群与随机种群合并,按激励度大小排序,进行免疫迭代. 5)反复执行步骤2)~4),直至达到最大免疫迭代次数或所要求的收敛精度结束. 为了验证本文非线性上限变分分析结果的准确性和有效性,将本文方法与极限分析有限元方法(OPTUM G2 2021)计算结果进行对比.对比分析中采用非线性Hoek‒Brown 准则,由于OPTUM G2 中的Hoek-Brown 破坏准则是由地质参数D、σci、GSI 和mi表示,因此在对比验证之前应进行参数的转换.Hu等[29]提出了一种将Hoek‒Brown 参数与非线性Mohr‒Coulomb破坏准则强度参数的转换计算方法.由于非线性Mohr‒Coulomb 准则与本文的三参数破坏准则表达形式一致,故也可采用此方法得到Hoek‒Brown准则参数与三参数破坏准则参数之间的转换关系,详细步骤如下. Hoek 等[30]提出了一种方法实现两种形式的Hoek‒Brown 破坏准则之间的参数转换.Hoek-Brown破坏准则的主应力形式为: 式中:σ1和σ3分别为最大和最小主应力;a、mb和s是与D、σci、GSI 和mi相关的无量纲参数,D为扰动因子,σci为单轴抗压强度,GSI为地质强度参数,mi为材料常数[31]. 此外,以切向应力和法向应力表示的Hoek-Brown破坏准则为: 式中:τ和σ分别为切向和法向应力;A2和B2为反映材料特性的无量纲参数;σtm为单轴抗拉强度. 当给定参数D、σci、GSI和mi时,可以通过线性回归分析得到参数A2、B2和.另外,对比式(1)和式(37)可知,切应力形式的Hoek-Brown 破坏准则与三参数破坏准则表达式一致,故可以获得参数(A2、B2、σci和σtm)和(n、T和A)之间的转换关系,具体关系如下: 算例边坡的形状尺寸和材料参数均取自孙超伟等[32]的研究,具体参数为:H=10 m,α=0°,β=45°,γ=25 kN/m3,kx=0,ky=1.0,弹性模量E=5 000 MPa,泊松比μ=0.3,σci=25 MPa,mi=2,GSI=5,D=0. 采用OPTUM G2 建立边坡模型,土体材料服从Hoek-Brown 破坏准则和相关联流动法则,模型设置标准边界条件,即左右边界设置法向约束、底部边界设置固定约束.结合强度折减和网格自适应技术,采用三节点三角形单元,单元数量为3 000个. 由OPTUM G2 的有限元极限分析法(FELA)强度折减分析,可以获得均质边坡的安全系数、剪切耗散带以及滑动带上的主应力分布,一般情况下可认为该剪切耗散带即为边坡的潜在滑动面.此外,通过本文方法亦可获得边坡的安全系数、临界状态下的潜在滑动面及其正应力和切应力分布,由式(39)可将该正应力和切应力转化为主应力,从而与极限分析上限有限元滑动带上的主应力结果进行对比,以此来验证本文方法的准确性和有效性,如图4所示. 图4 对比分析结果Fig.4 Comparative analysis results 图4(a)为计算滑动面与极限分析上限有限元剪切耗散带的对比.可以看出,两者形状基本吻合.本文方法计算的安全系数Fs=1.073,OPTUM G2 计算的安全系数Fs=1.125,相对误差为4.6%.由于切应力形式的Hoek‒Brown 准则与三参数破坏准则之间的参数转换遵循一一对等原则,因此相对误差的主要来源在于两种形式的Hoek‒Brown 破坏准则的参数转换. 图4(b)为两种方法计算所得滑动面上σ1和σ3的对比.不难看出,两者都是先增大后减小的变化趋势;两者出现极大值的位置基本一致,并且出现最大主应力的位置不在坡脚处.因此,以上对比可以证明本研究的准确性和有效性,能够为边坡的加固设计提供理论支持和合理参考. 根据前述计算方法,求解了给定边坡的临界高度.为了方便研究,采用了Baker[33]定义的稳定系数Fn,计算公式如式(40): 式中:Fs为边坡安全系数,本文求解边坡临界高度,即Fs=1. 为探究岩土体非线性强度参数、地震荷载、边坡倾角等因素对边坡稳定性的影响规律,采用上述极限分析上限定理,计算边坡的临界高度,再由式(40)计算边坡的稳定系数,以Fn为纵坐标绘制如图5 所示的影响规律曲线.各图例中非线性强度参数(T、A、n)、边坡倾角(β)及水平地震加速度系数(kx)的取值如表1所示,此外ky=1.0,γ=25 kN/m3,α=0°. 表1 不同图例下各参数取值Tab.1 Values of parameters in different legends 图5 不同参数对边坡稳定系数影响规律分析Fig.5 The influence of different parameters on slope stability coefficient 图5(a)研究了无量纲参数T从10~30 变化以及n从0.5~0.9 变化的条件下对稳定系数Fn的影响.计算结果表明:当无量纲参数T相同时,随着n的增大,边坡稳定系数逐渐减小,当n≥0.6 时,减小的趋势出现加快,且当T越大时,减小的趋势越显著;当n相同时,随着无量纲参数T的增大,边坡稳定系数逐渐增大,且当n越大时,增大的幅值越小. 图5(b)研究了无量纲参数A从1.0~3.0 变化以及n从0.5~0.9 变化的条件下对稳定系数Fn的影响.计算结果表明:当无量纲参数A相同时,稳定系数随n的增大呈减小的趋势,且这种趋势越来越缓慢;当n相同时,无量纲参数A对稳定系数几乎没有影响. 图5(c)研究了边坡倾角β从40°~80°变化以及n从0.5~0.9 变化的条件下对稳定系数Fn的影响.计算结果表明:当边坡倾角β相同时,随着n的增大,边坡稳定系数逐渐减小,当n≥0.8 时,减小的趋势出现明显地减缓,且当β越大时,减缓趋势越显著;当n相同时,稳定系数随边坡倾角β的增大而减小,且减小的趋势越来越缓慢. 图5(d)研究了地震系数kx从0.10~0.30 变化以及n从0.5~0.9 变化的条件下对稳定系数Fn的影响.计算结果表明:当地震系数kx相同时,稳定系数随n的增大而减小,当n≥0.6 时,减小的趋势出现明显地加快,且当kx越小时,减小的趋势越显著;当n相同时,随着kx的增大,边坡稳定系数逐渐减小,且当n越大时,减小的幅值越小. 计算边坡稳定系数是为了给边坡稳定性评估提供量化指标,但是当边坡稳定性不足时,则需要对其采取加固防护措施,而加固措施的选择取决于最危险滑动面位置.因此,确定边坡潜在滑动面位置显得尤为重要.本节研究了非线性强度参数、边坡倾角、地震系数等因素对潜在滑动面及其应力分布的影响规律. 由图6(a)可知,L1(坡顶点距坡顶破坏点的距离)随着无量纲参数T的增大而增大,H(坡顶破坏点至坡脚的垂直高度)随着T的增大同样增大;由图6(b)可知,坡顶破坏点(y=0 m 处)的正应力随着T的增大而减小,滑动面上的最大正应力随着T的增大而增大,且出现最大正应力的位置不在坡脚处. 图6 不同T时滑动面及其应力分布Fig.6 Sliding surface and its stress distribution with different T 由图7(a)可知,随着无量纲参数A的增大,L1逐渐增大,并且H随着A的增大同样增大;由图7(b)可知,坡顶破坏点的正应力为0,这是由于当T=0 时最小正应力为0,不存在负值,且根据边界条件式(30)计算也可以得到此结果,同时由图可知滑动面上的最大正应力随着A的增大而增大,且坡脚处出现正应力最大值. 图7 不同A时滑动面及其应力分布Fig.7 Sliding surfaces and its stress distribution with different A 由图8(a)可知,随着边坡倾角β的增大,L1逐渐减小,并且H随着β的增大同样减小;由图8(b)可知,滑动面上的最大正应力随着β的增大而减小,当β≤60°时,出现最大正应力的位置不在坡脚处. 图8 不同β时滑动面及其应力分布Fig.8 Sliding surface and its stress distribution with different β 由图9(a)可知,L1随着地震系数kx的增大而增大,但是H随着kx的增大而减小;由图9(b)可知,坡顶破坏点的正应力随着kx的增大而减小,并且滑动面上的最大正应力随着kx的增大同样减小,出现最大正应力的位置不在坡脚处. 图9 不同kx时滑动面及其应力分布Fig.9 Sliding surface and its stress distribution with different kx 基于三参数非线性破坏准则和极限分析上限定理,建立均质边坡旋转失稳机制,考虑地震荷载的作用,根据力学平衡方程结合变分原理推导了边坡潜在滑动面及其应力分布函数的微分方程组,采用Runge-Kutta 方法进行求解,并根据虚功率原理结合免疫算法求解了边坡的最小临界高度.本文无需假定边坡潜在滑动面形式,且避免采用“外切线技术”引入瞬时抗剪强度指标,保证了滑动面上抗剪强度参数与应力的非线性关系,可真实反映岩土体材料的非线性特征,并且适用于任何形式的非线性破坏准则,相较于目前嵌入非线性破坏准则尚不完善的极限分析有限元方法,本文方法在处理非线性破坏准则方面具有一定的优越性.该方法进一步分析了非线性强度参数、地震荷载、边坡倾角等因素对边坡稳定性的影响规律,主要结论如下: 1)非线性强度参数n和边坡倾角β对边坡稳定系数的影响显著,无量纲参数T和地震系数kx随着n的增大对稳定系数的影响越来越小,而无量纲参数A对稳定系数几乎没有影响. 2)L1随着无量纲参数T、A和地震系数kx的增大而增大,随着边坡倾角β的增大而减小;H随着T、A的增大而增大,随着β、kx的增大而减小. 3)潜在滑动面上最大正应力随着无量纲参数T、A增大而增大,随着边坡倾角β和地震系数kx增大而减小,与各参数影响边坡临界高度H的结果相似,并且当T=0时,坡顶破坏点(y=0 m处)正应力为0.2 上限分析
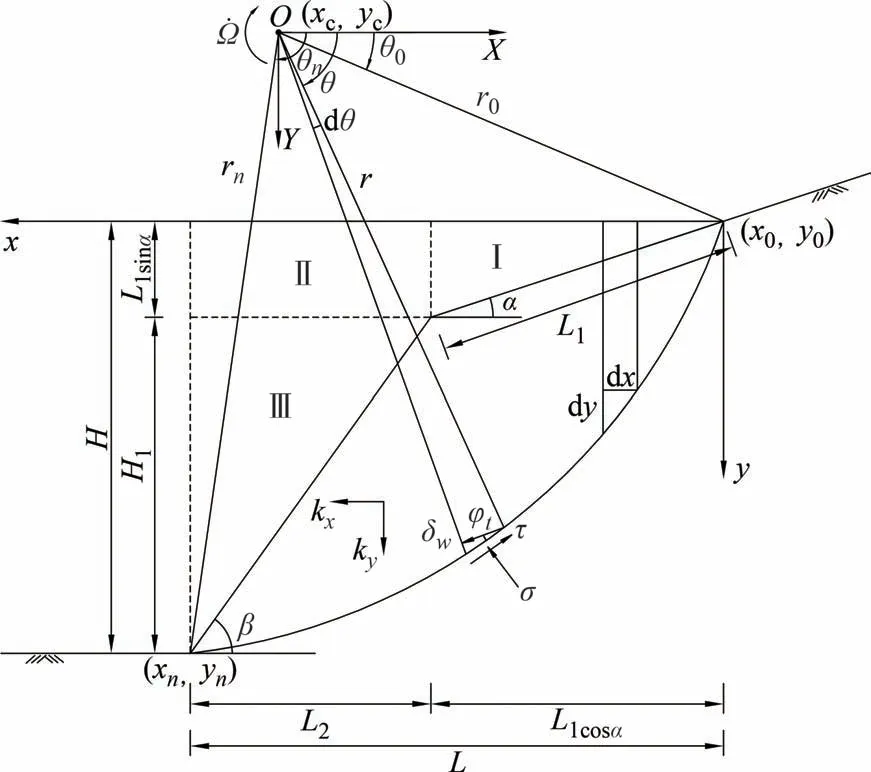
2.1 能耗分析
2.2 求解步骤
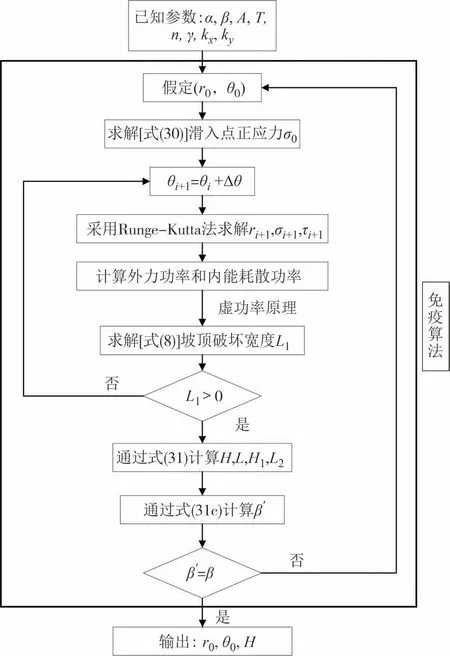
2.3 免疫算法
3 对比分析
3.1 参数转换
3.2 算例验证
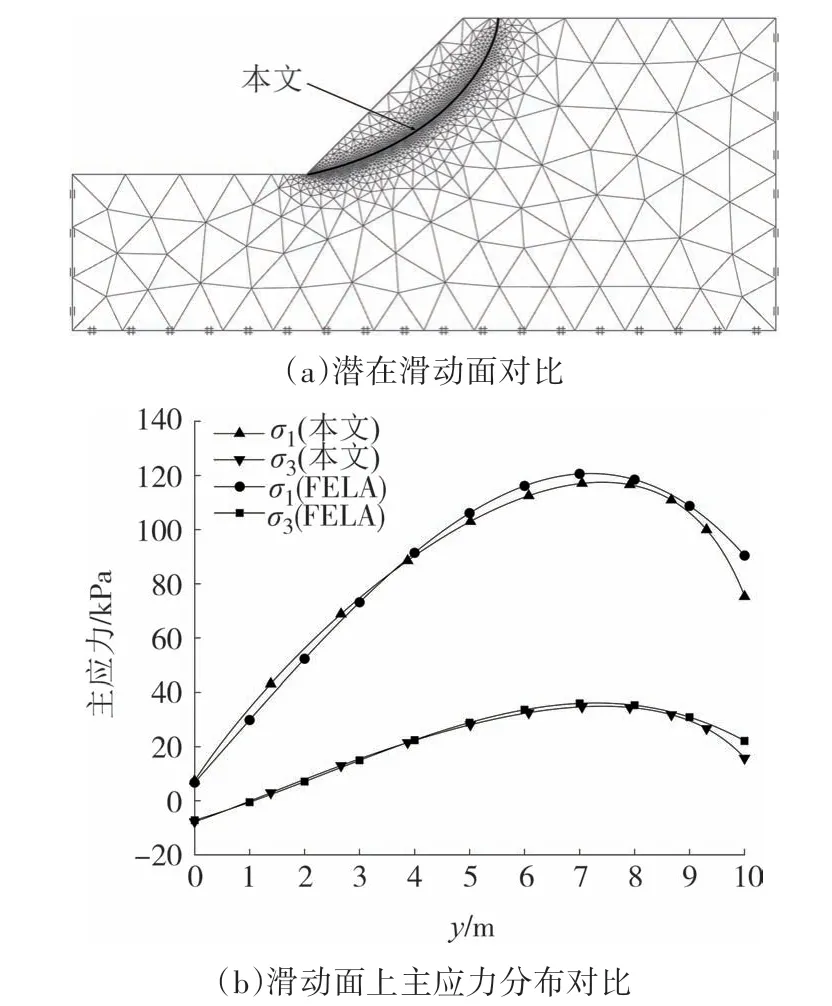
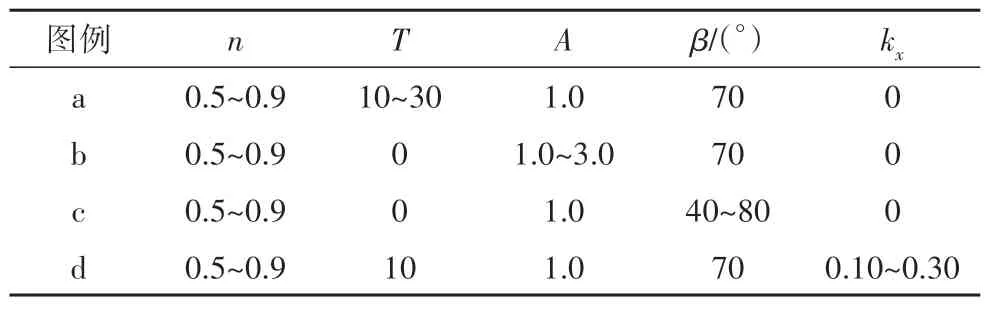
4 参数分析
4.1 稳定系数分析
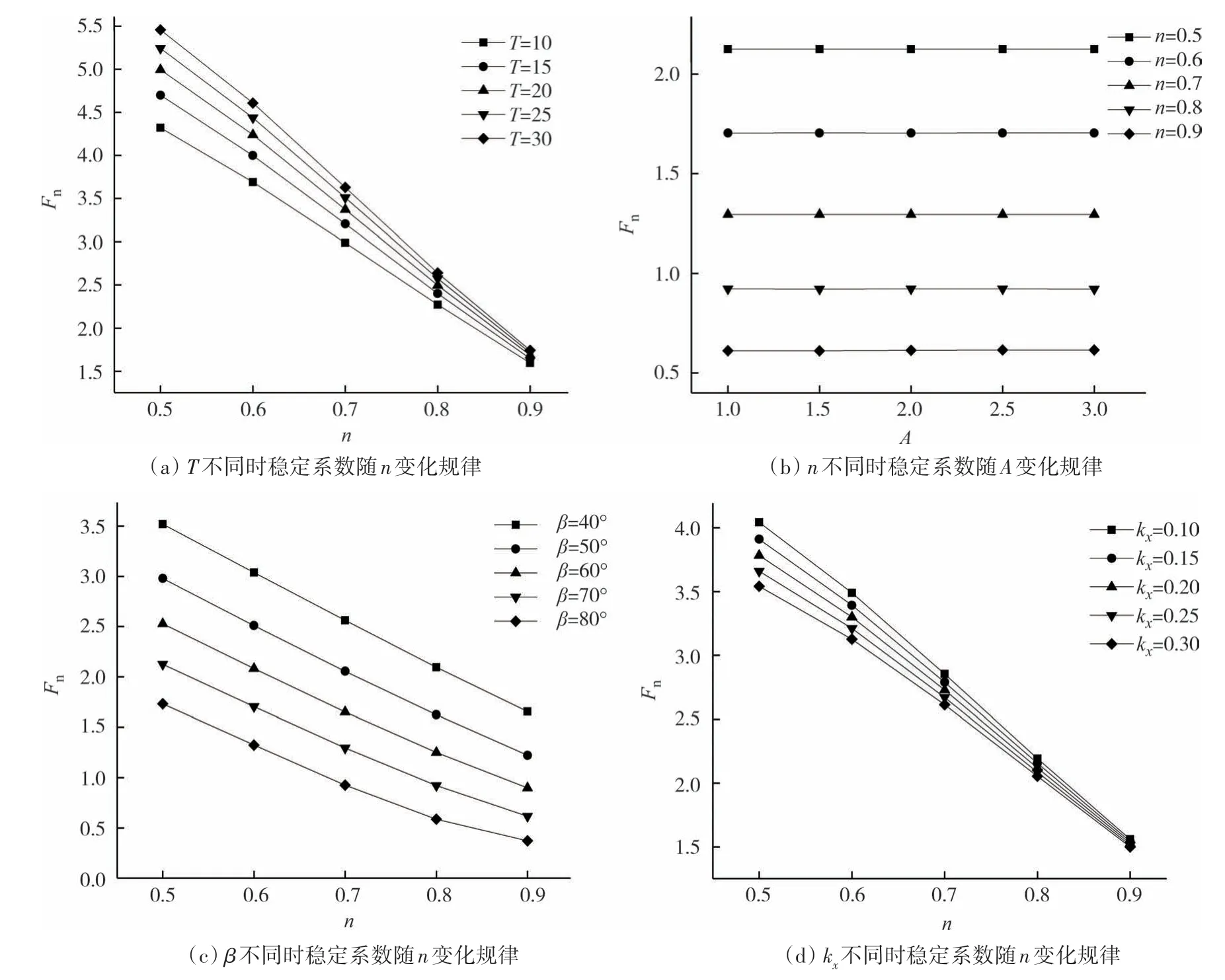
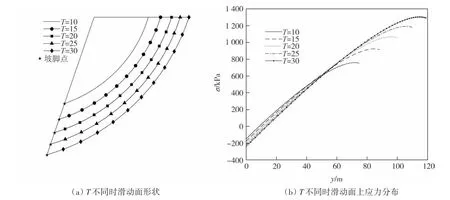
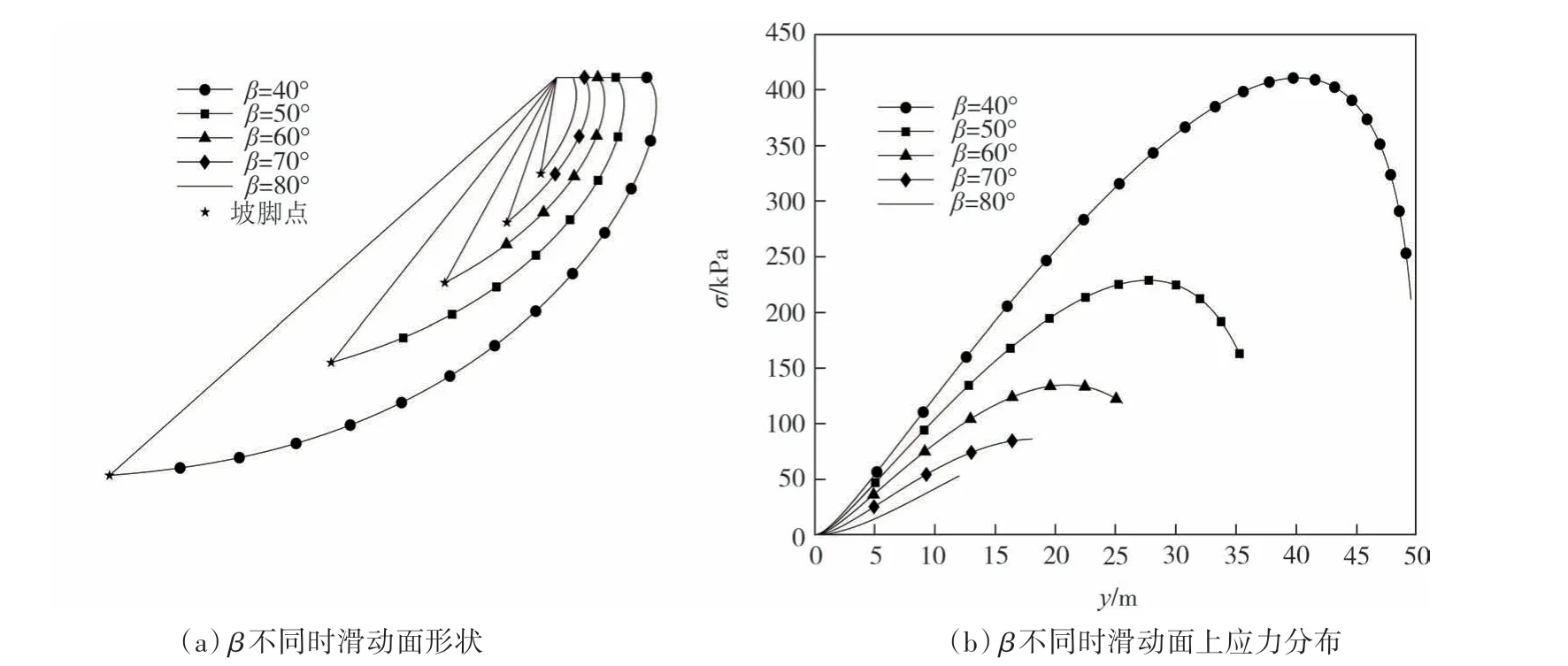
4.2 滑动面及其应力分析
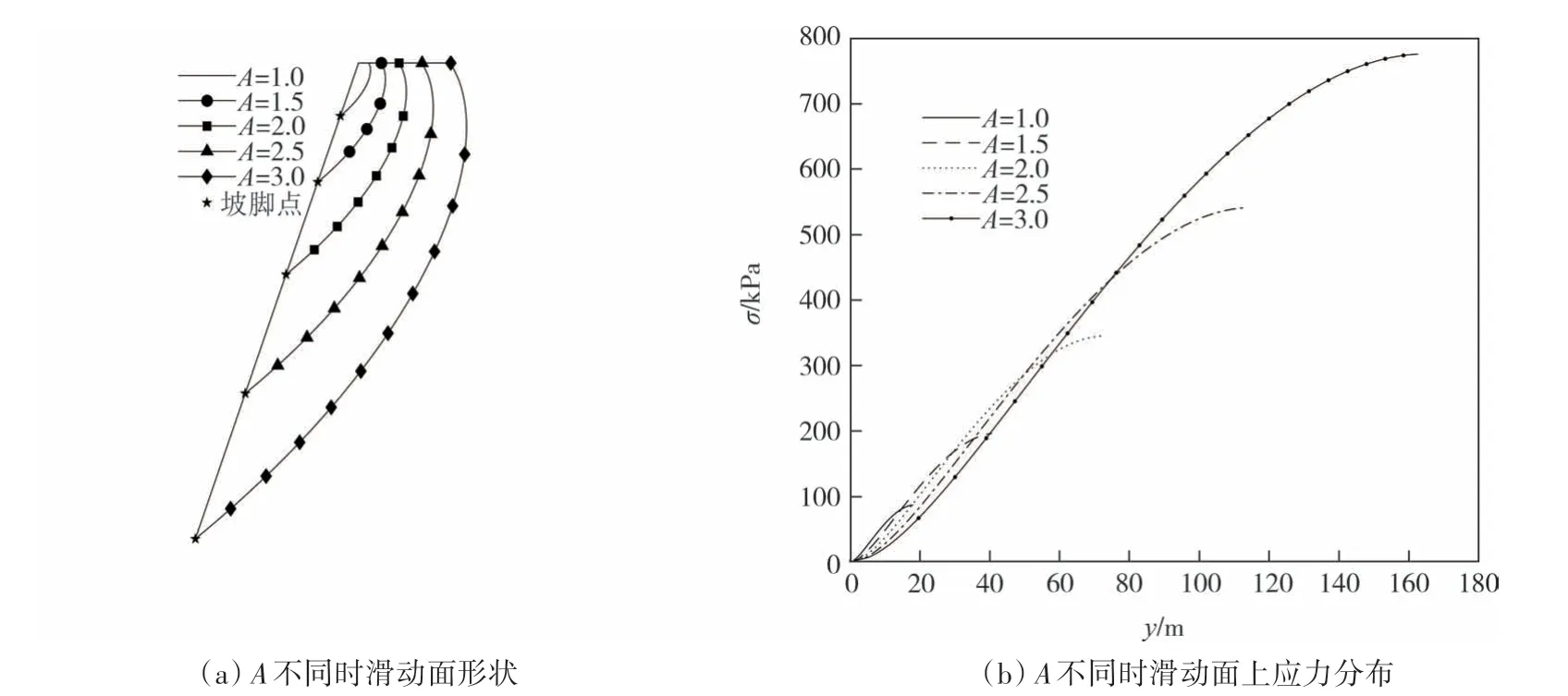

5 结论

