考虑双重沉积模式的多孔介质中颗粒三维迁移模型研究

刘晓明 ，涂树杰 ，阳栋 ，杨泽曦 ，刘涛

（1.湖南大学 土木工程学院，湖南 长沙 410082；2.中国建筑第五工程局有限公司，湖南 长沙 410004；3.中交公路规划设计院有限公司，北京 100088）

多孔介质中悬浮颗粒的迁移规律研究在地下水回灌［1］、核废料处置［2］、反滤层设计［3］、地下污染物迁移［4］等领域具有重要意义，是当前环境岩土工程领域一个重要的研究方向［5］.

国内外学者对多孔介质中颗粒迁移过程及机理的研究已开展了较多的工作.Ahfir 等［6］提出了一种描述脉冲注入颗粒物在多孔介质中的迁移及沉积特性数学模型.Bedrikovetsky 等［7］提出了考虑弥散效应及颗粒物尺寸阻滞作用的深层颗粒物迁移数学模型，并基于土柱试验与传统模型进行了对比.陈云敏等［8］建立了污染物在层状土中的一维扩散模型，通过分离变量法得到了解析解，阐明了污染物迁移击穿防污屏障的内在机理.试验研究方面，陈星欣等［9］通过室内土柱试验探讨了悬浮颗粒的浓度对其在饱和多孔介质中迁移和沉积特性的影响.刘泉声等［10］通过模拟试验研究了颗粒粒径对多孔介质中悬浮颗粒迁移-沉积特性的影响，并根据粒径比不同将悬浮颗粒在多孔介质中的迁移-沉积类型划分为滤饼过滤型、迁移-沉积型、自由迁移型三种.

经典颗粒迁移模型认为多孔介质中的悬浮颗粒沉积是吸附作用造成的.Sakthivadivel 等［11］发现，当悬浮颗粒粒径与多孔介质粒径比值大于0.05 时，存在显著的筛滤作用（即悬浮颗粒粒径大于多孔介质的孔隙吼道尺寸，形成的筛滤沉积）.而Bradford等［12］研究表明，悬浮颗粒中位粒径与多孔介质粒径比值大于0.005的低粒径比时，筛滤作用依然发挥着重要的作用.因此，在低粒径比时，同时考虑颗粒筛滤作用和吸附作用的预测结果与试验结果更为接近.处理因筛滤作用而产生的额外沉积机制的一种方法是假设存在双重沉积模式，即筛滤效应沉积与吸附效应沉积.对于双重沉积模式的研究，Simoni 等［13］通过将颗粒划分为两个子群，并赋予不同的碰撞效率值，成功描述了沉积颗粒浓度随深度非指数分布现象.Tufenkji 等［14］提出了考虑“快”和“慢”颗粒沉积共同影响的双沉积模式，提高了颗粒迁移沉积的预测精度.Katzourakis 等［15］通过拉普拉斯变换方法求得了双重沉积模式下颗粒迁移一维解析解，更好地拟合了现有的实验数据.由于考虑双重沉积后，问题求解变得复杂，这些研究都是在一维条件下进行的，不符合颗粒迁移的空间特性.

本文采用双重沉积模式下的沉积动力学方程，考虑附着颗粒的再释放和大颗粒的筛滤效应对颗粒迁移的经典模型进行修正，建立可同时考虑筛滤效应沉积与吸附效应沉积的多孔介质中颗粒三维迁移模型；然后通过拉普拉斯变换和傅里叶变换及其逆变换求得颗粒三维迁移模型的通解，得到点源和圆形面源注入条件下半无限空间颗粒迁移的解析表达式，并通过解的退化及对突破曲线的参数反演验证了解的正确性；最后，基于导得的解析解，对圆形面源恒定浓度注入情况下的水动力弥散系数、筛滤系数、吸附系数、释放系数等参数对颗粒迁移过程的影响机理进行了详细的分析.

1 颗粒迁移三维控制方程及通解

1.1 控制方程建立

考虑饱和均匀流场中的对流、三维水动力弥散和颗粒沉积效应，多孔介质液相中悬浮物颗粒运输的质量平衡方程为：

式中：C是液相中的悬浮物浓度，量纲为ML-3；t为时间，量纲为T；v为孔隙流体平均流速，量纲为LT-1；x为平行于流动方向的空间坐标，量纲为L；y，z为垂直于流动方向的空间坐标，量纲为L；Dx，Dy，Dz分别为x，y，z方向上的水动力弥散系数，量纲为L2T-1；n为孔隙率，量纲为1；C*为单位体积内沉积的颗粒总质量，量纲为ML-3.C与C*均为变量t、x、y、z的函数.

影响多孔介质中颗粒沉积的机制主要有两种，即大颗粒的筛滤作用和小颗粒的吸附作用［11，16］.图1是两种颗粒筛滤作用和吸附作用的示意图.

图1 筛滤作用与吸附作用示意图Fig.1 Schematic diagram of adsorption and sieve filtration

单位体积内沉积的颗粒总质量C*与筛滤作用沉积项C1*和吸附作用沉积项C2*的关系为：

其中，筛滤作用沉积项C1*被认为是不可逆的，而吸附作用沉积项C2*是可逆的.颗粒沉积动力学方程可以描述为：

式中：kstr为筛滤系数，量纲为T-1，与粒径比呈指数相关［17］；kat=3(1 -n)vαη/2d50为颗粒吸附系数，量纲为T-1，其中，d50为多孔介质的平均粒径，α为颗粒吸附效率，η为收集效率，其计算公式见文献［18］；kde为颗粒释放系数，量纲为T-1.

式（1）右侧第一项为对流项，体现了颗粒迁移的渗流作用.式（1）右侧最后一项为颗粒沉积项，由沉积动力学方程式（2）～（4）共同控制，本文的颗粒迁移模型是由式（1）～（4）联合建立的，因此考虑了渗流和颗粒迁移/沉积的耦合作用.

假设初始时多孔介质中无颗粒，颗粒从半无限空间表面注入，相应初始条件和边界条件可表示为：

初始条件式（5）（6）表示多孔介质中既无沉积颗粒，也无悬浮颗粒.边界条件式（7）表示在半无限空间表面注入强度随时间变化的颗粒注入源.边界条件式（8）～（10）为半无限域的理想情况.

需要指出的是，考虑极限情景下细颗粒可能无法穿透多孔介质，本文提出的颗粒迁移模型对颗粒的粒径应该有限定要求，参照文献［19-20］，限定细颗粒与多孔介质的粒径比小于0.1.当细颗粒粒径大于100 μm 时，颗粒的重力沉降较为明显，而本文模型中只考虑了对流与水动力弥散作用，因此应用本文模型时，细颗粒粒径应小于100 μm.

1.2 变换域的解

首先，通过拉普拉斯变换求得满足初始条件式（5）下方程式（3）的解为：

同理可求得方程（4）的解为：

将式（11）（12）对t求导后代入式（1）得到液相中悬浮物浓度表达式为：

式（13）需采用积分变换方法求解.对t和x进行拉普拉斯变换，变换变量为s和ω，对y和z进行傅里叶变换，变换变量为α和β.利用式（6）（7）可得变换域上的解为：

1.3 时空域的解

时空域中悬浮物浓度是通过对拉普拉斯域和傅里叶域的解进行反演得到的.首先对ω求拉普拉斯逆变换，使用拉普拉斯变换的位移性质、卷积定理和拉普拉斯变换表得到［21］：

将式（15）两边同乘2B⋅exp[(A-B)x]并运用边界条件（8）可以得到：

式中：L-1为拉普拉斯逆变换算子为任意函数f0(t)的拉普拉斯变换；a为任意常数；I0为零阶第一类修正贝塞尔函数.

假设：

式中：I1为一阶第一类修正贝塞尔函数.

对exp(-Et)进行两次傅里叶逆变换，得到：

最后，根据傅里叶变换的卷积定理，由式（17）（24）（27）得到考虑双重沉积条件下悬浮颗粒浓度的三维解析解：

2 半无限空间表面注入颗粒问题解析解

将边界条件式（7）的颗粒注入函数g(t，y，z)可以表示为：

式中：W(y，z)为颗粒注入源的几何形态；G(t)为颗粒的注入方式.

2.1 点源注入颗粒

当颗粒注入源为点源时，颗粒注入源的几何形态可表示为：

式中：δ(⋅)为Dirac delta 函数；y0和z0为点源的坐标.

将式（31）（32）代入式（28），利用Dirac delta 函数的筛选性质可得点源注入情况下颗粒迁移的解析解：

2.2 面源注入颗粒

假定半无限多孔介质表面局部区域D内，在t=0时刻连续注入浓度随时间t变化G(t)的颗粒.那么多孔介质内部颗粒物的迁移过程相当于无数个强度为G(t)dydz点源注入情形下颗粒物迁移过程在空间上的叠加.于是，多孔介质内颗粒的浓度可由式（33）在空间域上通过积分求得，此即源函数法的基本思想［23］.因此

考虑半无限体表面圆形区域连续注入浓度随时间变化的颗粒（圆心为O，半径为a）的情形.假定垂直水流方向水动力弥散系数相等（即Dy=Dz=Dr），而平行水流方向水动力弥散系数为Dx，此时颗粒浓度场可采用圆柱坐标（x，r）来表示，式（35）可写成：

将式（36）对变量φ进行积分，并注意贝塞尔函数的性质，整理后可得：

3 颗粒迁移解析解验证

3.1 解的一维退化

当颗粒注入源半径a=∞时，式（38）方便地退化成一维情形.

式中：tp为注入时间；Ω(t，x，r)为式（40）中G(τ)=C0的特殊情况.

对于瞬时注入颗粒情况，有：

式中：I=m/(nvS)为面源强度，量纲为MTL-3；m为注入颗粒质量，量纲为M；S为面源面积，量纲为L2；t'为颗粒注入的时刻，量纲为T.

利用Dirac delta 函数的筛选性质，式（40）可以转化为：

令式（43）中t'=0，kstr=0 和kde=0，即可得到基于经典对流弥散模型的颗粒迁移解析解［24-25］.

3.2 验证1：恒定浓度注入

本节采用式（40）（41）对Syngouna 等［26］的试验进行分析，并与单重沉积模式颗粒迁移解析解进行对比，以检验双重沉积模式颗粒迁移解析解的正确性.Syngouna 等［26］进行了两种流速（v=1.21 cm/min 和0.74 cm/min）下两种黏土颗粒（高岭石（KGa-1b）和蒙脱石（STx-1b））在填充玻璃珠的水平柱中的运输试验.柱直径D为2.5 cm，长L为30 cm，孔隙率n为0.42，其他相关参数见表1.

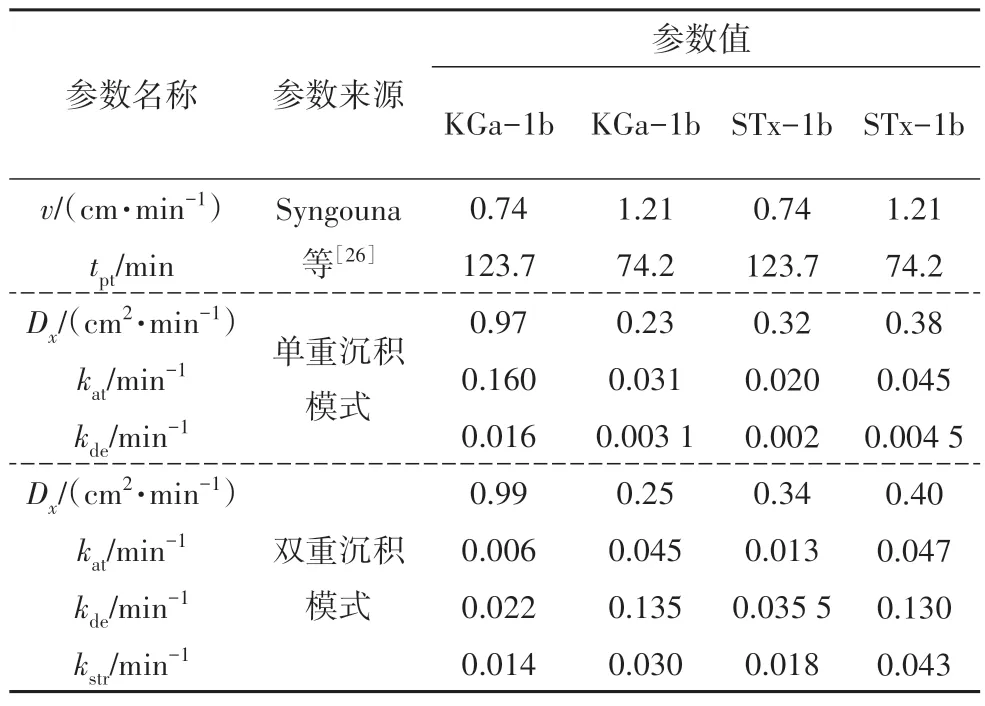
表1 恒定浓度注入时颗粒运输参数Tab.1 Particle transport parameters during constant concentration injection

试验数据的分析是通过PEST（Parameter Estima⁃tion）自动率定套件程序进行的.PEST 套件是基于GML（Gauss-Marquardt-Levenberg）算法开发的独立于模型参数估计和不确定性分析的综合软件，具有逆海森方法和最速下降法的优点，可以通过较少的模型运行次数，得到最优的参数结果［27］.采用PEST程序进行参数率定共分为三个步骤：

第一步为确定目标函数.本文采用单目标进行参数优化，以悬浮物理论流出浓度与实测流出浓度差的平方和最小为优化目标，目标函数公式为：

式中：f为目标函数；i为时段序号；m为总时段数；Cmod，i为第i时段的悬浮物理论流出浓度；Cobs，i表示第i时段的悬浮物实测流出浓度.

第二步为选择参数范围，为需要率定的参数选择合理的范围.需要率定的参数为Dx，kstr，kat，kde4个.

第三步为输入悬浮物实测流出浓度数据并执行迭代，输出率定的参数结果以及悬浮物理论流出浓度.

试验的突破曲线和单、双重沉积模式颗粒迁移解析解的计算结果如图2 所示（x=L=30 cm），相关参数见表1.对于Syngouna 等［26］考虑的两种流速情况，双重沉积模式解析解成功地拟合了KGa-1b 和STx-1b的突破曲线（x=L=30 cm），而相同条件下单重沉积模式下的解对该组试验数据的效果不理想，说明双重沉积模式下颗粒迁移解析解效果更优.

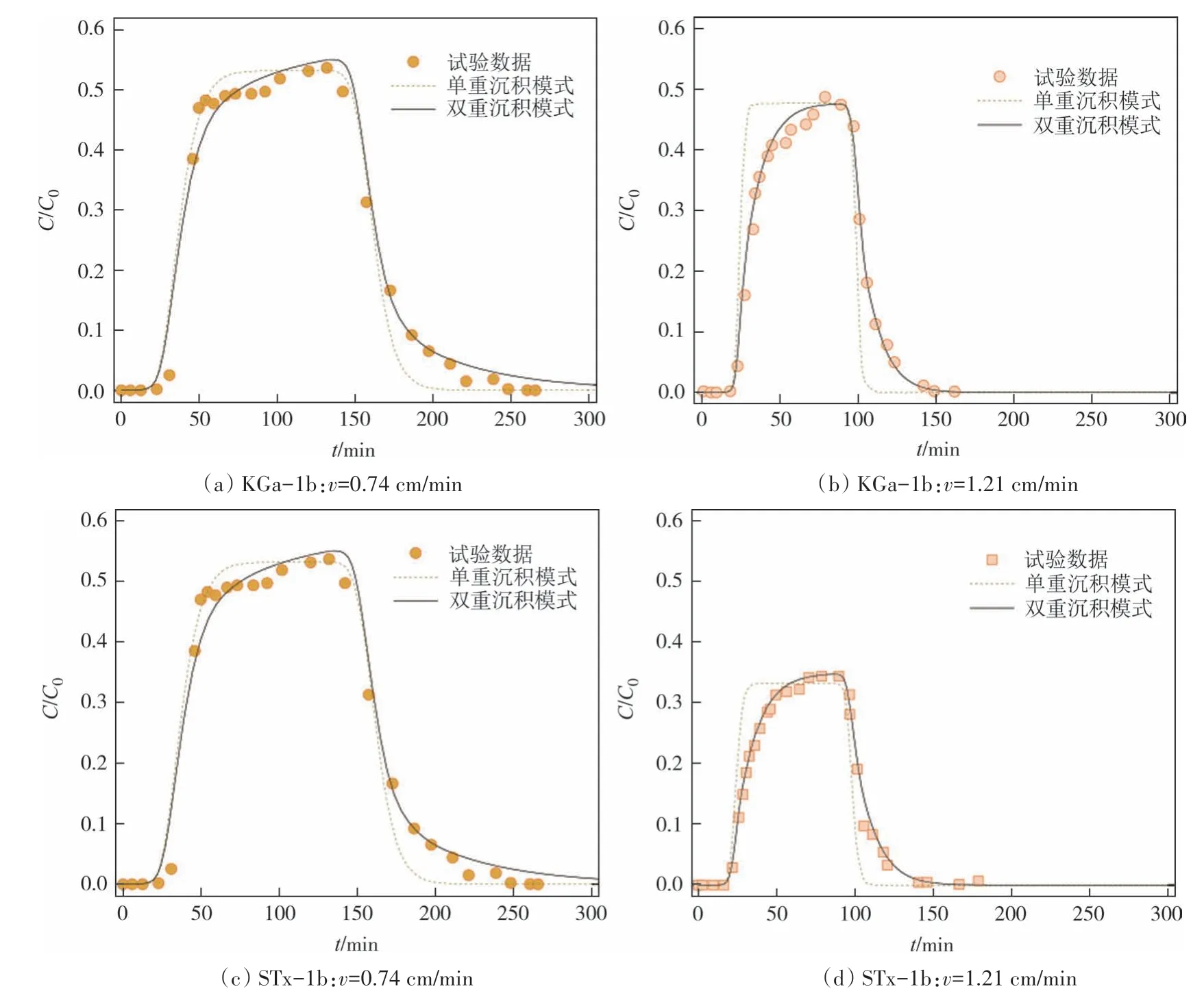
图2 恒定浓度注入时颗粒迁移突破曲线Fig.2 Particle migration breakthrough curve at constant concentration injection

3.3 验证2：瞬时注入

本节采用瞬时注入颗粒迁移解析式（43）对Bai等［20］的试验进行分析，并与单重沉积模式颗粒迁移解析解进行对比，以检验双重沉积模式颗粒迁移解析解的性能.试验数据的分析方法与3.2 节一致.Bai 等［20］进行了两种流速（v=0.384 cm/s 和0.576 cm/s）下两种粒径的球形二氧化硅颗粒（中值粒径D50=1.02 μm 和47 μm）在石英砂（D50=2.25 mm）柱中的运输试验.柱直径D为7 cm，长L为30 cm，孔隙率为0.45.

定义相对浓度CR=CVP/m，其中VP为柱的孔隙体积.试验的突破曲线和单、双重沉积模式颗粒迁移解析解的计算结果如图3 所示（x=L=30 cm），相关参数见表2.由图3 可知，解析式（43）可以成功模拟瞬时注入时颗粒迁移的突破曲线，且在颗粒粒径较大（D50=47 μm）时的性能比单重沉积模式下颗粒迁移解析解性能更好.通过分析可知，当悬浮物粒径为1.02 μm 时，粒径比远小于0.005，颗粒物沉积由吸附作用主导；当悬浮物粒径为47 μm 时，粒径比大于0.005，筛滤作用在颗粒物沉积过程中发挥着重要的作用，此时采用双重沉积模式的颗粒迁移模型效果更好.

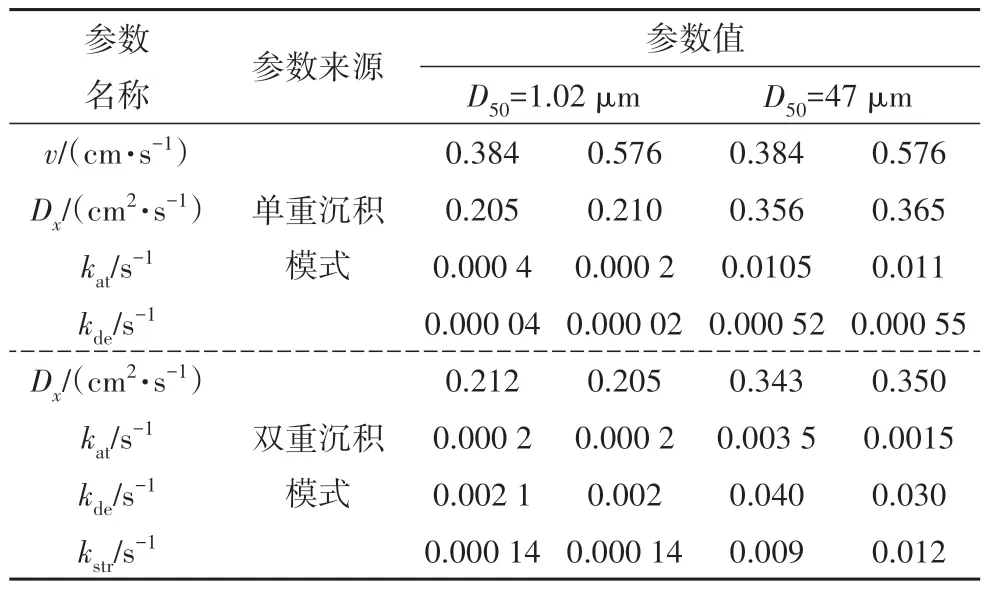
表2 瞬时注入时颗粒运输参数Tab.2 Particle transport parameters during instantaneous injection

图3 瞬时注入时颗粒迁移突破曲线Fig.3 Particle migration breakthrough curve during instantaneous injection

4 圆形面源注入时颗粒迁移规律

本节以圆形面源注入时的双重沉积模式颗粒迁移解析解［式（38）］来研究多孔介质中颗粒三维迁移规律.选择了恒定浓度注入这一典型的颗粒注入方式进行分析.

4.1 恒定浓度注入时颗粒迁移规律

参考文献［28］～［30］拟定计算参数：径向水动力弥散系数Dr=0.1 cm2/s，轴向水动力弥散系数Dx=1 cm2/min，渗流速度v=0.2 cm/min，筛滤系数kstr=0.02/min，颗粒吸附系数kat=0.01/min，颗粒释放系数kde=0.001/min.除特别说明外，本文算例均采用前述数值进行计算.

图4 为半无限多孔材料表面存在恒定浓度注入时悬浮颗粒物浓度演化（tp=200 min，a=5 cm）.引入无量纲浓度C/C0，由图4 可知，C/C0在深度方向和水平方向随着时间逐渐变化，由于深度方向存在渗流作用，颗粒物在深度方向的迁移速度明显快于水平方向.当时间较大（如tp=160 min）时，颗粒迁移过程逐渐稳定，颗粒物浓度在空间上的分布保持不变.

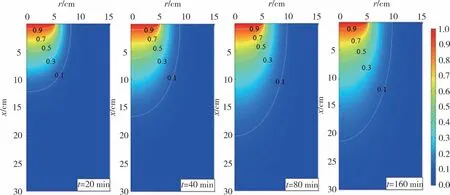
图4 恒定浓度注入时悬浮颗粒物浓度演化（tp=200 min，a=5 cm）Fig.4 Concentration evolution of suspended particles at constant concentration injection（tp=200 min，a=5 cm）

图5 给出了恒定浓度注入时颗粒迁移过程（tp=100 min，a=5 cm）.由图5（a）可知，在颗粒注入期间（ttp时），颗粒物浓度随深度增加依次达到峰值并快速下降.注入的颗粒物在对流和弥散作用下逐渐向多孔介质的深度和水平方向迁移并沉积.因此，在一定深度下，多孔介质中的颗粒物浓度会逐渐增加.深度越大，颗粒物浓度达到峰值的时间就越长，峰值浓度就越小.

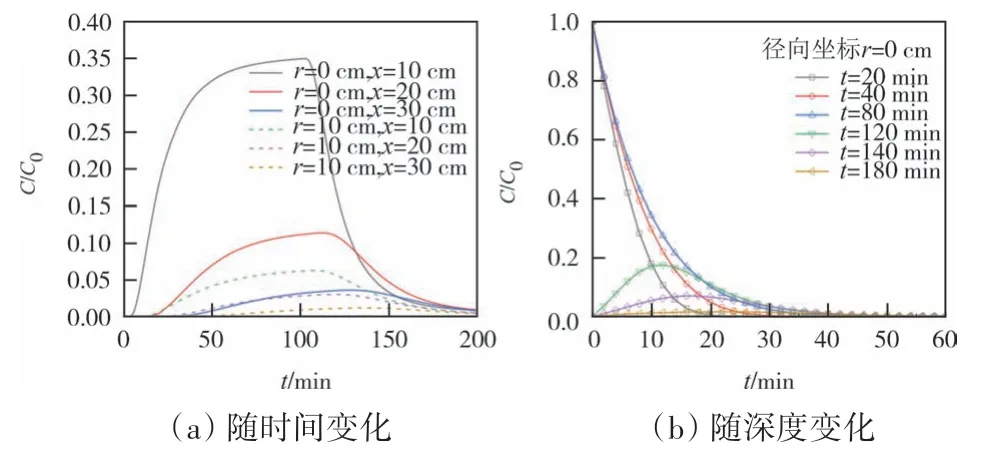
图5 恒定浓度注入时颗粒迁移过程（tp=100 min，a=5 cm）Fig.5 Particle migration process during constant concentration injection（tp=100 min，a=5 cm）

图5（b）为恒定浓度注入时（tp=100 min，a=5 cm）多孔介质中颗粒物浓度沿深度的分布.在颗粒注入期间（即t=20 min→40 min→80 min 时），多孔介质中颗粒物浓度随时间增大而增大，随深度增加而减小并趋于0.在颗粒停止注入后（即t=120 min→140 min→180 min 时），多孔介质表面颗粒浓度迅速下降，浓度峰值随时间增加而减小，峰值浓度所处的深度随时间增加而增加.

4.2 参数敏感性分析

为了进一步研究恒定浓度注入时颗粒迁移模型对各模型参数的敏感性，分别对参数Dx、kstr、kat、kde取不同值时的悬浮物突破曲线进行了计算（x=10 cm，tp=100 min），参数的敏感性分析结果见图6.

图6 恒定浓度注入时颗粒迁移敏感性分析（x=10 cm，tp=100 min）Fig.6 Sensitivity analysis of particle migration at constant concentration injection（x=10 cm，tp=100 min）

由图6 可知，悬浮物突破曲线存在峰值，颗粒浓度峰值随着参数Dx和kde值的增加而增加，随着kstr和kat值的增加而减小.通过分析可知，水动力弥散系数Dx值越大，颗粒弥散效应越显著，突破时间越快，而停止注入后（t>tp）的浓度越小.此外，kstr和kat越大，颗粒物在固体基质上的沉积越多，从而液相中颗粒峰值浓度越小；kde值越大，沉积颗粒从固体基质中脱离越多，从而导致液相中峰值浓度越大.

5 结论

1）建立了考虑筛滤效应与吸附效应的双重沉积模式颗粒三维迁移模型，利用拉普拉斯变换、傅里叶变换及其变换反演，导出了在一维渗流和三维弥散效应条件下颗粒迁移问题通解.给出了点源注入及面源注入颗粒时颗粒物浓度时空分布的解析表达式，并通过解的退化及对突破曲线的参数反演验证了解的正确性.

2）圆形面源恒定浓度注入情况下，在颗粒注入期间，多孔介质中颗粒物浓度随时间增大而增大，随深度增加而减小并趋于0.在颗粒停止注入后，多孔介质中颗粒物浓度随时间增大而减小，在深度上存在浓度峰值，浓度峰值所处的深度随时间增加而增加.

3）对面源注入情况下水动力弥散系数、沉积参数等的影响机理分析表明，水动力弥散效应加速了颗粒物的迁移，使颗粒突破时间变快，峰值浓度变高.筛滤系数kstr和颗粒吸附系数kat越大，颗粒释放系数kde越小，颗粒物在固体基质上的沉积越多，悬浮颗粒峰值浓度越小.