热-力耦合作用下能量桩单桩分析方法及工作特性研究

江杰 ，陈秋怡 ，欧孝夺 †，陈朝棋 ，张鹏

［1.广西大学 土木建筑工程学院，广西 南宁 530004；2.工程防灾与结构安全教育部重点实验室（广西大学），广西 南宁 530004；3.广西防灾减灾与工程安全重点实验室（广西大学），广西 南宁530004］

为积极推进“双碳”目标，有必要减缓建筑能源消耗.能量桩作为简便、经济及节能减排的新型桩基技术，满足上部结构承载性能需求的同时可充当热交换载体，能实现对浅层地热能的开发利用［1-3］.由于运行期间的桩体自由热变形受到周围土体的约束，导致桩身的力学和变形特性受到影响，近年来引起了国内外学者的广泛关注［4-6］.考虑能量桩在未来建筑领域的良好前景，但目前对其热-力耦合作用下的承载特性认识不足，因此研究能量桩的承载特性对建筑节能领域具有重要意义和工程价值.

目前能量桩承载特性的研究方法主要有试验、数值模拟和理论分析等.现场试验方面，Laloui 等［7］、Bourne-Webb 等［8］和Mccartney 等［9］首先在国外开展了一系列能量桩原位试验，研究热-力耦合作用下桩体内力变形特性，他们指出由温度荷载引起的附加应力会影响桩基的稳定性；桂树强等［10］和路宏伟等［11］在国内展开能量桩试验，研究了桩体温度变化引起的附加荷载和能量桩的荷载传递机制；孔纲强等［12］在南京市的能量桩现场试验也证明了温度变化会引起桩体应力、位移变化.鉴于现场试验费用高昂，试验条件难以控制，能够监测到的数据有限，因此一些学者［13-15］开始通过数值模拟研究能量桩单桩承载特性，通过模拟能量桩的运行情况，得出热-力耦合作用下桩基响应.模拟结果表明，温度变化使得桩身变形呈现热弹性，并会产生附加热变形和热应力.但数值模拟过于理想化，桩-土界面设置不准确，可能会与现场试验存在误差.

现有能量桩承载特性的理论分析方法主要是荷载传递法，荷载传递法需要借助描述桩-土界面关系的荷载传递函数［16］.Knellwolf 等［17］首先将荷载传递法应用于能量桩，分析了能量桩桩身应力、应变和位移，但迭代过程需要判断中性点位置，计算过于繁琐，可能导致结果不收敛；Pasten 等［18］选取折线型作为荷载传递函数，将温度变形考虑在桩段压缩量中，通过位移协调求解荷载传递方程；费康等［19］将温度荷载作用考虑到单元压缩量中，揭示了任意荷载-温度组合下的桩身变形、桩身内力分布，计算过程不需要对中性点进行预设，但忽略温度对传递函数的影响；Perić 等［20］和Olia 等［21］采用热弹性本构模型描述桩体的特性，结合边界条件推导了热-力耦合作用下桩身位移、应变和应力的解析解，并通过试验进行了验证，不足之处是解析解基于桩端位移为零的假设，不符合桩基实际.

本文在前人研究的基础上，对选用的荷载传递函数进行修正，开展能量桩单桩工作特性的研究.采用热弹性本构模型描述桩体的特性，通过桩侧土体与桩身之间的能量平衡关系，构建桩身位移控制方程，提出热-力耦合作用下能量桩单桩分析方法，该计算方法不需要进行复杂的受力分析且迭代不需预先假设中性点位置；通过试验验证该方法的正确性，并分析热膨胀系数、长径比及桩顶荷载水平对能量桩承载特性的影响，以期对能量桩的设计和发展提供参考.

1 热-力耦合作用下荷载传递模型

采用佐藤悟荷载传递模型［22］模拟热-力耦合下桩-土界面间的关系，桩-土相对位移表达式为：

式中：τ(z)、Δ分别为桩侧剪应力和桩-土相对位移；ks为侧阻传递系数，ks=τf/Δf，其中τf为极限摩阻力，Δf为摩阻力达到τf对应的桩-土相对位移，根据Fleming 等［23］建议的极限位移估算方法，建议Δf取0.5%D～2.0%D.

Mccartney等［24］认为温度作用下桩体胀缩会导致桩侧摩阻力发生变化，给出考虑温度荷载下的桩侧极限摩阻力公式，τf=σv[K0+(Kp-K0)KT]tanϕ，其中σv为上覆土压力；K0为静止土压力系数，K0=1 -sinϕ；Kp为被动土压力系数，Kp=(1+sinϕ)(1 -sinϕ)；ϕ为桩-土界面摩擦角；KT为考虑热应变的侧向土压力影响因子，KT=καTΔT[(D/2)/0.02L]，其中κ为土体抗膨胀经验系数；αT为桩身混凝土的热膨胀系数；[(D/2)/0.02L]为Reese 等［25］提出的几何归一化因子.

2 能量平衡方程

2.1 基本假定

1）根据Knellwolf 等［17］的分析，热-力耦合作用下桩径向变形较小，故计算分析只考虑一维轴向变形；

2）桩周土体性质、桩身混凝土弹性模量Ep和热膨胀系数αT不受温度变化的影响；

3）桩体遵循热弹性本构定律，桩体温度、桩身截面形状和材料性质沿桩长方向均匀分布.

2.2 桩身能量平衡方程

假定桩身在热-力耦合作用下不发生塑性变形，始终为热弹性变形，桩身所受外力及位移如图1 所示，地基中桩身总势能Π由桩身变形能Wu及势能增量Wp两部分组成，忽略桩侧土压力对桩体产生的横向变形，则桩身在轴向满足能量守恒.

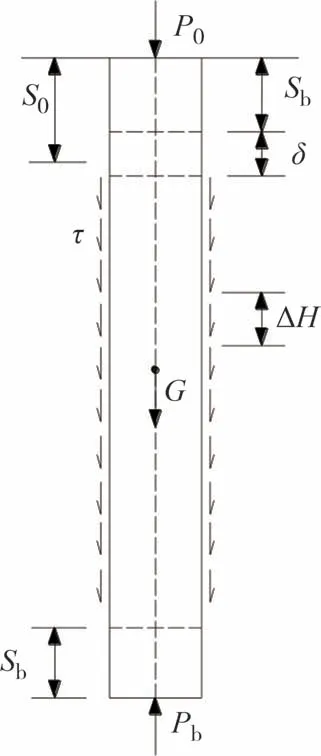
图1 桩身受外力及位移示意图Fig.1 Schematic diagram of external force and displacement of pile

取能量桩桩身本构关系为：

式中：σ为轴向应力；ε为轴向应变；ΔT为温度增量.

故考虑热-力耦合作用下的桩身变形能为：

桩体产生的势能增加为：

式中：dδ为桩身变形量；z为计算截面至桩顶的距离；m为桩身质量；g为重力加速度，取10 N/kg；H为桩身长度；Sb为桩端位移；ΔH为桩身重心变化量，ΔH=Sb+dδ/2.

桩的轴向总势能等于作用于桩身的外力所做功之和，有：

式中：W0、Wf和Wb分别为桩顶荷载P0、桩侧摩阻力以及桩端阻力Pb做功；S0和Sb分别是桩顶、桩端位移.

联立式（4）～（9）有：

桩身单元i受力变形如图2 所示.对于桩身单元i，存在下式关系：

图2 单元i受力及变形图Fig.2 Load and displacement of cell i

将式（12）和（13）代入式（11），整理可得：

式中：ΔPi和ΔPi+1分别为单元i上、下截面轴力增量；ΔSi和ΔSi+1分别为单元i上、下截面位移增量；U为桩截面周长.

桩身第i单元沿单元桩长单位面积上的摩阻力增量形式为：

接着考虑桩顶节点的轴力增量及桩端节点反力增量得到公式（23）（24）.

桩顶节点1：

联立式（22）、式（23）和式（25），将桩身各单元的刚度矩阵组装，得到桩的总刚度矩阵K为：

综上，可得到热-力耦合作用下能量桩工作特性的控制方程：

2.3 桩顶约束处理

根据能量桩实际运行情况，温度荷载作用导致桩身产生位移，上部结构的存在限制约束其位移.为反映该约束作用，在桩顶设置一个弹簧进行模拟.因此竖向力加载和温度加载须分开计算，竖向力加载中将桩顶视为自由，温度加载过程采用刚度系数为kt的弹簧模拟桩顶与上部结构的相互作用，得到式（28）.

2.4 数值实现

运行过程能量桩主要受上部结构的竖向力及与浅层地热能交换时的温度荷载，考虑温度加载中桩顶的约束作用，将能量桩承载特性计算分为竖向力加载、温度加载两个阶段.

2.4.1 竖向力加载

首先令ΔT=0，根据侧阻传递系数和土体参数构建初始化刚度矩阵，对控制方程（28）进行迭代求解获得桩身节点位移增量，最后基于节点位移增量得到桩身侧摩阻力增量、桩端阻力增量等.

2.4.2 温度加载

以竖向力加载结束时的桩基响应作为温度加载的起始状态，通过将温度荷载划分为若干增量步，采用刚度系数为kt的弹簧模拟温度加载中的桩顶约束作用，并对整体刚度矩阵进行修改，求解过程与竖向力加载一致，最后得到热-力耦合作用下能量桩的桩基响应.

3 理论模型的验证与分析

为验证提出能量桩承载特性计算方法的准确性，将计算结果分别与Ng 等［26］试验、Laloui 等［7］试验以及蒋刚等［27］在昆山现场试验进行比较.

3.1 算例1

3.1.1 算例概况

Ng 等［26］通过对中密砂土地基中的能量桩进行试验研究.取该模型试验的原型桩长为19.6 m，直径为0.88 m，桩体弹性模量为27.8 GPa，桩身热膨胀系数为2.22×10-5/℃，弹性模量和泊松比分别为11 MPa和0.2，摩擦角φ=31°，土层需要的计算参数见表1.

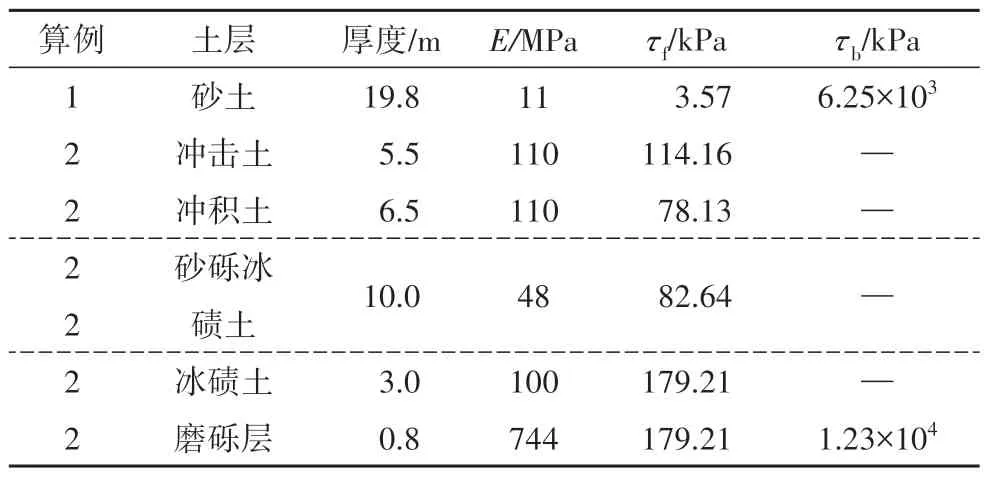
表1 荷载传递土层参数Tab.1 Soil parameters of load transfer

3.1.2 桩身轴力分布计算结果

为研究不同温度增量下桩身轴力分布规律，通过将计算结果与Ng 等［26］的试验结果进行对比，可以看出结果较一致.由图3 可知，桩身轴力分布规律呈现沿桩长先增大后减小的规律，原因主要是温度升高引起的负摩阻力致使桩身轴力随深度逐渐增大，并在负摩阻力与正摩阻力转折处达到峰值.此外，桩身轴力峰值出现在桩身0.6L处，与Laloui等［7］现场实测的桩身轴力峰值位置0.8L存在差异，差异的主要原因是桩端约束条件不同，Ng 等［26］为中密砂土层，弹性模量较小，Laloui 等［7］的桩端土层为砂土，刚度大，能提供更大的桩端约束，故桩身轴力峰值位置更接近桩端.

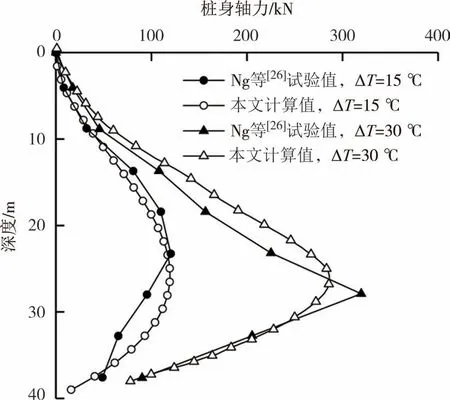
图3 温度荷载作用下桩身轴力Fig.3 Axial force of pile under thermal load

3.1.3 长径比的影响

蒋刚等［27］认为长径比会影响能量桩的桩身力学性能.为研究长径比对能量桩承载性能的影响，分别取3组不同的L/d（改变L，保持d不变），为方便对比，通过实际桩身轴力与自由膨胀时的轴力，定义β为桩身轴力影响系数，β=N/(αT⋅ΔT⋅EpAp)，其中N为桩身轴力.

为探究仅有温度荷载作用时L/d对桩身轴力影响系数的影响，图4 给出了桩身轴力影响系数沿桩长方向的变化规律.由图4 可知，当桩径比较大时，桩身中部轴力变化更明显，大致在桩身0.6L处达到峰值，然后逐渐减小，与Iodice 等［28］的分析结果趋势较一致.因此长径比会影响能量桩的轴力变化，且长径比越大，轴力积累效应越明显.故对于超长能量桩的施工建造中，要注意对地基中上部的维护.

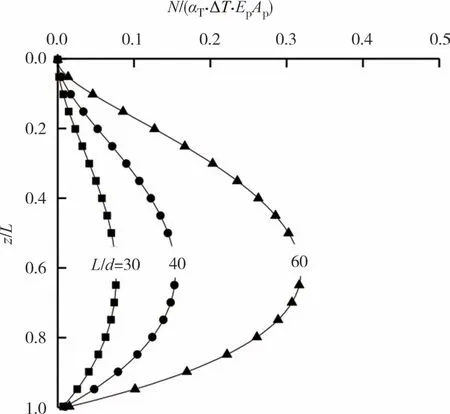
图4 不同长径比下桩身轴力分布Fig.4 Axial force distribution of pile under different L/d

3.2 算例2

3.2.1 算例概况

Laloui 等［7］在瑞士开展了能量桩现场试验.试验桩直径为0.88 m，桩长L=25.8 m，桩身弹性模量为29.2 GPa，热膨胀系数为1×10-5/℃.现场土层分布及所需要的参数如表1所示.

3.2.2 桩身应变计算结果验证

图5 为竖向应变沿桩长方向的变化曲线.将计算结果与桩身竖向应变（桩顶自由，无桩顶荷载）试验结果进行对比，可知桩身竖向应变计算值和实测值较一致，证实了提出计算方法的准确性.由图5 可以看出，桩身中上部竖向应变较大，中下部较小.由于桩顶部无约束导致自由热膨胀受到的约束小，故桩顶的热应变最大，数值上应接近自由膨胀量.温度增量为21 ℃时，桩顶的热应变计算值为-2.06×10-4，接近试验值-1.94×10-4，另外计算值和试验值的竖向应变的最小值皆出现在桩端附近.

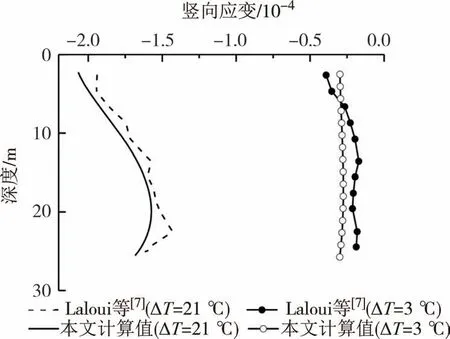
图5 温度荷载作用下桩身竖向应变Fig.5 Vertical strain of pile under thermal load

3.2.3 桩身混凝土热膨胀系数的影响

为进一步分析热膨胀系数（根据工程实际，常用热膨胀系数是（0.8～1.2）×10-5/℃对能量桩桩身内力的影响，根据Laloui 等［7］的现场试验，分析不同热膨胀系数下桩身侧摩阻力分布情况（规定桩侧摩阻力向上为正，向下为负），对比结果如图6 所示.可知，不同热膨胀系数的能量桩、桩侧摩阻力总体上呈现两端高、中部低的趋势.

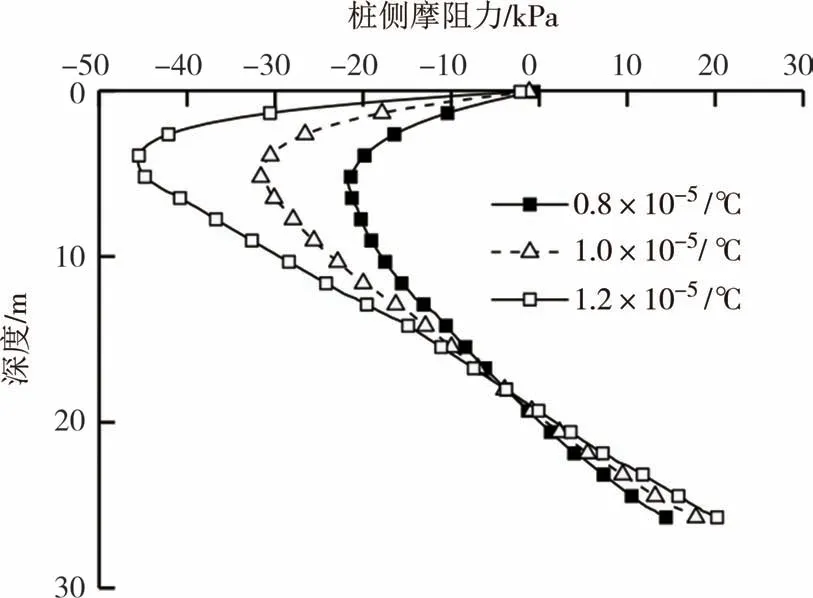
图6 不同热膨胀系数下桩侧摩阻力分布Fig.6 Lateral friction resistance distribution under different thermal expansion coefficient

纯温度荷载（ΔT>0）工况下，桩身上部受到向下的侧摩阻力，下部受到向上的摩阻力.由图6 可知，随着热膨胀系数的增大，桩侧摩阻力数值增加，对两端处影响较显著.其中热膨胀系数为1.2×10-5/℃工况下最大负摩阻力数值为-45.5 kPa，接近桩顶位置，最大正摩阻力数值为20.2 kPa，位于桩端附近；热膨胀系数为0.8×10-5/℃工况下最大负摩阻力数值为-21.5 kPa，接近桩顶位置，最大正摩阻力数值为14.4 kPa.因此，在实际能量桩工程中，不宜选用过大热膨胀系数的混凝土作为桩身材料.

3.3 算例3

为研究荷载-温度作用下能量桩的承载变形特性，蒋刚等［27］在江苏昆山开展了能量桩现场试验，并对不同荷载工况下能量桩桩身内力进行了分析.根据文献［11］可知，能量桩桩长40 m，长径比为66.7，桩体弹性模量30 GPa，热膨胀系数为1.0×10-5/℃，土层分布的参数如表2所示.

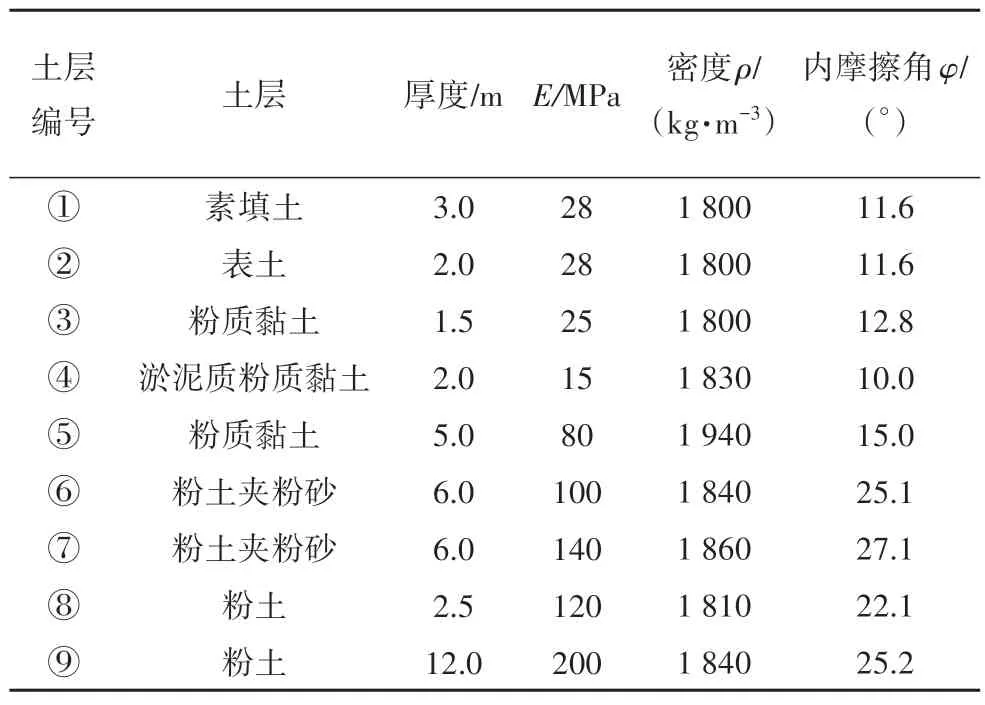
表2 土层分布的参数Tab.2 Parameters of soil layer distribution

根据现场试验数据，理论计算分别验证荷载-升温和荷载-降温两种工况下能量桩桩身轴力及侧摩阻力分布情况，具体见图7和图8.

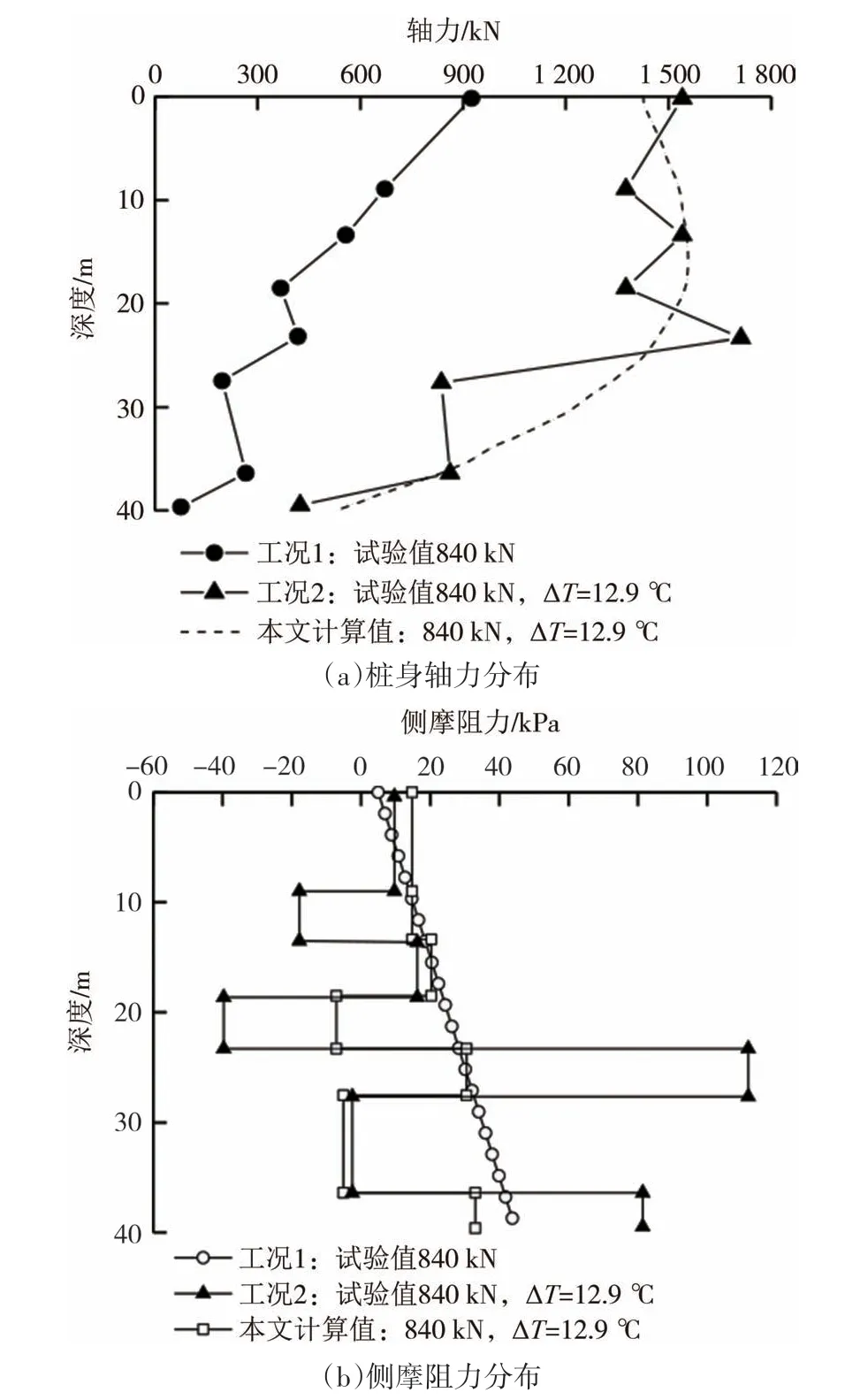
图7 荷载-升温工况下桩身轴力及侧摩阻力分布曲线Fig.7 Distribution curves of axial force and shaft resistance under mechanical and thermal loads（heating）

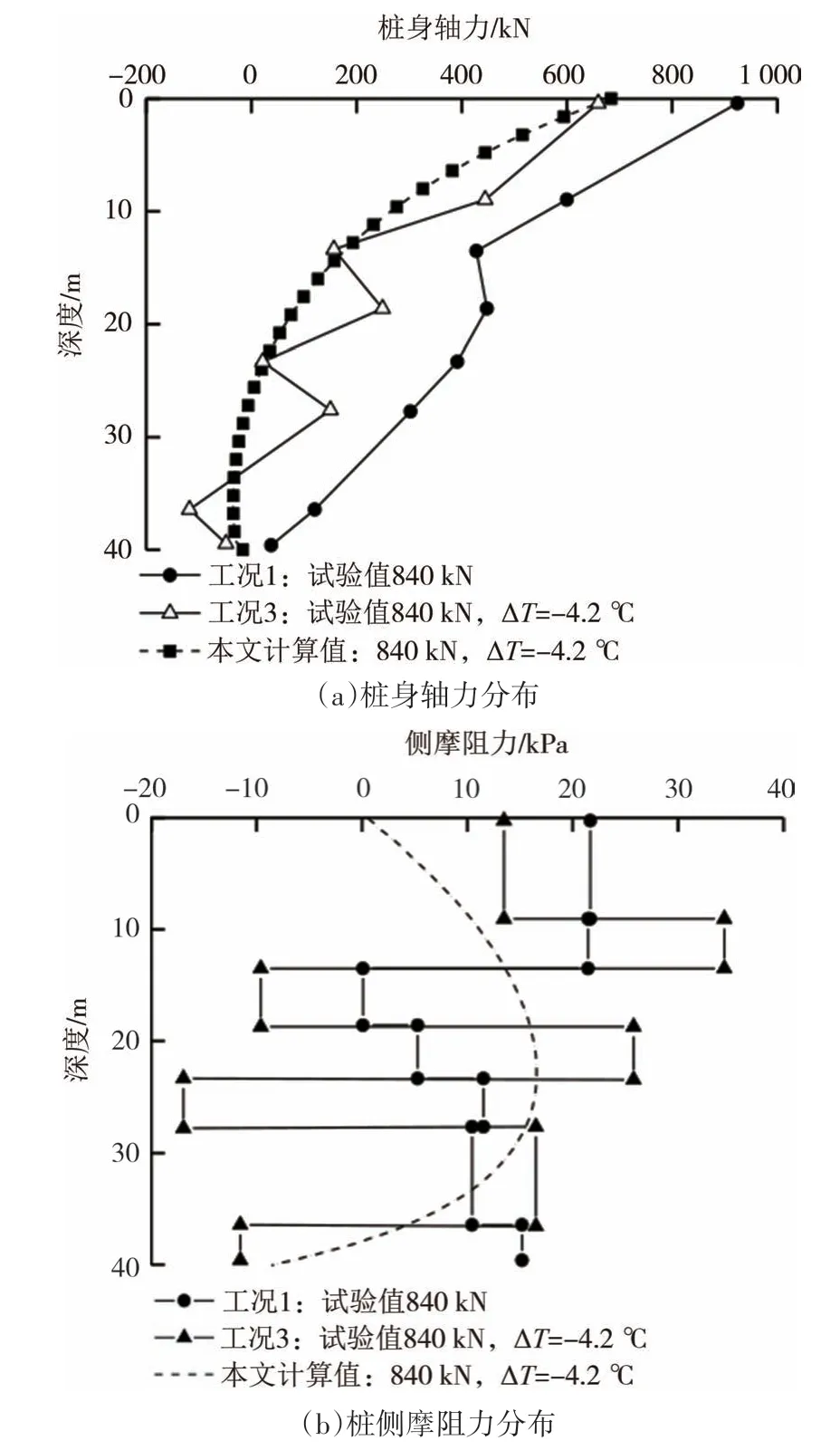
图8 荷载-降温工况下桩身轴力及侧摩阻力分布曲线Fig.8 Distribution curves of axial force and shaft resistance under mechanical and thermal loads（cooling）

3.3.1 荷载-升温工况下的荷载传递特征

图7 给出了静力荷载为840 kN、温度升高12.9 ℃工况下的桩身轴力和桩侧摩阻力沿桩长方向的分布图（桩顶弹簧系数一般可在0～10 GPa/m 之间取值，取1 GPa/m）.由图7可知，桩身轴力及侧阻力计算结果与试验值结果趋势一致，对比工况1和工况2，可以发现温度荷载会对轴力和摩阻力分布产生影响.

由图7（a）和图7（b）可知，温度升高使得桩身轴力和桩侧摩阻力数值上与单一力学荷载存在差异.计算求得的桩侧摩阻力随着桩长方向近似线性增大，由于桩端土层为粉土，刚度小，导致桩端阻力的增加有限，故在桩端附近桩侧摩阻力的增加幅度有所降低.

3.3.2 荷载-降温工况下的荷载传递特征

通过试验结果和计算结果的对比，研究荷载-降温工况下桩身轴力及桩侧摩阻力分布规律.与荷载-升温工况对比，可知温度降低引起桩身收缩，桩身的荷载传递特征发生了变化.由图8（a）可知，将工况1与工况3 对比发现桩身轴力有所差异，温度降低使得桩身轴力呈现沿深度逐渐减小，在桩端附近轴力为负值.因此，在工程中要注意对桩身下半部分防护.从图8（b）可以看出，工况1 只有桩顶荷载，桩侧摩阻力皆为正值，与计算结果进行对比可知，温度变化引起的桩身收缩会受到桩周土体约束，导致桩侧摩阻力呈现先增加后减小的分布规律，到桩端附近出现桩侧摩阻力为负值，与工况3试验值一致.

3.3.3 桩顶荷载的影响

根据文献［25］，取极限荷载为4 500 kN，为分析桩顶荷载对单桩承载力的影响，分别对不同荷载工况，升温15 ℃和降温15 ℃的单桩内力变形进行研究，具体如表3所示.

表3 荷载-温度工况计算方案Tab.3 Calculation scheme of thermo-mechanical coupling

图9和图10分别给出了不同荷载下升温工况和降温工况的桩身轴力随深度分布曲线.可以看出，荷载-升温工况下，桩身轴力随深度变化规律与Bourne-Webb 等［8］现场测试和Ouyang 等［29］的计算值得到的规律较为接近.此外可以看出，桩身温度变化导致桩体膨胀，上部结构的存在约束向上膨胀的趋势导致桩顶处轴力增大.从图9可知，100%Pu下桩顶轴力最大，约为4 660 kN.荷载-降温工况下，桩身轴力总体上呈现沿深度逐渐减小趋势.当桩顶荷载水平较小时，桩端附近存在受拉区；随着桩顶荷载的增大，桩身下半部分受拉区长度逐渐减小.

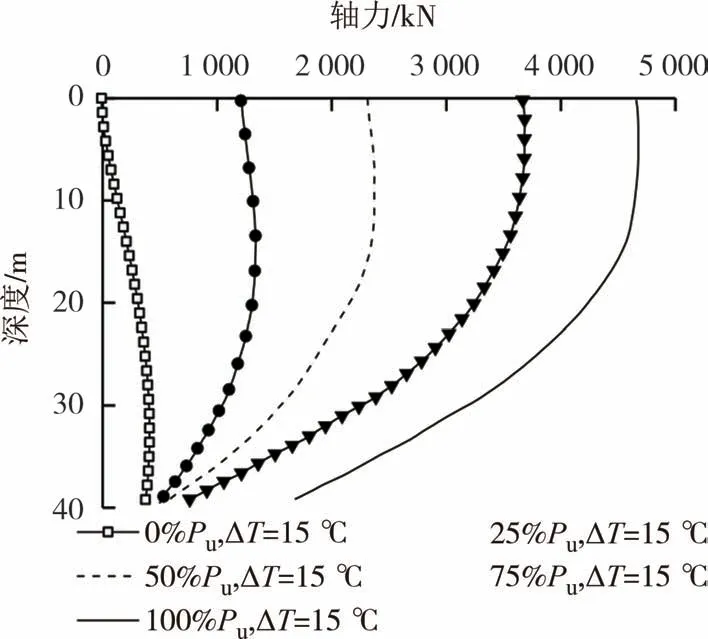
图9 不同荷载工况下桩身轴力分布曲线（升温）Fig.9 Axial force distribution curve under different mechanical load conditions（heating）

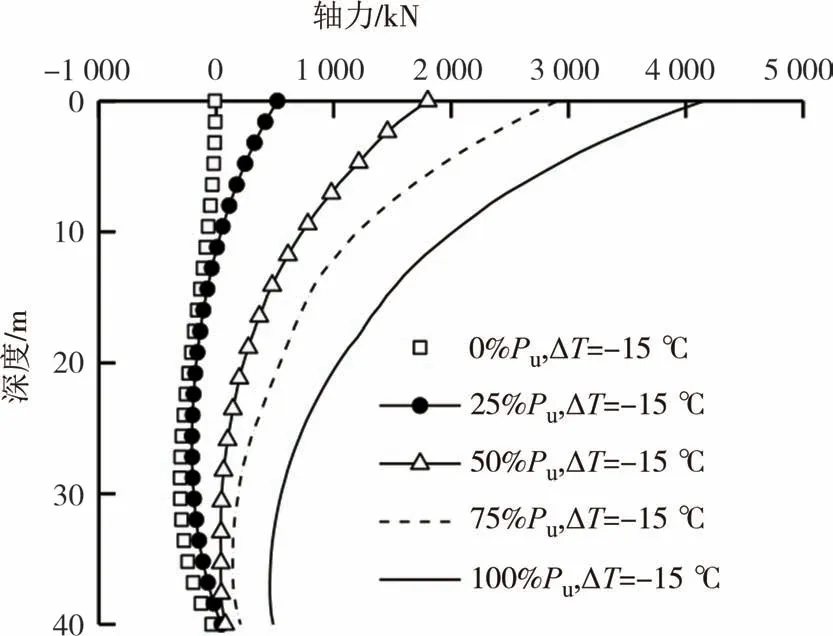
图10 不同荷载工况下桩身轴力分布曲线（降温）Fig.10 Axial force distribution curve under different mechanical load conditions（cooling）

3.3.4 桩顶沉降变化

为研究温度荷载对桩顶沉降的影响，图11 给出了单一荷载、荷载-升温和荷载-降温工况下桩顶沉降变化曲线.由图11 可知，三种工况下桩顶沉降变化规律趋于一致.相对于纯力学荷载和工况5，荷载-升温工况下桩顶沉降较小.为研究温度荷载对桩顶沉降的影响，定义沉降幅度λ=|s1-s0|/s0× 100%，其中s0为纯力学荷载作用下桩顶沉降，s1为荷载-升温/降温工况下桩顶沉降.

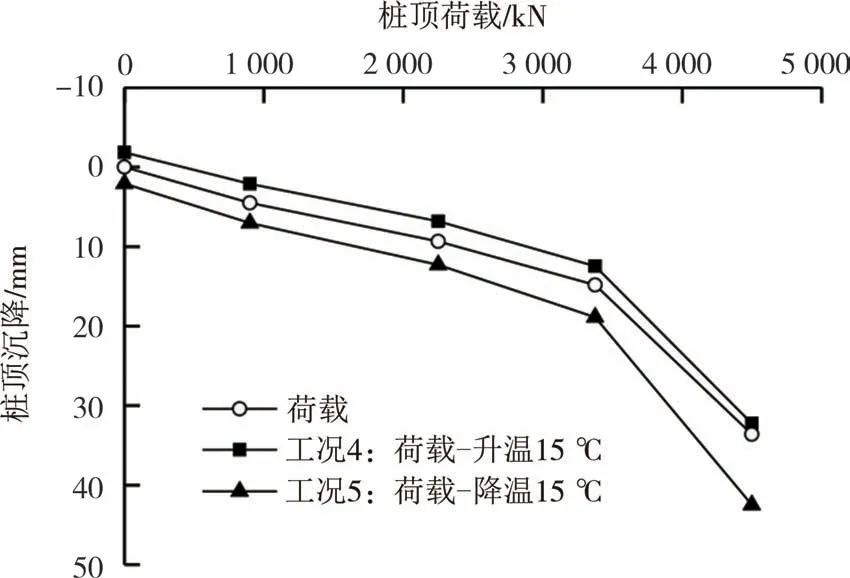
图11 桩顶荷载-沉降曲线Fig.11 Load-settlement curve of pile top

对荷载-升温工况下桩顶沉降变化进行分析可知，当桩顶荷载为0%Pu、25%Pu和50%Pu时，桩顶沉降量分别为-1.84 mm、2.10 mm 和6.82 mm；25%Pu和50%Pu作用下对应的沉降幅度分别为53%和27%.可以看出，随着桩顶荷载的增加，沉降幅度逐渐减小，表明温度效应对桩顶沉降的影响有所降低.对荷载-降温工况下桩顶沉降变化分析，可以看出，0%Pu、25%Pu和50%Pu时，桩顶沉降量分别为2.09 mm、7.02 mm 和12.30 mm；当桩顶荷载为25%Pu和50%Pu时，桩顶沉降增加幅度达到55%和31%.此外，随着桩顶荷载的增加，沉降值逐渐增大.整体上，当桩顶荷载较低（≤25%Pu）时，温度荷载对桩顶沉降的影响较大，这与蒋刚等［27］数值模拟得到的规律一致.

此外，分析荷载趋于0 时（即处于单一温度工况），工况4和工况5桩顶沉降变化.可知前者桩顶沉降为负值（取向下为正），后者桩顶沉降为正值，说明升温使桩身膨胀导致桩顶位移向上，而降温使桩身收缩导致桩顶位移向下.

当桩顶荷载大于75%Pu时，荷载-降温工况下桩顶沉降量为42.50 mm，接近极限值.因此，作为能量桩使用的工程桩基应当控制桩顶荷载水平.

4 结论

本文基于荷载传递法，通过描述桩侧土体与桩身之间的能量平衡关系，构建桩身位移控制方程，提出了热-力耦合作用下能量桩单桩分析方法，主要结论如下：

1）桩体采用热弹性本构模型，通过考虑温度对传递函数的影响，基于荷载传递法和能量平衡原理提出热-力耦合作用下能量桩工作特性的分析方法，理论推导过程无需进行复杂的力学分析，求得的计算结果能够反映能量桩的工作特性，可为类似工程提供参考.

2）荷载-升温工况下，随着桩顶荷载逼近极限值，桩顶处轴力数值上变化明显；荷载-降温工况下，当桩顶荷载水平较低时，桩身存在受拉区，且随着桩顶荷载的增大，受拉区长度逐渐减小.

3）桩顶自由条件下，对桩身热膨胀系数和长径比的分析表明，随着热膨胀系数增大，桩侧摩阻力数值上有所增加，且桩顶和桩端附件受热膨胀系数影响更为明显；随着长径比的增大，轴力积累效应明显，当L/d等于60 时，能量桩桩身轴力影响系数最大达到0.32.

4）桩顶约束条件下，对不同桩顶荷载下的桩顶沉降分析表明，当桩顶荷载较低时（≤25%Pu），温度效应的影响更显著，而当桩顶荷载大于75%Pu，桩顶沉降量临近极限值，此时需要注意桩基承载性能.