建筑物对塔机顺风向风力干扰效应研究

林其涛

(中铁城建集团第一工程有限公司 山西太原 030024)

1 引言

塔机相较于单体状况下塔机的风力可能会发生很大变化。塔机作为桁架结构，它的尺度相对于建筑物尺度非常小，不同风向角下，建筑物对塔机的风载荷影响会很大[1]。而关于塔机结构干扰效应的国内外规范中，也仅仅给出了通过结构充实率和间隔比来计算塔机局部相同结构0°风向角下干扰因子的方法[2-3]。

针对干扰效应的研究手段主要分为风洞试验和CFD数值仿真[4]。李正良等[5]基于高频动态天平风洞试验，得到了格构式塔架在不同遮挡间距、不同风速工况下的横风向、顺风向、基底弯矩功率谱和扭转向基底力。杨风利等[6]设计了多种输电塔塔身模型并进行风洞试验和CFD数值仿真，获得了不同模型背风面风荷载降低系数(干扰因子)随高宽比的变化规律。Martin等[7]运用风洞试验建立了碟形天线对通信塔塔身基底力的干扰因子计算方法。以整体基底力和基底弯矩来定义干扰因子往往比较宏观，不能进一步了解干扰规律在结构上的分布特征[8]。基于周围建筑物群体不同布置密度，Quan等[9]通过测压风洞试验研究并分析了低矮房屋屋顶风压分布特征。Yu等[10]和Yan等[11]分别基于测压试验得到了方形截面和多边形截面的高层建筑物迎风面、背风面和侧面在不同横向和纵向间距比下干扰因子分布规律。余文林等[12]基于CFD方法对冷却塔在不同风向角下的干扰效应进行了数值模拟。

研究建筑物对塔机局部结构的风载荷干扰因子，对于更清晰地认识干扰机理和指导塔机抗风设计具有重要意义。本文通过建立不同风向角和不同横向、纵向间距比下的塔机和建筑物CFD数值计算模型，得到了塔机局部结构上的风力系数，系统研究了塔机局部结构在不同建筑物位置和不同风向角下的顺风向风力干扰效应，得到了塔身标准节和起重臂臂节的干扰因子分布规律。

2 CFD数值模拟方法

将塔机沿高度方向和水平方向进行分区，以不同分区的风载荷特性来表征塔机局部风载荷特征，从而建立塔机局部结构风载荷特性。共划分成35个分区，图1为塔机模型分区图。

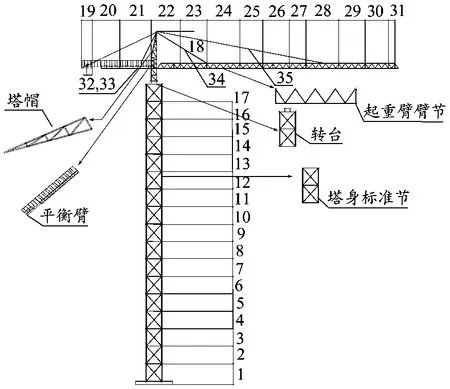
图1 QTZ125塔机模型分区

塔机总高度为H＝55 m，建筑物简化为30 m×30 m×40 m的方柱。为满足塔机回转、变幅和起升等作业要求，建立建筑物与塔机位置。B为塔机塔身标准节的宽度，X为塔身中心与建筑物的横向距离，Y为塔身中心与建筑物的纵向间距。

2.1 计算域与边界条件

2.1.1 计算域及其网格

计算域设置为内切圆直径800 m，高度200 m的正十二面棱柱，改变入流面和出流面的位置实现不同的风向角，计算域如图2所示。计算网格采用六面体和四面体混合网格，中间通过金字塔单元过渡连接。在塔机和建筑物表面生成边界层网格，第一层网格厚度分别为0.001 8 m和0.002 8 m。本文基于y+值和网格无关性验证得到网格总数量3 500万左右。

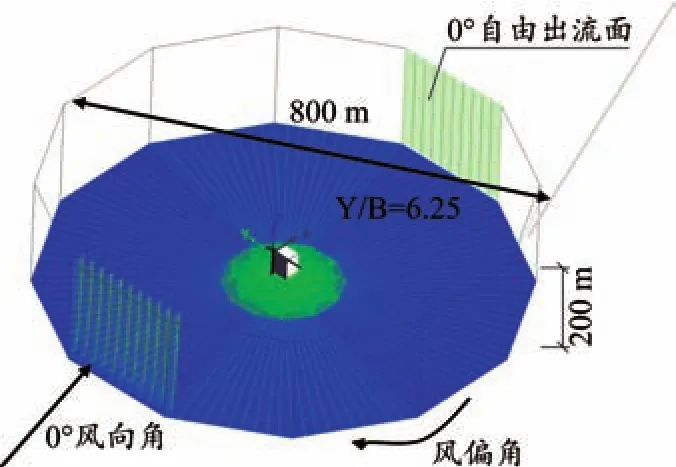
图2 模型计算域

2.1.2 边界条件

湍流模型选取Realizable k-ε。基于大气边界层特性来定义入口边界条件的平均风速剖面、湍动能k和耗散率ε，其中以标准B类地貌、10 m高度处的风速13.3 m/s来定义风速剖面。出口边界条件为自由出流。塔机表面、建筑物表面和计算域地面为非滑移壁面，采用非平衡壁面函数，其余面为对称面。采用SIMPLE算法对速度压力耦合方程进行求解，离散格式为二阶迎风格式。

2.2 风力系数定义

图3为塔机风向角示意图。根据坐标系，定义塔机风力系数为:

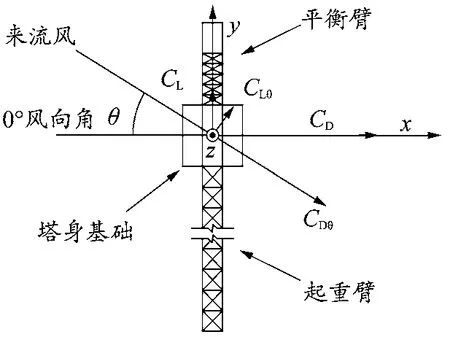
图3 塔机风力方向

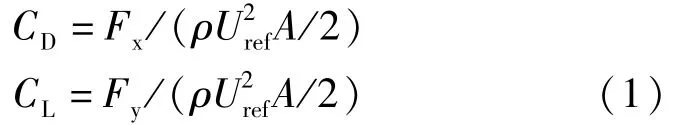
式中，CD、CL为塔机沿坐标系方向上的风力系数；Fx、Fy为塔机沿坐标系方向承受的风载荷；ρ为空气密度(kg/m3)；Uref为参考高度处的风速(m/s)；A为结构迎风面面积(m2)。

不同风向角下，风力系数均是基于塔机体轴坐标系。为了建立沿着风向角下的风力系数，需对坐标系进行转换。在风轴坐标系下，风向角为θ时，塔机顺风向风力系数CDθ为:

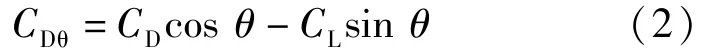
2.3 干扰效应量化

为分析建筑物对塔机风力干扰效应程度的大小，采用干扰因子IF来量化。干扰因子定义为:

式中，CDθ，I为有建筑物存在时，塔机顺风向平均风力系数；CDθ，P为塔机单体情况下顺风向平均风力系数。

当IF＝1时，建筑物对塔机风力没有干扰；当｜IF｜＜1时，建筑物遮挡效应占主导作用，IF值越小则遮挡效应越明显；当｜IF｜＞1时，建筑物对塔机风力表现为放大效应，IF值越大则放大效应越明显。其中，当出现IF＜0时，说明建筑物的存在使得塔机顺风向风力方向偏转180°。

3 风力干扰研究

为验证本文数值计算的可靠性，将计算得到的边界条件和建筑物迎风面风压分布特征分别与相关规范进行对比得出，无建筑物遮挡时数值模拟风场的入口及距离塔机前10 m处的风速剖面u/u10(u为某高度处的风速，u10为10 m高度处的风速)及湍流强度Ⅰ与理论风场值保持良好的一致性，且说明风场具有较好的自保持性。风场中有建筑物遮挡时，在180°风向角下建筑物处于塔机的上游，其迎风面风压系数CP＝p/(ρu2/2)(p为迎风面上的风压)分布特征不受塔机的影响，建筑物迎风面风压系数分布特征与规范较好的吻合。

3.1 建筑物不同位置的影响

建筑物位置是影响干扰效应的一个主要原因。在满足塔机现场作业要求的前提下，本文将塔机沿建筑物纵向和横向布置，共分为5种位置。对5种位置下的干扰效应进行了研究。

3.1.1 塔身标准节干扰因子分析

塔身由15节标准节组成，随着高度的变化，塔身标准节的干扰因子呈现多种变化特征。在210°和240°风向角下，5种位置下的塔机塔身标准节均被建筑物完全遮挡，即干扰因子均接近于0；在300°和330°风向角下，由于建筑物的截面是正方形，即干扰因子的表现特征分别类似于60°和30°风向角下，所以本文以0°到180°和270°风向角来对塔身标准节的干扰因子进行分析。图4为不同位置下的塔身标准节干扰因子沿高度分布情况，其中z/H为塔身标准节中心高度与塔机总高度的比值。

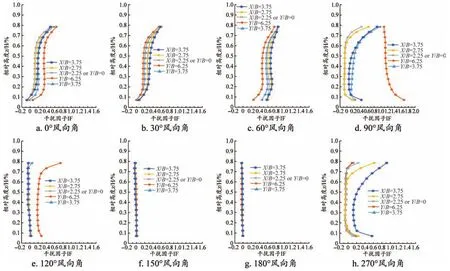
图4 塔身标准节干扰因子沿高度分布

0°风向角下，5种位置下的干扰因子均小于1，遮挡效应占主导作用。随着横向间距比的缩小，干扰因子逐渐减小。这是因为风吹过塔机，在塔机上游形成高压区，在其下游形成低压区。同时，由于塔身标准节的空间格构形式，风经塔机继续向下游的建筑物流动，在建筑物迎风面前端形成高压区。塔机越靠近建筑物，即其越靠近建筑物迎风面前端的高压区，从而使得塔机的压差阻力越小即风力系数越小，导致干扰因子随着减小。随着纵向间距比的缩小，干扰效应也逐渐减小。这是因为风流经建筑物，在其迎风面中间位置会形成驻点区域，在驻点两侧形成流动方向相反的气流，并在建筑物拐角处发生气动分离，越靠近拐角，气流速度越大，使得塔机风力系数增大，进而干扰效应减小。30°和60°方向角，5种位置下的干扰因子表现出相同的特征。其中，在z＝0.6H附近区域时，出现风力干扰因子增大拐点，建议在此位置处安装扶墙，增强塔机的抗风性能。

0°、30°和60°风向角下的塔身标准节干扰因子沿高度分布呈现三次函数变化特征。对其进行非线性拟合，表达式为:

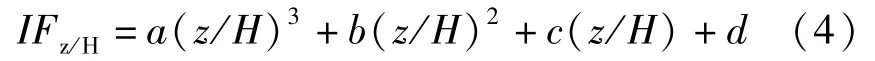
式中，α、b、c、d为拟合参数；z/H为相对高度。

采用最小二乘法进行拟合，拟合结果与计算数据的相关系数均大于95%，表明塔身标准节干扰因子与相对高度具有很好的三次函数关系。

90°风向角下，横向间距比为X/B＝2.25和X/B＝2.75时，塔身标准节干扰因子随横向间距比的增大而变化不明显，但在横向间距比为X/B＝3.75时，干扰因子随横向间距比的再次增大而明显变化，说明横向间距比超过了临界值，使得干扰因子发生较大的变化。随着纵向间距比的增大，塔身标准节干扰因子随之逐步增大，但当塔机处于建筑物边沿时，建筑物对塔身的干扰效应由遮挡效应转变成放大效应，这是因为此风向角下，来流风在建筑物边沿区域形成风加速区，使得塔机承受的风载荷大于单体情况下。270°风向角下，不同横向间距比下的塔身标准节干扰因子沿高度的分布情况与90°风向角下保持一致，但是纵向间距比下发生了较大的变化，这是因为此时塔身处在了建筑物风场的更下游，使得纵向间距比的变化对干扰因子的影响较90°风向角下的小。

120°风向角下，纵向间距比为Y/B＝6.25时，塔机位于建筑物的边沿处，气流在建筑物拐角处分离，形成加速气流作用在塔身标准节上，从而使得其干扰因子大于0，而在其他间距比下，塔身标准节完全被建筑物遮挡，使得干扰因子近乎为0。同样，在150°和180°风向角下，由于建筑物的遮挡，塔身标准节的干扰因子也为0。

3.1.2 起重臂臂节干扰因子分析

图5为起重臂不同横向和纵向间距比下的风力干扰因子分布。0°、30°和60°风向角下，起重臂臂节干扰因子接近于1，说明横向间距比和纵向间距比对塔机起重臂臂节的干扰效应影响较小。这是因为建筑物处于塔机的下游，且起重臂高于建筑物，从而使得间距比对起重臂的干扰很小。90°风向角下，由于起重臂远端处于风场的下游，受到建筑物的影响使得远端处的起重臂臂节的干扰因子小于1，表现为遮挡效应；而在270°风向角下，起重臂远端处于风场的上游，建筑物干扰很小，因此干扰因子接近于1。在这两种风向角下，起重臂近端均受到建筑物的干扰，干扰因子均大于1，表现为放大效应，其中在90°风向角下，随着横向间距比和纵向间距比的增大，干扰因子增大，在270°风向角下，随着横向间距比的增大，干扰因子缩小，而随着纵向间距比的增大，干扰因子增大。

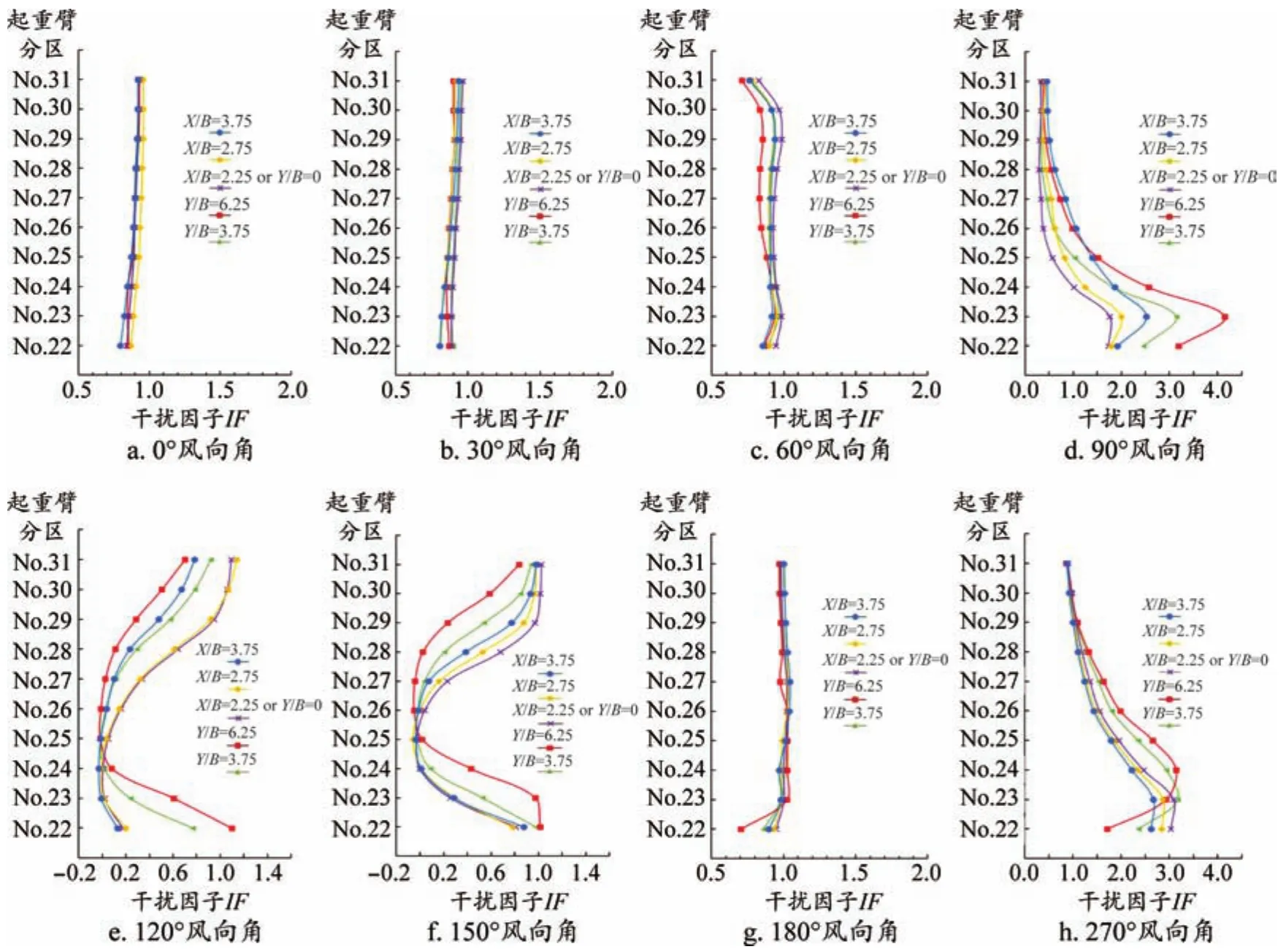
图5 起重臂臂节干扰因子分布

3.2 不同风向角的影响

建筑物对塔机风力干扰效应的研究中，风向角也是一个主要影响因素。基于相同横向或者纵向间距比，本文对0°到330°共12个风向角下的塔身标准节和起重臂臂节干扰因子进行了分析。

图6为12个风向角下的塔身标准节干扰因子沿高度的分布规律。从图中可以看出，横向间距比X/B＝2.25，X/B＝2.75和X/B＝3.75下，塔身标准节干扰因子均小于1，建筑物表现为遮挡效应，其中60°和300°风向角下的干扰因子最大，IF值在 0.6 附近波动；120°、150°及对应的 210°、240°风向角下，由于建筑物的遮挡占主导作用使得干扰因子始终最小，IF值接近于0。风向角从0°到60°变化中，塔身干扰因子随之增大。90°至270°风向角下的干扰因子因为建筑物的遮挡效应占主导地位使其IF值很小，但是在X/B＝3.75时，因建筑物遮挡效应减弱，使得塔身标准节干扰因子增大。

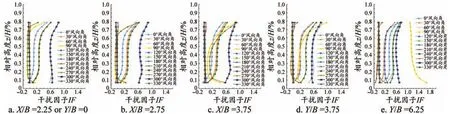
图6 12个风向角下塔身标准节干扰因子

风向角从0°到60°变化中，随着纵向间距比的逐渐增大，60°风向角下塔身标准节干扰因子始终最大，但是30°风向角下的塔身标准节干扰因子在纵向间距比Y/B＝0时大于0°风向角下，在Y/B＝3.75时而与0°风向角下相同，在Y/B＝6.25时而小于0°风向角。在纵向间距比Y/B＝3.75时，60°和300°风向角下干扰因子最大，IF值在0.6附近波动。由于建筑物的遮挡，120°至240°风向角下的塔身标准节干扰因子沿高度的增加变化不大；在Y/B＝6.25时，最大干扰因子出现在90°风向角下，这是最不利的风向，应当引起格外关注。

图7为起重臂臂节干扰因子随风向角的变化图。从图中可以看出，在不同的横向或者纵向间距比下，起重臂臂节的干扰因子IF值在1附近波动，但是在 90°、120°、150°和 270°风向角下的变化尤为突出，表明起重臂臂节对上述风向角比较敏感，其中在120°和150°风向角下，起重臂臂节干扰因子表现为遮挡效应，而在90°和270°风向角下，近端起重臂臂节干扰因子始终表现为放大效应，应当引起关注。由于建筑物对末端起重臂臂节的影响逐渐减弱，12个风向角下的起重臂臂节干扰因子波动逐渐减小，IF值逼近于1。

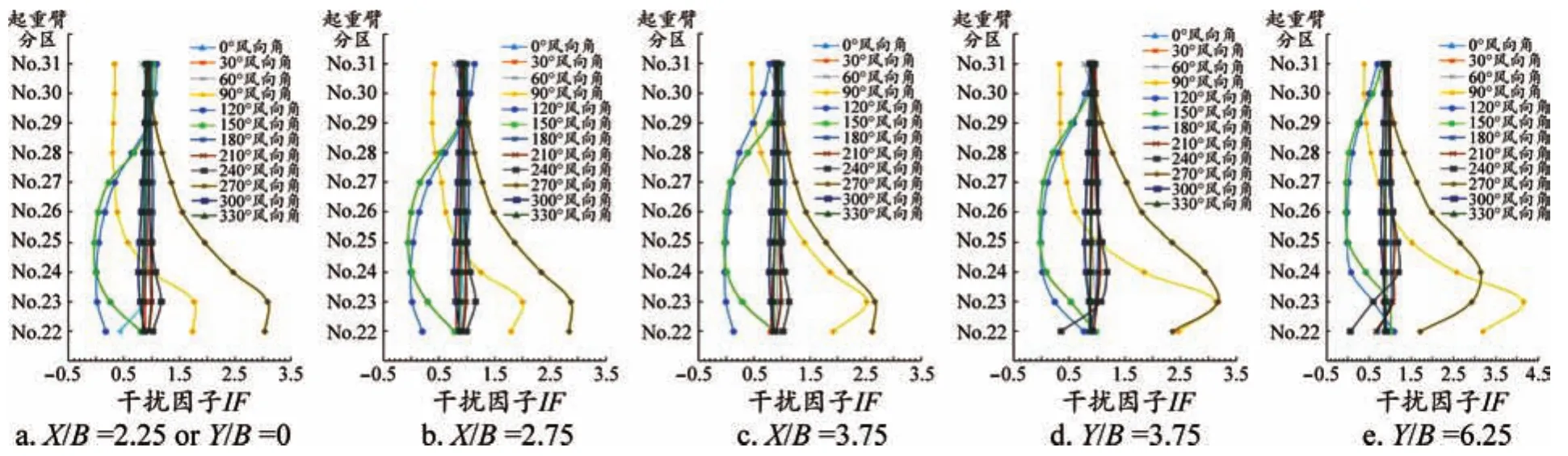
图7 12个风向角下起重臂臂节干扰因子

4 结论

本文系统分析了塔机与建筑物在不同的横向和纵向间距比下及不同风向角的塔机风力干扰因子分布规律，得到了如下结论:

(1)不同的横向或者纵向间距比及在不同的风向角下，建筑物对塔机的干扰效应主要表现为遮挡效应。

(2)0°、30°和 60°风向角下，塔身标准节风力干扰因子随着横向间距比和纵向间距的增大而增大，并且干扰因子沿高度的分布规律符合三次函数特征；同时在这三种风向角下，不同的横向间距比和纵向间距比对起重臂臂节干扰因子的影响很小，可以忽略，但是在120°和150°风向角下，起重臂臂节在不同的横向或者纵向间距比下干扰因子分布规律符合二次函数特征，中间段臂节遮挡效应最为明显，干扰因子接近于0。

(3)不同的横向间距比下，塔身标准节干扰因子在60°或者300°风向角下最大且值在0.6附近，但在纵向间距比Y/B＝6.25时，90°风向角下的干扰因子最大且大于1，表现为放大效应。

(4)在不同的横向或者纵向间距比下，起重臂臂节干扰因子IF值在1附近波动，且起重臂臂节对90°、120°、150°和 270°风向角比较敏感。在 120°和150°风向角下，起重臂臂节干扰因子表现为遮挡效应，而在90°和270°风向角下，近端起重臂臂节干扰因子始终表现为放大效应。