射流管阀控液压马达参数辨识建模与故障诊断

于黎明, 周洁华

(北京航空航天大学 自动化科学与电气工程学院, 北京 100191)

引言

液压伺服作动器HSA因其稳定性好、推重比大等特点,仍然是现役飞机的主选作动器[1-3]。射流管阀控HSA由于射流喷嘴的结构特点,油液不容易产生堵塞,具有抗污染能力强的优点;但同时大泄漏量带来较大的能量损失[4-5]。当故障发生会给维修带来巨大困难和成本,目前已经研究出诸多先进的故障诊断算法,如:数字模型监控、深度学习和人工智能等,姜云春等采用最小二乘支持向量机的方法建立液压伺服系统模型,检测其与实际输出间形成的残差信息,实现了对液压伺服系统的故障诊断[6]。刘红梅等[7]针对液压位置伺服系统,提出基于双级径向基函数的神经网络模型,利用第一级函数对故障进行检测,使用第二级网络对系统的典型故障进行定位,于此同时还改进了K均值聚类算法来优化、神经网络结构、加快了网络的收敛速度、减少了网络计算量。唐勇等[8]将神经网络运用到动态流量的软测量当中,提出了一种基于动态流量测量的电液伺服系统故障诊断方法,取得了很好的实时诊断效果。但是航空作动器实际应用中多数采用的是实时模型自监控的方法,存在虚警率高的问题[9-10]。

本研究以某航空应用的射流管阀控液压马达为研究对象,针对射流管伺服阀、滑阀和液压马达等关键部件,采用机电液综合系统较为常用的AMESim软件建立其仿真模型,结合实验数据对该模型进行参数辨识以精准化仿真模型;采用此仿真模型进行BP神经网络故障诊断算法研究与分析,基于采样数据进行网络训练所需特征量提取与故障诊断,通过仿真结果与实验数据对比,验证了本研究建立的射流管阀控液压马达仿真模型以及BP神经网络故障诊断算法的有效性。

1 射流管阀控液压马达数学模型

射流管阀控液压马达结构原理图如图1所示,由力矩马达、射流管接收器、滑阀、液压马达等组成。向液压马达输入指令角度, 经过控制部分会向力矩马达线圈输入所对应的指令电流,在极化和控制磁场的作用下,线圈内会产生偏转力,从而带动衔铁和流管喷嘴的偏转,喷嘴离两侧接收器的距离不再相等,两侧接收的流量也不一致,从而产生压力差引起阀芯向一侧运动。阀芯运动改变阀芯阀套之间的开口度,输出放大的流量压力信号来带动液压马达转动,进而带动舵面偏转。利用RVDT测量输出转角,与指令信号形成闭环,通过PID调节进行反馈控制。

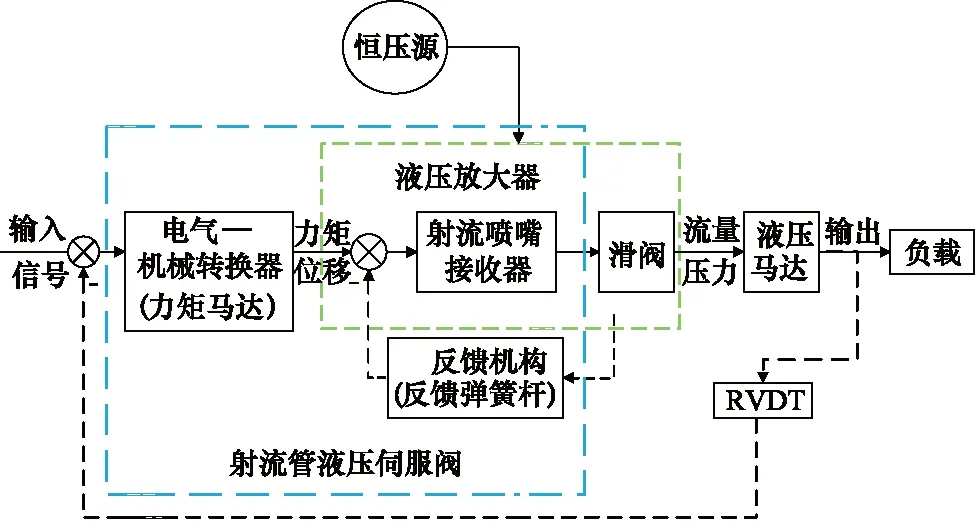
图1 射流管阀控液压马达工作原理Fig.1 Basic structure and working principle of jet pipe valve-controlledhydraulic motor

针对力矩马达、射流管阀、液压马达的工作原理分别建立如下分部件的数学模型,以组成射流管阀控液压马达系统模型,分述如下:

1) 力矩马达

电磁力矩方程:

Td=KtIC+Kmθ

(1)

式中,Kt—— 力矩马达的力矩系数

IC—— 力矩马达输入电流

Km—— 力矩马达的弹簧刚度

θ—— 力矩马达偏转角度

力矩平衡方程:

(2)

式中,Ja—— 伺服阀力矩马达和射流喷嘴的转动惯量

t—— 伺服阀工作时间

Ba—— 衔铁组件黏性阻尼系数

Ka—— 反馈弹簧管的刚度

2) 射流管阀

射流管阀的线性化流量方程为:

QL=Kqxj-KcpL

(3)

式中,QL—— 射流放大器的负载流量,定义

Qr—— 阀芯右腔的流量

Ql—— 阀芯左腔的流量

Kq—— 射流放大器的流量增益

Kc—— 射流放大器的流量-压力系数

pL—— 射流放大器的负载压差,等于阀芯左右两腔的压力差,即pL=pr-pl

主阀芯右腔内的流量连续性方程为:

(4)

对应的左腔为:

(5)

式中,As—— 两腔的端部面积

V0—— 两腔的初始油液体积

βe—— 油液体积弹性模量

pl,pr—— 接收孔-阀芯左、右腔压力

滑阀阀芯的动力学方程为:

(6)

式中,mv—— 滑阀的阀芯质量

Bv—— 阀芯的运动黏性阻尼系数

滑阀负载流量方程:

Qf=KQxv-KCpf

(7)

式中,Qf—— 滑阀的输出流量

pf—— 滑阀的输出负载压力

KQ—— 滑阀的流量增益

KC—— 滑阀的流量-压力系数

3) 液压马达

液压马达的流量连续性方程:

(8)

式中,θm,Dm—— 液压马达的转角、排量

Ctm—— 液压马达的总泄漏系数

Vt—— 工作容积

液压马达的动态力矩平衡方程为:

(9)

式中,Jm—— 液压马达和负载折算到马达轴上的转动惯量和

Bm—— 油液黏性阻尼系数

G—— 负载的扭转弹簧刚度

TL—— 外负载力矩

2 仿真与实验验证

在实际测控平台中研究故障诊断,需要在实体作动器中注入故障才能获取故障数据,而注入故障需进行破坏性的参数修改,才能通过故障实验获取到故障诊断所需原始数据。这种做法不仅操作复杂,而且需要的成本及代价过高。为此,通过参数辨识将仿真模型准确化,使得仿真模型与实际作动器相契合,进而确保通过仿真获取的故障数据与实际故障数据更加吻合。

2.1 仿真建模

在数学模型的基础上,为方便对参数进行调整、获取故障诊断的原始数据,利用AMESim软件搭建完整的射流管阀控液压马达仿真模型如图2所示。代入相关参数,以经典PID控制调节输出角位移曲线如图3所示。

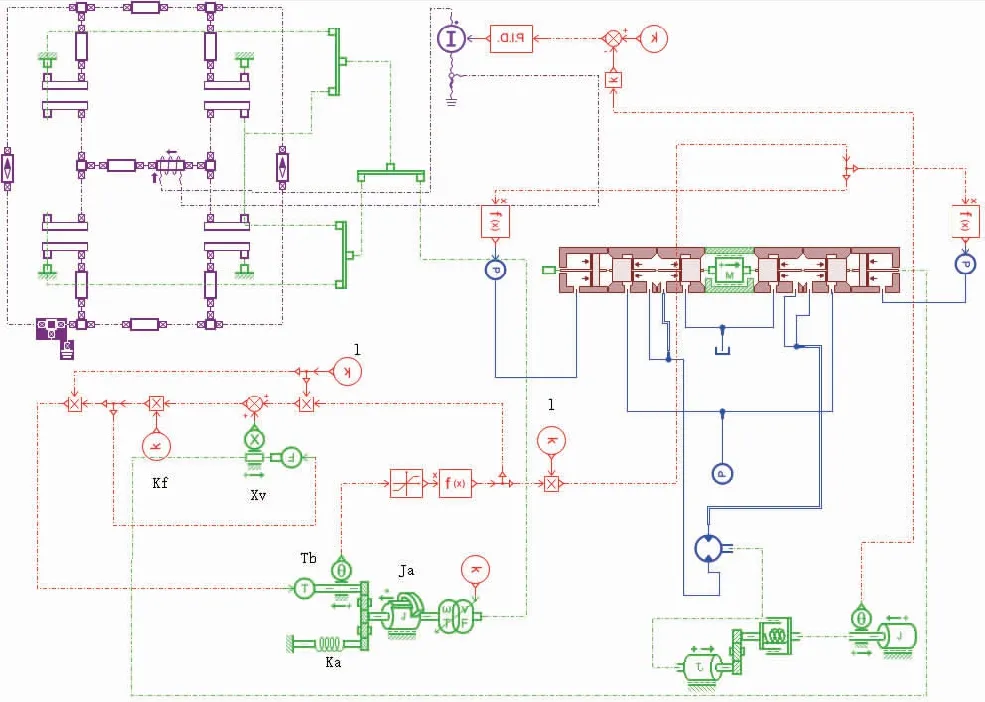
图2 射流管阀控液压马达仿真模型Fig.2 Simulation model of jet pipe valve-controlled hydraulic motor

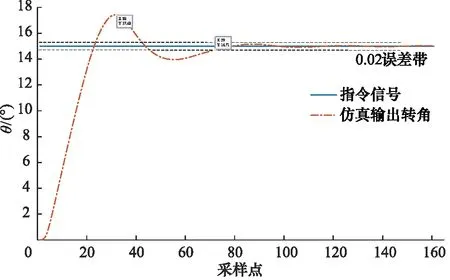
图3 辨识前输出转角仿真曲线Fig.3 Simulation curve of output Angle before identification

仅仅通过手动调整未知参数的方式,获取的仿真模型往往缺乏实证性和准确性,利用其数据进行进一步处理也将缺乏说服力,为此需进行参数辨识。

2.2 特性实验与参数辨识

在数学模型式(1)～式(9)的基础上,可以将系统开环传递函数简化为力矩马达-射流放大器放大环节、滑阀放大环节和阀控马达放大环节[11-15],对应简化后的射流管阀控液压马达的开环传递函数为:

(10)

式中,Ap—— 滑阀工作面积,Kv=KQ/Ap

Kvf—— 力矩马达开环增益

ωs—— 滑阀放大环节的液压频率,滑阀阻尼比ζs

ωh—— 阀控马达的液压频率阀控马达阻尼比ζ

当加入PID闭环反馈后,实际系统中只利用了PID控制的比例环节,对应液压马达的理论闭环传递函数为:

(11)

式中,θm0—— 输入指令角度

Kp—— PID控制的比例增益

当利用AMESim软件搭建其仿真模型时,仿真模型会与理论数学模型存在偏差,假设对应表现在闭环传递函数中的偏差为ΔG1(s),因此对应的仿真模型的传递函数可以表示为:

Gf(s)=G(s)+ΔG1(s)

(12)

此外,实际液压马达由于一些参数不确定、以及工作环境等影响因素的存在,因此与仿真模型也会存在偏差,假设这种偏差表现为传递函数的偏差为ΔG2(s),进而对应的实际液压马达的传递函数可以表示为:

Gr(s)=G(s)+ΔG1(s)+ΔG2(s)

(13)

由于Kvf、Kp、KQ、KC、Jm等参数未知,为得到准确的仿真模型,需要对这些参数进行辨识,从而得到准确的实际液压马达传递函数Gr(s),并且可以利用这些参数的不确定性来替换偏差作用,使得通过实验数据进行参数辨识后的这些参数即可带入到仿真模型当中,使得仿真模型与实际模型相契合。

进行实体平台的阶跃特性实验,利用实验数据进行参数辨识来准确化仿真模型。射流管阀液压马达实验台脱密后的结构示意图如图4所示。

图4 射流管阀控液压马达实验台示意图Fig.4 Schematic diagram of jet pipe valve-controlled hydraulic motor test bench

整个实验系统由四部分组成:上位机、工控机、控制柜和作动器。在上位机上设置偏转指令,设置两秒频率为80 Hz的采样过程,利用角度传感器采集输出转角数据。经过转换可以得到输出转角数据如图5所示。

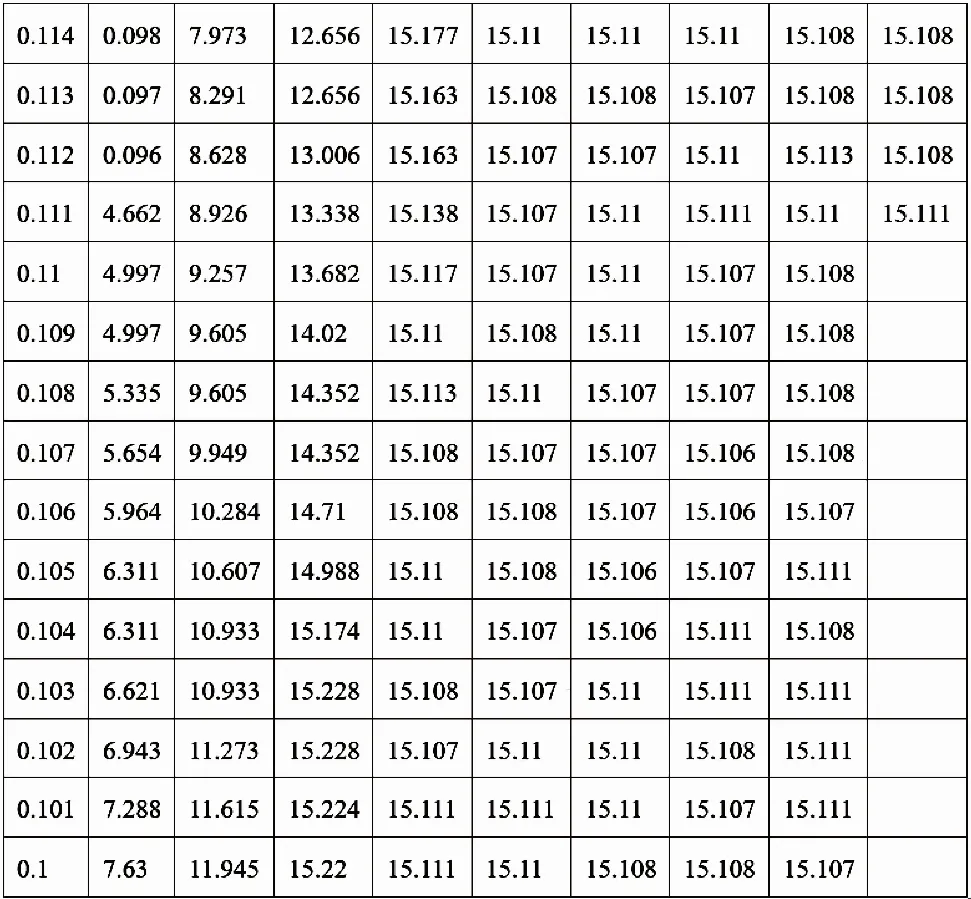
图5 采样数据Fig.5 Sampled data

将图5的实验数据利用MATLAB中的系统辨识工具箱[16],对系统的射流管阀控液压马达的传递函数Gr(s)进行参数辨识,辨识的结果为:

Kvf=999.5s-1,Kp=259.8,KQ=0.75 L/ms,KC=0.063 Lsm/kg,Jm=3.1 kgm2。

将这些参数代入仿真模型后,得到的图5采样实验数据和仿真输出转角曲线对比如图6所示。

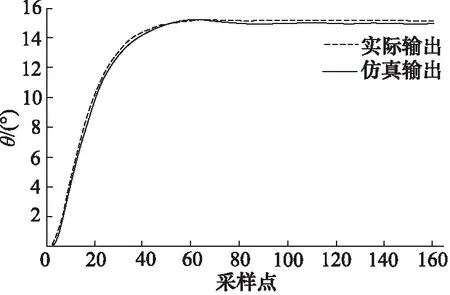
图6 实验和仿真输出转角曲线对比Fig.6 Comparison of experimental and simulation output Angle curves

参数辨识后,实验和仿真数据所对应的时域性能指标如表1所示。

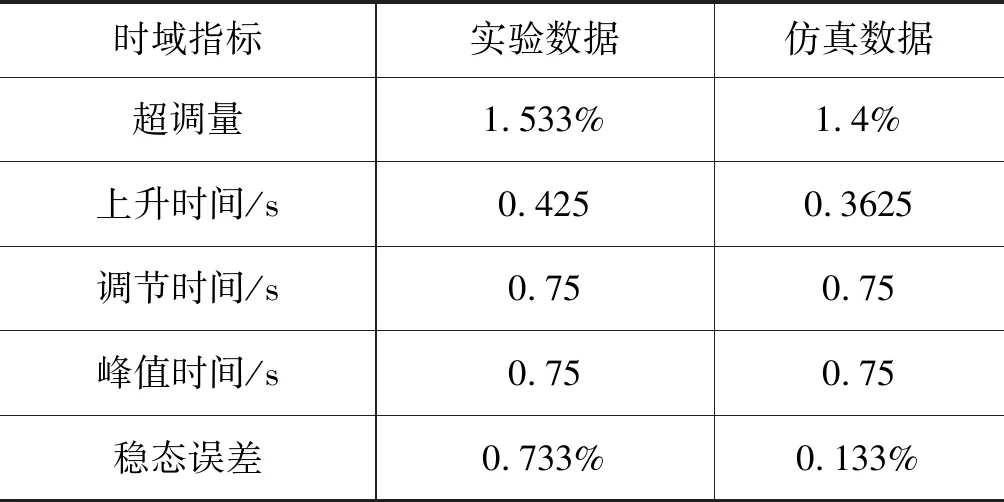
表1 实验和仿真数据的时域指标Tab.1 Time domain index of experimental and simulation data

实验验证,射流管阀控液压伺服作动器的AMESim仿真模型与实际实验台的输出转角曲线及性能指标基本一致,满足工程应用研究中的误差范围,由此验证本研究所建立的仿真模型的准确化与有效性。

3 故障诊断

在准确化仿真模型的基础上,利用BP神经网络进行基于模型的故障诊断,整体流程包括三个部分:故障选取与注入、故障样本建立以及故障诊断。

3.1 故障选取与注入

与传统的液压马达相比,射流管阀控液压马达的典型故障区别在于抗污染能力强,前导级堵塞故障概率等级低[17-18]。结合实际作动器和工程射流管阀控液压马达的故障模式进行调研分析,建立故障树如图7所示,对应的故障事件如表2所示。

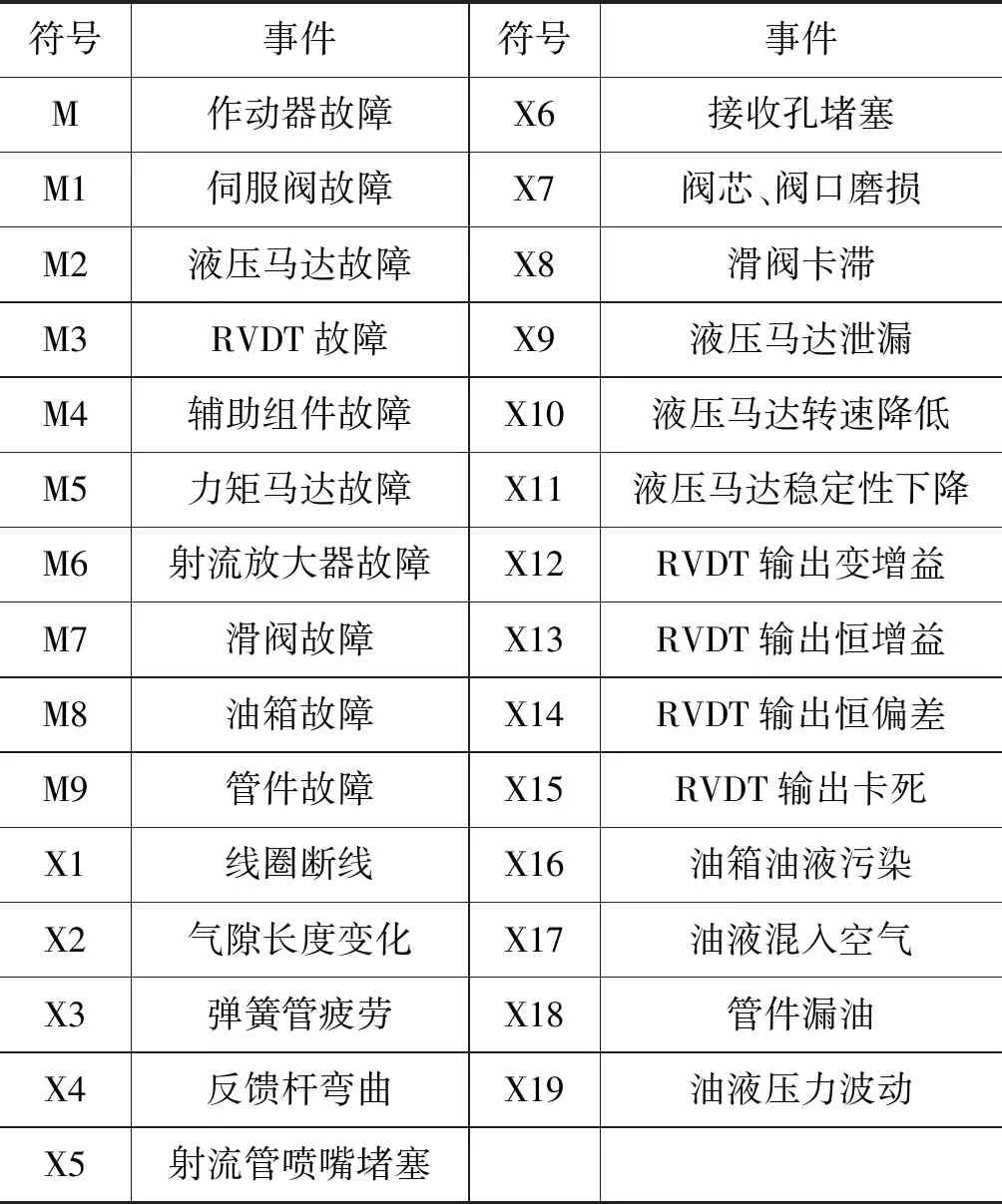
表2 故障树事件表Tab.2 Fault tree event table

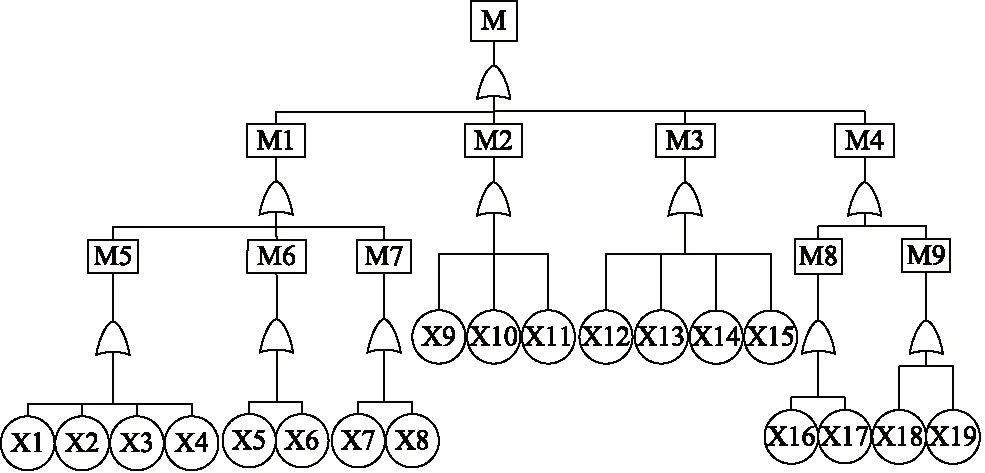
图7 射流管阀控液压马达故障树Fig.7 Jet pipe valve controlhydraulic motor fault tree

根据因素水平表和FMEA表选取故障概率较高和严酷度较严重的几个故障为:气隙长度变化、滑阀圆角磨损、滑阀外泄漏(管件漏油导致)、滑阀卡滞、液压马达内泄漏、角位移传感器常值漂移、油液混入空气、油液污染、油液压力波动。

结合工程实际经验和实体液压马达调研,实际作动器平台的角位移传感器是多余度的可靠性很高,并且油液除污和除气装置有多级,因此不考虑传感器、油液混入空气和油液污染等故障。因此,确定最终需要进行检测和诊断的典型故障模式为:气隙长度变化、液压马达内泄漏、油液压力波动、滑阀卡滞、滑阀圆角磨损、滑阀外泄漏等六个典型故障。

将典型故障注入到准确化后的射流管阀控液压马达仿真模型当中,各故障仿真方法如图8和表3所示,通过参数修改和模型微调的方式来实现故障模拟注入。将各典型故障的相关参数进行批处理,设置15种不同程度的故障,通过仿真得到各故障仿真原始数据。利用参数不确定性来取代实际作动器的非线性和不确定性,从而可替代实际数据作为原始数据进行故障诊断。

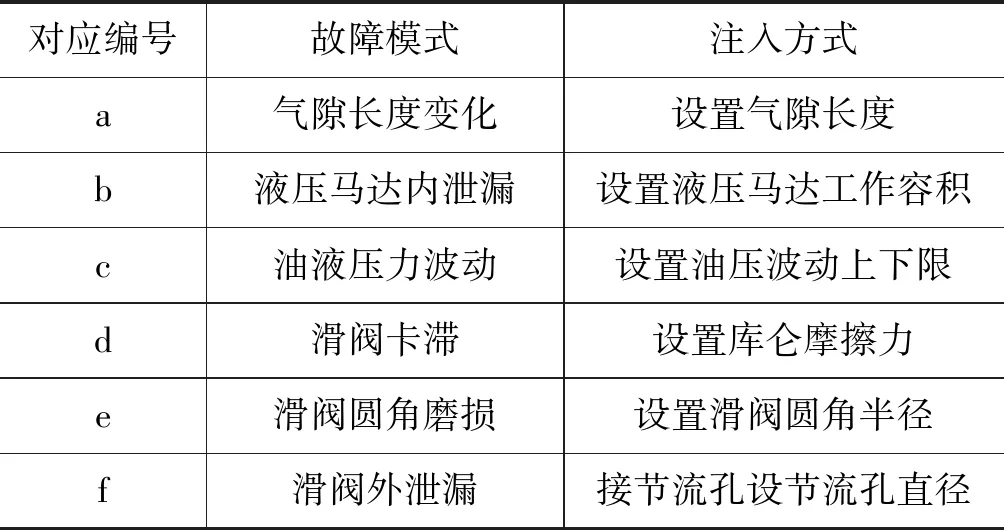
表3 故障注入方法Tab.3 Fault injection method

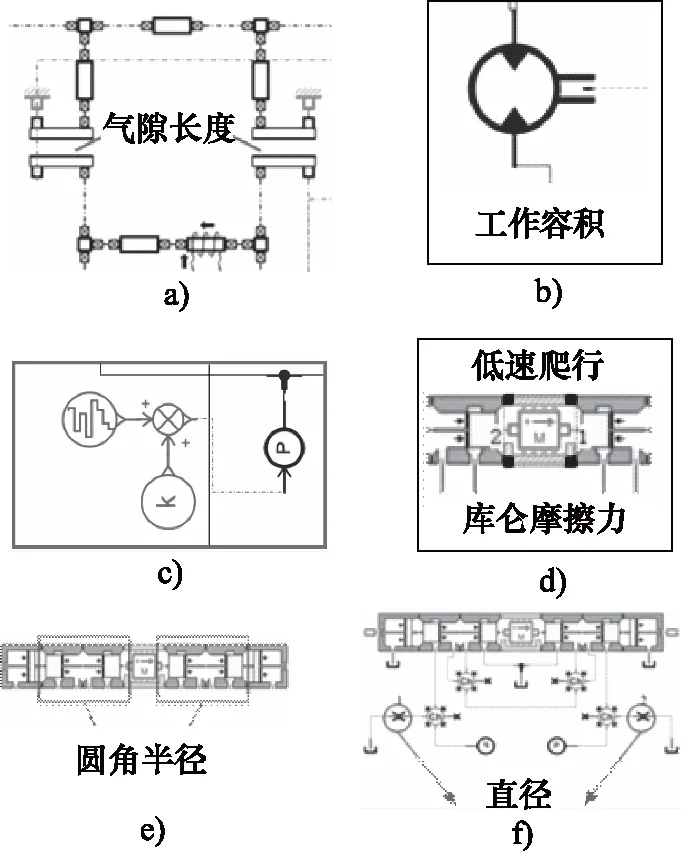
图8 故障注入位置及需要调整的参数Fig.8 Fault injection position and parameters to be adjusted

3.2 数据预处理与故障样本建立

对获取到的原始数据进行数据预处理,利用MATLAB提取故障特征,利用特征量来描述当前系统的状态,作为元素建立故障样本。由于本研究的液压系统固有频率较低,因此提取时域特征能够很好地在故障诊断中描述系统真实且全面的状态。根据仿真结果,选取了15种故障特征来刻画不同故障参数与故障模式对系统性能的影响:最大值、均值、有效值、峰值因子、波形因子、脉冲因子、裕度因子、中位数、方差、标准差、峭度、偏度、上升时间、末时刻位移、误差。

为研究参数值设置与特征量的相关性,利用相关性函数Pearson实现特征量与参数值的拟合,从而计算两者的相关性数值。计算典型故障F1～F6的参数设置与原15种故障特征的Pearson相关系数,并绘制如图9所示的热图,色调越接近黄色相关性越好,相反越接近绿色相关性越差。

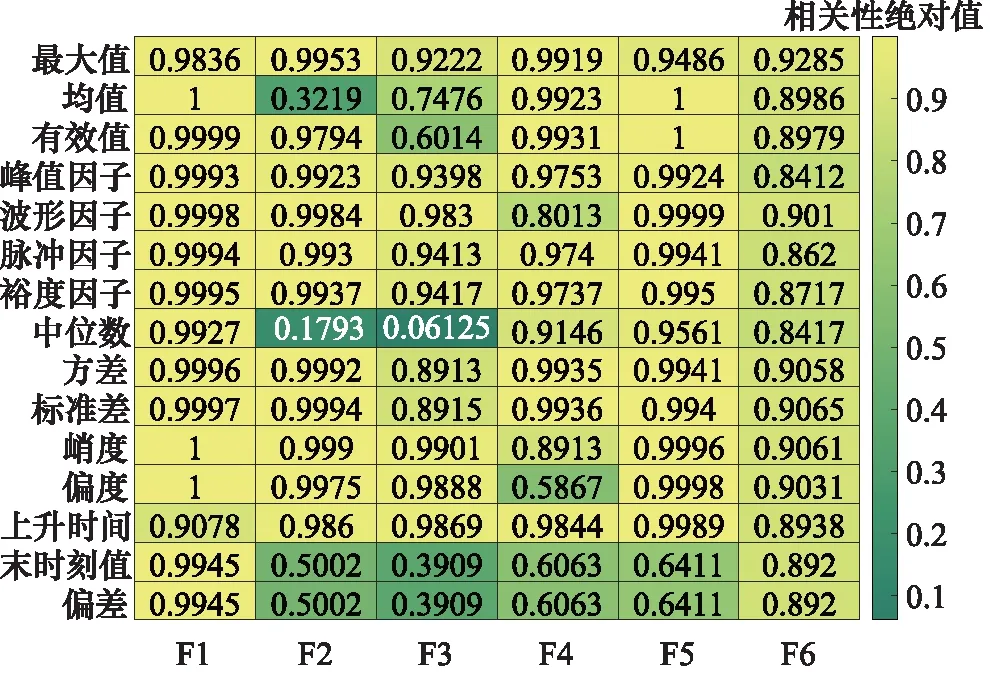
图9 故障参数与特征量相关性热图Fig.9 Heat map of correlation between fault parameters and characteristic quantities

从图9可以看出6种故障模式下,特征量:中位数、末时刻值和偏差与参数设置的相关系数最低,即相关性最差。与此同时,在观察各故障输出曲线时发现,这三种特征量仅表示一个时刻的值或与指令的误差,难以反映整个曲线的信息。

为此提取剩余12种故障特征作为故障样本,由于六种典型故障每15种不同程度注入到仿真模型,对应有6×15组原始数据。提取故障特征作为样本,因此总共有90组故障样本,利用系统抽样确定1-15中的数字为10,因此确定编号为10,25,40,55,70,85等六组样本作为验证样本,剩余84组作为训练样本。

3.3 基于BP神经网络故障诊断

对获取到的样本数据利用BP神经网络进行故障诊断,BP神经网络采用多层网络使得所需训练的非线性数据的输入与输出逼近。目的是通过神经网络训练来找到样本向量和故障模式之间的函数映射[19],首先对故障模式进行编码,如表4所示,后续利用编号F1-F6来简化并指代典型故障。

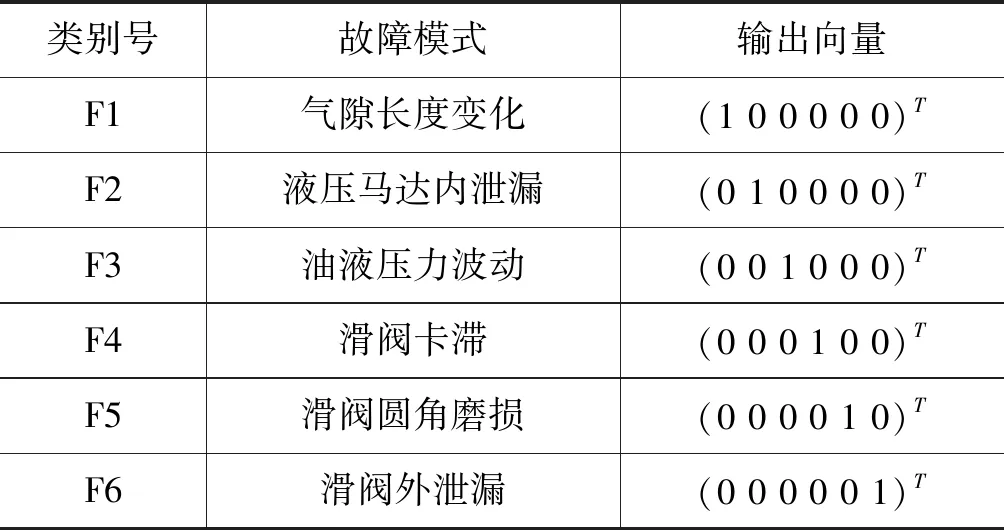
表4 故障模式输出向量编码Tab.4 Output vector encoding of fault mode

利用MATLAB软件进行编程,设置神经网络结构参数,进行神经网络学习和训练,发现当隐含层神经元个数为40,学习率为0.001时,神经网络的诊断性能最佳,训练时间为3 s,神经网络训练结果如图10所示。

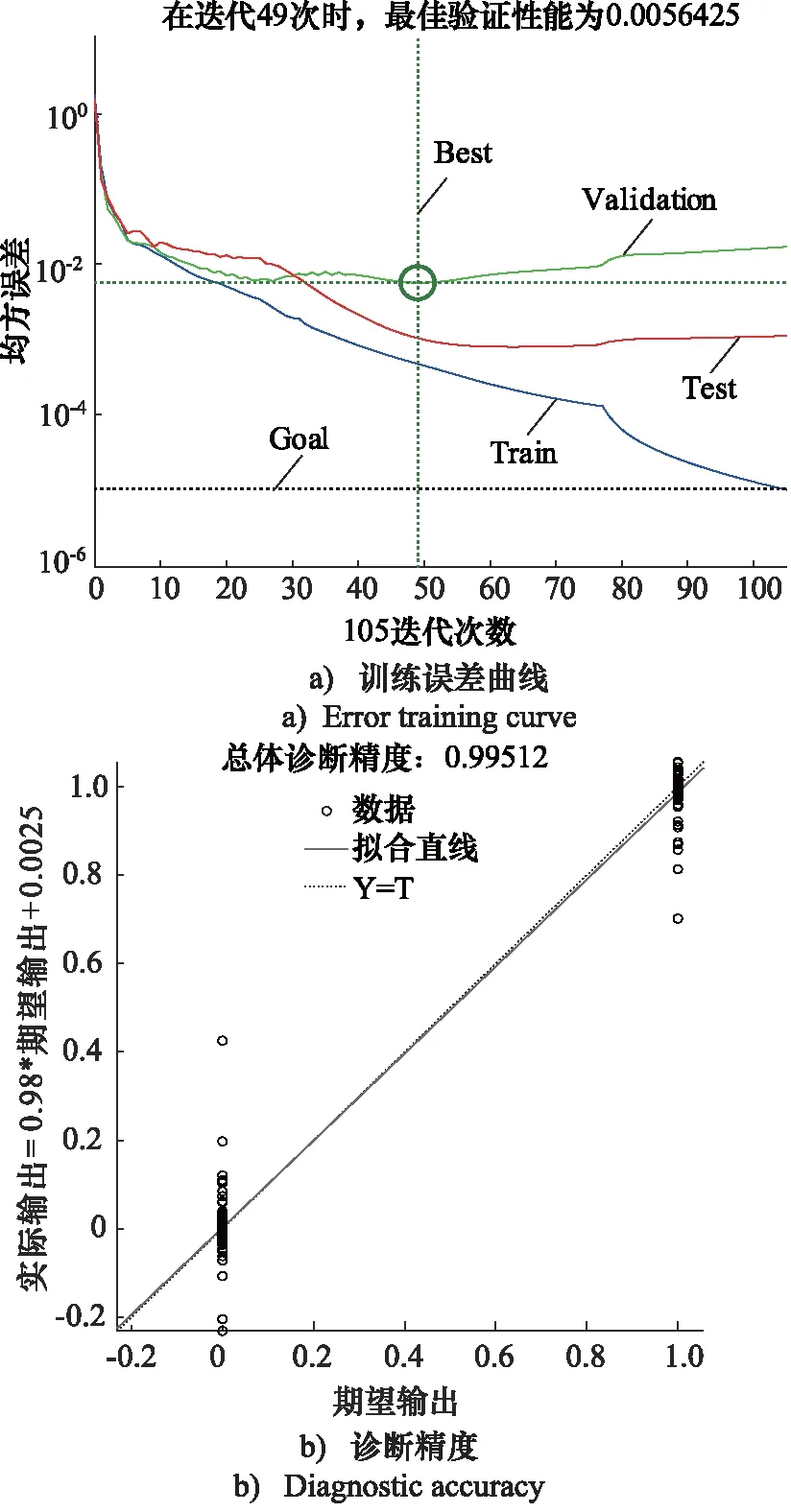
图10 特征量选择优化神经网络训练结果Fig.10 Eigenvalue selection optimization neural network training results

将测试样本导入训练好的神经网络中进行测试验证,得到的测试结果如表5所示。

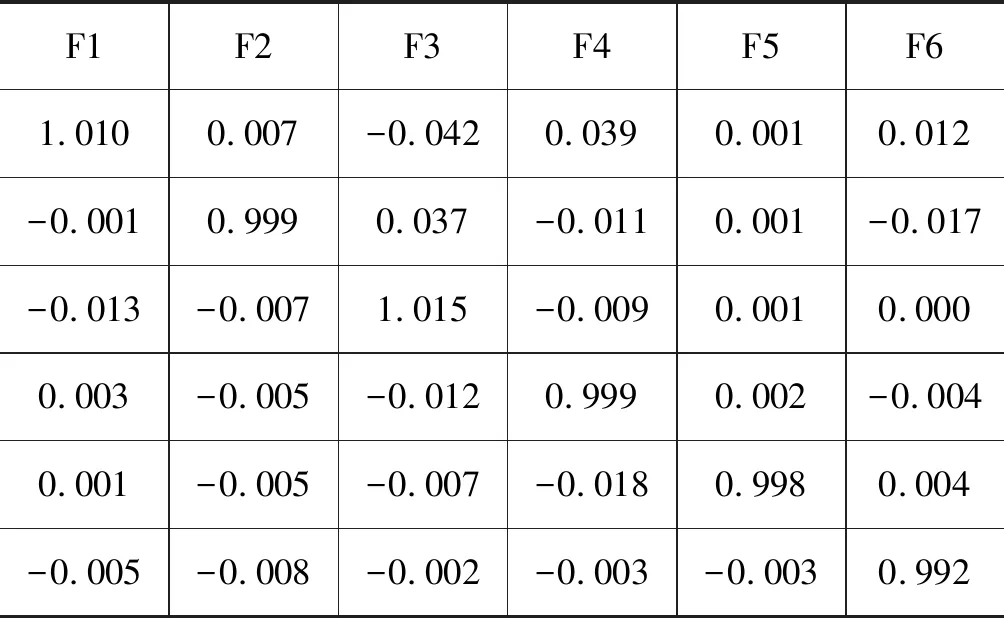
表5 特征量选择优化诊断测试结果Tab.5 Feature selection optimizes diagnostic test results

从图10a中可以看出,当迭代105次后,神经网络的训练误差低于1e-5,满足要求,从图10b中可以看出,本次训练的诊断精度达到了99.512%。将表5的测试结果与单一故障编码输出向量表对比,可知特征选择优化后的故障诊断方法对典型故障F1～F6完成了准确的故障诊断,平均误差为0.00895。

4 结论

本研究对射流管阀控液压伺服作动器液压马达进行了模型建立以及实验数据拟合,对实验数据进行了关键特征量的分析与提取,并预处理采样数据;利用较为成熟的BP神经网络实现了有效准确的故障诊断。

(1) 利用AMESim软件搭建了射流管阀控液压伺服作动器的仿真模型,并且利用实体阶跃特性实验进行参数辨识,对其进行参数准确化,使得仿真与实验输出曲线的时域性能指标包括上升时间、峰值时间、超调量、调节时间、稳态误差基本一致,从而验证仿真模型的准确性与有效性;

(2) 通过仿真模型获取仿真原始数据,通过计算故障参数设置与特征量的Pearson相关性系数,选取能够准确描述系统整体性能的12种特征量作为故障样本,利用BP神经网络对其进行训练,结合验证样本验证训练好的神经网络,结果显示能够对系统的典型故障进行准确率高达99.512%的故障诊断。