矿井提升机电液制动非线性控制方法

汤 裕, 解 辉, 沈 刚, 朱真才, 李 翔

(1.中国矿业大学 机电工程学院, 江苏 徐州 221000;2.安徽理工大学 机械工程学院, 安徽 淮南 232000)

引言

矿井提升机是煤炭生产系统中的关键装备,主要用于提升原煤、人员、设备等,直接影响着煤矿生产的效率及安全性[1],而制动装置作为矿井提升机最后一道安全保障设备,其对提升机的安全运行起着至关重要的作用。然而,钢丝绳作为提升系统的关键部件,由于其弹性特性导致提升系统在制动过程中表现出极其复杂的动态特性,例如提升容器的振动和冲击现象,甚至出现过卷、失速和钢丝绳断裂等严重事故[2]。因此,合理可靠的制动控制方法是保障提升系统安全运行的关键。

现有的提升机制动控制策略主要包括恒力矩制动和恒减速制动[3]。与开环的恒力矩制动相比,恒减速制动可以利用卷筒转角的反馈信息实时调整制动力矩,使得卷筒按照期望减速曲线运行。由于恒减速制动控制具有冲击小、安全性高、动态性能好等优点,在提升机制动控制中得到了广泛应用。相关研究人员在恒减速制动的基础上,进一步采用神经网络算法[4]、遗传算法[5]等方法以提升制动控制性能。然而,目前恒减速制动控制策略大多忽略了提升钢丝绳的弹性特性,从而限制了制动控制性能的进一步提高。因此,有必要采用基于系统模型的非线性控制策略来改善制动性能。

目前,矿井提升系统作为典型的弹性传动系统,其建模方法主要分为两类:使用集中参数的离散模型[6]和使用分布参数的连续模型[7]。与离散模型相比,连续模型能较好地描述钢丝绳连续特性,在提升系统建模和动态特性分析中得到了广泛的应用,例如ZHU Zhencai等[8]考虑提升钢丝绳的柔性特性,利用拉格朗日第二类建立了双绳缠绕式提升系统动力学模型,并通过合理选择系统状态变量将动力学模型转化为具有严格反馈形式的状态方程形式,进而满足非线性钢丝绳张力协调控制器的设计要求。

由于矿井提升机运行中存在着由钢丝绳刚度和阻尼等参数不确定性产生时变扰动,以及由罐道摩擦和提升容器横摆而造成的机械动力学不确定性,这些不利极大影响制动控制性能。为解决运行过程类似的不确定性扰动,研究人员在相近的领域提出了一些解决方法,如高增益扰动观测器[9-10]、带扰动观测器的滑模控制[11-12]、自适应扩展扰动观测器[13]等。然而,上述控制方法大多需要被控系统精确的动力学模型,并且在方法的设计过程中需要跟踪误差的高阶求导,在这一过程中可能存在微分爆炸问题[14],导致控制方法无法实现。近年来,神经网络技术因其在识别动态不确定性方面的潜在优势而受到广泛关注[15],例如GUO Q等[16]针对液压参数不确定和外部负载未知的集总条件下液压缸位置的动态跟踪控制问题,提出了一种电液系统神经网络自适应控制器,并引入自适应估计律来调整权重向量,以增强神经控制器的鲁棒性。

受上述研究的启发,针对具有建模不确定性与外部不确定扰动的矿井提升机制动控制问题,提出了一种基于系统模型的电液制动非线性控制方法,利用李雅普诺夫稳定性分析理论证明了闭环系统的稳定性。本研究的主要贡献如下:

(1) 建立了单绳缠绕式矿井提升机制动控制模型,提出了基于模型的矿井提升机制动控制策略。与无模型控制策略相比,所提出方法考虑了提升系统的非线性特性;

(2) 针对系统存在的建模不确定性与外部不确定性扰动,利用神经网络对不确定性进行了估计和补偿,并构造了自适应权值估计律,增强了控制的鲁棒性,且不需要预先规定未知外部扰动的边界;

(3) 利用神经网络函数对不确定性和虚拟控制律进行了合并逼近,从而避免了传统控制方法设计过程中需要对跟踪误差进行高阶求导导致的微分爆炸问题,提高了控制的鲁棒性。

1 矿井提升机系统建模

单绳缠绕式矿井提升机系统结构示意如图1所示,其中图1a给出了提升系统的结构构成,图1b给出了提升系统的几何关系和部件的参数定义。

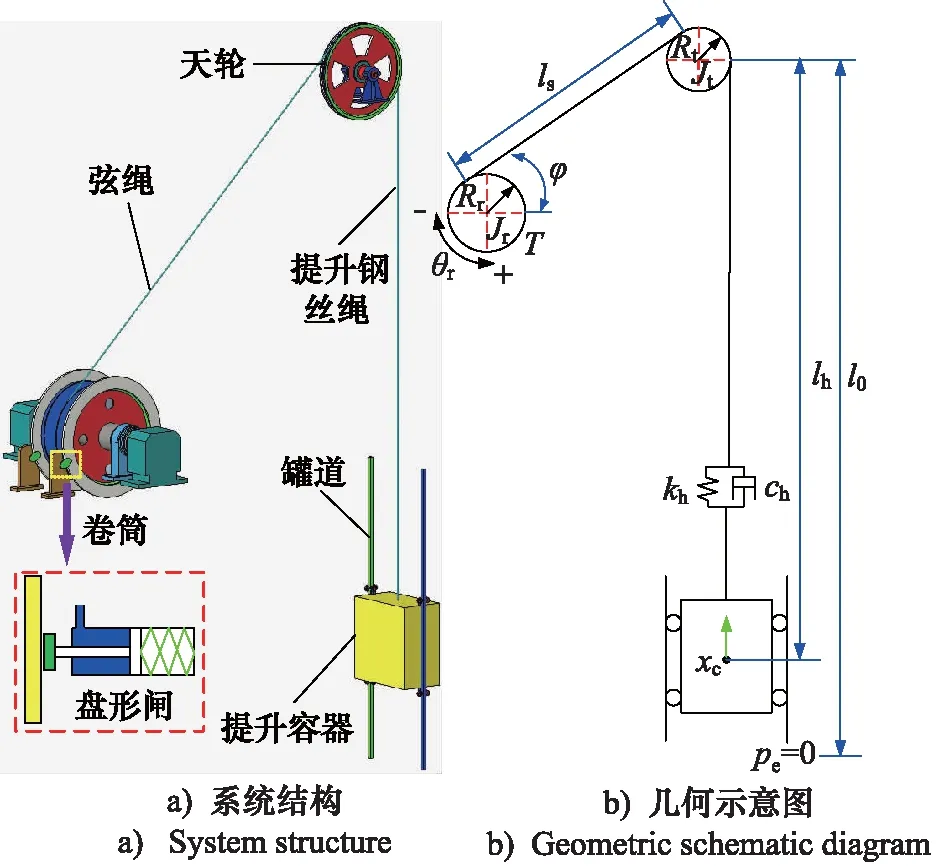
图1 单绳缠绕式矿井提升机系统Fig.1 Single rope winding mine hoist system

定义提升机的提升方向为正向,提升钢丝绳的长度为:

lh=l0-Rrθr

(1)

其中,l0为提升钢丝绳的初始长度;Rr为卷筒的缠绕半径;θr为卷筒的转动角度。

为了简化建模,本研究忽略了提升机的横向与纵向振动,定义提升系统广义坐标为q=[xc,θr]T,xc是提升容器的纵向位移。提升系统的动力学模型依据拉格朗日动力学方程建立:

(2)

其中,T,U,D,Q分别为提升机的动能、势能、瑞丽耗散函数和非有势力向量。下一步将式(2)中所涉及的能量进行计算,提升容器动能T表示如下:

T=Tls+Tlh+Tr+Tt+Tc

(3)

其中,Tls,Tlh,Tr,Tt,Tc分别为提升钢丝绳、弦绳、卷筒、天轮和提升容器的动能;pl是单位长度钢丝绳的质量;Ir和It分别是卷筒和天轮转动惯量;Rr和Rt分别是卷筒和天轮转动半径;m是提升容器质量;

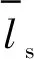
(4)

(5)

提升系统的势能表示如下:

(6)

其中,Uls,Ulh和Uc分别为弦绳,提升钢丝绳和提升容器重力势能;Uk是钢丝的弹性势能;kh是钢丝绳的刚度;φ是弦绳与提升钢丝之间的夹角。

提升系统的瑞丽耗散函数表示为:

(7)

其中,ch是钢丝绳的阻尼比。考虑提升系统制动过程中存在的罐道摩擦、卷筒转动摩擦以及缠绕误差等因素,结合式(2)～式(7),提升系统的动力学模型为:

khRrθr+mcg=Fd

(8)

=Tz+Td

(9)

其中,Tz为作用在闸盘上的制动力矩;Fd和Td是钢丝绳与罐道之间的摩擦、卷筒与天轮的卷绕波动和主轴摩擦等引起的外部不确定性扰动;d(t)是由钢丝绳刚度阻尼、卷筒和天轮尺寸等变化引起的时变扰动。

(10)

其中,θ1=-ch/(2ρll0/3+m),

θ2=-kh/(2ρll0/3+m),

θ3=chRr/(2ρll0/3+m),

a1=(khRrθr-mg)/(2ρll0/3+m),

d1=Fd/(2ρll0/3+m),

θ6=chRr/A,θ7=khRr/A,

θ8=1/A,d2=[Td-d(t)]/A,

0.5ρlgRrl0)/A,

2 非线性制动控制器设计

针对矿井提升机制动模型式(10)中存在的建模误差以及外部扰动,考虑到神经网络具有估计任意未知动态扰动的能力,设计一个神经自适应网络控制器来估计和补偿提升机制动控制模型中的不确定项与外部时变扰动d1和d2。在控制器设计之前,有以下假设:

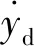
本研究中利用径向基神经网络估计连续未知函数Fi(X),结构如下:

(11)

其中,X是输入向量;Wi∈RN是权值向量;N是径向基神经网络的核心数;φi(X)=[u1,u2,…,uN]T表示高斯函数向量;δi(X)表示径向基神经网络估计误差且满足|δi(X)|<δmax,i=1,2,…,n,其中δmax表示未知界。

向量φi(X)的径向基元uj设计如下:

(12)

其中,cj和σj分别是高斯函数第j个节点的中心和宽度参数;σj为大于0的数,它决定径向基函数的围绕中心点的宽度。

定义提升机制动控制系统状态跟踪误差e=[e1,e2,e3]T,结构如下:

(13)

其中,x1d=yd表示期望制动轨迹;α1和α2表示虚拟控制输入。

步骤1:根据式(10)和式(13),位置跟踪误差e1关于时间的导数为:

(14)

为使状态跟踪误差e1收敛至0,定义一个半正定的李雅普诺夫函数V0如下:

(15)

利用式(14),对式(15)进行求导得到:

(16)

根据式(16),虚拟控制输入α1设计为:

(17)

其中:k1是一个大于0的反馈调节增益,将式(17)代入式(16),V0关于时间的导数可以推导为:

(18)

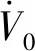
步骤2:结合式(10)和式(17),状态跟踪误差e2关于时间的导数为:

(19)

为确保跟踪误差e2的收敛性,定义半正定李雅普诺夫函数V1为:

(20)

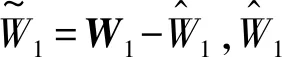
结合式(19)和式(20),V1关于时间的导数为:

(21)

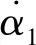
(22)

将式(22)代入式(21),得到:

(23)

根据式(23),虚拟控制输入α2和权值向量W1自适应律设计为:

(24)

(25)

其中,k2是大于0的反馈调节增益;η1用于增强神经网络控制器鲁棒性的自适应调节参数。将式(24)和(25)代入式(23)得到:

(26)

步骤3:对状态跟踪误差e3进行求导,得到:

(27)

类似步骤2,定义李雅普诺夫函数V2为:

(28)

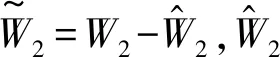
结合式(27)和式(28),V2关于时间的导数为:

(29)

(30)

将式(30)代入到式(29)得到:

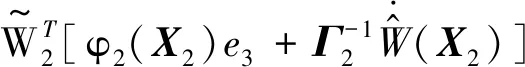
(31)

因此,根据式(31),最终的控制输入Tz与权值向量自适应律W2设计为:

(32)

(33)

其中,k3是大于0反馈调节增益,η2是大于0常数。将式(32)和式(33)代入式(31)得到:

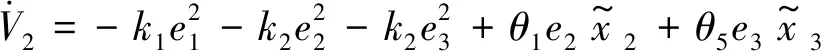
e3δ2(X2)

(34)

步骤4:制动系统的是通过盘形制动器内部的簧片推动闸瓦用于卷筒上的闸盘产正压力,进而获得制动扭矩,而式(31)中的制动扭矩不能直接用于实际应用。因此,下一步的工作是根据所需的制动扭矩获得制动力。通常,制动力和扭矩之间的关系描述如下[17]:

(35)

其中,Fz是制动力;Rz是制动半径;nz制动器数量;fz是制动摩擦系数。

3 非线性制动控制器稳定性分析

为了证明设计非线性制动控制器的稳定性,定义整个闭环系统的李雅普诺夫函数V如下:

(36)

对V进行求导,得到:

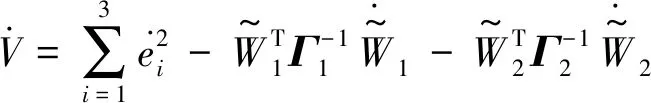
e2δ1(X1)-e3δ2(X2)

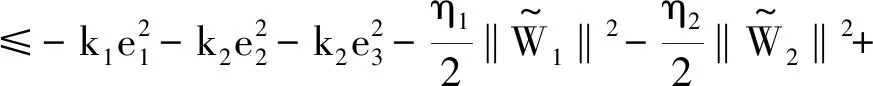
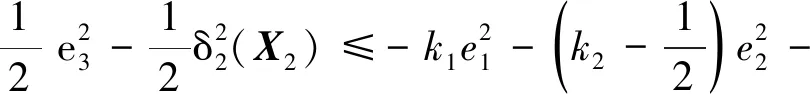
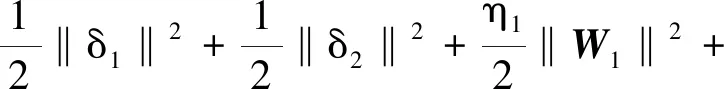
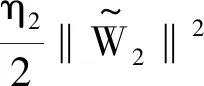
(37)

定义一个常数φ*为:

(38)

其中,λmax(·)是矩阵的最大特征值,将式(37)代入式(36)改写为:

(39)

其中,

(40)

将式(39)两端求导,得到:

(41)

4 非线性制动控制器实验验证

为了验证提出的非线性制动控制器的有效性和优越性,建立了如图2所示的单绳缠绕式矿井提升机模拟实验台。实验台包括基于MATLAB/Simulink的实时控制系统、提升绳、提升容器、柔性导向、四个带制动盘的液压缸、卷筒、液压马达、天轮、液压泵站。液压缸用于制动系统的制动力控制,制动液压缸安装有力传感器,实时测量制动压力。通过在卷筒上施加制动力矩,实现卷筒的速度控制,进而控制提升容器的位置。除此之外,实验台提升系统配备了位移传感器以实时测量提升容器的位置。单绳缠绕式矿井提升机模拟实验台主要参数见表1。

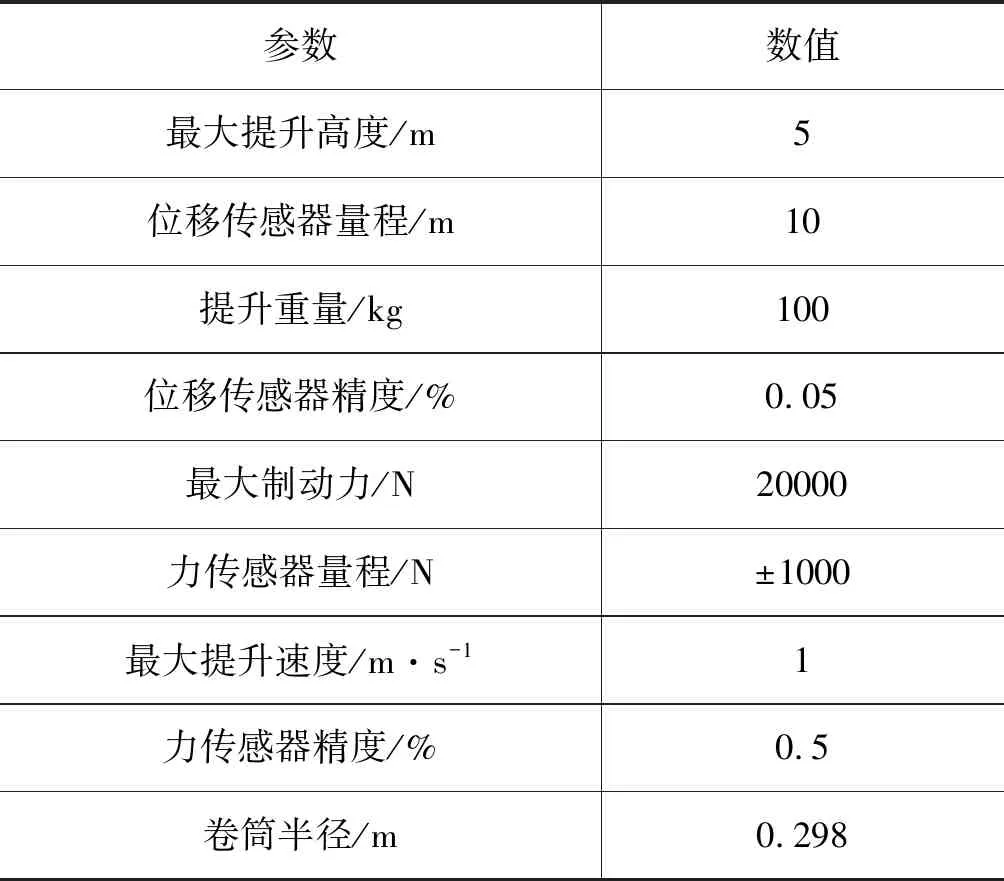
表1 实验台关键参数Tab.1 Main parameters of test bench

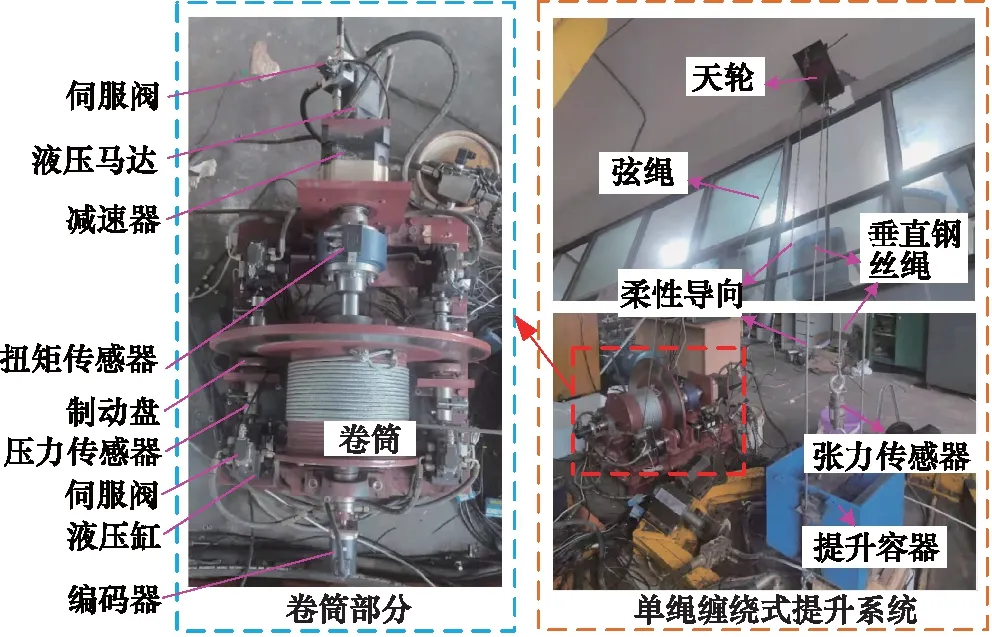
图2 单绳缠绕式矿井提升机模拟实验台Fig.2 Single rope winding mine hoist system test bench

为了验证提出的非线性控制器的有效性和可行性,采用液压马达作为卷筒的驱动,在制动开始时将液压马达的进油腔与回油腔连接,此时驱动扭矩突然降至零以模拟紧急制动工况,即卷筒仅受制动扭矩的作用。除本研究所设计的控制器,另外选择PI控制器和反步控制器作为对照实验。

(1) 提出控制器:本研究的采用自适应神经网络的非线性控制器,实验中利用试错法得到的控制器参数为:k1=2×103,k2=1.1×103,k3=0.3×103,η1=0.01,η2=0.03,σ1=11,σ2=11,Γ1={8,8,8,8,8,8,8,8,8,8,8},Γ2={5,5,5,5,5,5,5,5,5,5,5},c1={-5,-2,1,4,7,10,13,16,19,22,25},X1∈[-5,15],c2={-30,-24,-18,-12,-6,0,6,12,18,24,30},X2∈[-30,30]。

(2) 反步控制器:未考虑系统存在的建模不确定性以及外部扰动,基于矿井提升机制动控制模型,利用反步法设计得到的非线性控制器。为了公平比较,反步控制器的控制器参数设置与提出控制器中对应参数相同。

(3) PID控制器:工业中广泛应用的传统比例-积分-微分控制器。控制器参数选择为:kp=1.3×104,ki=0.8×103,kd=0,其中:kp,ki,kd分别为比例增益、积分增益、微分增益。

对比实验中提升容器运行速度参考信号如图3所示,在09 s阶段,提升机实验台处于停车状态。

图3 提升容器运行速度参考信号Fig.3 Reference signal of mine hoist conveyance

如图4所示为采用PID控制器后的实验结果。从图可以看出,在制动和停车的开始阶段,位置和速度偏差较大,并呈现出明显的阻尼振荡现象,这在图4b中的速度曲线表现尤为明显;在9 s时,提升机在停车开始时明显抖动,此时跟踪误差增大,制动力增大、卷筒抱死,而提升容器仍然有一定的速度,所以发生明显的振荡现象。造成以上现象的原因是由于PID控制器忽略了钢丝绳的弹性特性,仅利用位置跟踪误差来调节制动力,所以难以获得较高的制动性能。

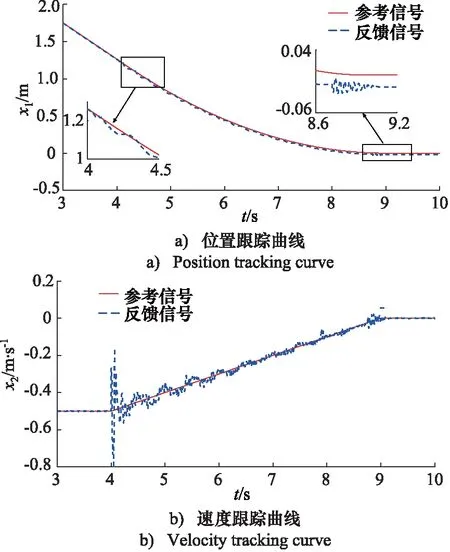
图4 PID控制器实验结果Fig.4 Experimental results of PID controller

图5给出了反步控制器所取得的实验结果。与PI控制器相比,反步控制器具有更好的位置跟踪精度和更低的阻尼振荡,这是由于反步控制器是一种基于系统模型的非线性控制,设计过程中考虑了提升系统的非线性特性。然而,反步控制器没有考虑建模误差和外部干扰问题,从图5b可以很容易地观察到制动过程中出现了明显的速度波动。此外,从参考信号可以看出在制动和停车的起始点,不满足Lipschitz条件,因此,反步控制器存在微分爆炸问题,从而导致制动初始阶段提升容器的震荡现象。

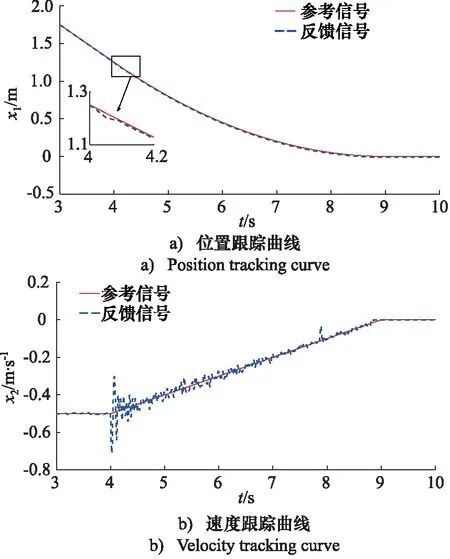
图5 反步控制器实验结果Fig.5 Experimental results of backstepping controller

提出控制器的实验结果如图6所示。为了进一步有效比较提出控制方法的有效性,图7给出了不同控制器下的实验跟踪误差曲线,图8给出了不同控制器下提升容器纵向加速度振动曲线。与此同时,为更好地定量比较不同控制器的制动控制实验效果,表2和表3分别给出了不同控制器下提升机位置跟踪误差指标和提升容器纵向加速度振动指标。

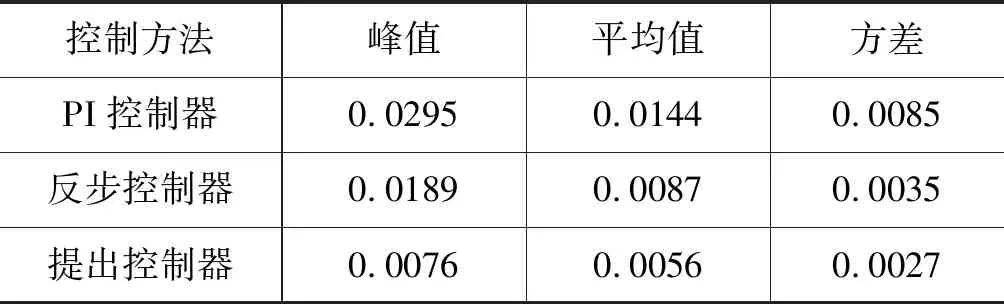
表2 不同控制器下位置跟踪误差指标Tab.2 Position tracking error index with different controllers

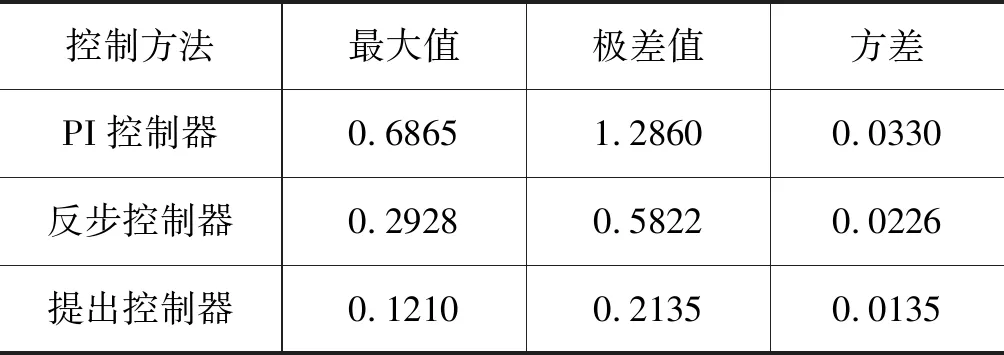
表3 不同控制器下提升容器纵向加速度指标Tab.3 Conveyance longitudinal acceleration index with different controllers

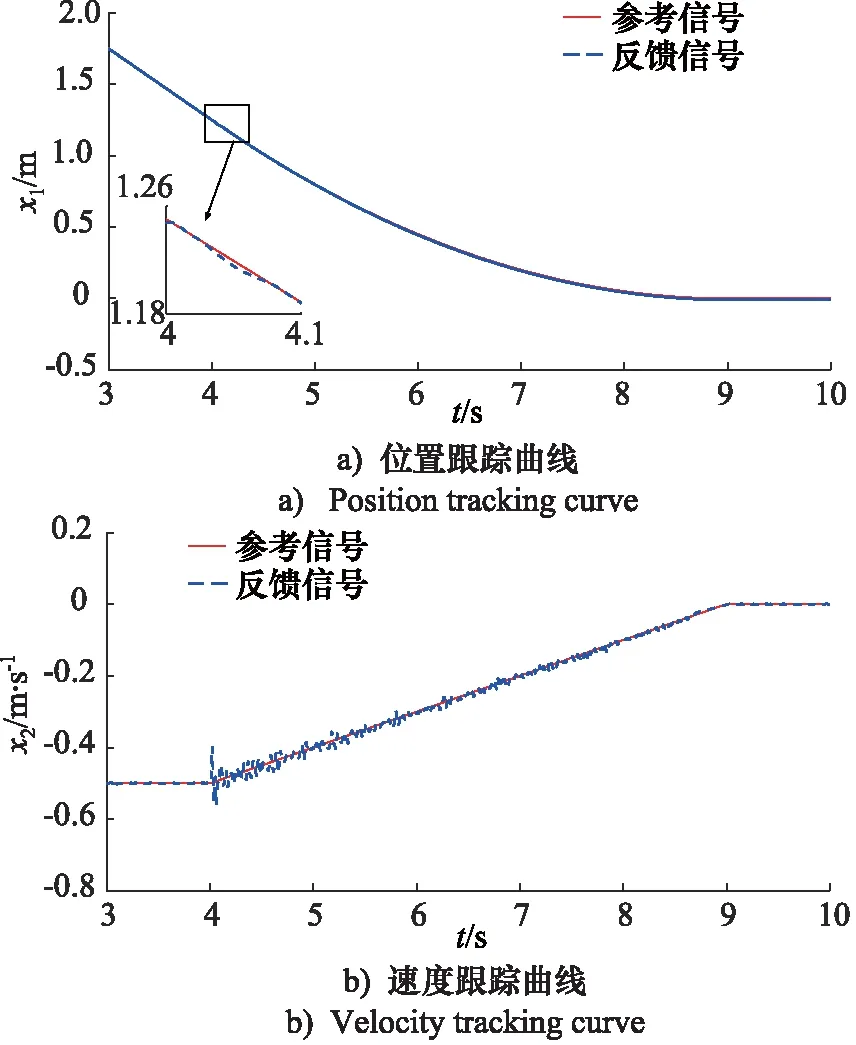
图6 提出控制器实验结果Fig.6 Experimental results of proposed controller

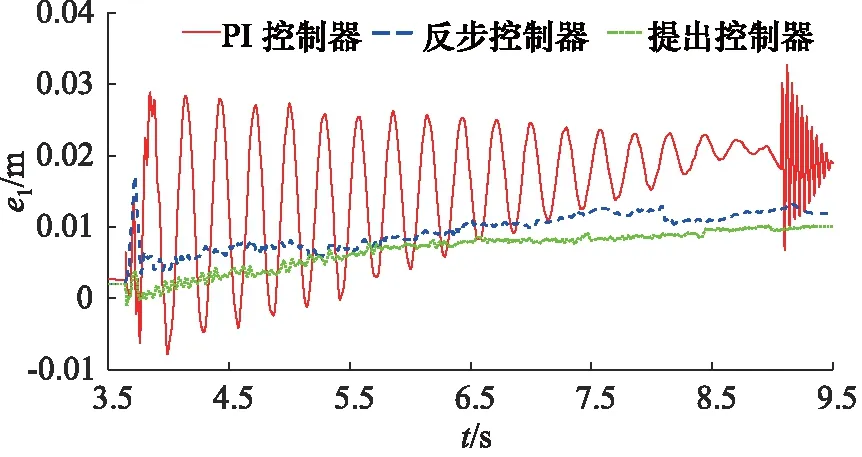
图7 不同控制器下位置跟踪误差Fig.7 Position tracking error with different controllers

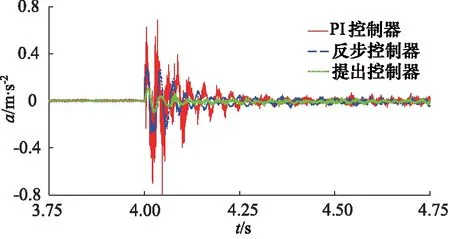
图8 不同控制器下提升容器纵向加速度曲线Fig.8 Experimental curves of longitudinal acceleration of conveyance with different controllers

从图6～图8和表2～表3中的实验结果可以看出,相较于PI控制器和反步控制器, 本研究所提出非线性控制器获得了最佳的控制性能。这是由于该非线性控制器在传统反步控制器的基础上引入了径向基神经网络单元来动态估计和补偿建模误差和外部不确定力扰动,从而解决了建模误差和外部不确定扰动问题。与此同时,从图9中不同控制器下制动力曲线可以看出,提出控制器在一定程度上解决了反步控制器中存在的微分爆炸问题。

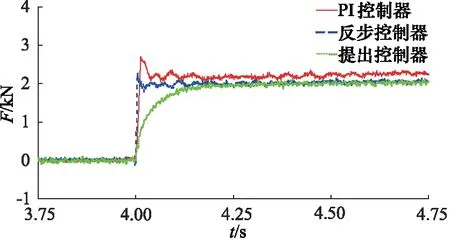
图9 不同控制器下的制动力曲线Fig.9 Braking pressure curves with different controllers

5 结论

针对矿井提升机安全平稳制动控制问题,提出了一种基于模型的矿井提升机电液制动非线性制动控制方法。该方法在传统反步设计过程中引入径向基神经网络,有效解决了建模误差和外部不确定扰动等问题,同时采用自适应更新律对神经元权值进行在线调节,增强了设计制动控制方法的鲁棒性,并且避免了由于稳定函数求导导致的微分爆炸问题。此外,通过李雅普诺夫稳定性理论证明了提出的矿井提升机非线性制动控制方法的闭环全局稳定性。最后,在搭建的单绳缠绕式矿井提升机模拟实验台上进行了对比实验,实验结果表明提出的非线性制动控制方法与传统PI控制器、反步控制器相比,在矿井提升机制动平稳性和安全性方面具有更优的制动控制效果。