基于优化模糊自适应PID的除雪撒盐车马达恒转速调控

沈建军, 唐 正, 王斌强, 贾 峰

(长安大学 道路施工技术与装备教育部重点实验室, 陕西 西安 710064)

引言

除雪撒盐车作业过程中,由于启停和转弯等情况,容易导致车辆运行不稳定,产生液压冲击,造成马达转速波动,为保证液压马达转速稳定,除雪撒盐车正常工作,需要对液压马达转速进行控制[1]。

阀控马达电液伺服系统是一种复杂的非线性时变系统,由于液压油特性及设备的制造精度等难以精确把控, 难以建立精确的数学模型。模糊自适应PID控制是基于传统PID控制方法,将专家经验与模糊数学理论结合形成的智能控制方法,具有很强的鲁棒性,且不需要精确的数学模型[2]。因此,将模糊自适应PID控制应用到复杂系统可以实现良好的控制效果。

目前许多学者使用优化算法对模糊自适应PID控制器进行优化,提高了控制效果。乔林等[3]利用遗传算法优化模糊规则和隶属度函数,结果表明具有较快的响应速度快和较强的鲁棒性;贾蒙蒙等[4]利用粒子群算法优化模糊规则和隶属度函数,提高了PID控制器的稳态性能和动态特性;汪谦松等[5]利用改进的人群搜索算法优化量化因子和比例因子,结果表明具有更好的全局搜索能力和搜索精度;RAHUL L等[6]利用遗传算法和进化策略对模糊自适应逻辑控制器进行了优化,减少了系统误差;LIANG Haibo 等[7]提出了一种改进的遗传算法优化模糊自适应控制器,提高了控制器的快速性、稳定性和鲁棒性;ARKADIUSZ A等[8]优化了粒子群模糊自适应PID,提高了无故障运行时间;MOHAMED A R S等[9]利用粒子群优化算法对模糊逻辑控制器进行了参数优化,提高了控制器动态性能和系统可靠性。不过这些优化算法在模糊自适应PID初始参数的寻优能力与收敛速度方面还有进一步改进的空间,因此需要寻求一种更好的优化算法。

综上,本研究运用了一种较新的野狗优化算法(Dingo Optimization Algorithm,DOA),其寻优能力和收敛速度均较好,可用于改进模糊自适应PID控制方法,提高控制器的动态性能。根据阀控马达和模糊自适应PID控制原理,提出野狗优化算法模糊自适应PID的控制方法。首先在MATLAB中编写阀控马达转速传递函数的m函数,通过野狗优化算法得到最优初始参数。其次,分别在AMESim和Simulink中建立液压系统与控制系统仿真模型并形成联合仿真模型[10]。最后,根据除雪撒盐车实际工况进行空载和突变干扰仿真试验,验证联合仿真模型的准确性,比较所提出的方法与传统优化算法在撒盐马达转速控制上的优势,并验证其用于除雪撒盐车阀控马达转速调控的可行性。

1 比例阀控液压马达原理

除雪撒盐车阀控马达电液伺服系统由电液比例阀、液压马达、液压泵、电机、单向节流阀及其他液压元件组成。其系统原理图如图1所示。

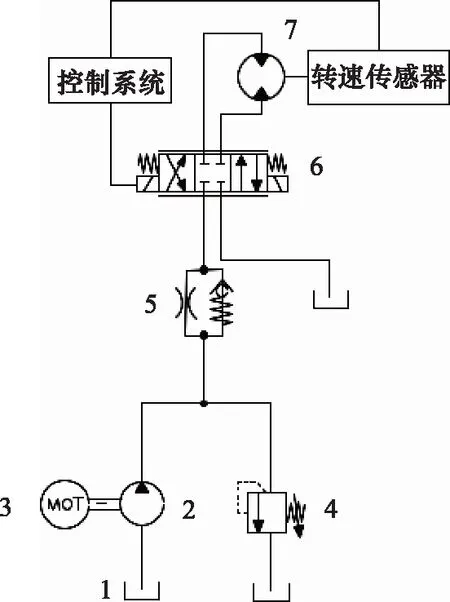
1.油箱 2.液压泵 3.电机 4.溢流阀 5.单向节流阀 6.电液伺服阀 7.液压马达图1 阀控马达电液伺服系统原理图Fig.1 Schematic diagram of valve-controlled motor electro-hydraulic servo system

阀控马达电液伺服系统原理:液压油经过液压泵2、单向节流阀5和电液伺服阀6传递到液压马达7并转换为马达转速,给定马达目标转速信号,转速传感器采集液压马达7的转速,将当前转速信号传递给控制系统,控制系统对当前转速信号进行调整并改变电液伺服阀6的电流大小,进而改变伺服阀开度与流量,最终实现马达7转速稳定在目标转速。

2 野狗优化算法简介

野狗优化算法模仿了澳大利亚野狗的社交行为:迫害行为、分组策略和清扫行为。根据三种社交行为制定了与四种规则相关的三种搜索策略[11]。算法流程图如图2所示。

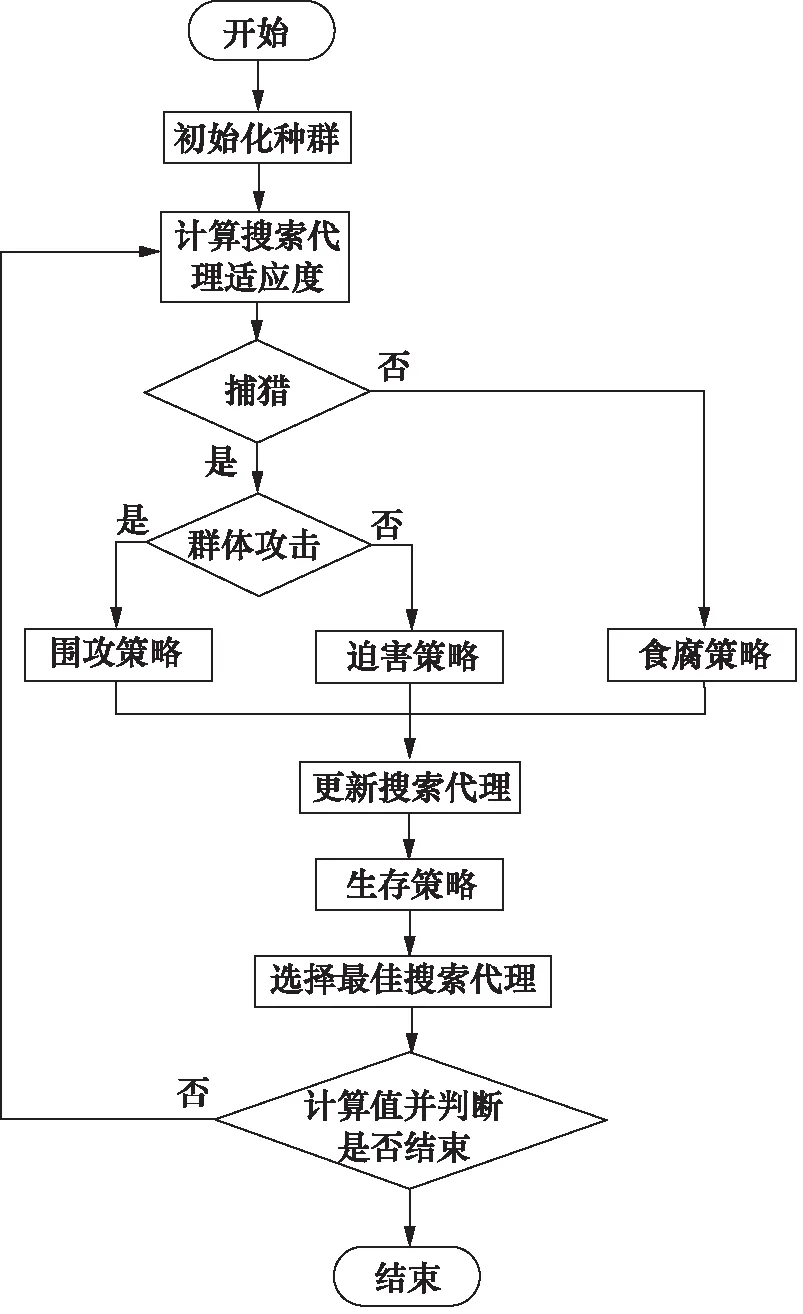
图2 野狗优化算法流程图Fig.2 Flow chart of dingo optimization algorithm

2.1 优化过程

1) 种群初始化

种群初始化公式如式(1)所示:

(1)

式中,lbi,ubi—— 个体下限和上限

randi—— [0,1]内的随机数

2) 搜索策略

(1) 围攻策略:当野狗进行狩猎捕捉大型猎物时,往往采取会成群包围的策略,这种行为如式(2)所示:

(2)

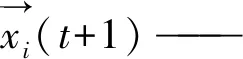
na—— 在[2,SizePop/2]的倒数中生成的随机整数,其中SizePop是野狗种群的总大小

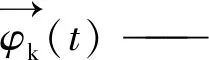
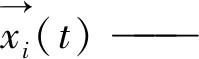
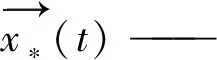
β1—— 是在[-2,2]范围内改变野狗轨迹大小的比例因子

(2) 迫害策略:野狗在捕捉小型猎物时往往是单独行动,此行为一直到捕获为止,如式(3)所示:

(3)

式中,β2—— [-1,1]之间均匀生成的随机数

r1—— 从1到最大搜索代理大小的区间内生成的随机数

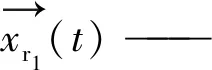
(3) 食腐策略:当野狗不狩猎时,为了维持生存,需要在栖息地附近搜寻腐肉,如式(4)所示:

(4)

式中,σ—— 随机生成的二进制数,σ∈{0,1}

(4) 野狗存活率:此策略用于描述野狗在自然环境生存下的生存概率,当存活率较低时,更新搜索代理。存活率如式(5)表示。

(5)

式中,fitnessmax,fitnessmin—— 当前一代中最差和最佳的适应度值

fitness(i) —— 第i个搜索代理的当前适应度值,此式的存活向量包含[0,1]区间内的归一化适应度

当存活率低于0.3时,被更新的搜索代理如式(6)所示:

(6)

式中,r1,r2—— 从1到最大搜索代理次数范围内的随机数,r1≠r2

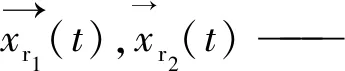
2.2 DOA对PID参数的优化步骤

在MATLAB中编写除雪撒盐车液压马达转速传递函数PID控制模型的m函数,选定一种最优指标作为目标函数,利用DOA优化算法求得目标函数最小值时的PID参数并完成优化。

本研究所用的除雪撒盐车阀控马达转速传递函数为[12]:

(7)

最优指标如式(8)所示:

(8)

式中,ω1,ω2,ω3—— 权值,取ω1=0.999,

ω2=0.001,ω3=2

u(t) —— 控制器输出值

e(t) —— 误差

tu—— 上升时间

u(t)=k(1)*x(1)+k(2)*x(2)+k(3)*x(3)

(9)

x(1)=e(t)

(10)

x(2)=(e(t)-e(1))/ts

(11)

x(3)=x(3)+e(t)*ts

(12)

式中,x(1),x(2),x(3) —— 比例、微分和积分的迭代参数

ts—— 采样时间,取0.001 s

误差计算公式如下:

e(t)=r-y(t)

(13)

y(t)=-den(2)*y_1-den(3)*y_2+

num(2)*u_1+num(3)*u_2

(14)

式中,e(t) —— 误差

r—— 目标值,取1000

y(t) —— 将传递函数离散化后的近似线性模型当前值

den(i),num(i) —— 离散化为差分方程后的分子和分母系数

目标函数如式(15)所示:

f=min(J(t))

(15)

在MATLAB中编写DOA优化算法m函数,参数设置为:搜索代理数量为100;迭代次数为500;PID参数上限为[50,50,50],下限为[15,25,5];捕猎或食腐概率为0.5;围攻策略或迫害策略概率为0.7。其他优化算法的PID参数上下限与DOA相同,各优化算法的除雪撒盐车阀控马达传递函数模糊自适应PID最佳初始值如表1所示。

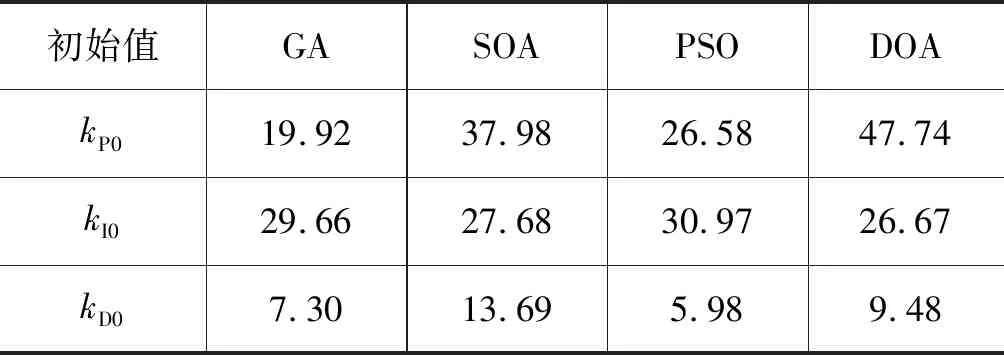
表1 各优化算法下的PID初始值Tab.1 Initial PID value under each optimization algorithm

3 模糊自适应PID控制原理

模糊自适应PID控制是在传统PID控制策略的基础上,将专家经验与模糊数学理论进行结合形成的智能控制方法。其控制原理图如图3所示。

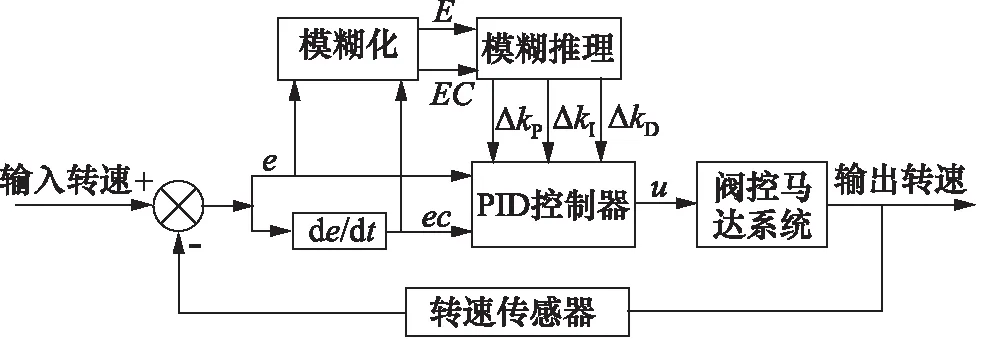
图3 模糊自适应PID控制原理图Fig.3 Schematic diagram of fuzzy adaptive PID control

转速传感器采样得到当前转速,与目标转速进行比较,得到转速偏差e和偏差变化率ec,将其作为输入变量输入到模糊控制器中,模糊化为E和EC两个模糊量,随后进行模糊推理及去模糊化得到比例系数变化量、积分系数变化量和微分系数变化量三个输出变量,实现kP,kI和kD在线调整,然后经过模糊自适应PID控制器调整得到输出量u即调整后的马达转速。重复上述过程,直到当前转速与目标转速相等,至此,实现液压马达恒转速控制。其中,kP,kI和kD由初始值和变化量确定,计算公式如下:

kP=kP0+ΔkP

(16)

kI=kI0+ΔkI

(17)

kD=kD0+ΔkD

(18)

式中, ΔkP,ΔkI,ΔkD—— 比例系数、积分系数、微分系数的变化量,由模糊控制器确定

4 提出的野狗优化算法模糊自适应PID控制方法

4.1 模糊自适应PID控制器的设计

1) 模糊控制器的选取

选取液压马达转速偏差e和偏差变化率ec作为模糊控制器的输入变量,选取比例系数变化量ΔkP、积分系数变化量ΔkI和微分系数变化量ΔkD作为模糊控制器的输出变量,因此本研究选择两输入三输出的模糊控制器。

2) 模糊子集的选取

模糊子集越多,模糊控制器对变量的描述就越准确,控制效果越好,结果越精确,但是过多的模糊子集会导致模糊规则变多,计算速度变慢;过少的模糊子集可能会使部分模糊规则没有相互适应, 结果收敛性不好[13-14]。因此,本研究选用七个模糊子集{NB,NM,NS,ZO,PS,PM,PB}={负大,负中,负小,零,正小,正中,正大}。

3) 量化因子与比例因子的选取

输入模糊控制器的量为传感器测得的实际值,而模糊推理需要用到模糊量,因此要将输入的实际值转换为模糊量。同样地,由模糊控制器输出的量为模糊量,需要将输出的模糊量转换为实际值。输入量的基本论域与模糊论域的转换由量化因子确定,输出量的模糊论域与基本论域的转化由比例因子确定[15-16]。量化因子与比例因子确定方法如下:

设:

e的基本论域为[-xe,xe],模糊论域为{-n,-(n-1),-(n-2),…,n-2,n-1,n};

ec的基本论域为[-xec,xec],模糊论域为{-m,-(m-1),-(m-2),…,m-2,m-1,m};

ΔkP的基本论域为[-xp,xp],模糊论域为{-p,-(p-1),-(p-2),…,p-2,p-1,p};

ΔkI的基本论域为[-xi,xi],模糊论域为{-I,-(i-1),-(i-2),…,i-2,i-1,i};

ΔkD的基本论域为[-xd,xd],模糊论域为{-d,-(d-1),-(d-2),…,d-2,d-1,d};

则:

(19)

(20)

(21)

(22)

(23)

式中,Ke—— 偏差e的量化因子

Kec—— 偏差变化率ec的量化因子

KΔkP—— 比例系数变化量ΔkP的比例因子

KΔkI—— 积分系数变化量ΔkI的比例因子

KΔkD—— 微分系数变化量ΔkD的比例因子

所取基本论域、模糊论域及计算得到得量化因子与比例因子如表2所示。

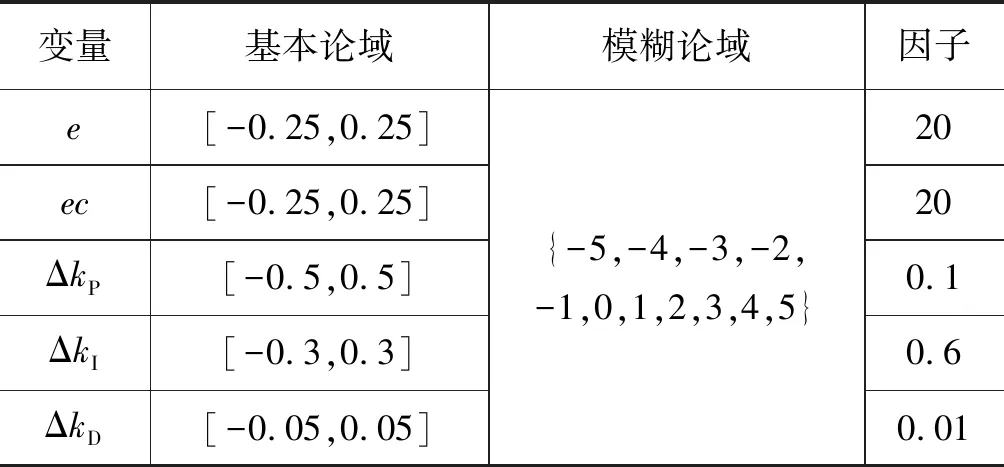
表2 论域与因子取值Tab.2 Domain and factor values

4) 隶属度函数的选取

一般采用三角形和基于多项式曲线的隶属度函数, 其中基于多项式曲线的隶属度函数包括Z形和S形隶属度函数[17]。本研究NB采用Z形隶属度函数,PB采用S形隶属度函数,NM、NS、ZO、PS、PM采用三角形隶属度函数,e和ec隶属度函数如图4所示,ΔkP、ΔkI和ΔkD隶属度函数如图5所示。

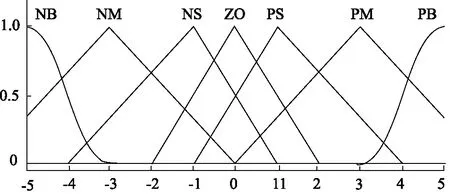
图4 e和ec的隶属度函数Fig.4 Membership functions of e and ec

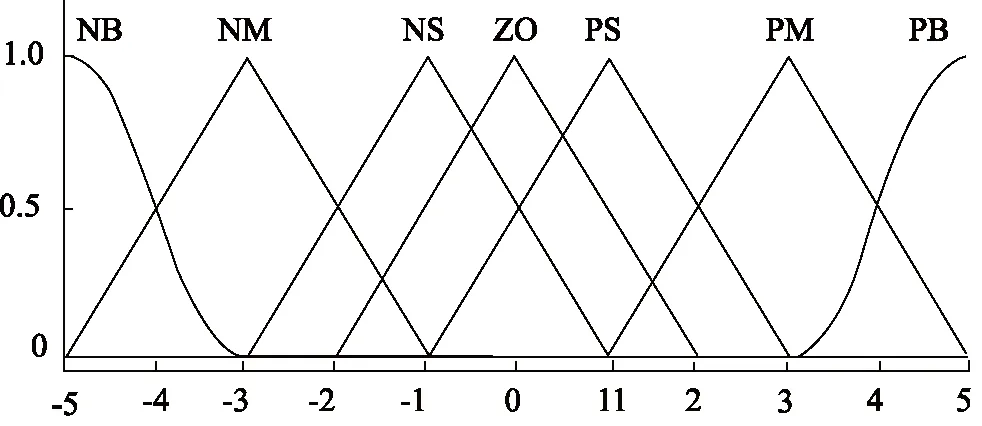
图5 ΔkP、ΔkI,ΔkD的隶属度函数Fig.5 Membership functions of ΔkP,ΔkI and ΔkD

5) 模糊控制规则的制定

模糊控制规则是模糊控制算法的集合,有效的模糊控制规则可以增强模糊自适应PID控制效果,减小系统误差[18-19]。模糊控制规则需根据模糊控制器输入变量与输出变量的关系得到:

(1)kp决定系统响应速度。在调节初期,偏差e和偏差变化率ec较大,因此选取较大的kp值以提高响应速度,减小稳态误差;在调节中期,选取较小的kp值以降低系统超调量;在调节后期,偏差e和偏差变化率ec很小,增大kp以减小静态误差。

(2)kI的主要作用为消除稳态误差。在调节初期,应取较小的kI值以减小系统超调量;在调节中期,为避免影响系统稳定性,应取较为适中的kI值;在调节后期,应取较大的kI值以减小静态误差。

(3)kD用于改变系统动态特性。在调节初期,为防止偏差e过大,应引入一个较大的修正信号以降低超调量,因此取较大的kD值;在调节中期,由于PID调节特性对kD值的变化很敏感,应保持kD值不变或适当减小;在调节后期,为缩短调节时间、减小制动作用,应减小kD值。

根据上述模糊控制规则关系,制定如表3所示的模糊控制规则表。

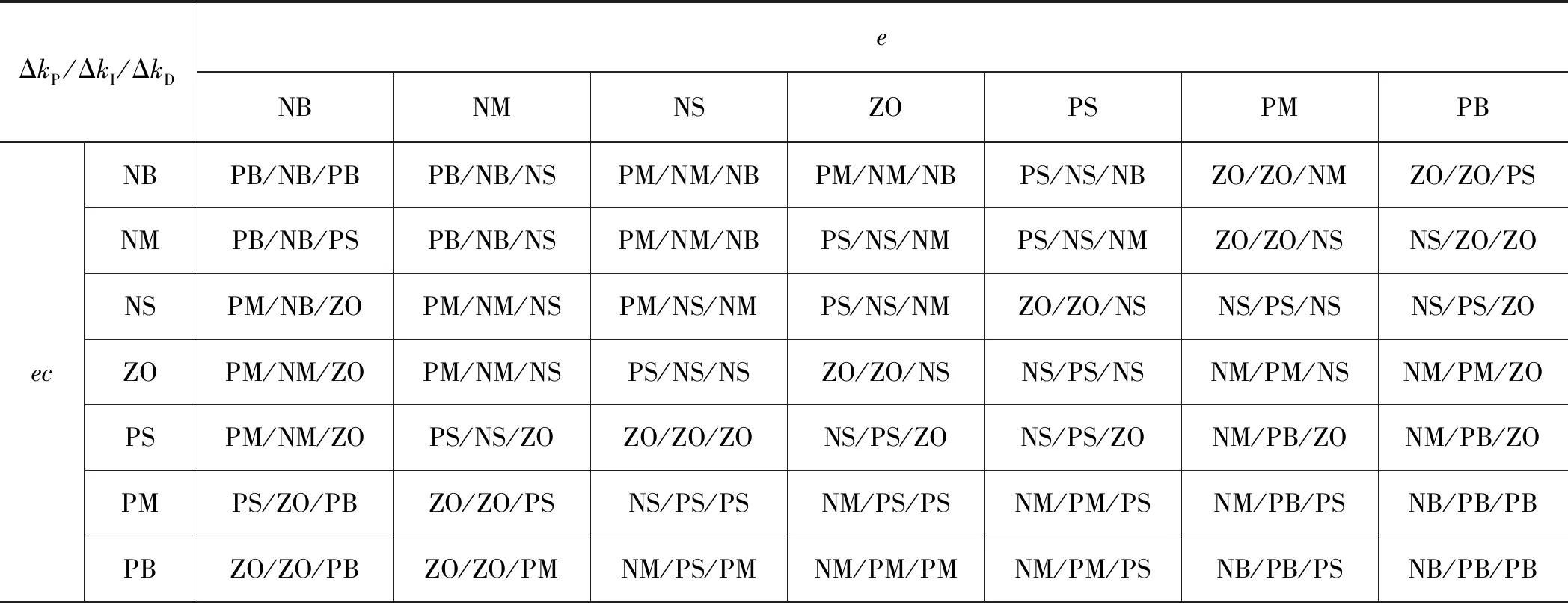
表3 模糊控制规则表Tab.3 Fuzzy control rules table

根据制定的模糊规则表,形成49条模糊规则:

Rule1:If(eis NB) and (ecis NB) then (ΔkPis PB)(ΔkIis NB)(ΔkDis PS)

Rule2:If(eis NB) and (ecis NM) then (ΔkPis PB)(ΔkIis NB)(ΔkDis PS)

Rule3:If(eis NB) and (ecis NS) then (ΔkPis PM)(ΔkIis NB)(ΔkDis ZO)

…………

Rule49:If(eis PB) and (ecis PB) then (ΔkPis NB)(ΔkIis PB)(ΔkDis PB

模糊输出曲面观测可以直观的看出模糊规则是否合理,曲面越平滑,控制效果越好[20]。ΔkP、ΔkI、ΔkD的模糊输出曲面如图6～图8所示,模糊输出曲面比较平滑,因此本次制定的模糊控制规则合理。

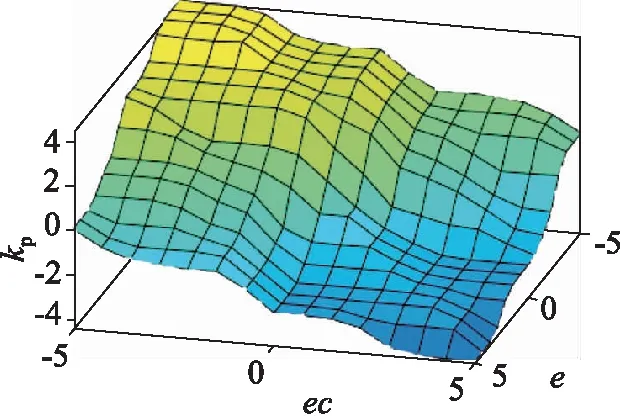
图6 ΔkP的模糊输出曲面Fig.6 Fuzzy output surface of ΔkP

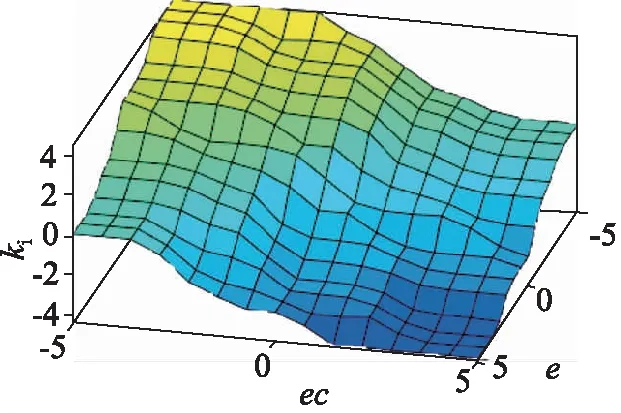
图7 ΔkI的模糊输出曲面Fig.7 Fuzzy output surface of ΔkI

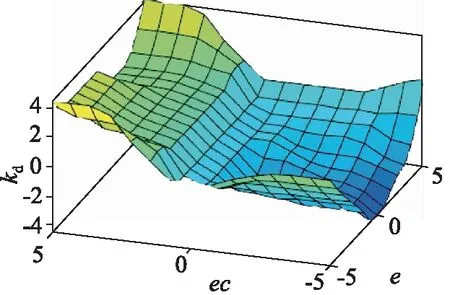
图8 ΔkD的模糊输出曲面Fig.8 Fuzzy output surface of ΔkD

4.2 联合仿真模型的建立

1) AMESim中液压系统的建立

根据比例阀控液压马达原理,在AMESim中建立如图9所示的液压系统仿真模型,其中,GA、PSO、SOA和DOA的液压系统模型与液压元件参数完全相同,液压元件主要参数如表4所示。

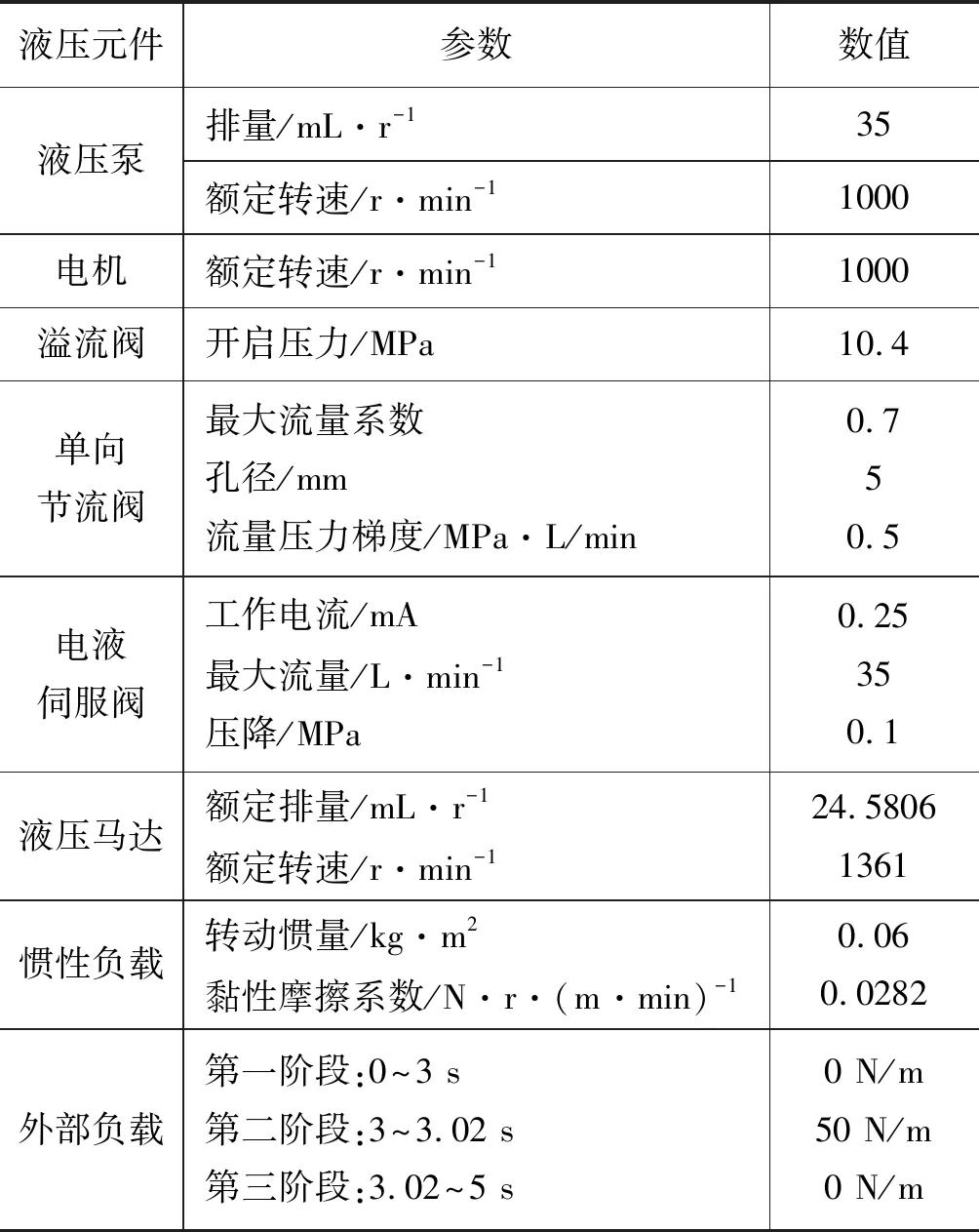
表4 液压元件主要参数Tab.4 Main parameters of hydraulic components

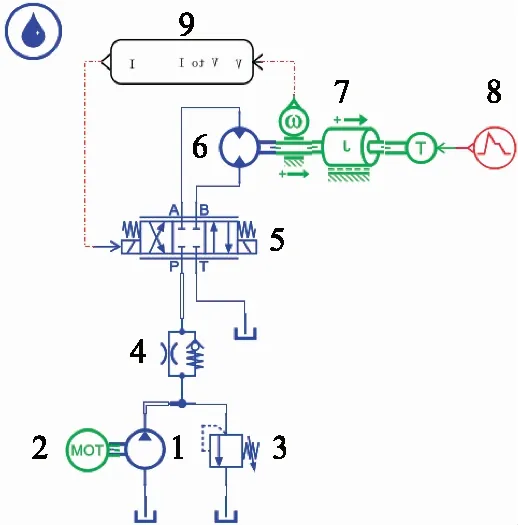
1.液压泵 2.电机 3.溢流阀 4.单向节流阀 5.电液伺服阀 6.液压马达 7.惯性负载 8.外部负载 9.联合仿真接口图9 阀控马达液压系统仿真模型Fig.9 Simulation model of valve-controlled motor hydraulic system

2) Simulink中控制系统的建立

根据模糊自适应PID控制原理,在Simulink中搭建如图10所示控制系统模型,其中,GA、PSO、SOA和DOA的模糊控制器、模糊子集、量化因子、比例因子、隶属度函数及模糊控制规则完全相同,仅模糊自适应PID的初始参数不同。

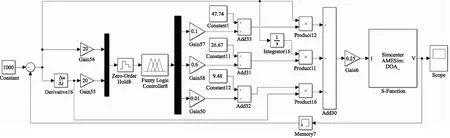
图10 阀控马达控制系统仿真模型Fig.10 Simulation model of valve-controlled motor control system

5 仿真结果与分析

根据除雪撒盐车撒盐马达实际工况,将仿真分为两个试验阶段:

(1) 空载状态试验:在初始状态不施加外部负载,模拟撒盐马达正常使用工况。得到马达转速达到峰值的时间、超调量及稳定时间,比较四种优化算法下的响应速度、超调控制能力及平稳性;

(2) 突变干扰试验:在仿真第3 s时对马达施加50 N/m的突变干扰,持续0.02 s,模拟撒盐马达受液压冲击等突变干扰时的工况。得到马达转速波动与恢复时间,比较四种优化算法的抗干扰能力。

联合仿真模型建立完成后,在Simulink中运行联合仿真,并在AMESim中观察联合仿真结果,马达转速随时间变化仿真结果如图11所示,四种优化算法下的马达转速变化如表5所示。

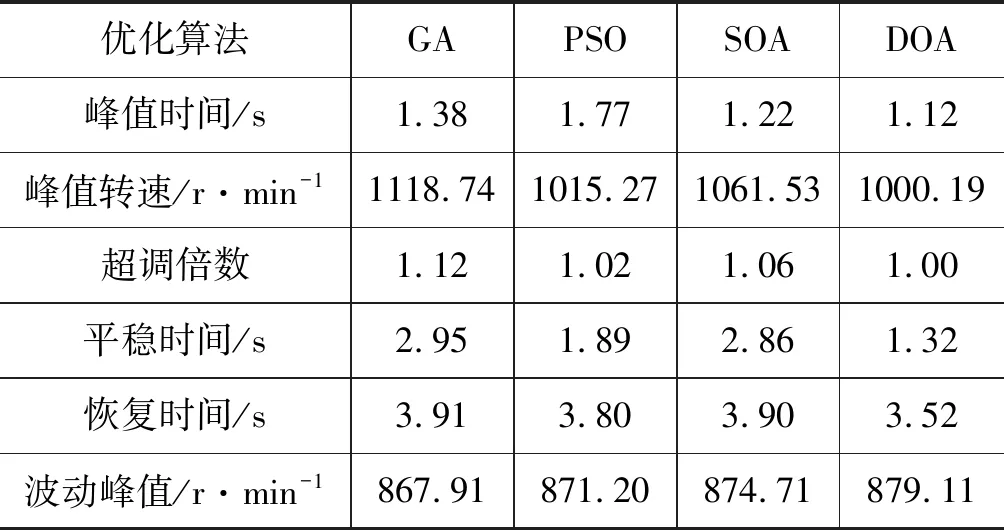
表5 各优化算法下的马达转速变化Tab.5 Variation of motor speed under each optimization algorithm

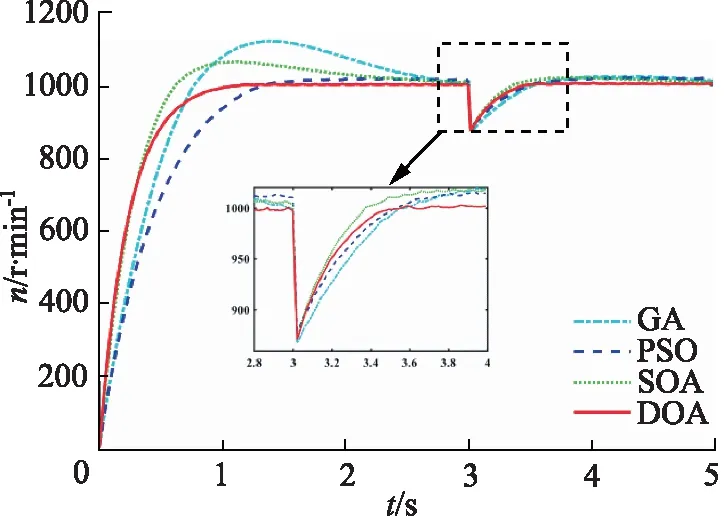
图11 马达转速变化Fig.11 Motor speed variation

通过仿真结果可以看出,DOA在转速上升阶段的响应速度最快,仿真第1.12 s时就已经达到转速峰值,第1.32 s时达到平稳运行状态,并且几乎没有出现超调和转速波动;在受到突变干扰时,DOA的转速波动最小,为-120.89 r/min,在转速恢复阶段没有出现转速超调现象,转速在第3.52 s即用时0.52 s恢复为平稳运行状态,所用时间最短。

综上,DOA优化算法在模糊自适应PID的超调量控制、响应速度、抗突变干扰能力和鲁棒性均优于GA、PSO和SOA,DOA具有较强的稳态性能和动态响应能力。所提出的DOA模糊自适应PID控制方法下的除雪撒盐车阀控马达电液伺服系统的转速调控能力明显提高,对改善除雪撒盐车阀控马达电液伺服系统既提高除雪撒盐车工作性能具有实际应用意义。

6 结论

本研究针对除雪撒盐车阀控马达电液伺服系统,提出了一种基于野狗优化算法的模糊自适应PID控制方法,优化了模糊自适应PID初始参数,实现了撒盐马达恒转速调控,并得出以下结论:

(1) 建立的AMESim与Simulink联合仿真能够较为准确地模拟实际工况下的除雪撒盐车阀控马达电液伺服系统转速变化情况,可用于阀控马达系统相关仿真研究;

(2) DOA模糊自适应PID控制方法相比于GA、PSO和SOA传统优化算法超调量小、响应速度快、抗突变干扰能力强;

(3) DOA模糊自适应PID控制方法可用于除雪撒盐车阀控马达电液伺服系统,能够提高阀控马达的控制效果,满足除雪撒盐车正常工作;

(4) DOA模糊自适应PID控制方法可延伸到其他机械的阀控马达或阀控缸液压系统,同时可用于转速、位移的同步控制研究。