基于机舱负载特性的力控伺服加载系统仿真分析

赵 峰, 李化顺, 邱 华,, 刘 旭, 俞 滨

(1.新乡航空工业(集团)有限公司, 河南 新乡 453000;2.燕山大学 机械工程学院, 河北 秦皇岛 066004)

引言

20世纪60年代以来航空运输逐步兴起[1],具有集装化运输能力的民用运输机种类逐渐繁多,如客机A380与波音747、客货混装机747-200COMBI和全货机747-200F等[2],具备高效率、高机动性等优势,得到了远程运输领域相关研究人员的重视。

民用运输机的机舱承载着乘客、各类货物与各型航空集装单元,以A-380与747-8f为例,载重量在150 t 左右。机舱负载特性影响着运输机承载能力与重心平衡,进而影响飞行安全[3-5]。因此需要在运输机正式投入使用之前,使用加载系统对机舱进行加载实验,分析其响应特性以及加载频率范围等负载特性,可为确定运输机负载性能、故障排除和后续构型改进提供指导建议[6]。

当前加载系统一般分为机械式、电动和伺服等三种,其中伺服加载系统以输出功率大、加载力范围广、动力传输便捷等优势得到了广泛研究与应用[7]。魏亮亮等[8]建立了起落架收放机构动力学模型,仿真分析了模拟伺服加载下的负载性;SHI J 等[9]、PISANO A A等[10]和张柁等[11]研究了飞机强度试验结构伺服加载系统与力控加载方法,实现了单点大载荷的精准施加[12];黄勋伟研究了面向航空电动静液作动器的伺服加载系统,并结合航空载荷谱进行了仿真分析[13];TRON X L[14]针对在空客A380使用的电动静液作动器进行了加载分析与负载性能验证;王靖等[15]对静力强度伺服加载系统进行了设计,可完成多工况加载;燕晨耀等[16]将力控加载技术引入到结构静力伺服加载平台;李崇等[17]研究了大型飞机机舱内的复杂应力场,开发出了一种多载荷联合加载平台。

本研究针对机舱载荷模拟加载控制,设计液压加载系统的机械结构与加载方式,建立了力伺服控制数学模型提高控制精度,对单个伺服缸与多套并联加载系统进行了负载特性仿真分析。

1 加载系统结构设计

运输机机舱承受的载荷至少要达到上百吨,对于加载系统的力输出有着硬性的需求。因此选择以液压系统设计加载系统,通过多个伺服缸并联的方式模拟不同位置的载荷。

1.1 机械结构设计

方案采用固定机架安装并联多套伺服缸伸出的方式进行模拟加载,以平台模拟机舱作为载荷施加位置,机械结构采用小块钢板拼接的形式以防止应力变形,采用三角架的支撑结构可以增加支撑强度,其具体结构如图1所示。

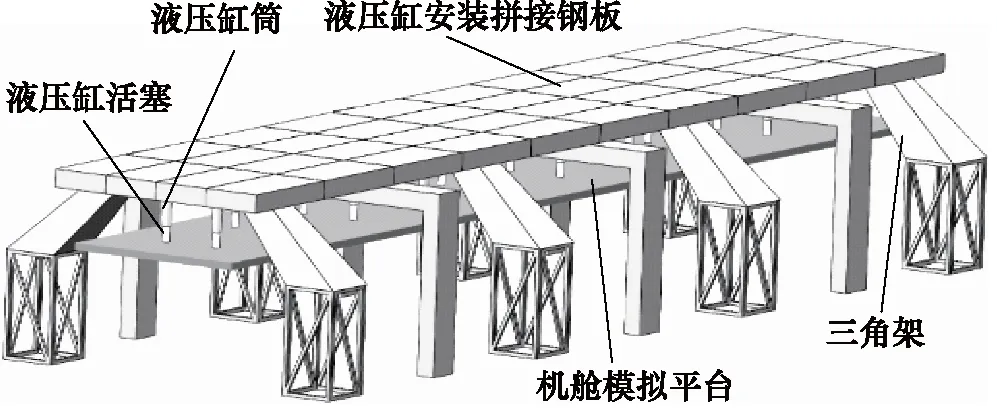
图1 加载系统机械结构Fig.1 Test platform for gas-liquid linkage system

1.2 加载方式设计

加载系统包含左右各10个均匀分布在试验台两侧的伺服缸,通过不同的伺服缸组合作为不同的加载方式对机舱进行均匀载荷施加(图中蓝色部分代表施加载荷的伺服缸),模拟机舱内乘客、各类货物与各型航空集装单元的摆放方式,如图2所示。

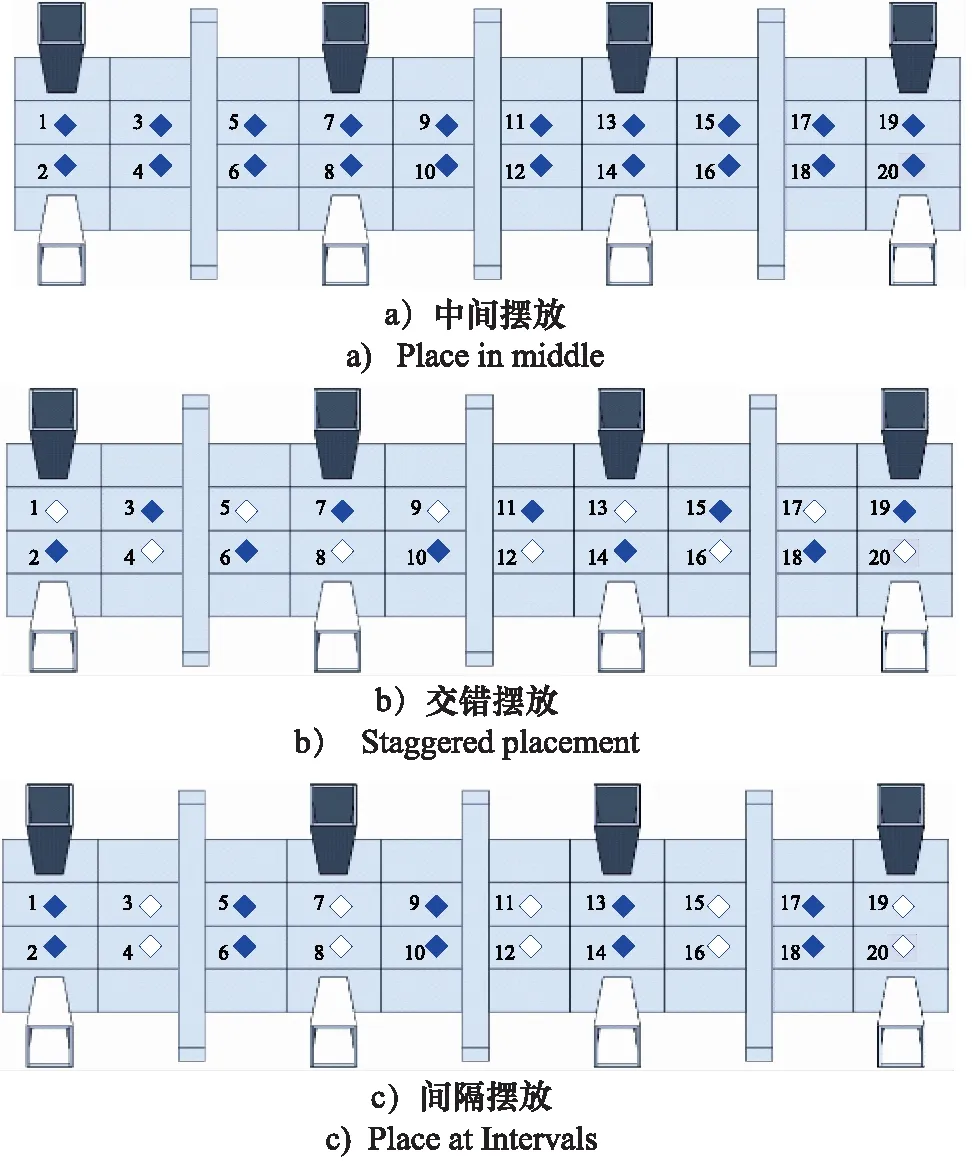
图2 加载方式示意图Fig.2 Loading mode diagram

2 加载系统力控伺服数学模型建立

将加载系统内的伺服阀近似看做二阶振荡环节,由此可以推导出伺服阀阀芯位移与放大板控制输入电压间的传递函数如下:

(1)

式中,Kaxv—— 伺服阀增益

ζ—— 伺服阀阻尼比

ω—— 伺服阀固有频率

相比阀口节流压力损失,管路与阀腔中的压力损失要小得多,因此在计算中将其省略;其中,压力与流量的非线性关系通过伺服阀的进油流量进行表达,公式如式(2)所示:

q1=KdXv×

(2)

伺服阀回油流量可表示为:

q2=KdXv×

(3)

式中,Xv—— 伺服阀阀芯位移

ps—— 系统供油压力

p1—— 伺服缸左腔压力

p2—— 伺服缸右腔压力

p0—— 系统回油压力

Kd—— 折算流量系数

其中,折算流量系数Kd的表达式为:

(4)

式中,Cd—— 滑阀节流口流量系数

W—— 面积梯度

ρ—— 液压油密度

对于伺服阀控制对称缸液压系统,其受到伺服缸泄漏及油液压缩性等因素的影响,因此缸进油流量及进油腔容积通过式(5)来表达:

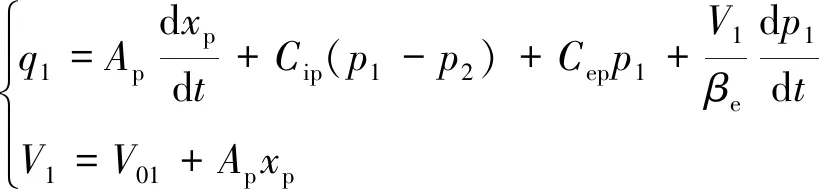
(5)

同理,缸回油流量和回油腔容积通过式(6)来表达:

(6)

式中,Ap—— 伺服缸活塞有效面积

xp—— 伺服缸活塞位移

Cip—— 伺服缸内泄漏系数

Cep—— 伺服缸外泄漏系数

βe—— 有效体积模量

V01—— 进油腔初始容积

V02—— 回油腔初始容积

其中,V01和V02和伺服缸流量q可表示为:

(7)

式中,Vg1—— 伺服阀与伺服缸进油连接流道容积

Vg2—— 伺服阀与伺服缸回油连接流道容积

L—— 伺服缸活塞总行程

L0—— 伺服缸活塞初始位置

受到负载特性对力控加载系统的影响,伺服缸输出力与负载力的平衡方程为:

Ff+FL

(8)

式中,F—— 伺服缸的输出力

mt—— 折算到伺服缸活塞上总质量

K—— 负载刚度

Bp—— 黏性阻尼系数

Ff—— 库仑摩擦力

FL—— 作用在阀控缸力控制系统活塞的任意外负载力

xL—— 外负载位置

力传感器反馈电压与伺服缸活塞输出力的传递函数为:

(9)

式中,KF—— 力传感器增益

力偏差为:

Ef=Fr-Fs

Fs=ΔFs+F0

(10)

式中,F0—— 外负载位置干扰引起的系统力偏差

联立式(1)～式(10),建立加载系统力控伺服数学模型如图3所示。

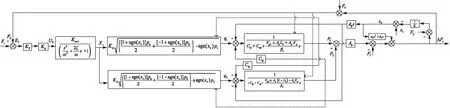
图3 加载系统力控伺服数学模型Fig.3 Force control servo mathematical model of loading system

3 加载系统负载特性仿真分析

加载系统的液压系统为20阀并联系统,每个伺服阀独立控制一个加载缸,因此系统中的20个加载缸是相互独立而不互相影响的。

以A-380与747-8f为例,载重量在150 t左右,按四倍能力设计即出力为600 t,则平均每个伺服缸需出力约300 kN。系统仿真模型其余参数及初值如表1所示。

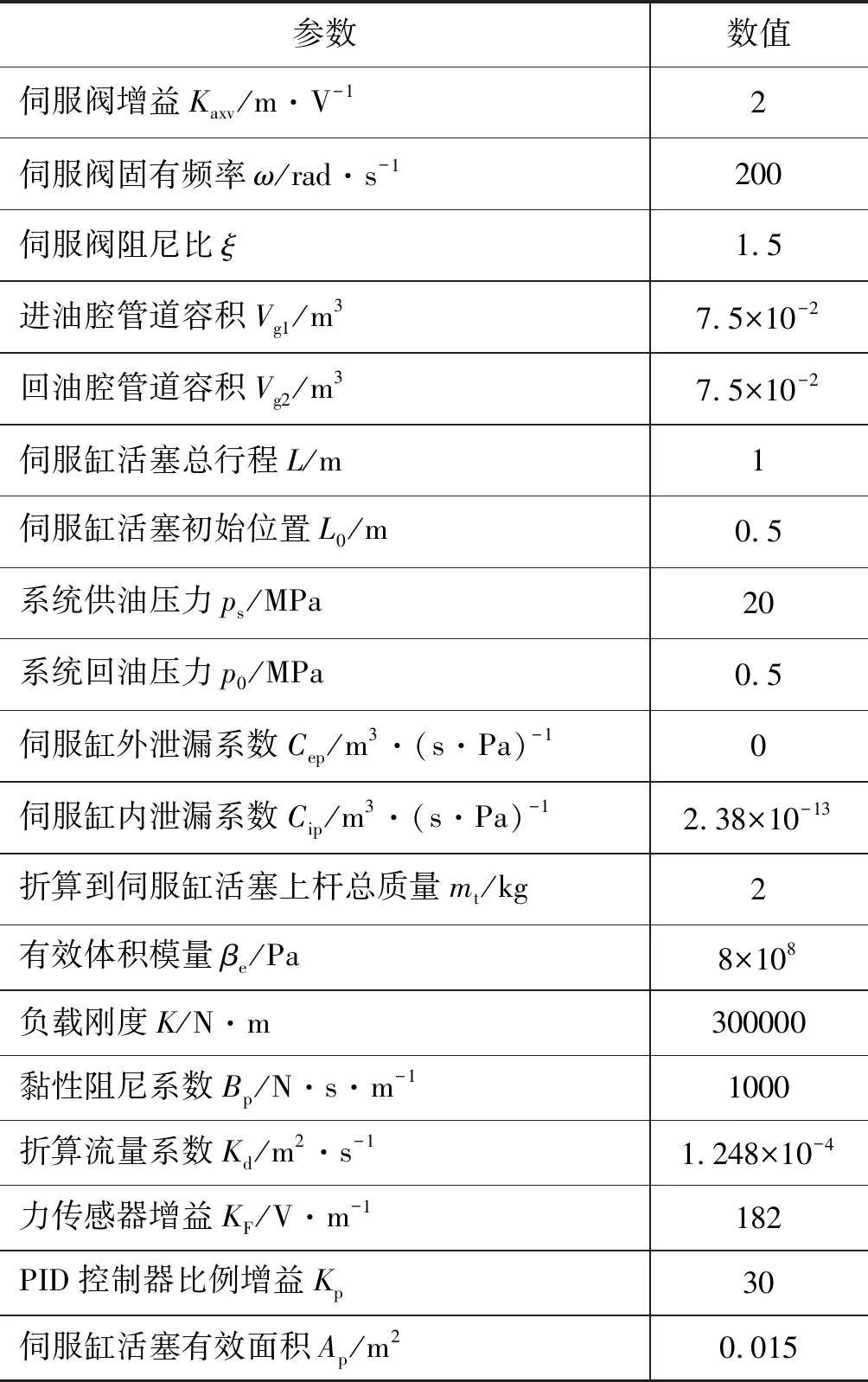
表1 加载伺服系统部分参数表Tab.1 Partial Parameters of Loading Servo System

3.1 单缸仿真建模

使用表1提供的数据,通过SolidWorks建立单缸三维模型,并正确的设置好各个零部件之间的配合方式;将其导入到MATLAB中,得到单缸仿真模型如图4所示,建立力控伺服加载控制模型如图5所示。

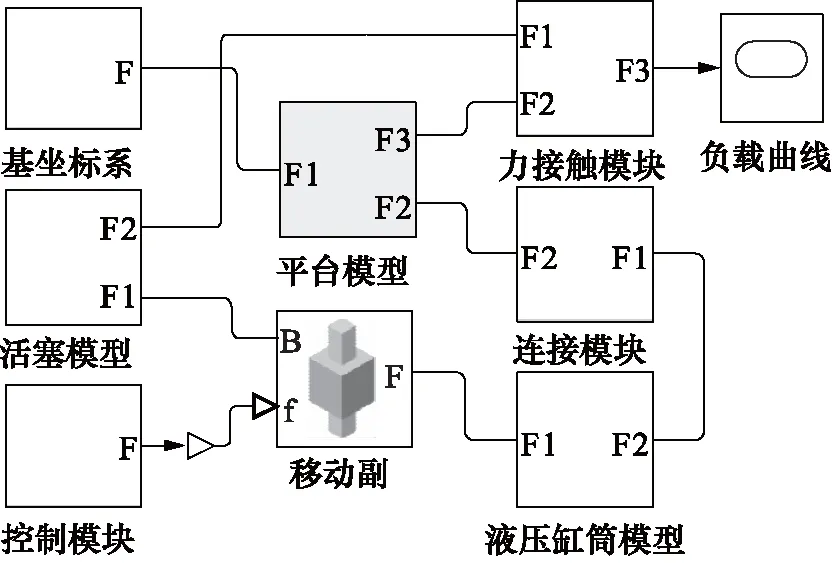
图4 单缸仿真模型Fig.4 Single cylinder simulation model

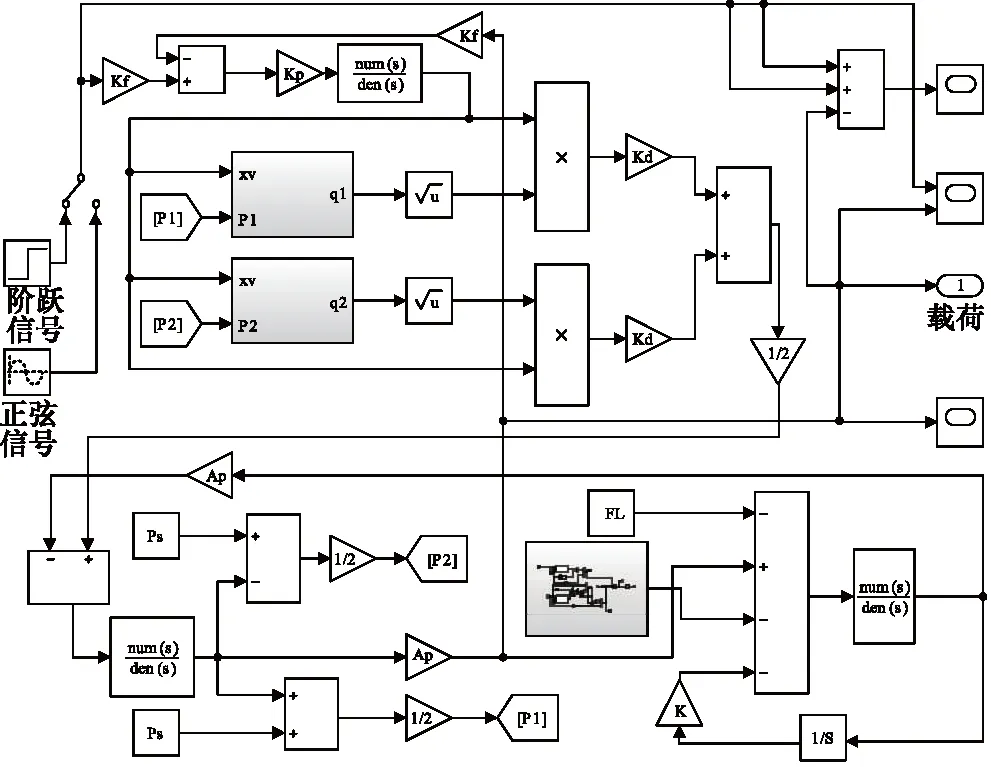
图5 单缸力控伺服加载控制模型Fig.5 Single cylinder force control servo loading control model

3.2 单缸负载特性仿真分析

1) 阶跃力响应分析

为了直观表征加载系统的单缸活塞动作的超调量、快速性和稳态精度,首先以力位移阶跃响应曲线评价系统的动态特性。在300 kN载荷加载的仿真过程中,总仿真时长为4 s,前1 s的动作是伺服缸杆下降到接触平台,此过程不做重点研究,着重考虑1～4 s的载荷施加的仿真过程。以2号缸为例,其受力大小及位移与图6所示一致。

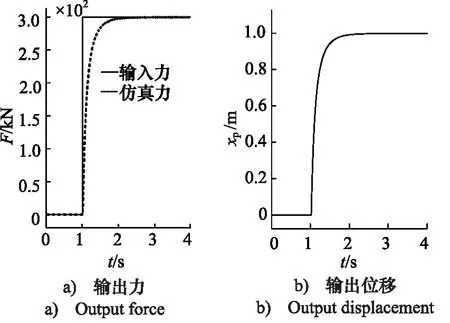
图6 阶跃信号下单缸仿真曲线Fig.6 Single cylinder simulation curve of step signal

在仿真进行到1 s之后,由于伺服阀打开,伺服缸在压力作用下逐渐伸出。在0～1 s期间,伺服缸活塞缓慢伸出,此时出力很小,速度较快;1～4 s期间伺服缸活塞一直接触机舱并持续输出300 kN的力。

2) 正弦力响应分析

为了确定系统加载频率范围,分别给定5 Hz,13 Hz,15 Hz的300 kN正弦信号载荷,单缸仿真曲线如图7所示。

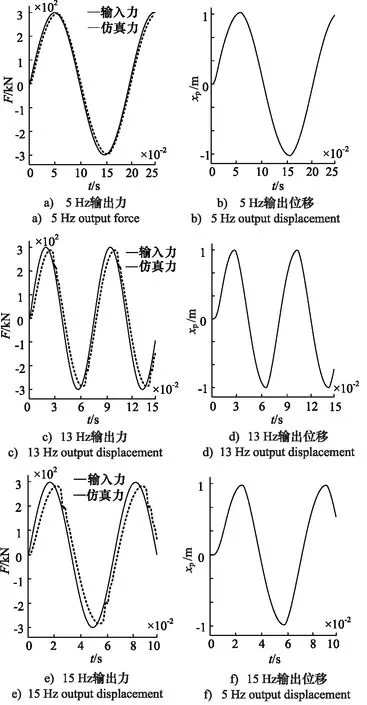
图7 正弦信号下单缸仿真曲线Fig.7 Single cylinder simulation curve under sinusoidal signal

正弦信号下,当给定频率为5 Hz时整体输出力的波动范围为6.8%,13 Hz时整体输出力的波动范围为14.8%,15 Hz时整体输出力的波动范围是18.3%。13 Hz时可以保证跟随全过程中的最大误差均控制在15%以内,能够实现满足加载要求的力控精度;15 Hz时跟随全过程中的最大误差较大,并不建议采用。实际上,加载伺服系统加载频率达到13 Hz,已经基本满足民用运输机装载质量变化和装载位置变化的模拟加载需求,后续将采用控制优化的方法进一步提高动态加载性能。

3) PID优化响应分析

采用工程中最常用的PID调节和结构不变原理提高频率至16 Hz,结构不变性原理是通过对系统位移干扰信号进行前馈补偿来保证力控精度,同时并不影响系统的稳定且结构简单、效果较好,所以被广泛应用在控制领域。提升了动态响应性能,其跟随曲线如图8所示。

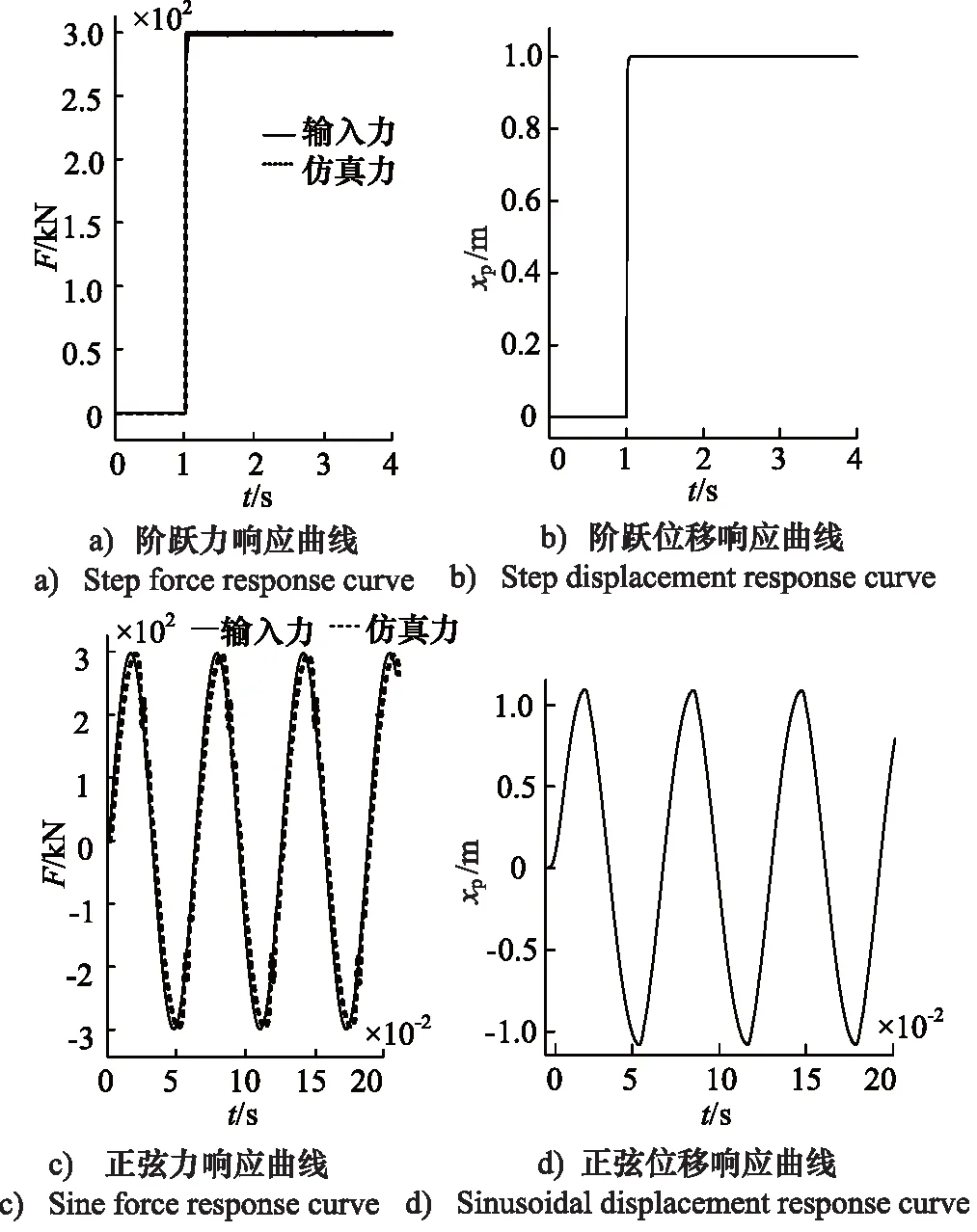
图8 PID优化后的单缸负载曲线Fig.8 Single cylinder load curve after PID optimization

3.3 加载系统仿真建模

和单套系统同理,使用表1提供的数据,建立二十套伺服缸组合形成的加载系统仿真模型如图9所示,加载方式如图2所示。

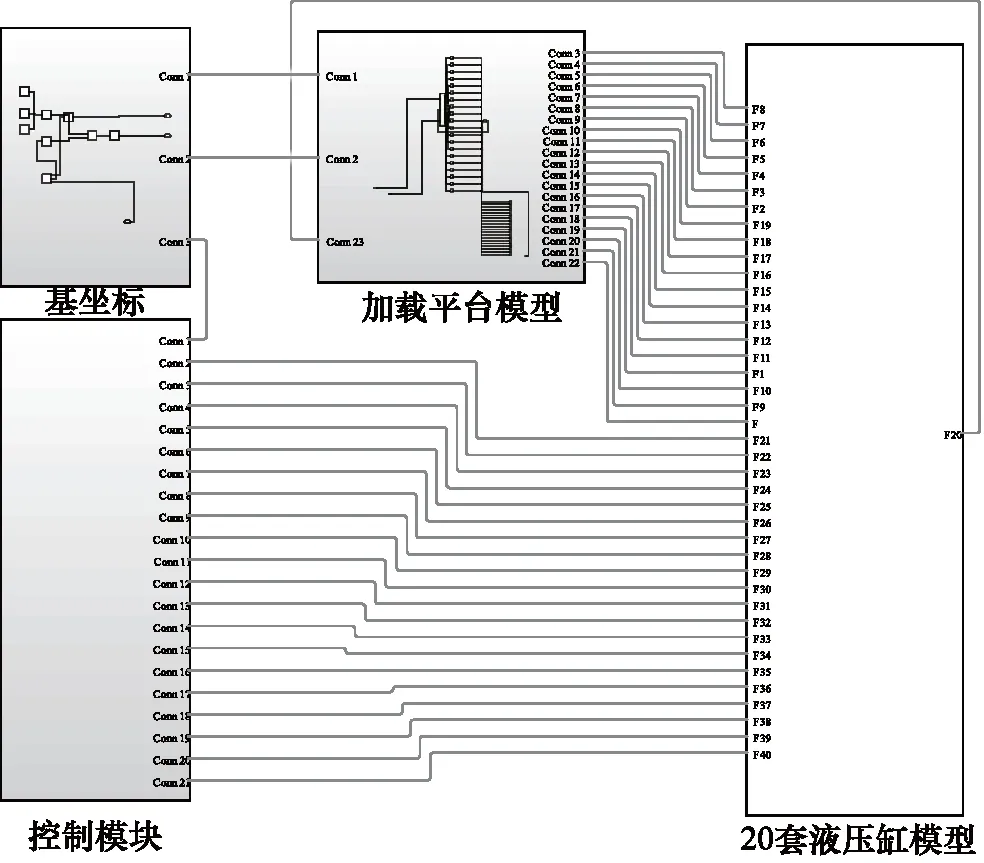
图9 加载系统仿真模型Fig.9 Loading system simulation model

在加载系统工作过程中,控制模块用于控制20套阀控缸模型,以单缸出力为输入,产生相应的流量,从而使伺服缸伸出,完成力加载。

3.4 加载系统负载特性仿真分析

1) 位置干扰下的负载特性

考虑到实际加载的过程中,承载物体会产生微小的变形。针对这种情况进行模拟,以2号缸为例,给定300 kN的恒驱动力,形成有位置误差的工况,缸出力如图10所示。

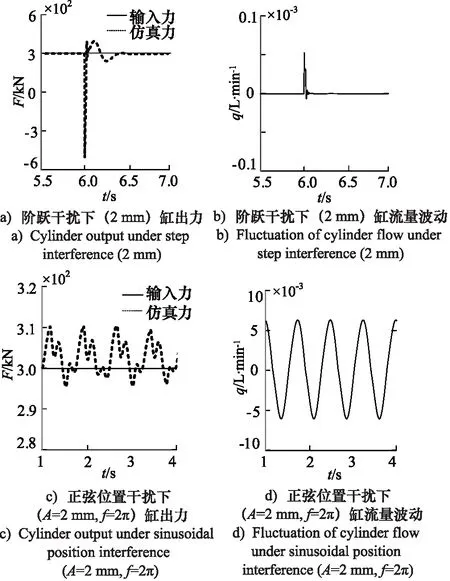
图10 位置干扰下加载系统仿真曲线Fig.10 Simulation curve of loading system with position interference

从图10中可以看出,伺服缸在阶跃干扰下的输出力基本稳定在300 kN,而对正弦干扰下的输出力则在300 kN附近有着一定的波动;系统流量随着出力的波动进行波动。

2) 偏载工况下的仿真结果

机舱工作过程中,除均匀载荷施加的工况,偏载工况也较容易出现。因此在仿真模拟中,选择1,2,3号缸,分别给定100,200,300 kN的驱动力,其余缸给定300 kN驱动力,实现偏载工况。对应的各缸出力如图11所示。

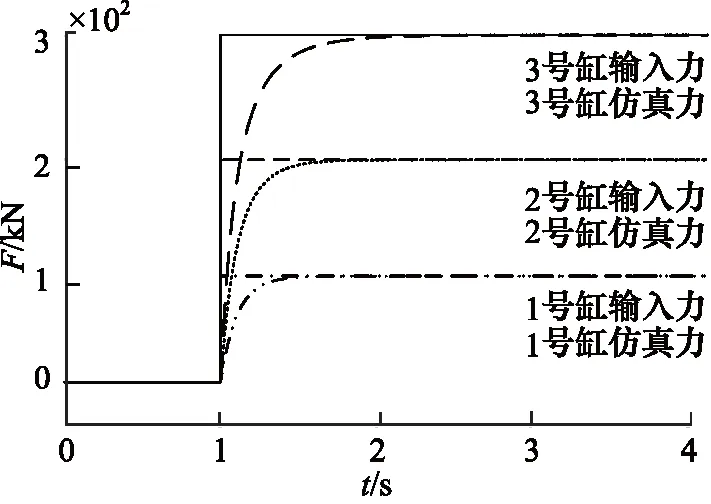
图11 偏载工况下加载系统仿真曲线Fig.11 Simulation curve of loading system under off-load condition

从图11中可以对应看出,伺服缸可以快速而稳定的输出力。

4 结论

本研究针对机舱载荷模拟加载控制,设计了一种力控伺服加载系统的机械结构与加载方式,并基于系统控制模型,分别对单伺服缸与由多伺服缸组成的加载系统进行了不同响应信号与工况下的负载特性仿真分析,验证了该系统的有效性为民用运输机的地面加载状态模拟提供了一种加载设计方案和建模控制方法。研究结果如下:

(1) 阶跃信号下,单缸与加载系统的力响应速度好,在1.06 s达到了300 kN,同时位移也达到了1 m;

(2) 正弦信号下,当给定频率为5 Hz时整体输出力的波动范围为6.8%,13 Hz时整体输出力的波动范围为14.8%,15 Hz时整体输出力的波动范围是18.3%。13 Hz时可以保证跟随全过程中的最大误差均控制在15%以内,已经基本满足民用运输机装载质量变化和装载位置变化的模拟加载需求;采用工程中最常用的PID调节和结构不变原理提高加载频率至16 Hz,进一步提升了加载系统动态响应性能。

(3) 阶跃位置干扰下加载系统单缸的输出力基本稳定在300 kN,正弦位置干扰下加载系统单缸的输出力波动范围为3.3%,正弦位置干扰下的流量波动为0.013 L/min,同时偏载工况下加载系统仍然可以快速而稳定的输出的力。