管道周向二维振动线阵视觉条纹同步测量

钟剑锋,涂 钊,李思钰,刘东明,池守疆,黄跃鑫,钟舜聪

(福建省太赫兹功能器件与智能传感重点实验室,福州大学,福建福州 350108)

0 引言

管道广泛应用于各行各业的固体、液体、气体的输送。在众多应用领域中,由于管道使用年限的增加以及管道输送物质的特殊性,管道内部易产生腐蚀进而导致管道泄漏与破坏。例如,管道在输送压力物质时会受到内部物质运动造成的冲击和振动而引起管道的疲劳破坏,处理不当可能造成重大的安全事故和巨大的经济损失,因此对管道的动态监测和损伤识别尤为重要[1]。而管道的腐蚀和疲劳破坏会造成管道结构参数发生变化从而改变管道的动态特性[2-3]。因此,通过管道的动态监测发现管道异常的振动现象,对管道系统的维护与正常运行具有重要的现实意义。

目前,国内外学者在管道振动的动态监测领域开展了许多研究工作。高文傲[4]将光纤监测方法应用于管道泄漏研究,该方法可以有效监测管道泄漏对管壁振动的影响,且灵敏度高;李帅永等[5]利用接触式压电加速度传感器,根据管道泄漏声振动信号特性,将改进的经验小波变换应用于供水管道泄漏定位;荣锋等[6]针对金属物体微测量问题设计了基于电涡流传感器的测量系统,通过拟合的方法对传感器信号进行非线性补偿从而提高测量精度;陈佰成[7]利用加速度传感器测量导管的动态应力从而实现管道的动态监测。传统的结构振动测量通常采用接触式测量,会使轻质结构质量增加,降低实际测量结果的精度。随着机器视觉的发展,研究者们对结构的非接触式测量方法进行了大量的研究。Y.Fukuda[8]提出一种基于视觉的位移传感器监测动态响应系统,通过结构表面固有的特征实现动态载荷下结构位移的精准测量;T.Khuc[9]提出利用普通相机和计算机视觉技术的完全非接触式结构健康监测系统框架来获取结构的位移和振动;李东亮[10]利用单目视觉测量方法测量钢丝绳等横向振动测量难度较大的对象;王力超等[11]改进传统图像处理算法,提高了高速视觉的振动频率测量方法的实时性;S.Zhong[12]研究了适用于结构损伤检测的准光学相干振动测量系统,并分析了噪声对测量精度的影响。钟剑锋[13-16]提出一种基于二维视觉位感条纹的空间结构三维振动测量系统,但采用二维视觉需要采集较多的二维图像信息,对于成像相机性能要求和系统的图像处理能力要求较高,在实际的应用中存在一定的局限性。

为了改进二维视觉测量方法对设备要求较高的不足,针对管道振动监测问题,提出了一种基于线阵相机的管道二维振动测量方法。通过在管道表面设置正弦条纹图案,采用线阵相机获取管道表面的条纹图案,再采用提出的处理算法对一维条纹信号进行处理以获得管道本身的振动状态,为各类管道的动态监测提供一种新的方法。

1 基于线阵相机的管道二维振动监测系统

1.1 系统组成

基于线阵相机的管道二维振动监测系统如图1所示,该系统主要包括待测管道和线阵相机二维振动监测系统。规定沿成像光轴方向为X方向,垂直于成像光轴和管道轴线方向为Y方向,沿被测管道轴线方向为Z方向。测量前在被测管道表面粘贴正弦条纹,粘贴方式为条纹强度变化方向与管道圆周方向一致,如图1所示。调整相机位置及成像参数使正弦条纹清晰成像于线阵传感器上,成像条纹的密度信息会随着管道振动发生变化,以此实现管道二维振动信息编码。通过线阵相机实时采集条纹图案,并经数据线传输到电脑上进行储存;再采用提出的条纹图像处理方法对条纹信号进行处理与分析,提取管道的二维振动信息。

图1 基于线阵相机的管道二维振动监测系统图

1.2 X方向测量原理

管道表面粘贴的正弦条纹的实际宽度固定,根据管道振动和相机成像原理可得管道表面条纹在图像传感器上的成像条纹宽度将随管道X方向位置变化而变化,进而引起成像条纹密度发生变化,其测量原理如图2所示。以图2 “位置1”为初始参考位置,管道表面条纹经过成像透镜在相机内部图像传感器上形成如“成像1”所示的条纹,通过时频分析方法可得到条纹的频率变化曲线(即密度变化曲线),如图2中P0所示。因成像条纹密度被管道表面调制,因此可通过求取密度变化曲线的对称轴确定管道轴线位置,进而确定“成像1”条纹对称中心的条纹密度值。当管道沿着X方向产生Δx位移时,在成像平面上的“成像2”条纹宽度将发生变化,即成像条纹整体密度曲线及其对称中心处的条纹密度值也将变化,如图2中P(t)所示。所以通过求管道表面中心行条纹密度变化信息即可得到管道沿X方向的振动位移。假设t时刻被测管道在X方向上的振动位移为Δx时,根据文献[14]可得X方向的振动位移计算公式为

图2 动态监测系统X方向位移测量原理

(1)

式中:D为成像系统的成像物距;d0为被测管道初始位置;d(t)为管道发生振动位移为Δx(t)后的成像条纹对称中心的条纹密度值。

1.3 Y方向测量原理

如图3所示,当管道只在Y方向上有位移时,管道由初始参考“位置1”变化到“位置2”,此时对应的图像传感器上的成像条纹宽度不变,但成像条纹在成像传感器上发生了偏移。由图3中的成像关系可得,图像传感器Y方向上成像条纹密度曲线的对称中心偏移量和管道的振动位移之间关系为[14]

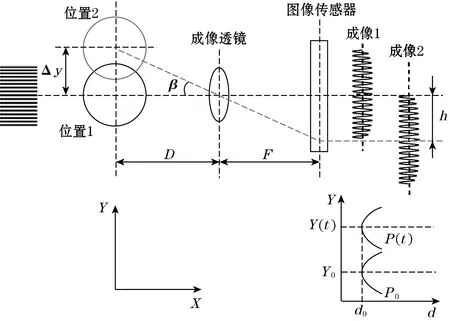
图3 动态监测系统Y方向位移测量原理

(2)

式中:F为成像透镜到图像传感器之间的像距;h(t)为图像传感器上成像条纹中心相对初始参考位置的偏移量;β(t)为初始参考“位置1”变化到“位置2”在成像透镜上的偏移角度;a为图像传感器上的像素点宽度;Δm(t)为t时刻条纹密度曲线的对称中心相对于初始参考位置的像素点坐标偏移量。

1.4 X方向和Y方向复合测量原理

如图4所示,管道同时具有X方向和Y方向的振动位移(复合运动),管道由参考 “位置1”变化到“位置2”,此时管道表面条纹在图像传感器上的宽度及位置都发生了变化,由图4中的成像关系可得,沿Y方向振动位移可表示为[14]

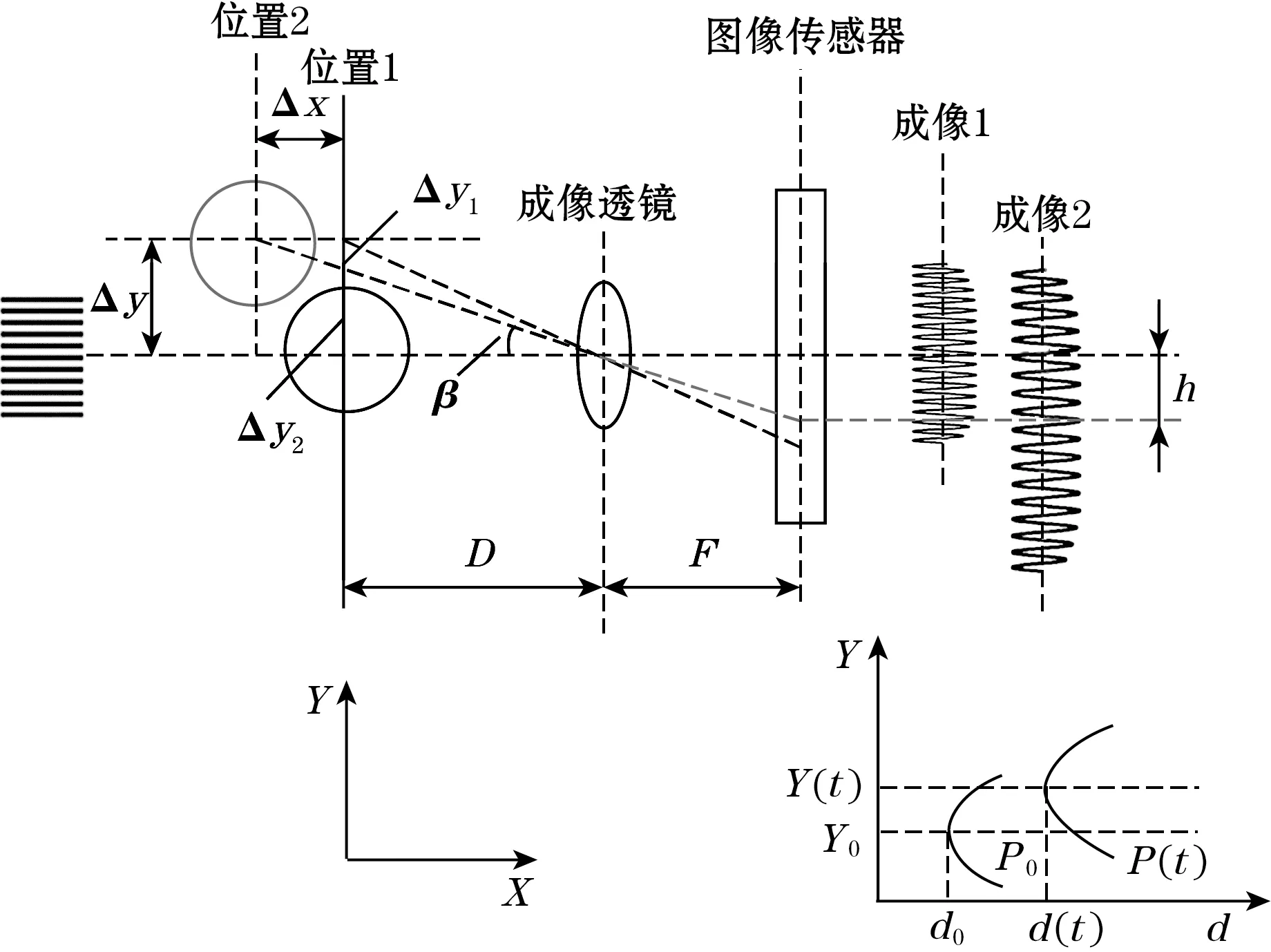
图4 X方向和Y方向同步测量原理

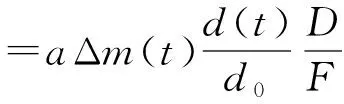
(3)

条纹图像的缩放比例系数S可由式(4)计算得到

(4)

式中:D为成像物距;F为像距;L为图像传感器上条纹沿管道圆周方向的实际宽度;A为“位置1”时条纹中心行覆盖的像素点的个数。

将条纹图像的缩放比例系数S带入式(3)可得到管道Y方向的振动位移:

(5)

由式(1)和式(5)可知,准确得到管道振动位移的关键在于精确计算t时刻条纹密度曲线对称中心相对于初始参考位置的像素点坐标偏移量Δm(t)与对称中心条纹的密度值d(t)。因此,成像正弦条纹密度曲线的准确提取至关重要,其计算原理及步骤如图5所示。

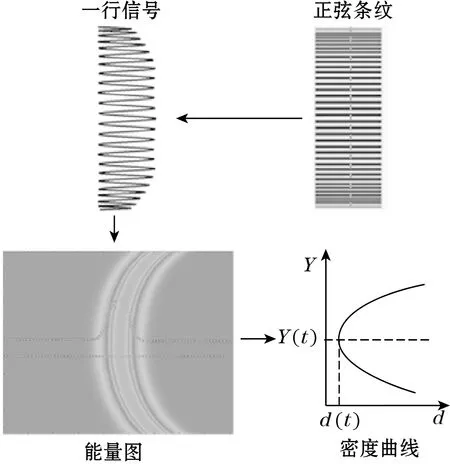
图5 条纹密度曲线提取原理

线阵相机每个采样时刻获取管道表面条纹中一行的条纹信号,然后采用时频分析方法得到不同成像位置条纹信号的时频能量图,再采用能量重心校正法[17]对能量图中每行频谱的能量重心进行校正,最终得到每一时刻成像条纹的密度变化曲线。密度变化曲线通过二次函数进行拟合,即可求得密度变化曲线对称中心线的坐标变化及对称中心坐标的条纹密度值变化,将对应值带入式(1)和式(5)即可得到管道X方向和Y方向的振动位移。

2 模拟实验与分析

为验证该测量方法的可行性与准确性,通过 SolidWorks软件的运动仿真和成像模块进行模拟实验。根据实验管道的具体参数对模型进行参数化建模,在管道表面粘贴正弦条纹,并设置6种不同组合的振动模式,振动位移函数分别如式(6)～式(11)所示:

(6)

(7)

(8)

(9)

(10)

(11)

在SolidWorks仿真模型的X方向和Y方向添加线性马达并将振动位移函数式(6)～式(11)分别作用到马达上以模拟管道不同模式下的周向振动,再利用软件自带的虚拟相机,设置准确的图像采集位置,在管道振动过程中对管道表面粘贴条纹的振动进行实时监测。模拟中成像条纹的分辨率设置为1 pixel×2 048 pixel,图片的采样频率为100 fps。依次得到仅单方向和复合振动位移函数下的成像条纹序列,再利用已知的条纹处理算法进行图像处理得到结果。

为了验证本方法对小振幅和大振幅振动测量的效果,首先采用式(6)和式(7)的振动函数模拟了管道只在X方向和Y方向有小位移振动的情况,结果如图6所示。由图6可知,在单方向上模拟测量结果与实际管道设置的振动位移一致。随后采用式(8)和式(9)的振动函数模拟了管道只在X方向和Y方向有大位移振动的情况,结果如图7所示。由仿真结果可知,所提出的位移提取算法可精确地提取管道周向二维振动位移,与标准振动位移曲线几乎一致。

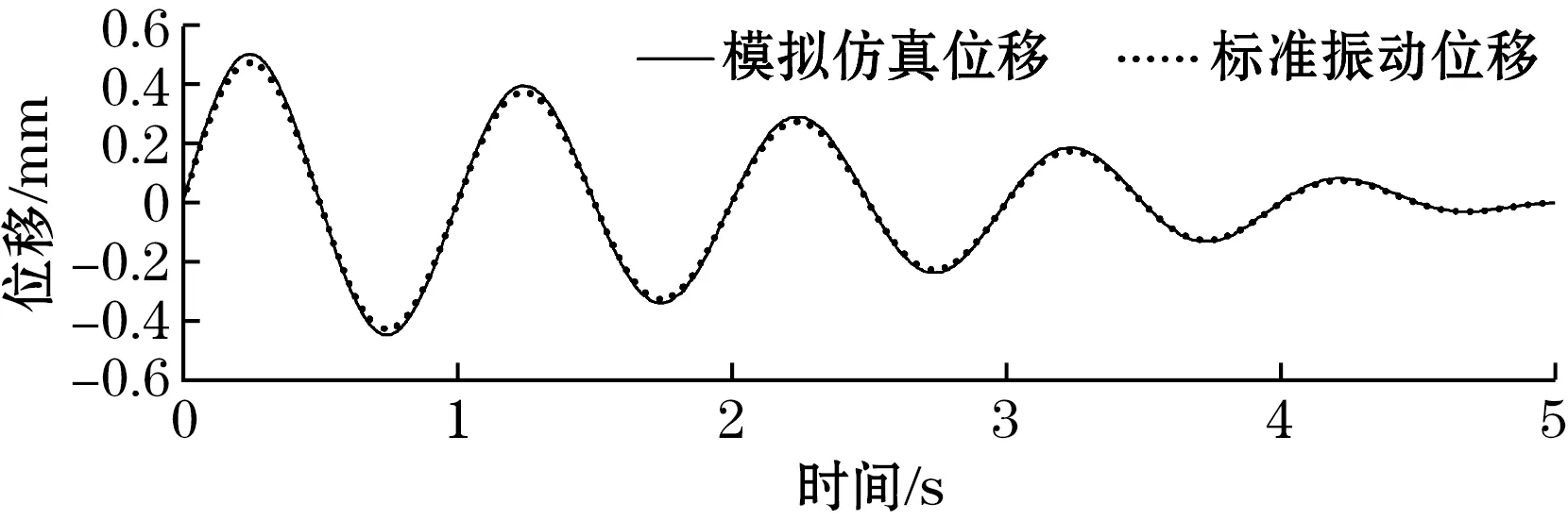
(a)仅X方向振动

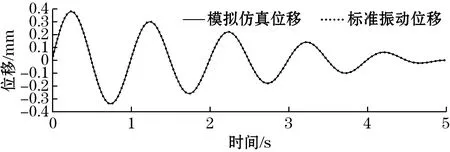
(b)仅Y方向振动图6 单方向小位移振动测量

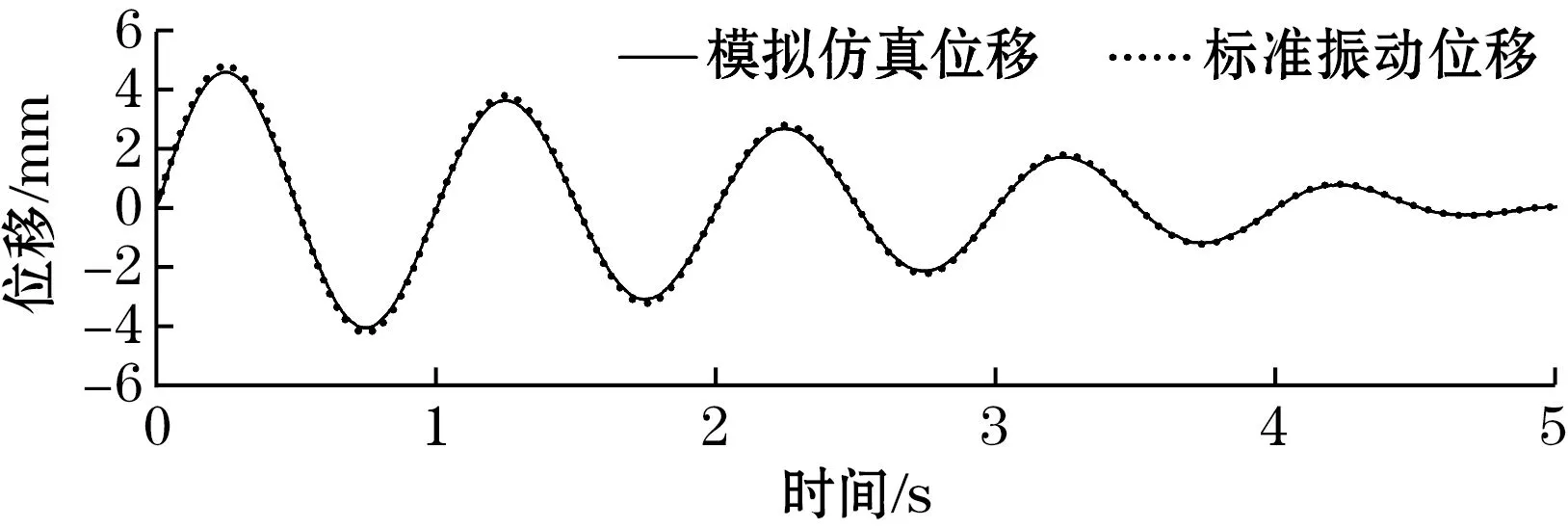
(a)仅X方向振动

(b)仅Y方向振动图7 单方向大位移振动测量

实际管道的振动大多是X和Y2个方向同时振动(复合运动),为验证管道在复合运动中各方向的振动是否会互相影响,采用式(10)和式(11)模拟了小幅值与大幅值的复合运动,模拟的条纹序列处理结果如图8所示。由结果可知,通过条纹序列变化规律得到的管道振动位移曲线和仿真设置的振动位移结果吻合。因此,提出的测量方法和位移提取算法可以较好地分离出不同方向的位移信息而不互相影响。模拟实验结果也验证了此测量方法在大振幅范围内具有较好的测量性能。

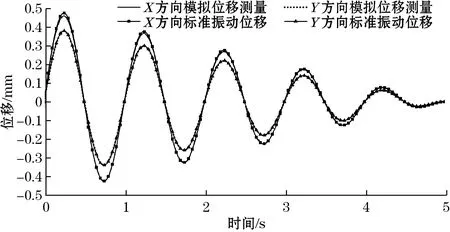
(a)小位移复合运动

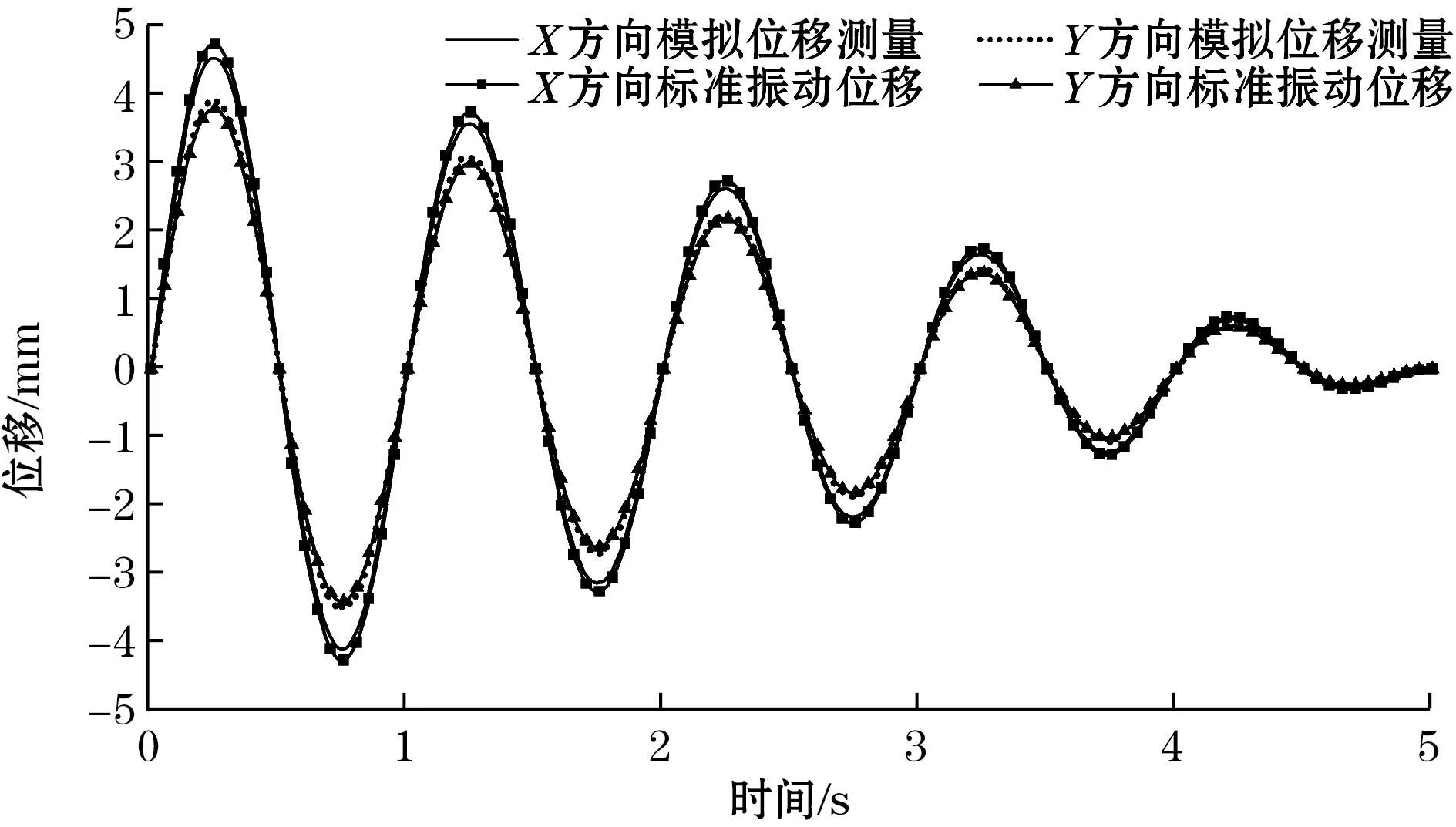
(b)大位移复合运动图8 复合运动振动位移测量

本文提出的测量系统主要是由正弦条纹和线阵相机组成。管道的振动位移是从条纹密度变化信息获得。为了得到准确的位移测量结果,就要精确得到成像条纹的密度曲线。在实际测量中,影响成像条纹密度信息获取的因素主要有条纹本身的质量、光照条件、条纹周期数及相机成像传感器的分辨率等,条纹本身的质量、光照条件和成像传感器的成像性能决定了成像条纹的信噪比。为了研究信噪比对测量精度的影响,在复合运动下,分别研究了条纹信噪比为0、10、20、30、40、50、60 dB条件下不同位移振动情况下的标准位移差,结果如图9所示。当成像条纹信噪比为0 dB时,X方向和Y方向测量的标准位移差与实际测量的位移所得偏差量为30%,对测量精度带来较大影响。但随着条纹信噪比的提高,测量精度也逐渐提高,当条纹信噪比大于30 dB以后可达到较高的测量精度。因此,在实际测量过程中需要保证条纹图案本身质量以及在测量过程中的光照条件,以保证测量的图片具有良好的信噪比。在光线较弱条件下可通过增加外部光源来改善光照条件,以保证系统的测量性能。

(a)不同信噪比下小位移振动标准位移差

(b)不同信噪比下大位移振动标准位移差图9 不同信噪比振动位移标准差对比结果

为研究不同初始条纹周期数对测量精度的影响,在SolidWorks模拟中,通过更改管道表面粘贴的条纹密度的方法验证小位移复合运动的振动条件下条纹密度对测量结果的影响。分别在待测管道表面粘贴每100 mm分别有21、31、41、51、61、71、81、91、101周期的条纹图案,不同条纹周期数下测量位移和实际位移之间的标准差结果如图10所示。可见当条纹密度为每100 mm有21周期时,X方向振动位移标准差为0.016 3 mm,Y方向振动位移标准差为0.016 4 mm,此时测量位移精度较低,但随着条纹周期数的提高,模拟实验结果的位移测量精度也相对提高,当条纹密度为每100 mm有71周期时,精度最高。但是进一步提高条纹密度时位移标准差反而有增大趋势,因为密度过高时条纹信号的采样受到传感器像素分辨率的限制。可见在实际测量过程中,在其他条件不变的情况下,适当地提高条纹的密度有利于提高测量精度。

图10 不同条纹周期数振动位移标准差对比结果

3 实验及分析

为了验证基于线阵相机的管道二维振动测量方法的可行性与准确性,搭建并设计了如图11(a)所示的管道振动实验测量系统。将长120 mm、直径为20 mm的PVC管道固定在激振器输出端,在距离管道固定端80 mm的位置粘贴正弦条纹图案。信号发生器产生的控制信号通过功率放大器放大后输入激振器中以得到理想的振动信号,如图11(b)所示。作为对比实验,采用电涡流传感器(型号为5E102,量程为2 mm,量程中点为1.5 mm)对管道进行同步测量。因PVC管道为非金属材质且管道在振动过程中固定端的振动和管道相同,因此采用电涡流传感器测量金属固定座振动来间接测量管道的振动,安装方式如图11(c)所示。实验中线阵相机采集图片的成像分辨率为1 pixel×2 048 pixel,曝光时间为997 μs,采样帧率为1 000 fps。为更好地进行时域位移的对比,将电涡流传感器的采样频率也设置为1 000 Hz。管道表面条纹的成像条纹的序列图如图11(d)所示,利用提出的信号处理方法,得到管道X方向振动信息。为提高条纹的成像质量,测量中采用外部光源改善环境光照条件。由于激振器只能提供1个方向的正弦振动,而管道的实际振动不仅有X方向振动,还会有Y方向振动,因此将激振器旋转90°之后进行Y方向振动测量,如图11(e)所示。Y方向振动测量实验中仅改变了管道振动的方向,相机成像参数均与X方向振动测量实验相同。

图11 管道振动测量实验装置图

实验过程中设置激振器输出频率为10 Hz的正弦振动使管道发生振动,采用提出的测量方法与电涡流传感器测量方式进行同步测量,得到如图12所示的单方向振动位移曲线。为了清晰表达测量结果,仅显示1 s内的振动位移,由振动位移曲线对比发现线阵相机的测量结果与电涡流传感器测量结果几乎一致,但存在微小误差,该误差是由条纹质量导致,若要减小误差可以通过提高条纹图案本身的质量以提高测量精度。振动曲线有微小的相位差是由于测量过程中无法保证两种测量方式完全同步开始,从振动位移的振幅和振动周期可以确定2种测量结果几乎一致。

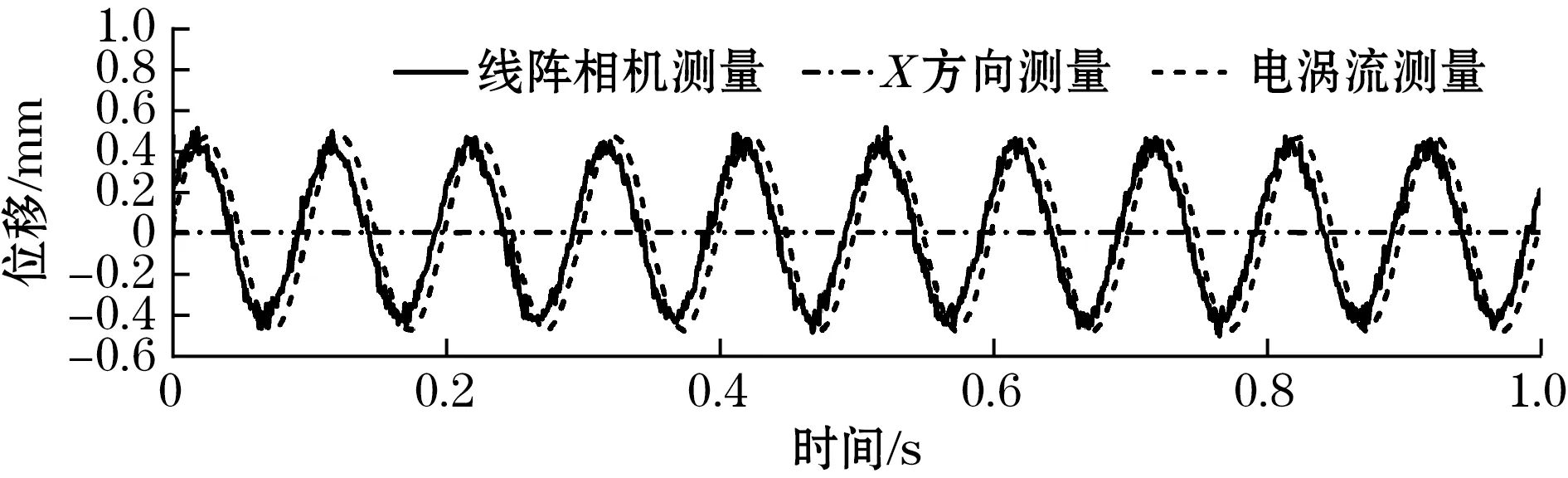
(a)仅X方向振动

(b)仅Y方向振动图12 电涡流传感器量程内单方向位移测量结果对比

电涡流传感器的量程范围为0.5～2.5 mm,且量程中点为1.5 mm,安装时既要考虑电涡流传感器金属探头与被测物体的距离,又要考虑物体在运动过程中与探头是否会发生碰撞,若安装距离不当则会出现采集信号截断问题。实验中将激振器输出振动幅值增大,得到如图13所示的振动位移曲线。可见,电涡流传感器采集的振动信号出现截断而非正弦形状。因此,在实际测量过程中若选用电涡流传感器测量物体振动位移,需要根据测量的实际需求来选择适合量程的电涡流传感器。而本文提出的基于线阵相机的管道二维动态测量方法对被测管道的材质没有要求,可适用于更大振幅的振动测量,且测量时安装更加快捷、方便。

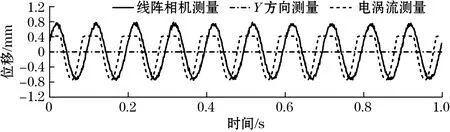
(a)仅X方向振动

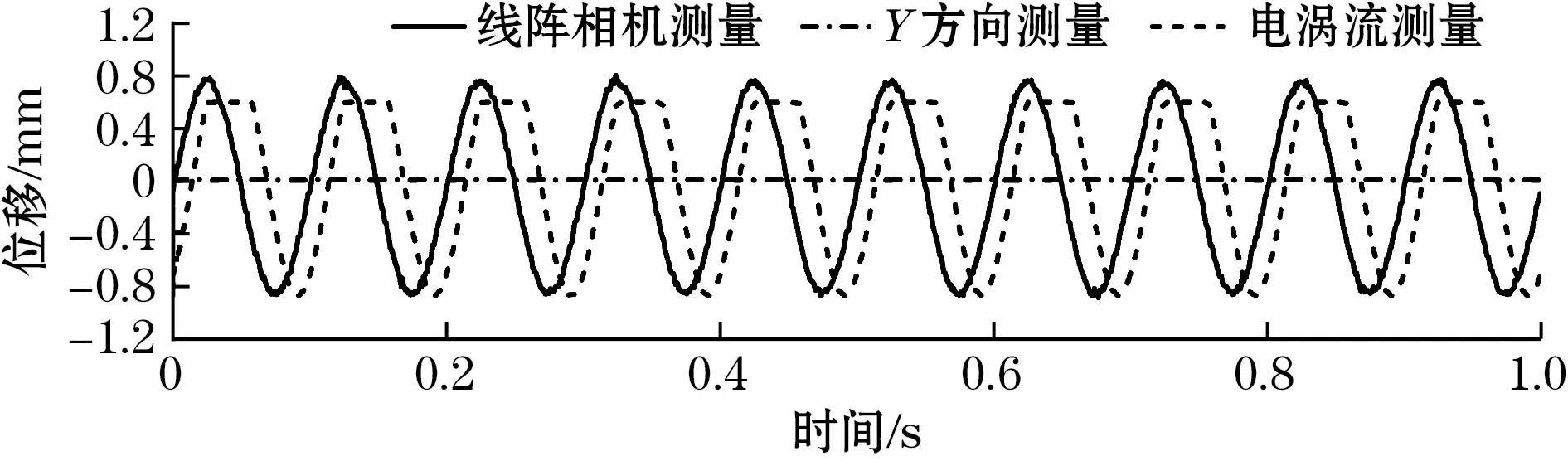
(b)仅Y方向振动图13 电涡流传感器量程外单方向位移测量结果对比

上述实验证明提出的测量方法可实现管道周向2个方向振动位移的分别测量,但实际管道的振动以2个方向的复合运动为主,因此对金属管道的复合运动进行实验测量,如图14(a)所示。测量对象为一根长1 000 mm、直径为20 mm的金属管道,采用一端固定的方式固定管道,在距离管道固定端500 mm的位置粘贴一张宽度为18 mm的正弦条纹图案,如图14(b)所示。作为对比实验,在管道条纹处安装电涡流传感器,安装方式如图14(c)所示,相机型号与电涡流传感器型号及测量参数与单方向测量实验时一致。

图14 管道复合振动测量图

管道复合振动位移测量结果如图15和图16所示。可知线阵相机的测量结果与电涡流传感器测量结果一致,证明2种方法都能较好地测量管道复合振动位移。为验证本文提出的测量方法在频域测量结果上的准确程度,将线阵相机的频域测量结果偏置200 dB,与电涡流传感器的频域测量结果对比如图17所示。可知2种测量方法都得到管道在振动过程中的多阶共振频率。因此提出的测量方法可实现管道周向二维振动的同步测量,可为管道的异常振动监测及故障诊断分析提供新的测量方法。

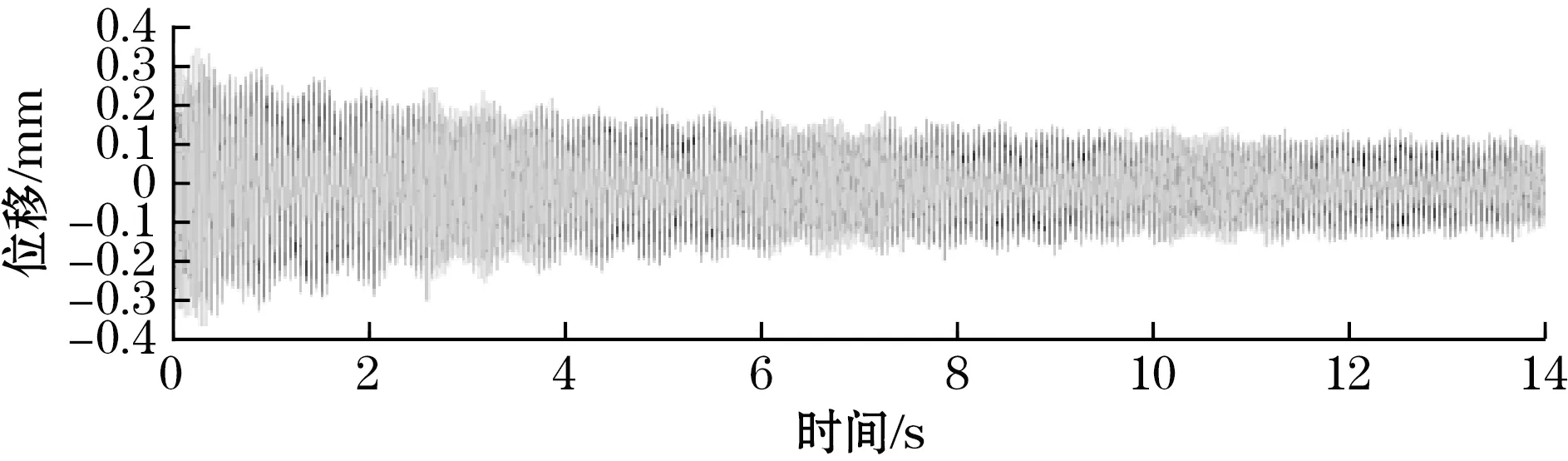
(a)线阵相机测量管道X方向振动位移曲线

(a)线阵相机测量管道Y方向振动位移曲线

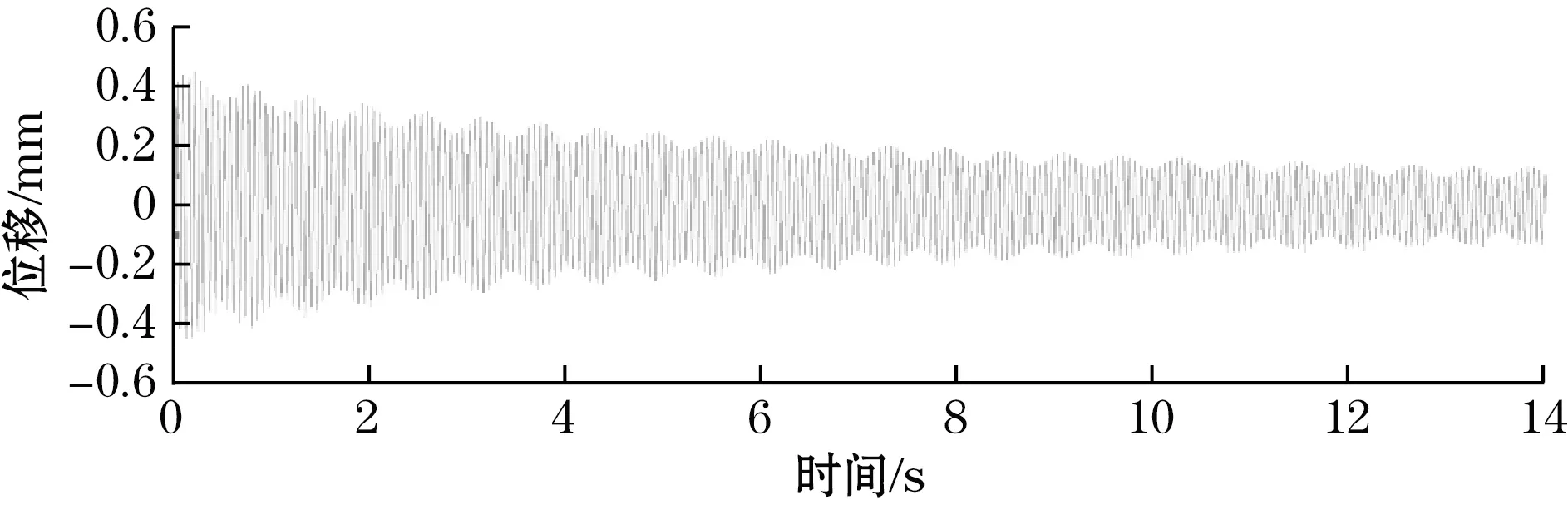
(b)电涡流传感器测量管道Y方向振动位移曲线图16 线阵相机与电涡流传感器Y方向振动位移测量对比

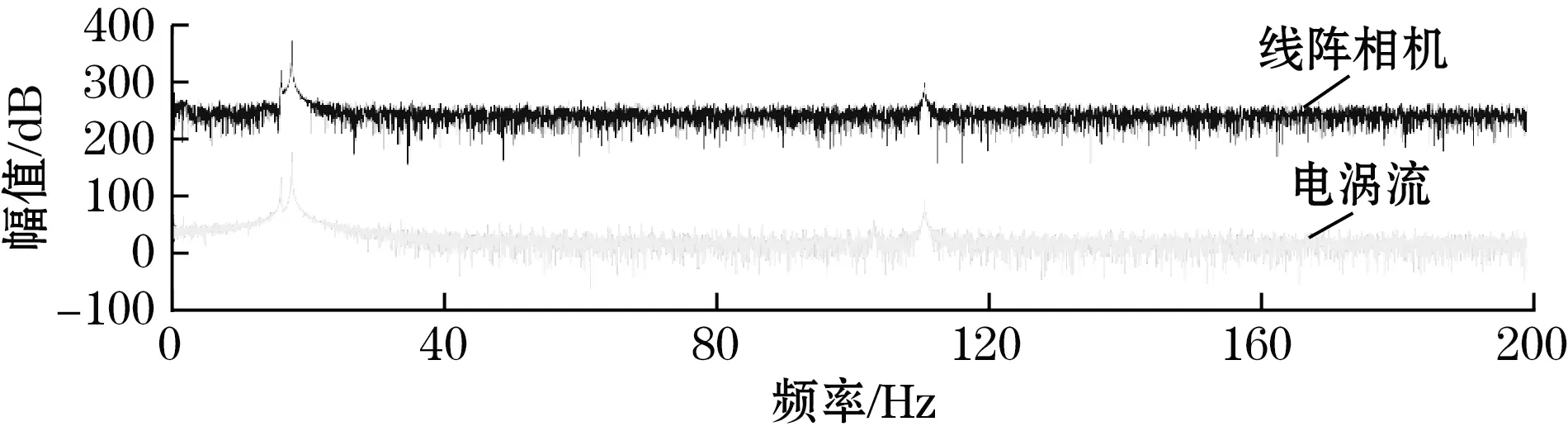
(a)线阵相机与电涡流传感器测量X方向位移频域结果

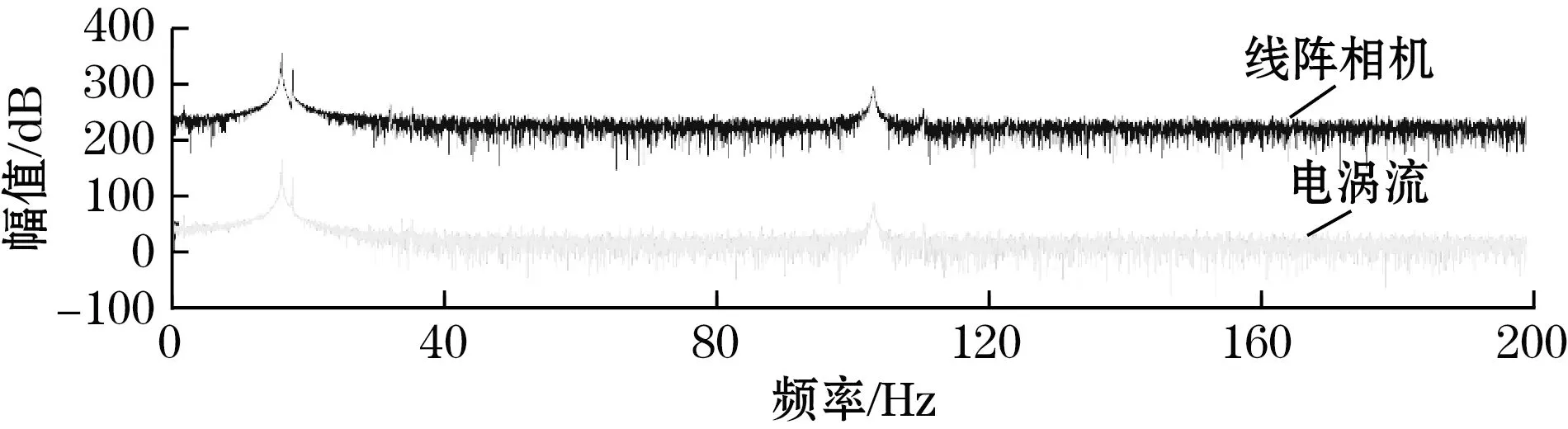
(b)线阵相机与电涡流传感器测量Y方向位移频域结果图17 线阵相机与电涡流传感器频域测量对比

4 结束语

为了实现管道的振动测量,提出一种基于线阵相机和正弦条纹的管道周向二维振动测量方法。利用线阵相机对振动管道表面的编码条纹信号进行采集处理即可实现管道周向二维振动的测量与分析。利用SolidWorks建立二维振动模拟测量模型,模拟结果表明,在成像分辨率一定情况下,提出方法的测量精度随被测条纹信噪比提高而提升;在可清晰拍摄条纹前提下,提高条纹密度也可提高位移测量分辨率。模拟与对比实验结果表明:本文提出的基于线阵相机的管道二维振动测量方法可以实现10 mm范围内管道周向二维振动同步、准确的测量,位移测量精度优于10 μm。

与传统的电涡流测量系统和接触式加速度传感器测量系统相比,提出的一维线阵相机监测系统在测量系统的成本和测量便捷性、效率、量程范围等方面有一定的优势,且适用于轻质、非金属、大位移等测量场合,具有一定的推广应用价值。