电磁MEMS微镜贴片封装残余应力测试与特性研究

刘春程,方肖勇,李修远,吴佳豪,张文明

(1.上海交通大学机械与动力工程学院,上海 200240;2.华为技术有限公司,广东深圳 518000)

0 引言

以微机电系统(micro electromechanical system,MEMS) 微镜为核心光学扫描器件的半固态激光雷达,具有成本低、体积小、产能高等优点[1-2]。MEMS微镜的工作稳定性时刻受到车载环境的影响,微镜的失效将导致MEMS激光雷达的性能下降甚至无法工作,因此微镜的可靠性成为制约MEMS激光雷达产业化的关键问题。

封装残余应力会严重影响MEMS器件性能与寿命[3-4],因此分析与优化封装残余应力对于提升MEMS微镜芯片的可靠性具有重要意义。层合结构因材料热膨胀系数失配而产生挠曲变形和热应力[5],影响器件的工作性能。研究表明,结构优化设计是降低封装残余应力的有效途径[5-7]。Z.Chen等[6]利用环形结构隔离了内部器件99.7%的热应力。此外,许多学者研究了封装残余应力的影响规律[8-12]。X.Zhang等[12]研究了三轴加速度计温度影响下的挠曲变形、封装应力以及输出偏移特性。C.L.Lu和M.K.Yeh[8]以及Z.Zhang等[9]报道了粘接剂的杨氏模量、厚度等参数对压力传感器芯片封装热应力的影响。李平等[11]研究了基板厚度、温度、胶水热膨胀系数等因素对MEMS高g加速度传感器封装热应力的影响规律。MEMS封装残余应力研究的对象多为微加速度计或MEMS压力传感器等应力敏感器件[9,13],然而,关于MEMS微镜的残余应力相关研究报道较少。目前,针对电磁MEMS微镜的残余应力表征或测试方法具有多样化,其中光学方法如拉曼光谱法[14]需要使用光谱仪进行测试;接触式测量方法易损伤器件;利用共振检测残余应力的方法[15-18]具有无接触、非破坏性等优点,因此本文基于此方法对电磁微镜的残余应力进行表征。

本文旨在探究MEMS微镜贴片封装残余应力的影响因素及其变化规律,为微镜贴片封装优化设计提供技术支持;建立微镜谐振频率特性与残余应力间的关系,为电磁MEMS微镜残余应力表征提供理论依据。本文首先基于层合梁热变形理论,研究MEMS微镜贴片封装所致热变形。结合仿真分析,给出基底厚度、基底模量、胶水厚度及模量、温度变化、热膨胀系数、粘接方式等因素对残余应力的影响规律;其次,阐述微镜Piston模态谐振频率漂移特性与轴向残余应力间的解析关系;最后,制备不同贴片参数的MEMS微镜芯片贴片样品,测试其Piston模态特征频率偏移程度,并使用第2节中的方法评估样品残余应力。

1 微镜贴片封装残余应力建模

本节围绕微镜贴片封装过程中引入的残余应力与挠曲变形展开理论与仿真研究。基于Suhir层合梁理论,探究了多种贴片参数影响下芯片最大挠曲变形,并结合有限元分析,验证所建模型有效性。

1.1 理论模型

图1(a)为本文研究的单轴MEMS微镜芯片,采用电磁式驱动,主要结构包括反射镜、镜轴、平衡框、金属线圈和背部支撑梁。微镜的一阶模态为工作模态,谐振频率约为268 Hz,如图1(b) 所示。

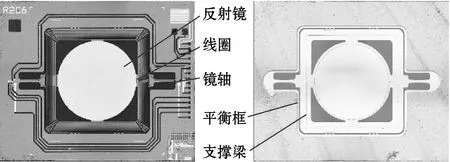
(a)MEMS微镜显微成像

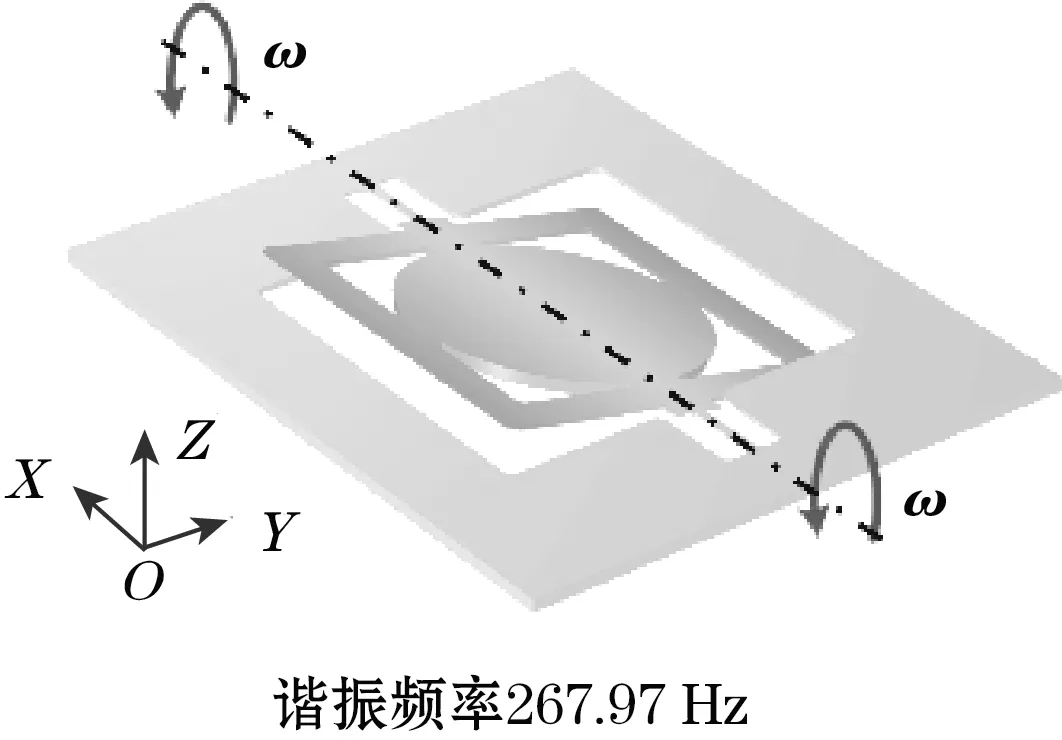
(b)MEMS微镜扭转模态振型图1 MEMS微镜芯片显微成像与扭转模态振型

层合结构由上至下分别为芯片、胶水和基底,贴片过程中,温度由胶水热固化温度降低至室温,层合结构因热膨胀系数失配而产生挠曲变形。由于结构的长、宽远大于厚度,可等效为矩形薄板结构,其宽度的横截面,如图2所示。

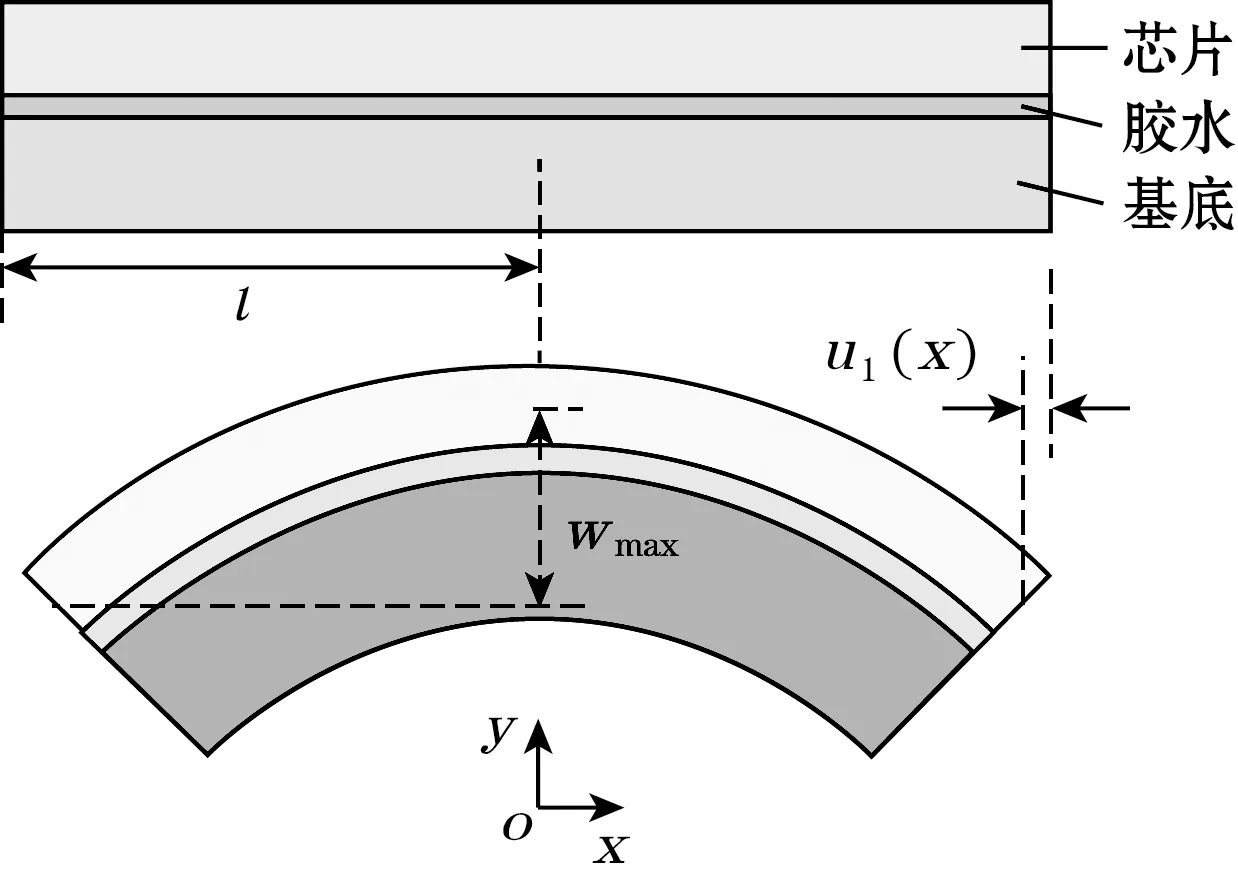
图2 贴片微镜平面理论模型示意图

在模型中,可以假设胶水完全粘接,忽略芯片和基底镂空结构带来的影响,仅考虑重合部分形变,忽略胶水热膨胀对层合结构的影响,仅考虑胶水剪切变形。基于Suhir理论[19-20]研究层合梁结构热变形,理论模型参数见表1。

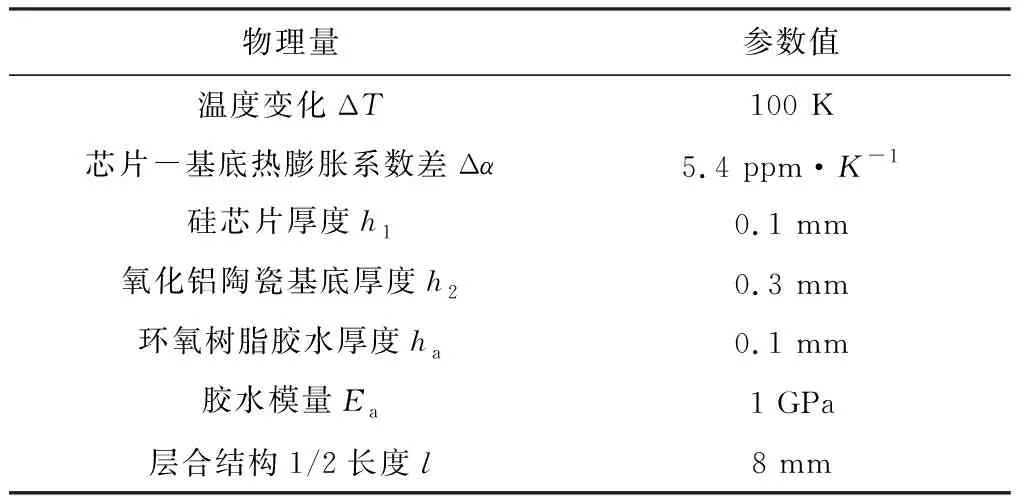
表1 理论模型参数表

假设层合结构变形沿y轴对称,则层合梁中心处,有x=0,此时得到最大挠曲变形vmax为[19]

(1)

式中:h为层合结构整体厚度,mm;Δα为芯片与基底之间的热膨胀系数差,ppm·K-1;ΔT为胶水热固化前后温度变化,K;γ为根据层合结构变形协调关系推导得到的参数[19],

(2)

式中:h1为芯片厚度,mm;h2为基底厚度,mm;l为平面层合结构一半长度,mm;D1为芯片抗弯刚度;D2为基底抗弯刚度;D为芯片与基底抗弯刚度之和:

D=D1+D2

(3)

(4)

式中:E1为芯片模量,GPa;ν1为芯片泊松比,ν1=0.28;E2为基底模量,GPa;ν2为基底泊松比,ν2=0.26。

(5)

式中:ha为胶水厚度,mm;Ea为胶水模量,GPa;νa为胶水泊松比,νa=0.44;κ为芯片、基底和胶水界面顺应系数之和[19];式中第一项表示芯片的剪切柔度;第二项和第三项分别代表基底和胶水的剪切柔度,其中定义K为

(6)

由式(1)可得,层合结构的最大挠度与温度、基底材料,胶水材料等因素有关,下节将进一步探究各贴片参数的影响规律。

1.2 参数影响与有限元分析

在有限元中建立微镜芯片三维贴片模型和平面层合梁模型,从三维和二维2个维度上探究微镜贴片残余应力变化规律,并与1.1节中的理论模型进行比较,对理论模型进行评估。

有限元模拟芯片封装贴片过程中从固化温度冷却至室温的热变形与热应力,如图3所示。图3(c)中,微镜的挠曲变形从中心至四边逐渐减小,中心处最大挠度可达55 μm。平面层合模型如图3(d)、图3(e)所示,采用平面应变假设,以层合结构的最大挠度作为因变量。将二维和三维模型的最大挠度进行比较时,仅考虑沿长边方向弯曲。表2给出了贴片微镜热变形的仿真模型参数。

(a)贴片微镜三维模型 (b)贴片微镜三维爆炸图 (c)贴片微镜三维热变形有限元

(d)平面有限元网格 (e)平面模型Von Mises应力图3 贴片微镜三维、二维模型及有限元仿真

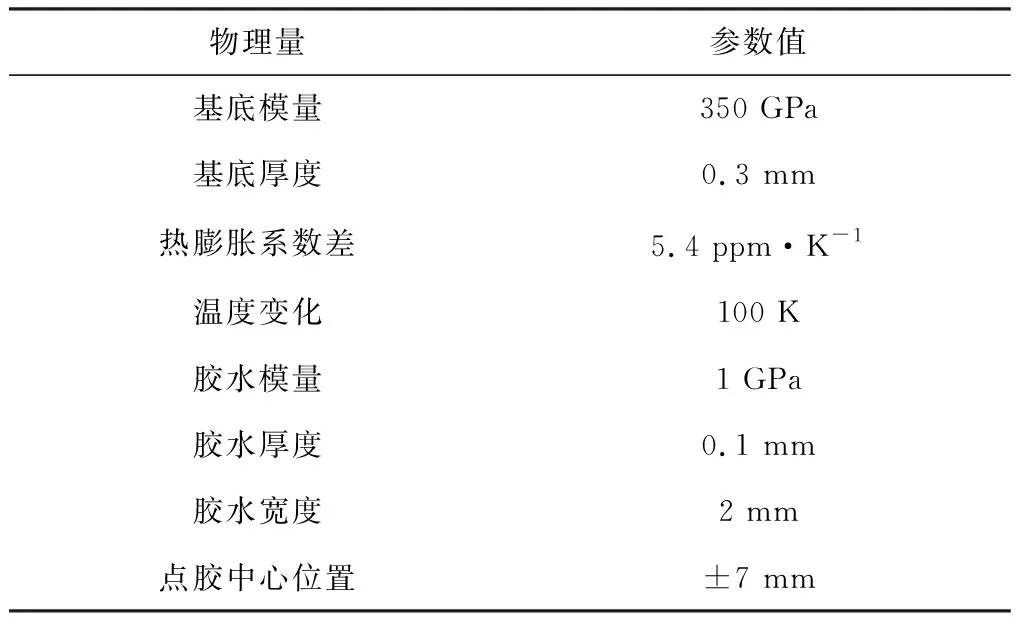
表2 仿真模型参数表

1.2.1 封装材料物理参数影响

封装材料物理参数如基底模量、基底厚度、胶水模量和胶水厚度对层合结构热变形影响如图4(a)～图4(d) 所示,图中纵轴为层合结构最大挠度,横轴变量为所探究贴片参数。

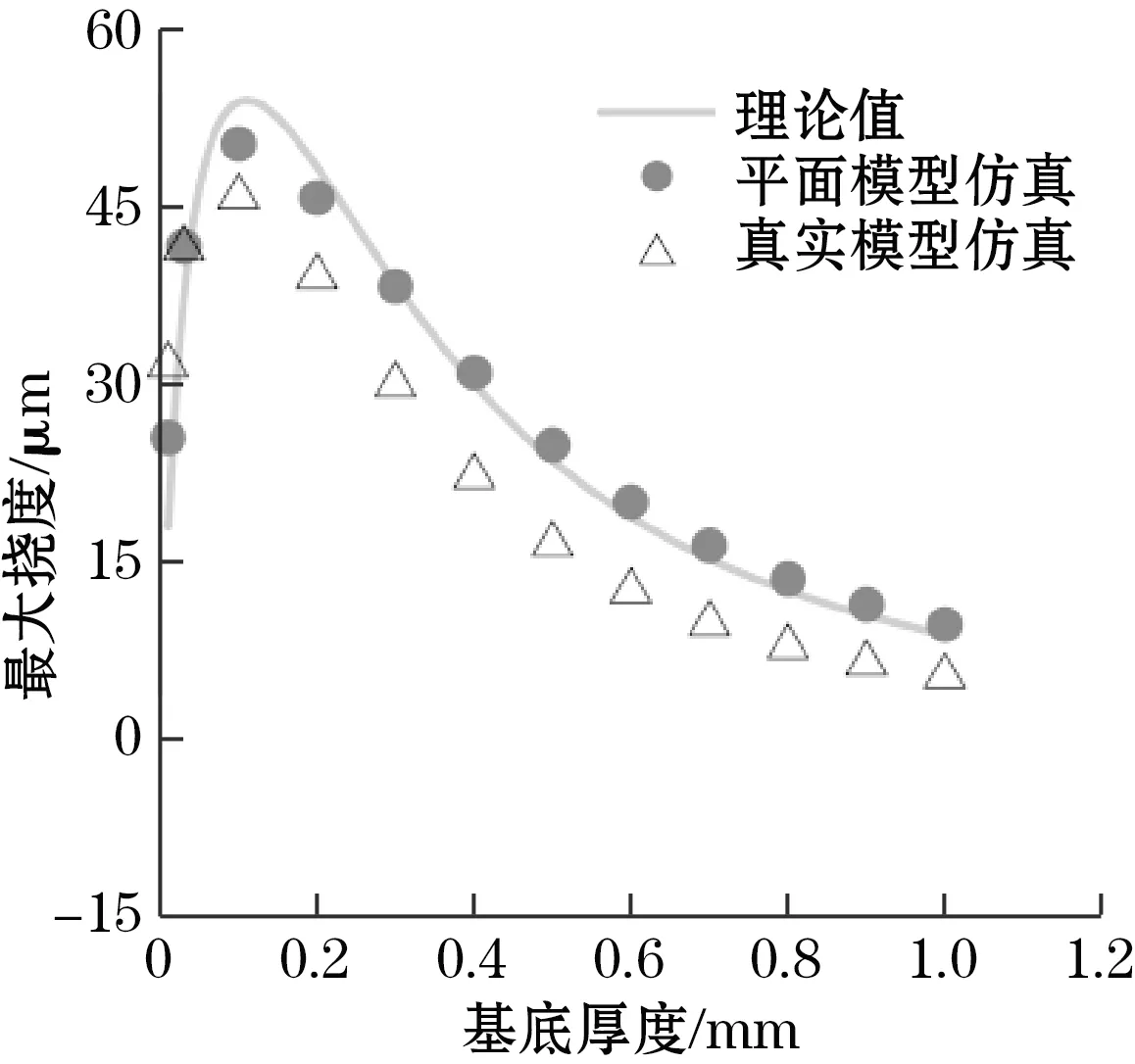
(b)芯片最大挠曲变形与基底厚度关系

(c)芯片最大挠曲变形与胶水模量关系

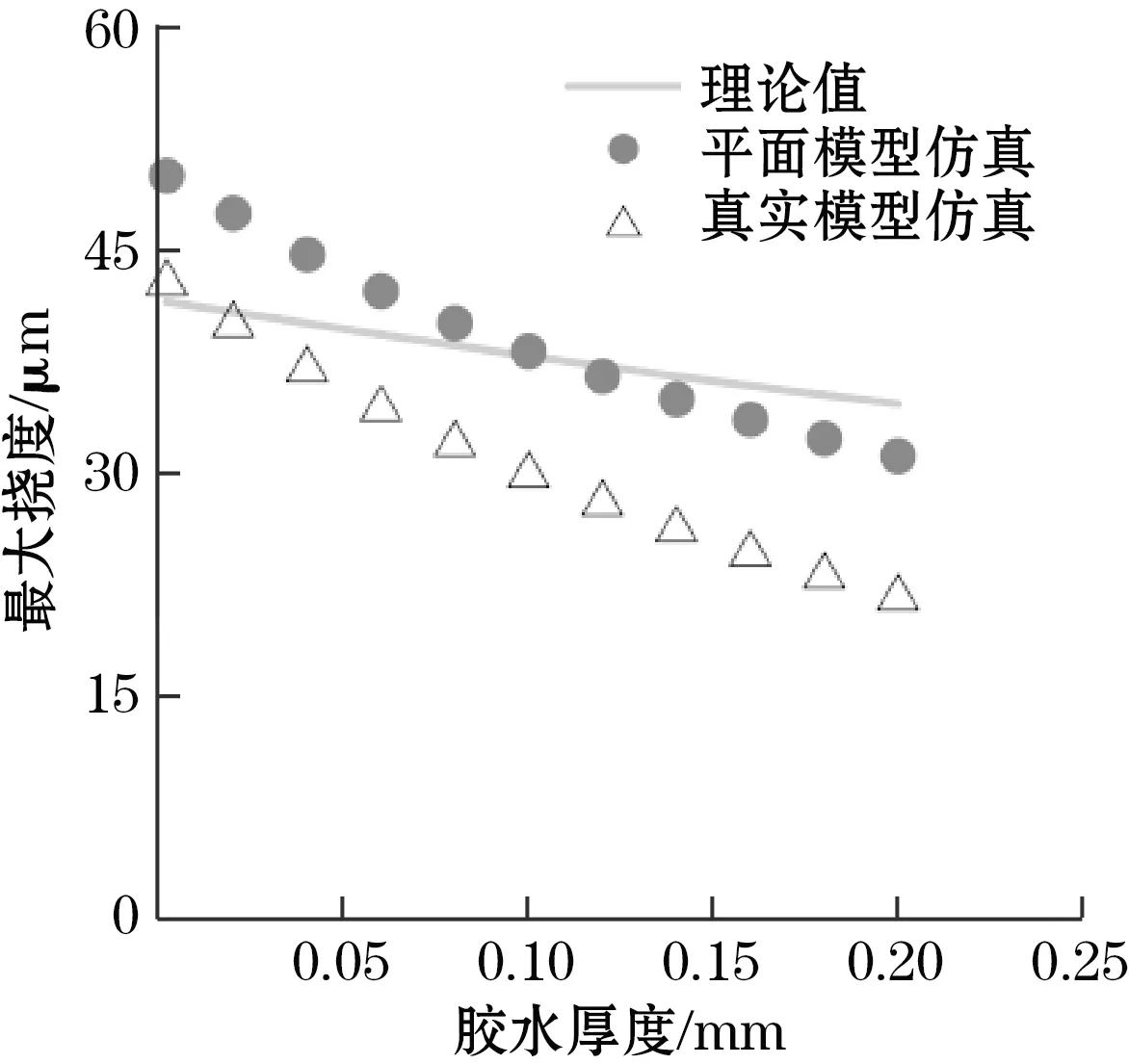
(d)芯片最大挠曲变形与最大挠度关系图4 芯片最大挠曲变形与封装材料物理参数关系

从热变形结果来看,理论模型与二维、三维有限元模型整体趋势一致,而数值上三维模型普遍偏小,差异主要来源于理论模型忽略了镜面与镜轴的抗弯刚度差异,即镜面与镜轴产生相同程度的挠度弯曲,而从图3(c)的三维热变形仿真结果可知,镜面部分的抗弯刚度远大于镜轴,几乎不发生挠曲变形。理论上,通过修正抗弯刚度,由于未考虑截面变化造成的挠度差异可以被完全消除,因此认为该理论模型可以揭示影响贴片热变形的变化规律。

图4(a)中,随基底模量增大,层合结构最大挠度呈先增加后减小的变化趋势,其中,当基底模量由10 GPa增大到100 GPa时,理论模型所得的层合结构最大挠度从22 μm增加至41 μm;当基底模量继续增至1 000 GPa时,最大挠度则下降至31 μm。

图4(b)中,随着基底厚度增加,层合结构的最大挠度呈先增大后降低的趋势。其中,当基底厚度从0.01 mm增至0.12 mm时,理论模型最大挠度从18 μm上升至54 μm;当基底模量继续增加至1 mm时,最大挠度降至9 μm。

图4(c)中,随着胶水模量增大,层合结构的最大挠度增大至一定程度不再发生变化。其中,当胶水模量增加至100 MPa后,理论模型的最大挠度基本保持在42 μm不变。图4(d)中,随着胶水厚度增加,最大挠度呈现单调下降趋势。其中,当胶水厚度由0.01 mm增加至0.2 mm后,理论模型的最大挠度由41 μm下降至35μm。

基底的厚度与模量影响了基底的抗弯刚度。分析可知,在基底抗弯刚度足够大的情况下,芯片不易发生翘曲;芯片抗弯刚度相对基底足够大时,芯片翘曲同样不易发生;而当基底抗弯刚度与芯片接近时,芯片挠曲程度达到最大。此外,实际应用中,胶水模量大多在0.1 ～ 1 GPa范围内,因此选取模量较小、厚度较大的胶水可以改善芯片的挠曲变形。

1.2.2 贴片工艺参数影响

通过上节分析可知,基底厚度是影响热变形的重要因素。本节中通过二维有限元仿真,进一步探究贴片工艺参数如芯片与基底间热膨胀系数差、温度变化、点胶中心位置、点胶宽度、胶水溢出等对层合结构最大挠度的影响规律,如图5(a)～ 图5(e)所示。

(a)芯片最大挠曲变形与热膨胀系数差关系

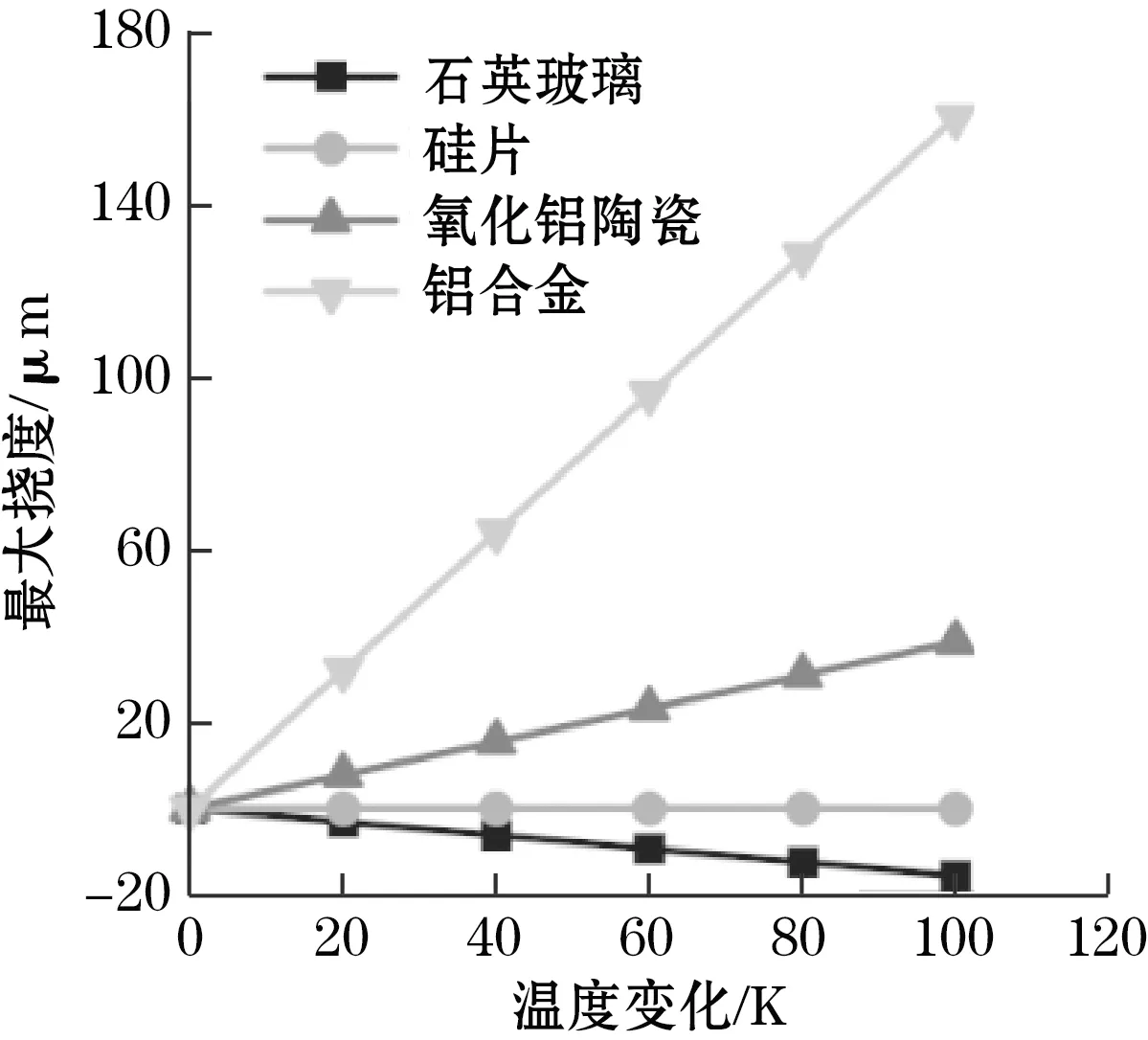
(b)芯片最大挠曲变形与温度变化关系

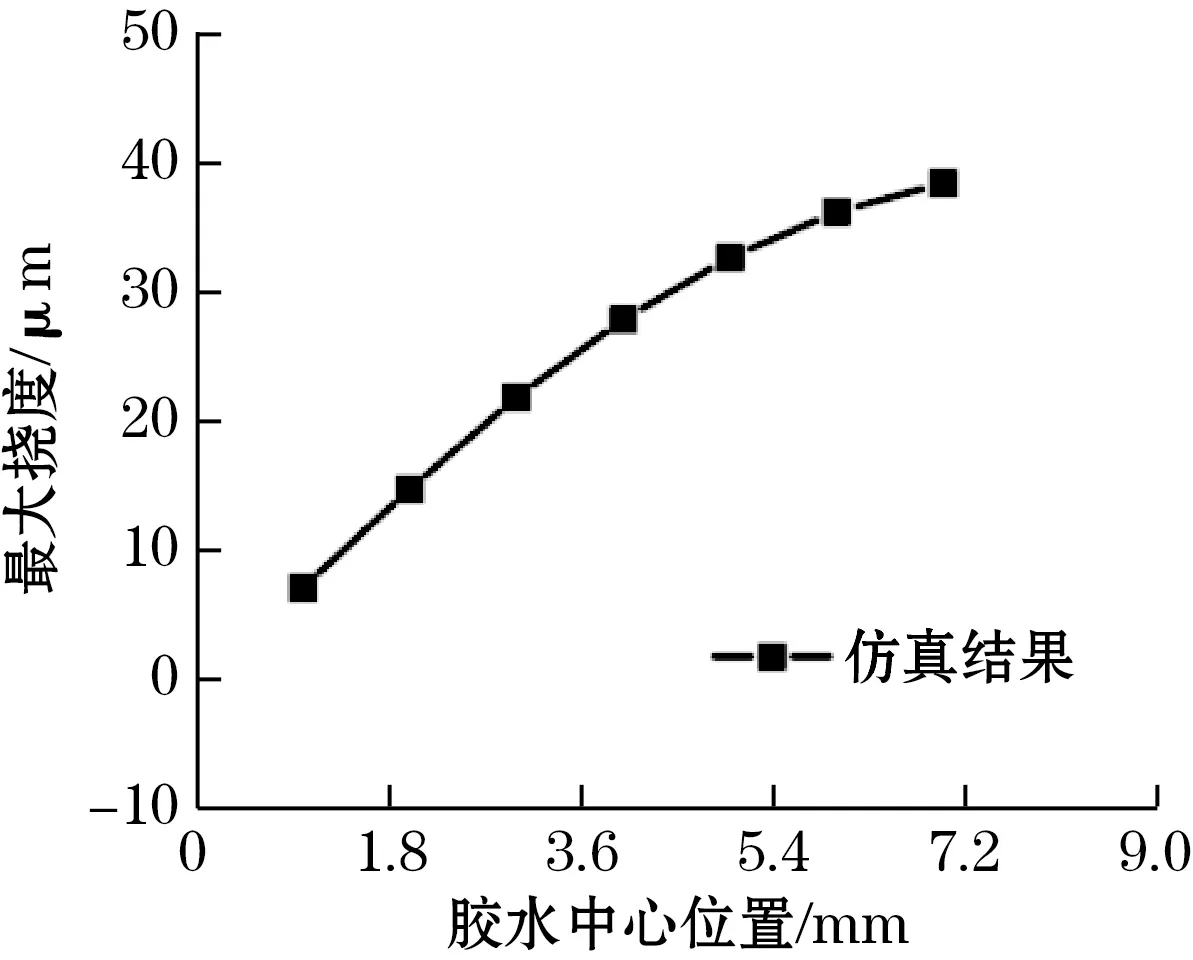
(c)芯片最大挠曲变形与点胶中心位置关系

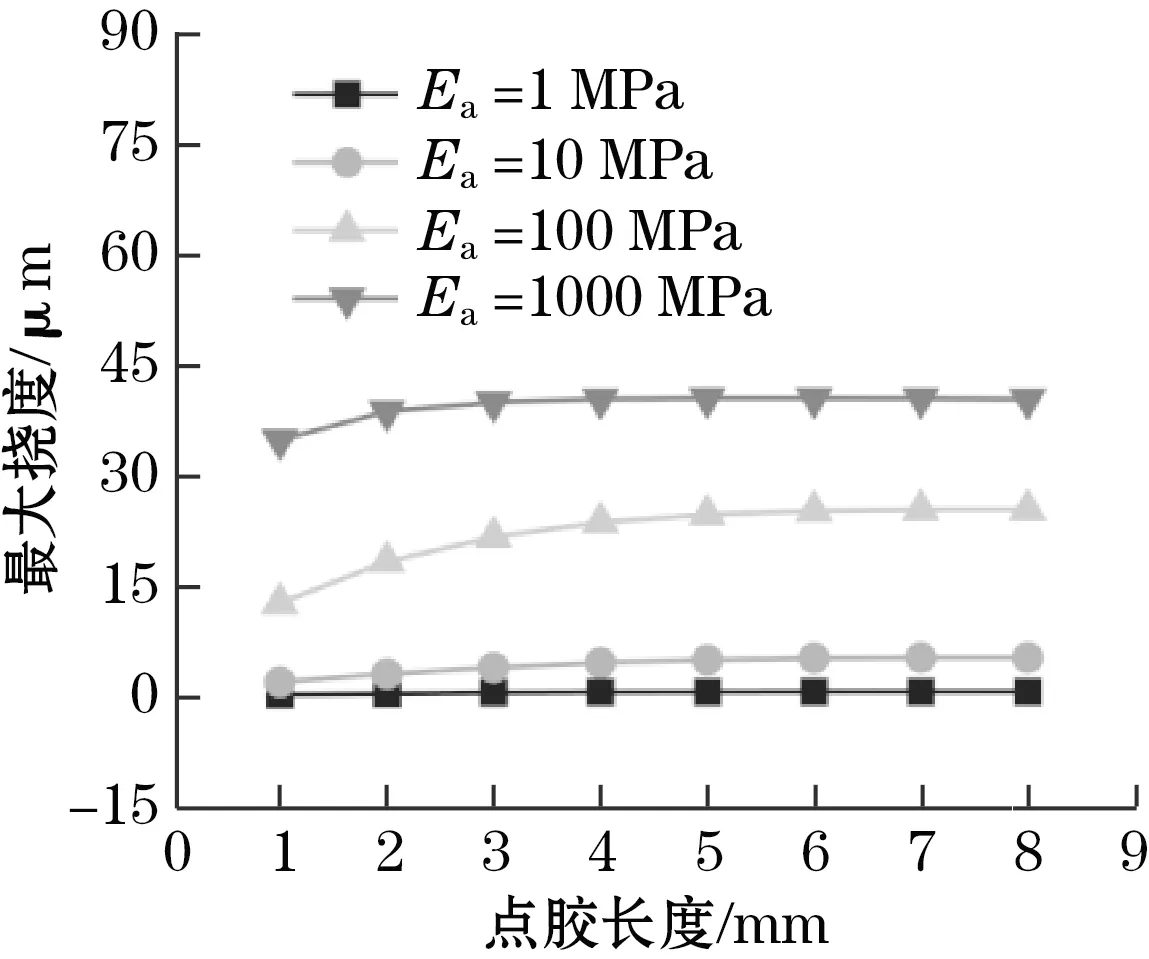
(d)芯片最大挠曲变形与点胶长度关系

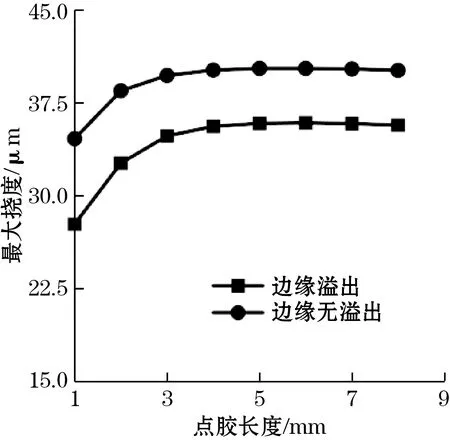
(e)芯片最大挠曲变形与胶水溢出关系图5 芯片最大挠曲变形与贴片工艺参数关系

图5(a)表明,芯片基底间热膨胀系数差与层合结构最大挠度呈线性关系。当芯片与基底间热膨胀系数差从0增至20 ppm/K时,最大挠度从0增大为144 μm。图5(b) 中,热固化温度差与层合结构最大挠度呈线性关系,温度变化为100 K时,铝合金基底最大挠度分别为160 μm,而氧化铝陶瓷、硅片和石英玻璃基底则分别为39、0、-16 μm,这种挠度差异主要是基底芯片间热膨胀系数差造成的。

图5(c)中,最大挠度随点胶位置靠近层合结构边缘而增加。实际微镜贴片采用四点粘合,点胶位置约在距离微镜长边中心6～7 mm处,对挠度仅产生2 μm左右的影响。图5(d) 中,胶水的粘接长度对热变形影响基本可以忽略不计。图5(e)中,胶水溢出使基底粘接位置附近应力降低,最大挠度相比无溢出时下降约10%。

通过本节分析可知,温度、芯片与基底间热膨胀系数差是影响贴片热变形的2个主要因素。因此,选择热固化温度较低的胶水或选择热膨胀系数与芯片相近的基底材料均可有效降低残余变形。

2 残余应力表征

结合层合梁热变形理论[19]分析可知,微镜贴片残余应力以轴向正应力为主;剪切应力和剥离应力集中在层合结构边缘,最大值约为3 MPa,相较正应力可以忽略不计,因此,本节将残余应力等效为轴向应力,围绕轴向应力与微镜模态频率偏移特性间的关系展开研究,并得出一种针对电磁MEMS微镜的简单贴片残余应力表征方法。

本文研究的电磁MEMS微镜Piston模态为二阶模态,振型为镜面、镜框和镜轴沿垂直微镜平面方向平动。轴向拉伸或压缩应力影响镜轴平动刚度,从而引起Piston模态频率偏移。

下面采用集中质量法建立微镜动力学模型,如图6所示。镜面抗弯刚度均远大于镜轴,故忽略镜面变形,将其视为刚体,简化为双端固支梁中心处质量块m。由于镜轴相对镜面质量可以忽略不计,m即为镜面质量。竖直载荷P作用在中心位置处,其产生的纵向位移为u。

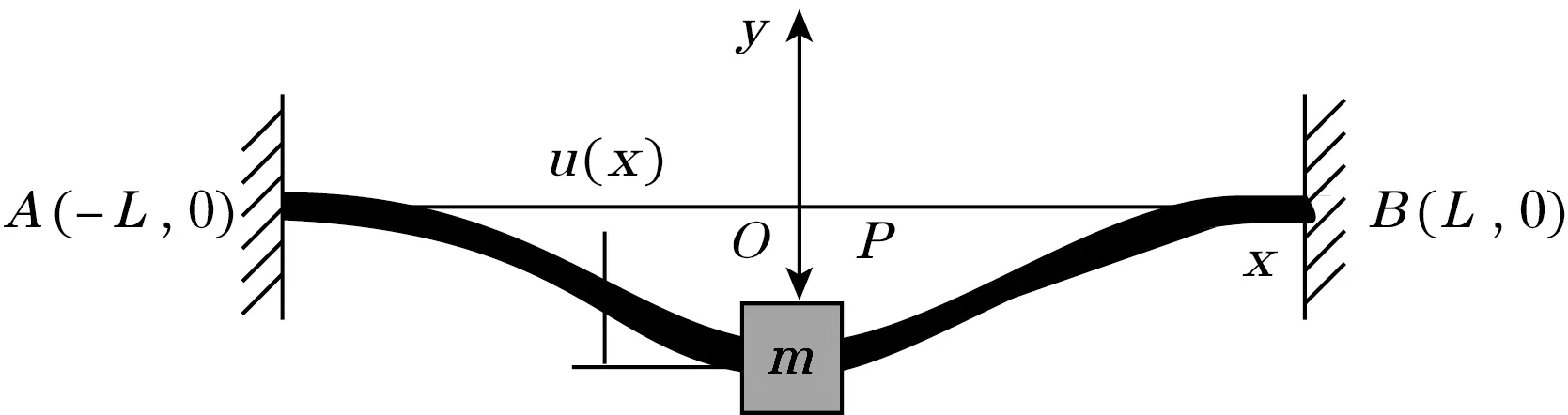
图6 Piston模态等效模型

假设微镜仅在线性范围内以微小幅度振动,则微镜Piston模态的动力学方程为

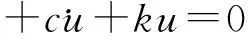
(7)

式中:m为微镜质量,m=6.730 8×10-6kg;k为微镜的平动刚度,N/m;u为y方向位移,m;ü为位移对时间的二阶导数;c为系统的阻尼系数。

考虑到热变形导致的残余应力主要为沿x方向的中面应力N,小变形下镜轴内部应力可视为均匀应力。使用含有中面应力的欧拉方程来表示梁的弯曲,有:

(8)

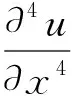
定义参数:

(9)

则镜面的挠度方程为

u=C1cosh(λx)+C2sinh(λx)+C3x+C4

(10)

式中C1～C4为方程的待定常数。

双端固支梁中点竖直载荷的边界条件为

(11)

式中:l为镜轴长度,l=2.2 mm;P为竖直方向集中载荷,P=1 N;D为镜轴抗弯刚度,D=2.073 1×10-7N·m2。

代入求得中面应力下梁的挠度曲线u,则可得到载荷P作用下梁中点处的位移u(0) ,进一步地,可求得支撑梁的平动刚度k为

(12)

则微镜系统的Piston模态无阻尼谐振频率f为

(13)

表3给出微镜Piston模态动力学模型使用的相关参数。

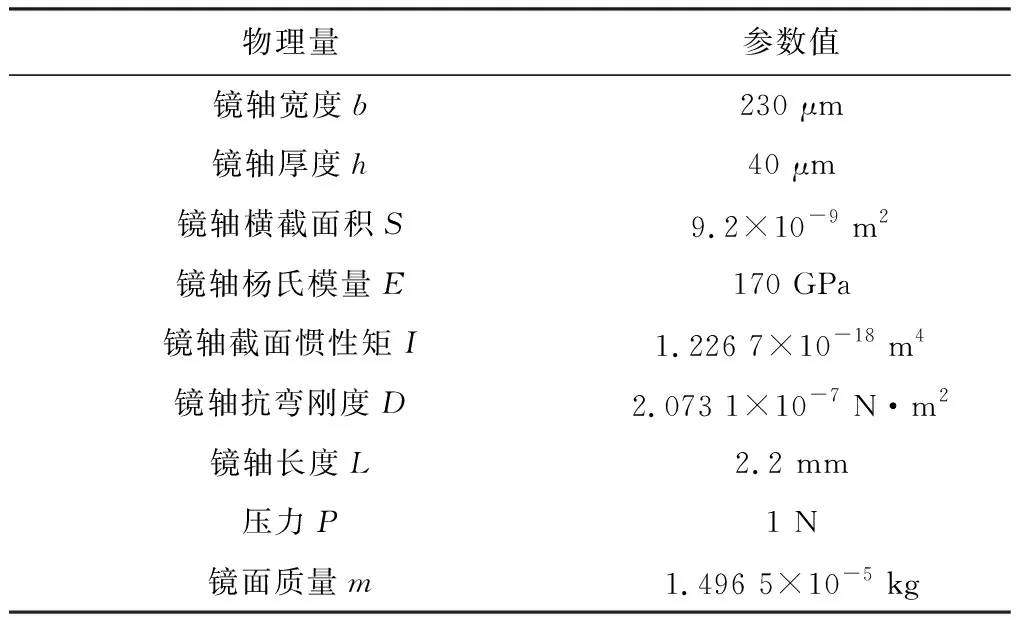
表3 微镜Piston模态模型参数表

微镜轴向应力与频率偏移关系的理论和仿真结果如图7所示。图7(a) 中,当微镜支撑梁的轴向应力为拉伸应力时,Piston模态特征频率向高频漂移,并且频率偏移程度随拉伸应力增大而增加;当微镜支撑梁轴向应力为压缩应力时,微镜Piston模态谐振频率向低频漂移,并且频率偏移程度随着压缩应力增大而增加。通过理论计算与仿真分析,得到微镜无残余应力状态下的谐振频率分别为889.12 Hz和891.49 Hz,误差为0.2%。

(a)轴向应力与Piston模态谐振频率关系图

(b)轴向应力与Piston模态频率改变量关系图图7 MEMS微镜频率漂移特性

定义频率改变量为特征频率相对于无应力下谐振频率的改变程度,轴向应力与频率改变量的关系如图7(b) 所示,应力水平越高,频率偏移程度越大,仿真结果与理论模型误差小于7.1%,误差的来源为:理论模型采用双端固支梁模型的边界条件进行求解,而实际情况下支撑梁根部的转角情况较为复杂。整体理论与仿真结果一致,此方法具有可行性。

3 微镜贴片封装和频率测试

基于前述理论和仿真分析结果,选取温度变化、热膨胀系数差、基底厚度、Y方向点胶位置作为实验变量。微镜贴片样品制备流程如图8所示,在25 ℃室温下,于基底四角标定位置处均匀点胶,将微镜沿标定位置进行贴片,待胶水流平后,最终形成直径2 mm、厚度100 μm的胶层,样品放入真空干燥箱中,设置固化温度并加热30 min,固化完成后缓慢降至室温。实验选用的基底材料见表4。

图8 贴片微镜样品制备流程

表4 微镜贴片封装样品基底参数表

贴片芯片的频率偏移测试流程如图9所示,对贴片后的样品进行Piston模态频率偏移实验测试,每个贴片微镜样品测得的频率偏移量通过第2节所建的残余应力-频率偏移模型计算对应的残余力,结果如图10所示,并与前文中的理论和有限元结果进行对比。

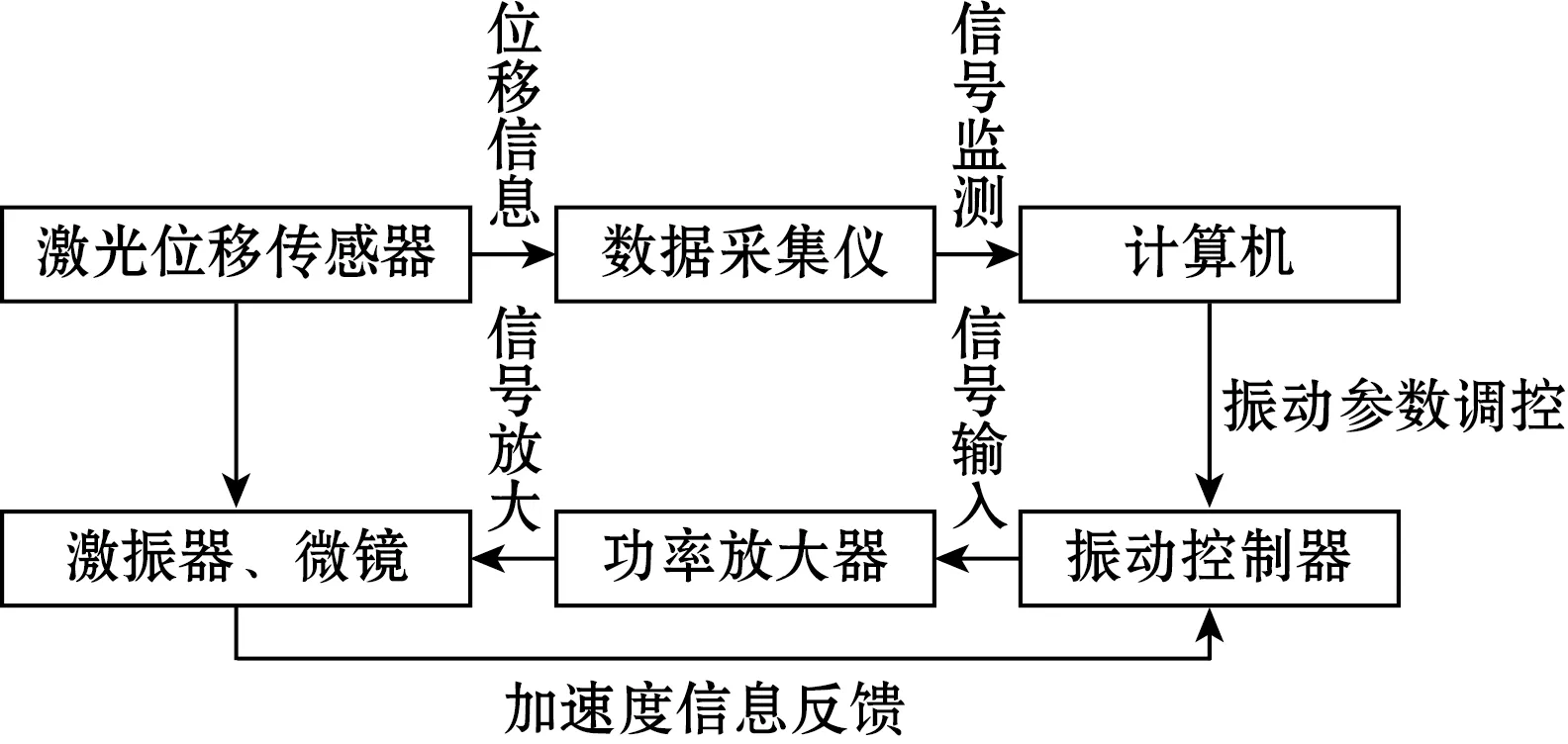
图9 实验流程

图10(a)显示了残余应力与温度变化的关系,分别采用75 ℃和175 ℃固化温度的胶水粘接,对应50 ℃和100 ℃的温度变化,结果显示,微镜内部的残余应力在高温胶水贴片下显著增大,而低温下不同基底的样品贴片残余应力均处于相对较低水平。

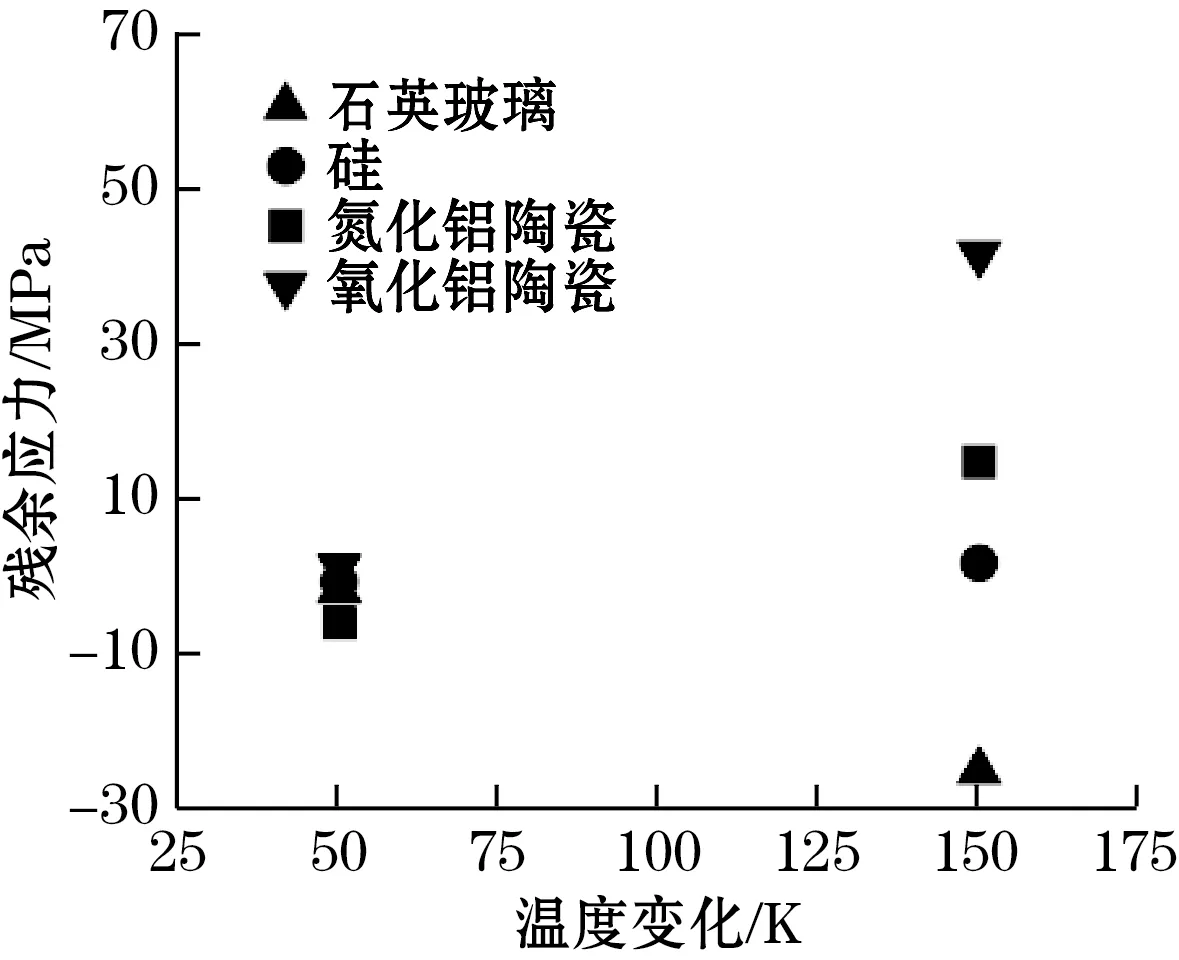
(a)残余应力与温度变化关系

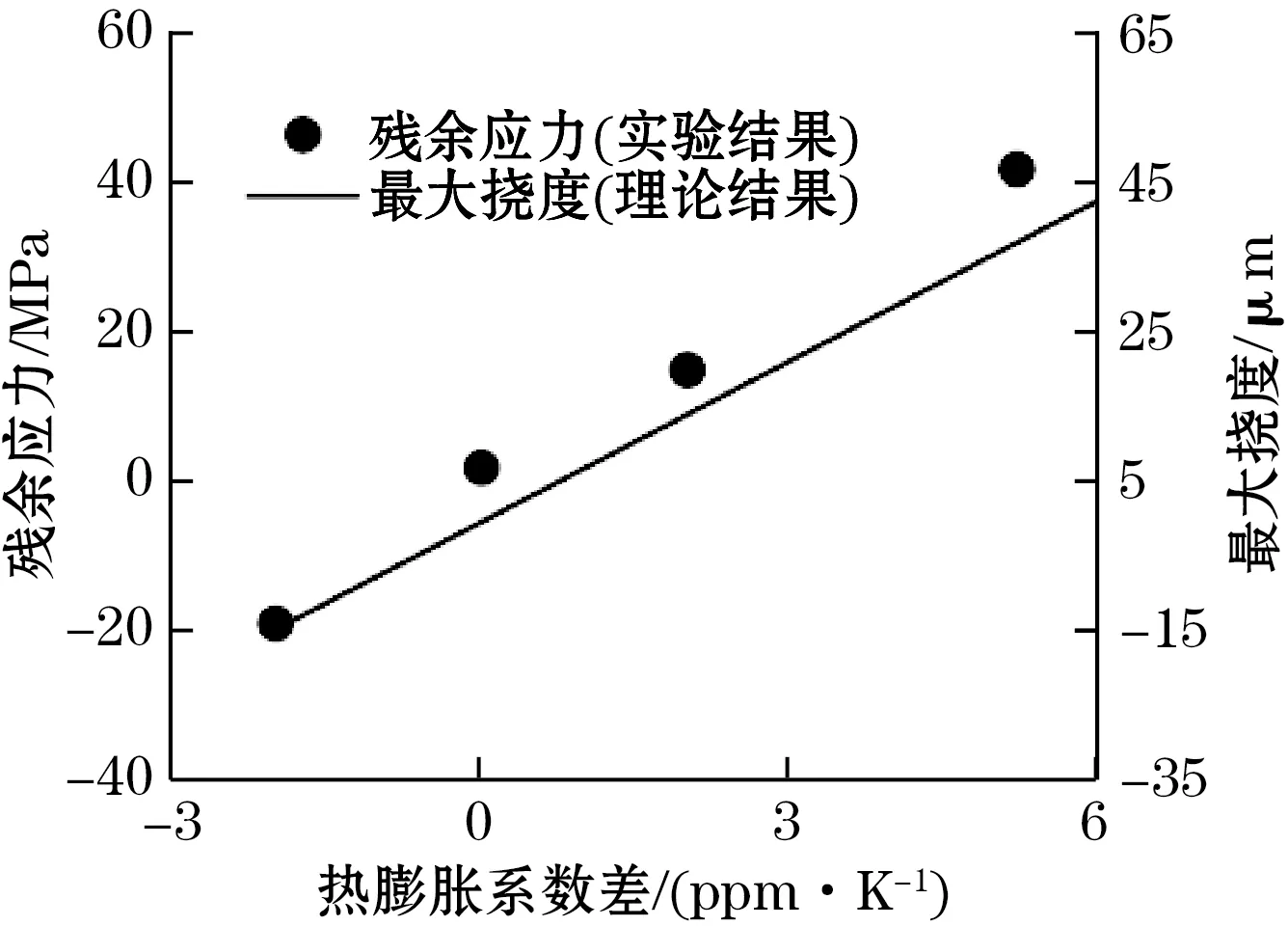
(b)残余应力与热膨胀系数差关系

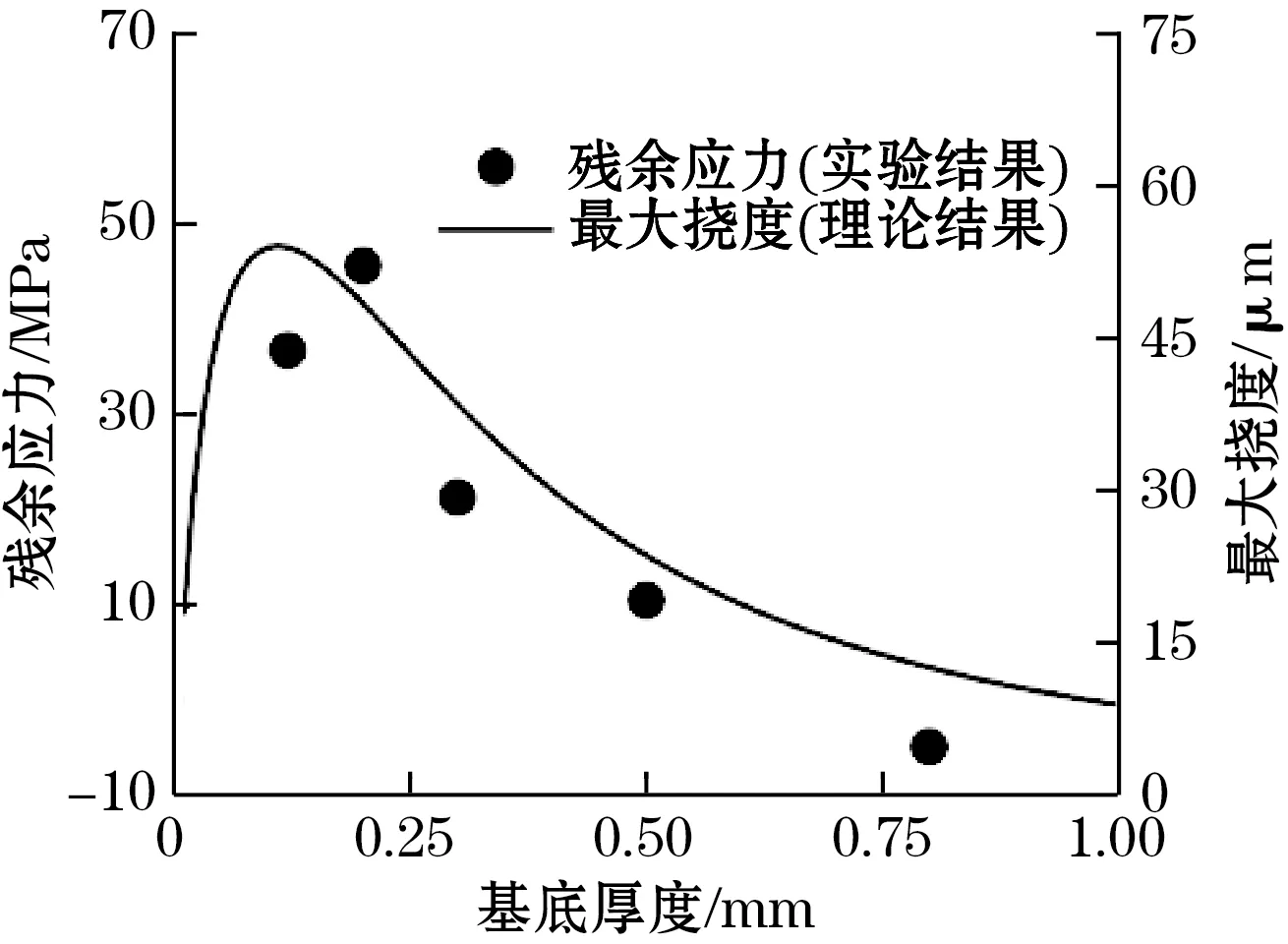
(c)残余应力与基底厚度关系

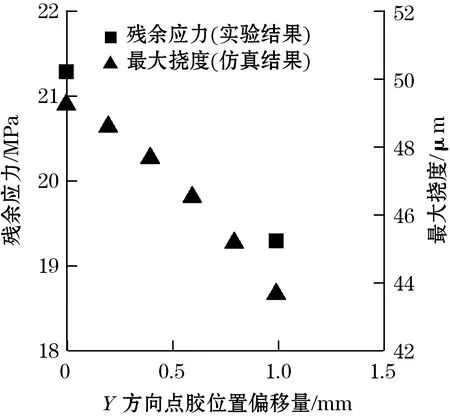
(d)残余应力与Y方向点胶位置偏移量关系图10 轴向残余应力随封装参数变化规律

理论和实验结果对照如图10所示,验证了理论模型的正确性。其中,图10(b)显示了芯片与基底的热膨胀系数差对残余应力的影响,数据点呈近似线性分布,与仿真结果较为一致,误差来源是不同材料之间弹性模量的差异。图10(c)中,随着基底厚度增加,芯片中残余应力水平先升高后降低,实验数据和最大挠度理论曲线在转折处所对应的基底厚度略有差异,误差来源于热变形与热应力间的差异性。

实验所用的基底的模量高于芯片,当基底厚度较薄时,基底的抗弯刚度低于芯片,而基底变形不足以驱动芯片挠曲变形,过薄的基底甚至会因为变形超出弹性范围而出现脆性断裂,所以芯片的挠度较小。随着厚度增加,基底抗弯刚度上升,对芯片的驱动力增强,芯片挠曲变形加剧;当厚度继续增加,基底的抗弯刚度随之增大,芯片热变形对基底产生的影响减弱,进而抑制了芯片的挠曲变形。

点胶位置与残余应力的关系如图10(d)所示,规定标定位置为点胶原点,靠近中心为正,远离中心为负。点胶位置沿Y轴向中心偏移,芯片中的残余应力下降,与仿真显示的挠度结果趋势一致,受基底尺寸与胶水流动性限制,点胶可以选取的位置较为有限,因此实验数据点较少。

4 结束语

本文通过层合梁热变形理论,研究了贴片材料物理参数与贴片工艺参数对MEMS微镜贴片残余应力的影响规律。结果表明,温度和芯片基底间热膨胀系数差是影响贴片残余应力的重要因素,与贴片残余应力均呈线性关系;基底厚度和模量影响了基底抗弯刚度,从而影响了芯片的翘曲程度。

利用共振频率测试的方法表征电磁MEMS微镜的贴片残余应力。通过测量贴片微镜Piston模态的频率偏移程度间接推算出轴向残余应力,相比拉曼光谱法和表面轮廓测量法,对设备要求较低,可行性更强;与接触式测量方法相比,具有不损伤器件的优势,为微镜贴片封装残余应力的评估提供了参考。

理论、仿真与实验结果均表明,微镜贴片封装时,选用固化温度较低的胶水、与芯片热膨胀系数相近的基底材料以及厚度较大的基底均可以有效地控制残余应力。