便携式平行板结构介电常数测量仪的设计

赵戊寅,陈新伟,马润波

(山西大学物理电子工程学院,山西太原 030006)

0 引言

介电常数作为材料的特性参数之一,在很多科研和工程应用中需要确定。常见介电常数测量方法有谐振腔法[1]、自由空间法[2]、传输线法[3]和电容法[4]等。其中电容法具有成本低、线性度好、操作简便等特点,应用于很多实用仪表。然而,电容传感器精度主要受限于寄生电容的影响,因此需采取相应措施对传感器结构做出改进。常用方法如文献[4]在平行板电容传感器的一个极板上添加等位环,用以减小边缘效应对传感器精度的影响。文献[5-6]中,将平行板电极封闭在接地屏蔽罩中,减小寄生等干扰因素影响。

受尺寸参数的影响,电容传感器通常是微小电容,易受干扰影响,方便准确地测得传感器电容具有重要意义。电容传感器的测容方法常见有调频式[7]、交流激励式[8]、开关充放电式以及专用芯片等。文献[9]中,将电容传感器作为方波发生电路的一环,通过检测电路输出频率实现传感电容的测量。该测容方法具有分辨率较高和测容范围宽等优点。对于平行板结构的电容传感器,文献[10-11]采用了非稳态多谐振荡器设计电容检测电路,通过测得振荡周期或频率间接求解待测介质的介电常数值,并引入了校正因子减小边缘效应的影响。文献[12-13]则将传感器与电阻、电感组成RLC谐振电路,由电路的谐振频率和电感量求解传感器电容值,进而求得介电常数值。

本文设计的介电常数测量仪,由平行板电容传感器和辅助电路系统对待测介质进行测量。采用PCB工艺实现传感器的多层平面结构设计,便于引入保护环来降低小尺寸传感器的边缘效应,提高传感器精度。经检测电路实现电容频率转换,屏蔽的信号连接减小了系统中寄生电容和外部干扰的影响,由单片机模块测量信号频率并计算得出待测介质的相对介电常数。设计的测量仪具有结构简单、成本低和便携的特点。

1 传感器原理与仿真

图1为基本平行板电容传感器示意图,将待测介质放置到平行板电容传感器极板之间,可以通过测得传感器电容值求解对应介质的介电常数值。图1(a)所示传感器由极板1和极板2组成,当极板尺寸远大于极板间距时,电能绝大部分存储在极板间而忽略电场边缘效应,极板间电容Cx可由理想公式计算:

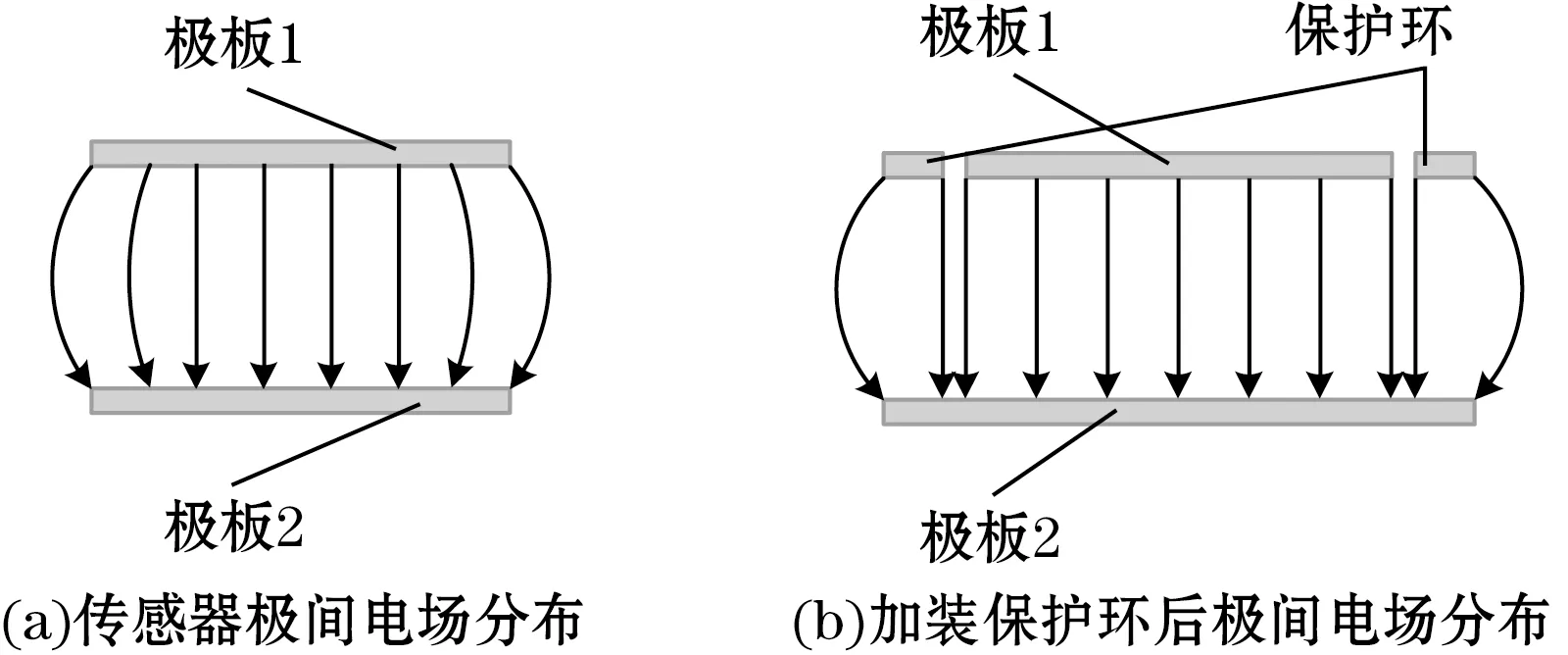
图1 平行板电容传感器示意图

(1)

式中:ε0为真空介电常数;εr为待测介质的相对介电常数;S和d分别为极板面积和间距。

平行板电容传感器尺寸变小时,边缘效应产生的电容相对变大,其值随极板间距增大而增大,使得式(1)不再准确。为消除边缘效应,加装等电位保护环是常用有效方法。如图1(b)所示,当保护环与极板1等电位时,边缘电场转移到保护环边缘,取极板1的有效面积带入理想公式计算极板间电容的误差较小。因此需要合理设计电容传感器结构,在小误差情况下使用理想公式。

图2给出传感器模型的原理结构,主体由极板1、极板2和极板1的保护环组成,待测介质紧密贴合于两极板之间。为便携设计,将极板1设定为边长25 mm的矩形贴片,同层保护环与极板1间距为s。为使传感器实物便于用双面PCB加工制作,极板1与保护环制作在同一块FR-4基板上,并通过板周围加装金属墙将保护环的顶层和底层金属连接在一起。考虑到传感器和电路系统的整机组装,依照单片机模块尺寸将极板所在基板尺寸设计为50 mm×50 mm×1.6 mm,模型尺寸参数由表1给出。

表1 电容传感器模型尺寸参数 mm

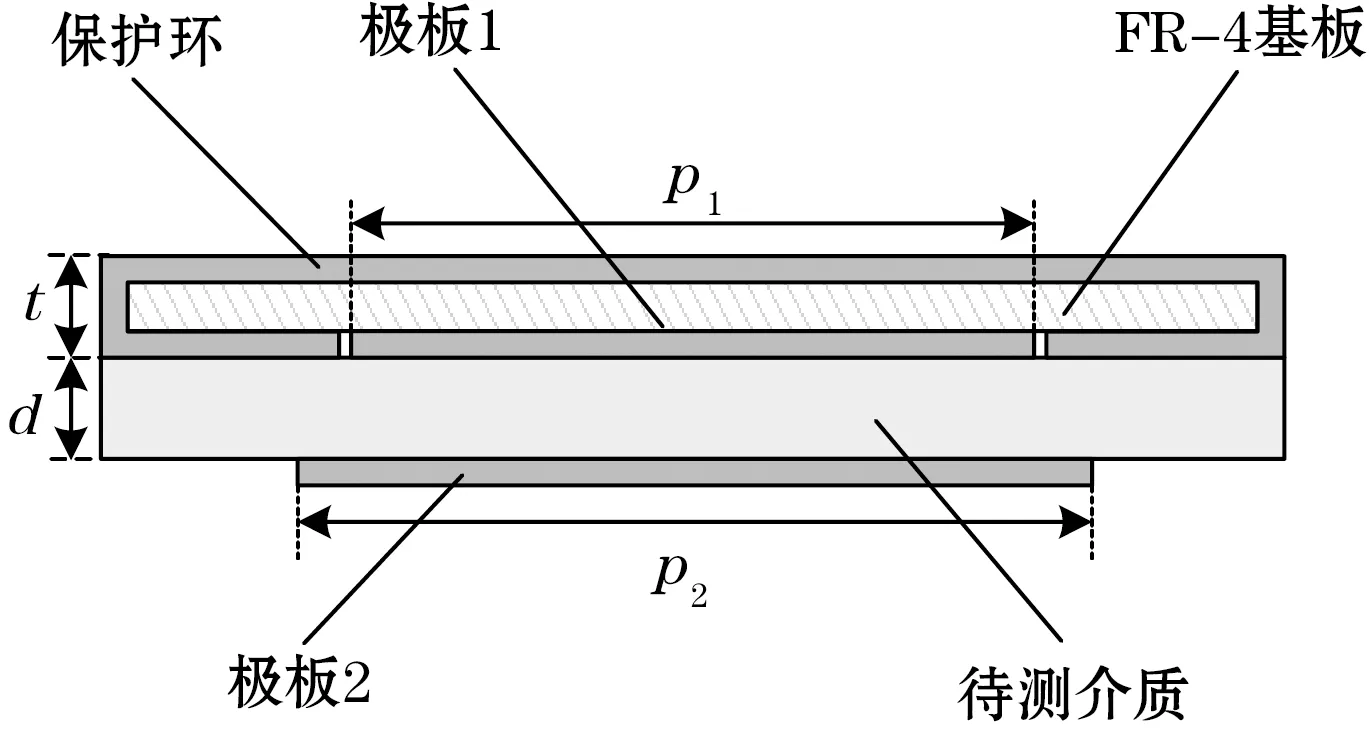
(a)电容传感器截面

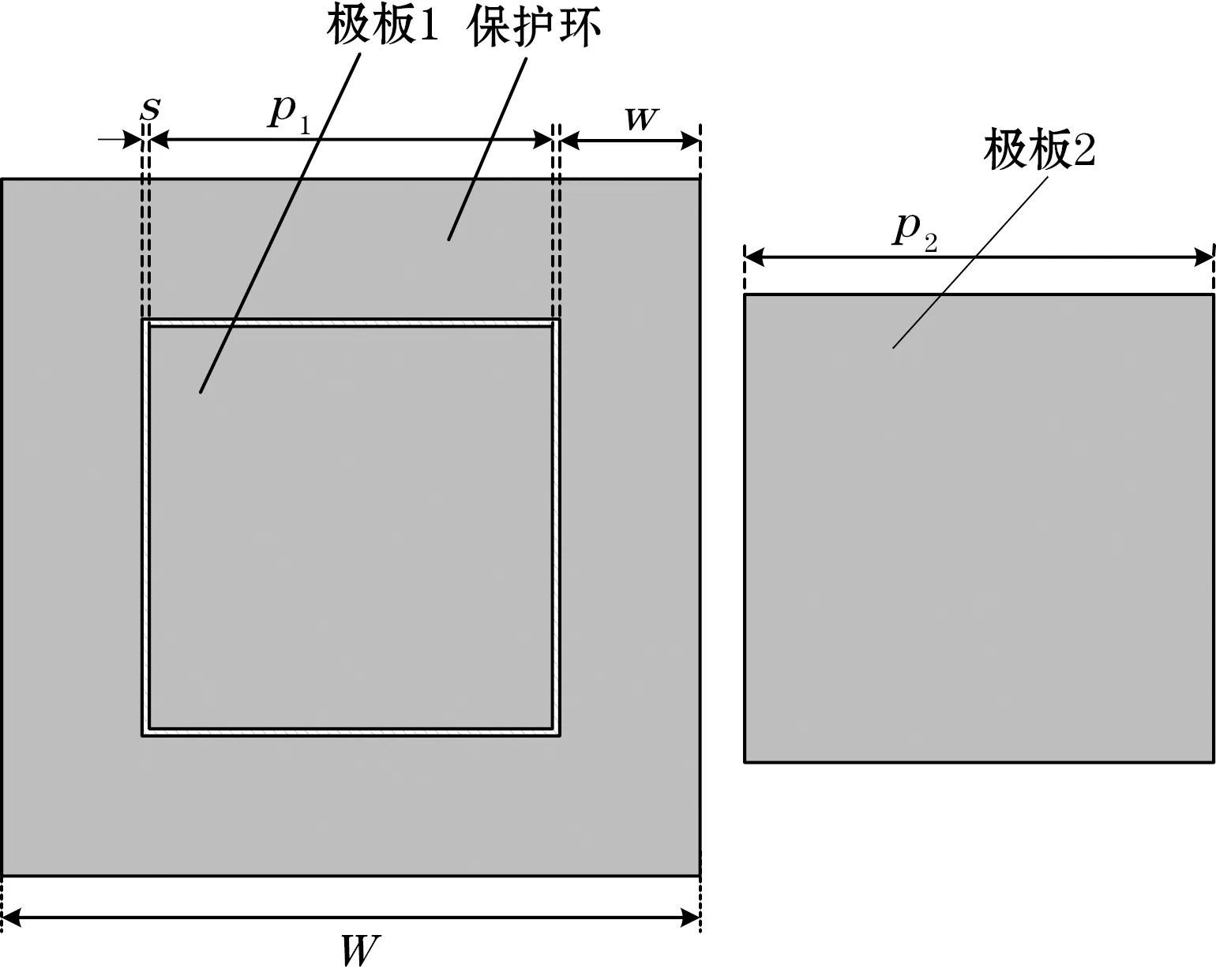
(b)极板1、2正视面图2 平行板电容传感器仿真模型

利用CST微波仿真软件的静场分析模块对传感器模型进行了建模和仿真。在待测材料相对介电常数为1时,通过仿真分析确定保护环的几何参数。在极板1和保护环不同间距s下,图3给出极板间电容仿真值和式(1)理想值之间的误差。可见减小s可减小误差,结合精度要求和PCB制作工艺,s取0.508 mm。此外,保护环宽度w对传感器精度也有影响,图4给出仿真值和式(1)理想值之间的误差随保护环宽度的变化关系,可见当w大于3 mm以后,保护环效果提升不明显。鉴于极板所在基板最大尺寸W已定为50 mm,则保护环宽度w可设计为11.992 mm,满足稳定测量的要求。

图3 仿真值和公式理想值之间的误差与极板1和保护环间距s的关系

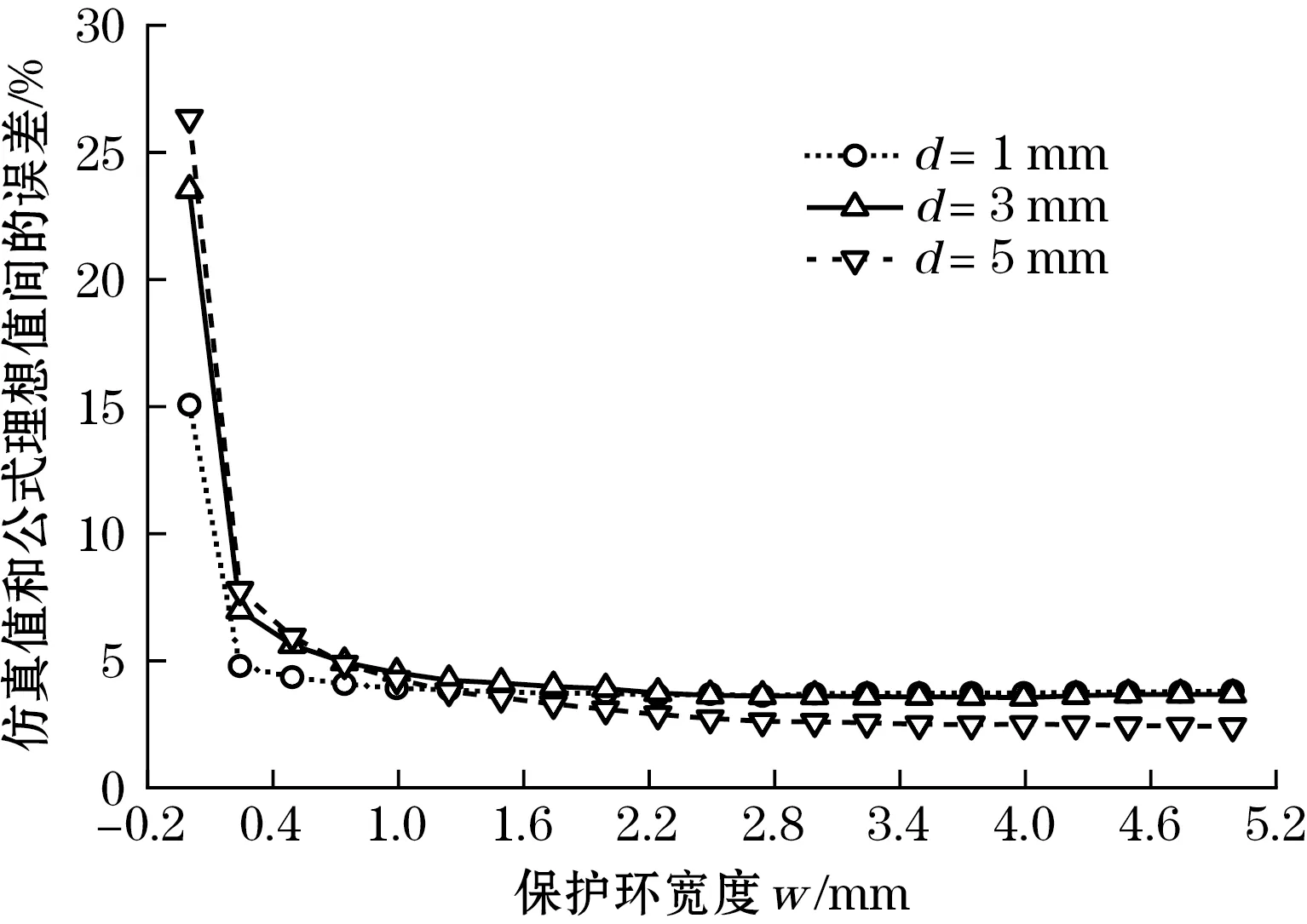
图4 仿真值和公式理想值之间的误差与保护环宽度w的关系

2 电容检测电路与测量系统分析

2.1 电容检测电路原理

图5为电容频率转换电路,运放1为迟滞电压比较器,运放2为积分器,传感器电容作为积分电容Cx通过同轴线接入电路。分析可知电路输出信号Vo1的频率f与待测传感电容Cx间的理论关系为[14]

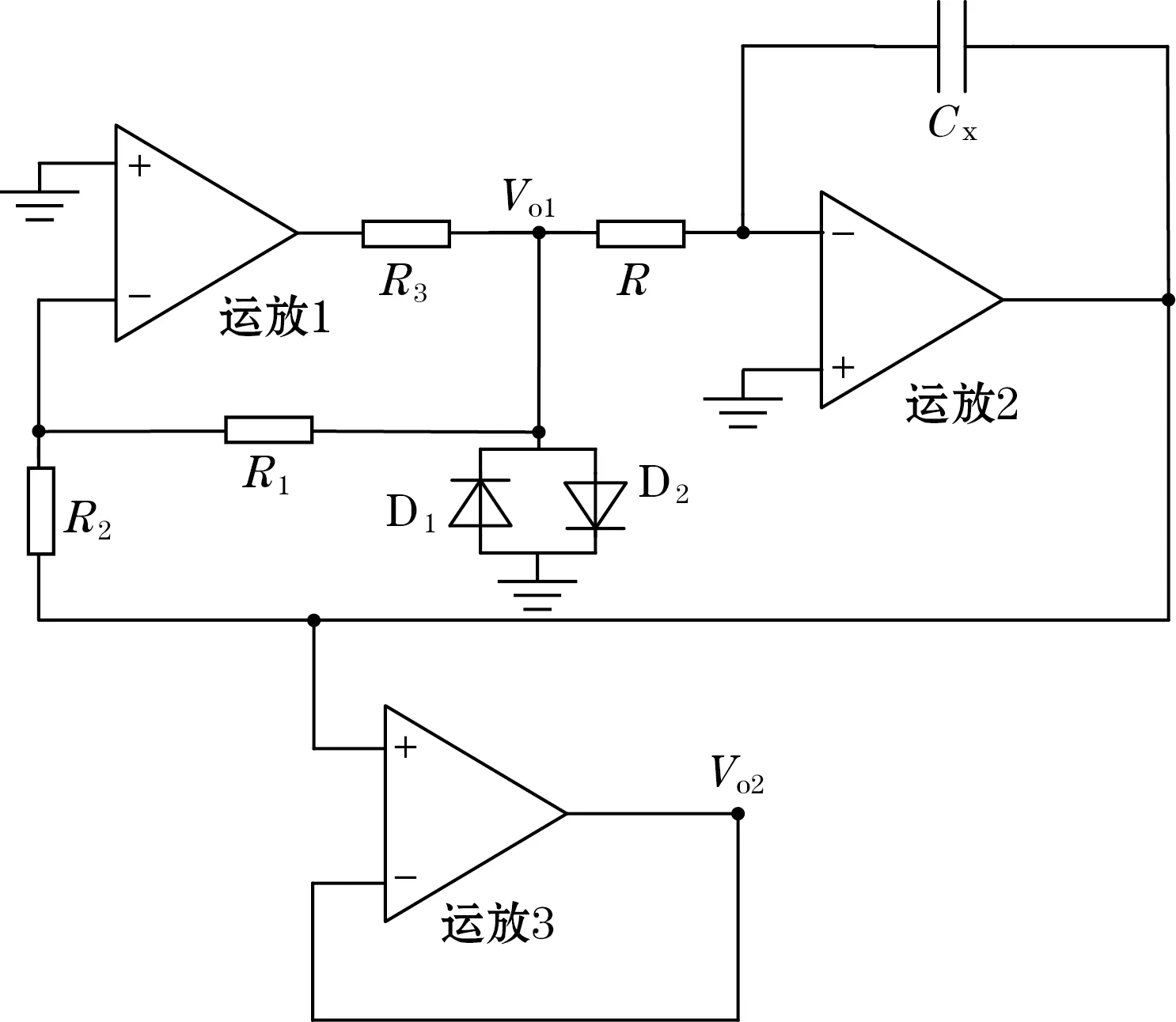
图5 电容频率转换电路

(2)

式中:R、R1、R2为电容频率转换电路中的关键电阻,R=510 kΩ,R1=R2=100 kΩ。

在图5中,R3=10 kΩ,二极管D1、D2型号为1N4148,运放1、2、3型号为TL074ACD。此外,运放3作为电压跟随器,其输出信号Vo2驱动极板1的保护环,实现等电位保护。为屏蔽外界干扰,实际设计中,将极板2也设置保护环并接地。对于大部分常见介质,由式(1)计算可知设计的电容传感器输出电容范围为1 pF至100 pF,该范围电容对应的输出信号频率范围在100 kHz以下,便于单片机频率测量。

2.2 测量系统分析

测量系统中存在不确定的寄生电路参数,如极板上绝缘层产生的串联电容Ca、电路元件间寄生电容Cs以及测量电路的响应时间td。基于式(2),分析可得电路输出频率f与传感器电容Cx及各寄生参数之间的关系如下:

(3)

式中a为待确定的比例系数。

一般情况下两极板上绝缘层的厚度远小于待测介质的厚度,使Ca远大于Cx,Ca和Cx串联后等效电容值趋于Cx,因此式(3)中可忽略Ca。结合式(1),简化频率f与待测相对介电常数εr的关系为

(4)

式中b为与电路特性相关的待定系数,b=aCs+td,系数a和b在实际校准过程中确定。

改写式(4),得到通过频率f计算待测相对介电常数εr的表达式:

(5)

3 实测与误差分析

采用PCB工艺制作传感器和转换电路的多层平面结构,图6给出组装的介电常数测量仪原型实物。关键模拟信号的同轴连接减小了系统中寄生电容和外部干扰的影响,经单片机测量电路输出信号的频率并计算得到待测介质的相对介电常数。

图6 介电常数测量仪实物

实测前,需经过校准确定式(4)中未知系数。空气相对介电常数可看作1,工程中常用作易得的标准材料[15]。测量并记录空气中不同极板间距d和对应频率f,拟合确定未知系数a和b。为减小拟合误差,进行了3组测量,每组测量8个不同间距的数据。通过曲线拟合得到a=3.984×106,b=1.637×10-5,拟合优度R2=0.997,依据测得数据,得到频率倒数与极板间距的关系曲线如图7所示。

图7 频率倒数f-1与极板间距d的关系曲线

将a、b、ε0和S的值代入式(5),令频率f单位为kHz,厚度d单位为mm,得到本测量仪原型的相对介电常数计算公式:

(6)

实物测量中使用了PTFE基板、树脂玻璃G和FR-4基板作为样品,用以检验测量仪原型测量介电常数的性能。将各介质基板加工成40 mm×60 mm的平板,使用千分尺测得各自厚度。表2给出样品相对介电常数的实测结果。

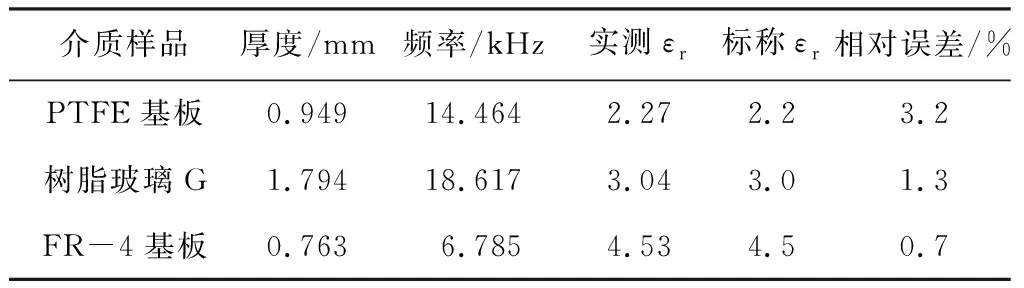
表2 样品相对介电常数的实测结果

表3为文献[11-13]中所用传感器和样品相对介电常数的测量结果。文献[11]所使用的传感器尺寸较小,电容检测电路简单,测量系统成本较低,测量误差较大。文献[12-13]测量精度较高,但采用了大尺寸传感器,测量电路基于RLC谐振电路,设计成本较高。与文献[11-13]相比,本文提出的设计具有小尺寸和低成本特点,能够以较低误差方便地测量待测样品。

表3 参考传感器的测量结果

4 结束语

本文采用电容法,设计了一种便携式介电常数测量仪。通过采用PCB工艺搭建了介电常数测量仪实物,并校准得到了用于计算相对介电常数的拟合公式。实测结果表明该测量仪在满足小尺寸、低成本的前提下,测量相对误差在3.2%以内,可满足大部分实际工程所需。