基于数学运算素养的高三复习实践与思考

刘凤珠

摘要：数学运算是六大核心素養中最基本的素养，是学生学习数学的必备能力.从2022年新高考全国卷可以看出，整张试卷计算量非常大，很多考生时间都不够用.如何培养学生的运算能力，使其在有限的两小时内尽可能快速准确地解决问题，是每位教师面临的一大难题.若仅靠大量的机械运算，往往收效甚微，这就需要教师合理设计好每一堂课，落实到每一道具体题目中.本文以三角恒等变换为例，谈一谈如何培养学生的数学运算能力.

关键词：数学运算；三角恒等变换；课堂教学

1问题提出

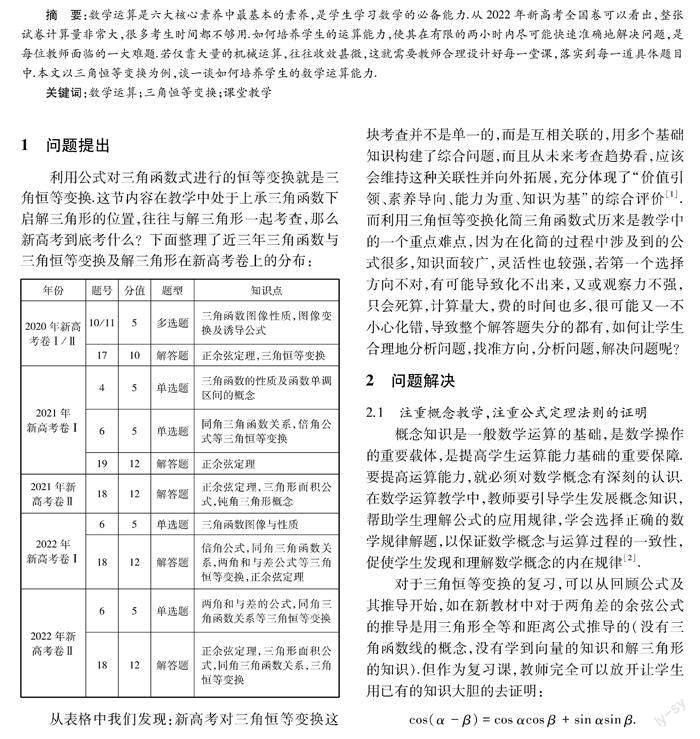
利用公式对三角函数式进行的恒等变换就是三角恒等变换.这节内容在教学中处于上承三角函数下启解三角形的位置，往往与解三角形一起考查，那么新高考到底考什么？下面整理了近三年三角函数与三角恒等变换及解三角形在新高考卷上的分布：

从表格中我们发现：新高考对三角恒等变换这块考查并不是单一的，而是互相关联的，用多个基础知识构建了综合问题，而且从未来考查趋势看，应该会维持这种关联性并向外拓展，充分体现了“价值引领、素养导向、能力为重、知识为基”的综合评价［1］.而利用三角恒等变换化简三角函数式历来是教学中的一个重点难点，因为在化简的过程中涉及到的公式很多，知识面较广，灵活性也较强，若第一个选择方向不对，有可能导致化不出来，又或观察力不强，只会死算，计算量大，费的时间也多，很可能又一不小心化错，导致整个解答题失分的都有，如何让学生合理地分析问题，找准方向，分析问题，解决问题呢？

2问题解决

2.1注重概念教学，注重公式定理法则的证明

概念知识是一般数学运算的基础，是数学操作的重要载体，是提高学生运算能力基础的重要保障.要提高运算能力，就必须对数学概念有深刻的认识.在数学运算教学中，教师要引导学生发展概念知识，帮助学生理解公式的应用规律，学会选择正确的数学规律解题，以保证数学概念与运算过程的一致性，促使学生发现和理解数学概念的内在规律［2］.

对于三角恒等变换的复习，可以从回顾公式及其推导开始，如在新教材中对于两角差的余弦公式的推导是用三角形全等和距离公式推导的（没有三角函数线的概念，没有学到向量的知识和解三角形的知识）.但作为复习课，教师完全可以放开让学生用已有的知识大胆的去证明：

教师可以有选择性的去引导学生选择证明的方法，如可以选择以下两个方法.

方法1：构建单位圆转化为向量，用向量的数量积证明.

方法2：构建单位圆转化到三角形中，用余弦定理及两点间距离公式证明或三角形全等及两点间距离公式证明.

课标中明确指出数学运算是指在明晰运算对象的基础上，依据运算法则解决数学问题的过程，主要包括：理解运算对象，掌握运算法则，探究运算方向，选择运算方法，设计运算程序，求得运算结果等［3］.这样的设计使学生充分了解公式的来龙去脉，既证明了公式加深了印象，让学生更好地转化为自己的知识，更灵活地去运用它，又复习了向量的数量积，解三角形等知识，让学生体会到知识是环环相扣的，感受数学运算的魅力，更好地提高对运算的兴趣.因此教师要对定理、公式等的证明进行讲解，帮助学生更加深入地了解其中的内在关系、理解其中的运算对象，从而提高学生的数学运算素养.

2.2注重例题分析

这里以教学中的几个片段为例

教学片段1

化简：（2cos4x－2cos2x＋（1 2  2tan（（π 4 －xsin2（（π 4 ＋x ＝______.

本题看着有点复杂，所以部分有畏难心理的学生已经放弃尝试了，另外部分学生无方向的尝试后并没有化简出来，也说明了这些同学可能公式并不是很熟练，以下为几位化简出来的同学的解题思路.

生1：分子上先提出个2，里面是个完全平方，再用降幂公式2JB（（cos2x－ 1 2 2=2 1+cos2x 2 － 1 2 2= 1 2 cos22x，分母上先切化弦，然后全部展开 2  2  2 cosx－  2  2 sinx）   2  2 cosx+  2  2 sinx ·  2  2 cosx+  2  2 sinx）2=2  2  2 cosx－  2  2 sinx）·  2  2 cosx+  2  2 sinx）

=cos2x－sin2x=cos2x，

最终结果是 1 2 cos2x.

生2：我分母上没看出来是完全平方，直接用降幂公式代入化简，再展开计算就可以了2 1+cos2x 2 2－2· 1+cos2x 2 + 1 2 = 1 2 cos22x，分母上和生1是一样.

生3：我是看到前面次数较高，就提了个cos2x出来试试，化着化着就出来了，

分母也是和前面两位同学一样做的.

师：很好！生1的观察能力强，发现了分子上是个完全平方，再用降幂公式处理，很快解决了，但若能结合二倍角公式提个 1 2 ，里面直接是cos22x就更快了；生2看见次数高，能想到降幂公式降次处理，是我们常用的方法，也能大胆的全部展开尝试下去，很不错；生3虽然看着无方向但有公因式提取公因式后，能用同角三角函数关系式逆用，倍角公式的逆用进行化简，就要做到底，不半途而废，也很不错.从解答中可以看出三位同学都熟练掌握了公式，但分母的处理都是直接展开计算的，我们一起观察一下，里面出现了 π 4 －x， π 4 +x这两个非常特殊的角，是可以用诱导公式互化的sin π 4 +xJB））=cos π 4 －xJB）），那么

原式 ＝（（1 2 （4cos4x－4cos2x＋1） 2·（sin（（π 4 －x cos（（π 4 －x ·cos2（（π 4 －x

＝（（2cos2x－1）2 4sin（（π 4 －xcos（（π 4 －x

＝（cos22x 2sin（（π 2 －2x  ＝（cos22x 2cos2x

=（1 2 cos2x.

師：我们不能随意落笔计算，而是要在明晰运算对象的基础上，结合三角函数式的结构特点选择方法的.一般可以遵循“三看”原则：①看角之间的关系，发现 π 4 －x， π 4 +x之间的互余关系，则可化为同一个角；②看函数名称，有切有弦时，常常切化弦，化成统一形式；③看次数，次数不同时可用降幂或升幂公式化到同次，基本遵循化统一的原则.另外再结合公式的熟练度和一定的观察力，就能达到正确运算、快速解决问题的目的.

变式练习1：化简求值：（1＋cos20° 2sin20° －sin10°JB<2（（1 tan5° －tan5°

变式练习2：化简求值： sin5°－sin20°cos15° cos5°－sin20°sin15° .

教学片段2已知cos（θ＋（π 4 ＝（10  10 ，θ∈（0，（π 2 ，则sin（2θ－（π 3 ＝______.

生1：把前面的展开化简得cosθ－sinθ=  5  5 ，再和cos2θ+sin2θ=1联立方程组解出sinθ，cosθ，再解出sin2θ，cos2θ，代入最终的目标即可.

生2：换元，令t=θ+ π 4 ，反解出θ=t－ π 4 ，则已知条件是cost=  10  10 ，所求目标也用t表示，是sin 2t－ 5π 6 ，再算出sin2t，cos2t代入即可.

生3：cos2 θ+ π 4 =－sin2θ=2cos2 θ+ π 4 －1，即sin2θ= 4 5 ，再算出cos2θ，直接代入即可.

师：确实，三种方法都能算出结果，请同学们把自己选择的方法先算一算，再用其他同学的方法算一算，对比一下，然后想一想下次遇到这种问题如何处理.

师：（投影）很明显，第一种方法的运算量最大，是很直接的公式展开计算，在联立方程组计算量不算大的时候可以选择用；第二种方法是我们常说的“角变换”，“凑角”的思想，是一种全新的运算思路，并且用整体换元的方法简化了凑角的过程，提高了运算的准确性和快捷性；第三种方法比较特殊，正好已知角是θ+ π 4 ，它的二倍角正好是2θ+ π 2 ，可以用诱导公式化掉 π 2 直接得到2θ的三角函数值，运算量最小，速度最快，准确性最高.对于这题，选这种方法最好.不过如果把已知角换成θ+ π 3 ，第三种方法就不适用了，它不具有一般性，第一第二中具有一般性，一般会选第二中凑角的方法比较好.

变式练习1：设α为锐角，若cosJB（（α+ π 6 = 4 5 ，则sinJB（（2α+ π 12 的值为______.

变式练习2：已知α，β均为锐角，cosα＝（27  7 ，sinβ＝（33  14 ，则2α－β＝______.

教学片段3已知cos π 4 +θJB））= 4 5 ， 17π 12 <θ< 7π 4 ，则 1-tanθ 2sin2θ+sin2θ 的值为（）.

KG5*2 KG5*2 KG5*2 KH-1

A． 100 21

B.- 100 21

C. 75 28

D.- 75 28

本题是2022无锡市期中调研卷第7题，据统计，校均分为2.34，我所带的两个班级，分别为1.91和3.27，整体并不是很理想.所以在评讲试卷时，请同学们先说一说自己的做法.

生1：老师，您在前面强调过角变换，所以我第一反应就是先用角变换把cosθ=cos π 4 +θ- π 4 算出来，再求出sinθ，tanθ，全部带入做的，感觉也挺顺利，就是不知道哪里算错了.

师：能想到用角变换计算cosθ，很不错，节省了时间，那计算sinθ时有没有根据角的范围判断正负？还是平方出来直接取正？此方法计算量还是有的，所以一定要细心运算才行.顺便问一问，有没有同学拆出来和sin2θ+cos2θ=1联立方程计算的？举手看看（很多个同学举起了手）死算的計算量很大，易出错，费的时间也多，还影响了后面的解题.那有没有其他方法呢？

生2：我是先把后面的式子切化弦，然后用辅助角公式化简.

教师板书：

原式= 1- sinθ cosθ  2sin2θ+sin2θ = cosθ-sinθ 2sinθcosθ（sinθ+cosθ） =  2 cosJB（（θ+ π 4  sin2θ· 2 sinJB（（θ+ π 4  = cosJB（（θ+ π 4  sin2θ·sinJB（（θ+ π 4  .

生2：分子上就是题目所给的条件，分母上的sin2θ用二倍角公式cos2 π 4 +θJB））计算.

教师板书：cos2 π 4 +θJB））=2cos2 π 4 +θJB））-1=2· 16 25 -1= 7 25 .

生2：sin π 4 +θJB））用平方和等于1的解一下就行，主要是判断一下正负.

教师板书：∵ 17π 12 <θ< 7π 4 ，∴ 5π 3 < π 4 +θ<2π，∴sin π 4 +θJB））= 3 5 ，

∴原式=  4 5   7 25 · 3 5  = 100 21 .

教室里一片惊叹声！哇！有些同学说我花了二十分钟才算出来的居然这么简单！

师：生2的方法确实最简洁，把所求化到最简，然后根据条件及 π 4 +θ的特殊性，选择恰当的方法处理，快速准确地解决了问题，说明三角恒等变换中的公式已经熟练掌握并能灵活运用，节省了时间提高了运算的信心.还有不同的解法吗？

生3：我是弦化切做的，发现分母上都是二次的，再构造一个分母化成齐次式，全部化到切，然后用生1的方法把tanθ算出来代入即可.

教师板书：原式= 1-tanθ  2sin2θ+2sinθcosθ sin2θ+cos2θ  = 1-tanθ  2tan2θ+2tanθ tan2θ+1  = （1-tanθ）（tan2θ+1） 2tan2θ+2tanθ .

师：不错！生3的方法说明对弦化切的模型非常熟悉，并能用角变换的方法求解cosθ，sinθ，再求出tanθ，而不是一味的死算，很好！

对于片段1和2，是在复习三角恒等变换时讲解的，而片段3是最近考试遇到的，但可以发现，其实片段3的题不正是1和2的综合吗！可是学生对综合题的分析还是欠缺的，只顾一味地死算，做题时没有思考怎么算才是最优地，没有预判，这可能和平时地习惯有关系，平时作业多，每一道题都没有仔细地考虑就下笔算了.

3问题提升

课堂上教师要舍得留时间让学生自主探索、尝试.在这个过程中，他们可能会遇到很多困难，走很多弯路，甚至费了很多时间精力却算不下去，但是只有经历了这个过程，学生们才能在挫折中成长，找到更优的解决问题的方法，这个过程对于学生探究运算思路，选择运算方法，设计运算程序具有重要意义.三角恒等变换中的角变换往往是解题的关键，解题时需要根据已知条件去凑所求的角，若已知角只有一个，可以用整体换元的思想简化凑角的过程，若已知角有两个，可以把两个角加或减，或乘2除2再加或减去凑角，让学生从三角恒等变换的解题过程中吸取教训，总结经验，从而提升学生的数学运算能力.

课堂上教师也要舍得花时间演示计算过程，不能因为是纯计算题而不讲解了或口头说说，忽视了运算中学生会遇到的计算障碍.如2022无锡市期中调研考试第18（2）题，是个向量的计算题，很多学生卡死在了计算上，只会死算展开，就会出现高次，化不下去了，而不会一开始就把能提取公因式地先提取，我校整个年级地均分只有1.58分（总分8分）.所以教师一定要重视板书演示计算过程，慢慢渗透到学生们的心里，克服畏难运算心理，使他们发现数学运算的乐趣.

课后作业要精选，让学生对每一道题都有思考地时间，对于有难度的题，也有尝试的时间，而不是为了完成作业赶任务似的，草草看一下就做，甚至有点难度的题尝试了一下不会就放弃了.一定要让学生多思考，多尝试，多对比，才能提升数学运算能力.

数学运算是数学的“童子功”，数学运算能力的培养提升，不是一朝一夕的一日之功，而是坚持不懈的日日之功.教师课前可以用学生的思维方式去分析思考问题，尽可能的想到学生会出现哪些障碍，设计好恰当的问题串，帮学生做好铺垫，让学生在课堂上提高效率，提高学生的运算信心，进而提高学生的运算能力.

参考文献：

［1］邱婉珠.高中生数学运算素养的现状与对策研究［D］.闽南师范大学，2021.

［2］王健.例谈高中数学核心素养的培养策略——基于课堂教学中数学运算维度［J］.考试周刊，2021（99）：82-84.

［3］普通高中课程标准（2017年版）［M］.北京：人民教育出版社，2017.FL）