论学科育人的五个维度

韩继东

［摘 要］党的十八大报告明确提出，把立德树人作为教育的根本任务，这就要求各学科教师将德育放在首要位置，重视学生学科核心素养的培养。数学学科对于促进立德树人根本任务的落实有非常重要的作用，数学教师可从知识、技能、活动、思想、生活五个维度出发开展数学教学，发挥出数学学科的育人作用。

［关键词］学科育人；知识；技能；活动；思维；生活；导数

［中图分类号］    G633.6            ［文献标识码］    A          ［文章编号］    1674-6058（2023）12-0043-03

教育是一项功在当代、利在千秋的德政工程；教育是国之大计、党之大计；教育为实现中华民族伟大复兴提供了有力人才和智力支撑。“育人之本，莫如铸魂。”教师在开展高中数学课堂教学前，要进一步明确教育的根本任务，据此进行针对性教学，在教授学生数学知识的同时，也要培养学生的数学思维，发挥数学学科的育人作用。本文以“导数在研究函数单调性中的应用”为例，探究数学学科育人的五个维度。

一、知识维度

高中数学包含较多的知识，相较于中小学数学知识，其难度更大。高中数学中的导数知识既是学习的重点，也是学习的难点。导数既与函数的单调性联系密切，也涉及图象、定义域等多种知识。导数不仅在数学领域中有着广泛的应用，而且在自然科学领域的价值也不容忽视。导数的重要性不言而喻但从数学教学情况来看，很多学生不能深入了解导数的概念、函数的单调性等知识，进而无法准确地通过函数的单调性来对复杂的函数图象进行分析。针对此种情况，教师要在实际教学中强化学生对导数、函数单调性的了解，并结合具体案例，引导学生对函数图象进行观察和分析，找出函数单调性与函数图象的关系。高中生具有一定的生活经验，生活中有很多实际问题与导数、函数有直接的关系，教师引导学生分析两者之间的关系，可以帮助其解决很多数学问题。

例如，在教学“导数在研究函数单调性中的应用”时，教师可从教材知识出发，先让学生了解导数的定义，再从导数的定义出发提出问题，让学生在解决问题的过程中不断产生新的问题，最终逐步掌握导数的相关知识，为后续学习函数极值、最值知识奠定基础。

教师首先提出问题：“导数与函数的单调性有何关系？”然后出示如图1所示的函数图象，让学生观察、分析。

学生通过观察发现，如果左右移动[M]点，就可以看到[M]点在图象的增区间以及减区间的变化趋势，在此基础上进一步归结出函数[f（x）]的单调性与导数[f'（x）]的一些结论：

1.在区间（a，b）上，如果f'（x）>0，则函数f（x）在这个区间上单调递增；

2.在区间（a，b）上，如果f'（x）<0，则函数f（x）在这个区间上单调递减。

学生通过分析导数与函数单调性之间的关系，大胆猜测，严谨证明，总结出了结论，并牢固掌握了知识。

二、技能维度

在高中数学教学中，教师大多会按照一定的流程来开展教学，如分析实际问题、利用抽象思维进行数学建模、通过具体实例进行验证、得出结论、对结论进行应用和探究、对整个学习过程进行回顾与反思。在教师的引导下，学生也需要经历这样的过程，并在验证与探索中找到解题的思路，形成解题的技能。为了达到技能育人的目的，教师需要引导学生感悟解题过程，通过不断分析，总结出更多的解题方法，以此增强学生的判断能力和解题能力。

教师出示题目：运用导数知识判断下列函数的单调性。

1. f（x）=x³+3x。

2. f（x）=sinx-x，x∈（0，π）。

3. f（x）=x-1/x（x≠0）。

4. f（x）=e^x-x。

一般情况下，学生可按照以下几个步骤来进行判断：第一，对函数的定义域进行确定；第二，求出f'（x）的零点；第三，利用f'（x）的零点将函数的定义域划分为几个区域，在各个区域中分析函数的单调性。此外，教师还可引导学生画出各个原函数的图象，从图象中找到相应规律。

在解题的过程中，学生可按一般方法判断，也可先根据原函数[f（x）]画出图象，再从结论出发对问题进行解决。这样，学生便能从多角度解决问题，进而提高解题技能。

三、活动维度

著名心理学家维果斯基认为学生的发展有两种水平：一种是学生现有的水平，主要是指独立活动时所能达到的解决问题的水平；另一种是学生可能的发展水平，也就是通过学习所获得的潜力。他将学生的这两种水平之间的差异称为“最近发展区”。

要想让学生得到更好的发展，教师在教学过程中需要考虑学生的“最近发展区”，结合学生的认知水平，创设适当的教学情境，调动学生参与教学活动的积极性，让学生在具体的实践活动中体验数学知识的形成、发展过程，并获得不一样的感悟。

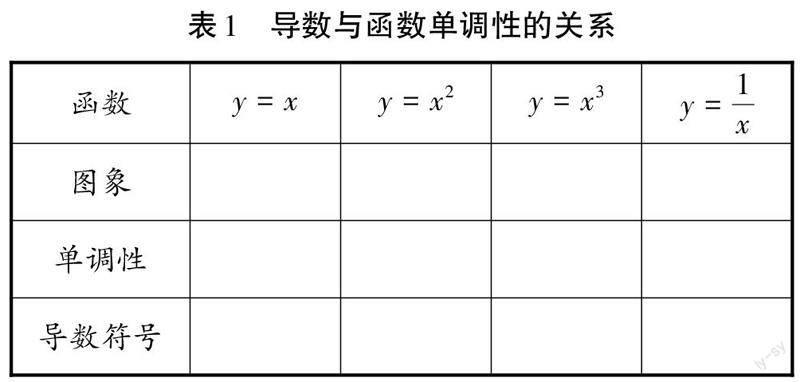
例如，在“导数在研究函数单调性中的应用”教学中，教师可引导学生以小组的形式讨论导数与函数单调性的关系。学生小组讨论导数与函数单调性的关系，并将讨论过程中的猜想填写到表格中（见表1）。教师总结导数与函数的定义，并从多角度引导学生分析导数与函数单调性之间的关系，使学生获得满意的学习成果。在合作学习的过程中，学生学会尊重自己和他人，逐步实现了自我育人、全面发展。

设计此类活动的主要目的是让学生经历数学知识从特殊到一般的推理过程，重点是让学生以合作的方式进行讨论学习，使整个学习过程更具实践性，有效促进了学生的思维发展，提高了学生的学科素养。

四、思想維度

高中数学是一门抽象性较强的学科，在高中数学教学中教师如果采用“灌输式”的教学方法，那么学生会难以理解知识，学习兴趣也会逐步降低。最为重要的是，“灌输式”教学无法突出学生学习的自主性，使学生的思维无法得到有效锻炼，这对学生学科素养的发展是不利的。

情境教学法是一种可以促进学生学科核心素养发展的教学方式。针对高中生的思维发展特点，教师可采用情境教学法进行教学，将抽象的数学问题以生动、形象的方式展示出来，让学生更加高效地学习。

例如，在教学“导数在研究函数单调性中的应用”时，教师采用情境教学法，创设了如下问题情境：“我们常将生活中的实际问题先抽象为数学问题，再通过讨论与分析问题而得到结论，那么所得出的结论是不是具有一般性特点呢？怎样对结论的正确性进行验证？”

函数外在的特点是单调性，因此在对结论进行验证时，教师可结合一些典型的问题，引导学生从导数与函数单调性的关系出发，对结论进行验证。

问题：1. f'（x）=0在某个区间上恒成立，那么此函数有什么特性？

2.已知导函数f'（x）满足下列条件：（1）当10；（2）当x<1或x>4时， f'（x）<0；（3）当x=1或x=4时， f'（x）=0，请画出函数f（x）的大概图形。

在学生得出“结论”后，教师要引导学生通过数形结合的方式来对“结论”进行验证，让学生的思维得到锻炼，使学生在不断的思维训练中找到解决方法。采用“题海战术”对学生进行训练，会增加学生的学习压力，但是以经典例题为载体，引导学生进行高效、有针对性的训练，可让学生的思维由浅层向深层递进，有利于学生发展。

五、生活维度

数学知识源于生活，又高于生活。数学知识具有逻辑性的特点，很多数学知识是通过缜密的推理而得来的。在高中数学教学中，教师应强调学以致用，要求学生将数学知识、数学技能、数学思维转化为自身的能力与素养，并在实际生活中广泛应用数学知识解决实际问题。高中数学“导数和函数的单调性”知识的学习难度较大，因此教师可贴近学生的生活创设教学情境，吸引学生参与到教学活动中，使学生学会应用数学知识解释生活现象并解决实际问题。

例如，在教学“导数在研究函数单调性中的应用”前，教师可提前下载《小猪佩奇》的动画视频，在课中给学生播放，并以有趣的案例引导学生应用数学知识分析与解决问题。教师先展示图2，然后提问：观察图片，佩奇爸爸的汽车的灯光光线有什么变化？通过观察和分析，你发现了什么数学问题？能不能根据你发现的数学问题建立数学模型？汽车在行驶的过程中，光线的变化所对应的函数图象有什么特点？

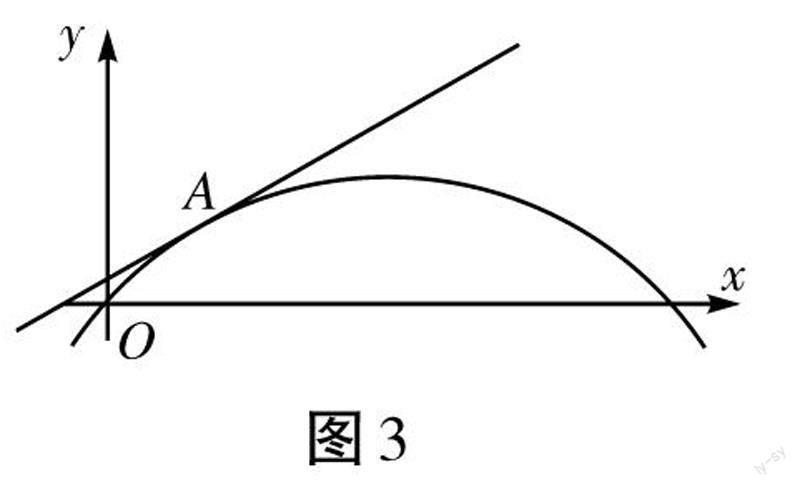
很显然，不管是结合生活实际进行观察和分析，还是从数学知识的角度进行分析，均可以发现，汽车由远及近行驶而来，车灯光线必然会发生变化，这是一个抽象的数学问题。如果将山坡看作是一个抽象函数，那么函数y=f（x）的图象在区间上的坐标图如图3所示，A点为其中一个切点，经过A点的切线可抽象为车灯光线。

在分析汽车灯光的光线变化所形成的函数的性质时，教师需要引导学生对函数图象中的信息进行提取，并结合生活中的实际问题完成数学模型的建构。观察图2可以发现，山坡的整个轮廓对应的是函数的图象，灯光光线向上運动对应的是上坡，因此函数的切线斜率[k>0]，对应函数图象递增的性质。

在上述教学中，教师以生活中的实际案例引导学生学习抽象的数学知识，让学生将生活中的实际问题与数学知识相结合，将导数与函数的单调性建立联系，分析导数与函数单调性之间的关系，激发了学生的学习兴趣，达到了生活育人的目的。

综上，高中数学函数单调性知识是学生需要重点掌握的内容，由于其包括概念、图象、定义域等多方面的内容，学习难度较大，因此学生既需要有扎实的基础知识，又需要具有较强的学习技能、思维能力等。基于此，笔者从学科育人的五个维度出发，以案例引导教学，并提出教学策略，以期提高高中数学教学质量，发挥数学学科的育人作用。

［   参   考   文   献   ］

［1］  陈骏，盛晓君.基于学科德育的高中数学教学实践与思考：以“雪花曲线的探究”为例［J］.数学教学通讯，2022（30）：3-6.

［2］  陈康，覃俊明.学科育人视角下的数学课例评析：以“抛物线及标准方程”教学为例［J］.中学教学参考，2022（5）：14-16.

［3］  华志远.以高中数学为主导的跨学科教学探索与思考［J］.数学通报，2022（6）：30-33，37.

［4］  张晓斌，米新生，陈昌浩，等.高中数学“函数的概念与性质”主题内容教学探究［J］.教学与管理，2022（30）：87-90.

［5］  施惠芳. 数学学科完整育人视域下的完整学习［J］. 中国教育学刊，2021（6）：104.

（责任编辑    黄春香）