基于加权灵敏度的某天线座结构优化设计

杨罡星 刘 珺

(湖南航天环宇通信科技股份有限公司 长沙 410000)

0 引言

随着无线通讯技术的发展,天线口径不断增大、工作波段不断提高,对天线的电性能提出了更高的要求。天线座是雷达系统中较为重要的一部分,可以实现天线的运转、定位、定向等功能,而天线座结构的刚度直接影响着整个雷达系统的控制精度。以传统的设计经验为驱动的试错法存在着设计周期长、设计成本高等缺点,很难满足日新月异的天线结构设计要求。因此,本文提出了一种快速高效优化方法可以用于解决此问题。在天线座的优化设计方面,蒋旻等[1]使用参数化建模。从散热设计和工艺性出发,实现了天线座结构改进,该方法可操作性强,但仅局限于目标单一的结构优化。郑鸿生等[2]利用有限元分析了某雷达座的刚强度,并利用Design Exploration对整体结构进行了优化。房建斌[3]采用协同优化方法,对天线座造型优化、约束优化以及结构构型优化设计,在较短时间内取得满意效果,使力学性能得到大幅提升。付佐红[4]对桁架式天线座的精度和刚度不足进行优化研究,但同样存在问题诊断困难等问题。赵德高等[5]利用非支配遗传算法(nsga-ii)求解了某天线座多目标优化问题,并对其提出了改进,利用改进算法解决了车载雷达天线座设计的多目标设计优化。而对于灵敏度优化分析方面,葛悦[6]等考虑分离安全性的运载火箭卫星舱壳体设计,对各分区参数进行了灵敏度分析,优化后提高了火箭的有效载荷运载能力。本文基于设计灵敏度,并利用质量对其加权,对某固定站天线座的刚性不足问题进行快速定位,并对天线座薄弱的地方进行加强,用较短时间完成了产品的优化迭代。

1 优化理论

在优化设计中,通常有三要素,即设计变量、目标函数与约束条件。设计变量指结构设计中的各种使结构性能发生改变的变量;设计约束是对变量的约束,是对设计变量和其他性能的边界条件。目标函数要求求解设计性能的最值,是关于设计变量的函数。对于正优化问题,优化过程如图1所示。

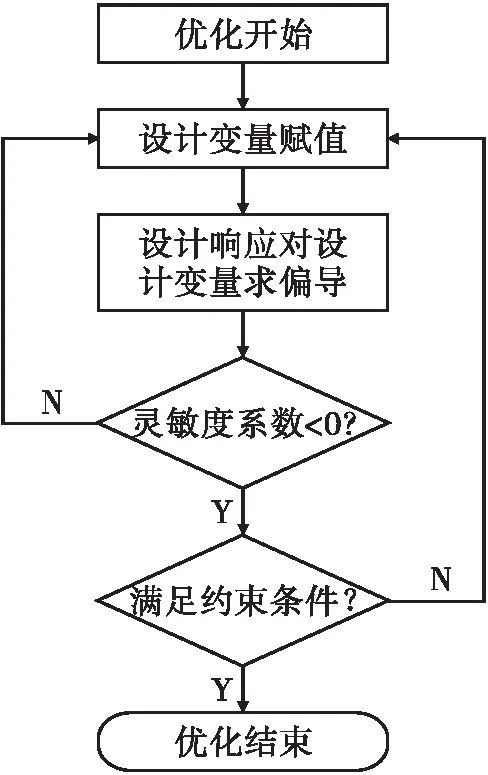
图1 优化设计流程

而设计灵敏度是关于设计响应对优化变量的偏导数。对于静力分析,有限元求解方程可写为

[K][U]=[P]

(1)

此时可使方程两边对第i个设计变量Xi求偏导得

(2)

则式(2)可写成

(3)

等式(3)左边即为一阶位移灵敏度,但通常设计变量控制中,变量一般也设为应力,体积分数等其他变量,因此,应将位移响应转换为其他静力响应,于是可将第i个设计变量对第j个响应的灵敏度系数表示为

(4)

其中:[K]为总体刚度矩阵;

[U]为位移列向量;

[P]为载荷列向量;

Xi为第i个设计变量;

ri,rj为第i,j个响应。

由此可知灵敏度代表着变量-响应曲线中的斜率,灵敏度为正,响应随变量增加而增加,灵敏度为负,响应随变量增加而减小,灵敏度绝对值越大,更改变量时响应变化得越明显。但应注意的是优化过程中存在的“非凸”问题,即在优化区间内响应存在多个最值,因此,本文采用基于全局优化算法的灵敏度分析,可保证在区间内可以找到最优解。

2 某天线座的灵敏度分析

利用有限元技术分析某天线座的抗风力学性能。天线座由基座、方位转台、俯仰转台三大结构组成,每部分结构由加强筋,筒壁,法兰边拼焊而成。反射面通过螺栓安装在俯仰臂上,材料为Q355b结构钢,其参数如下:密度为7850kg/m3;弹性模量E=200GPa;泊松比为0.3;屈服强度σs=345MPa。在天线座轴系误差分析中,仅由天馈子系统重力或风载导致机械轴的偏差非常小,因此本文不考虑反射面等的影响,仅考虑天线座自身的两轴误差,将反射面部分等效为刚体,通过耦合约束在俯仰臂上,只传递风力和施加重力载荷,作用点为反射面顶点。

本天线座工作在Ka频段,工作精度要求8级风正常工作,风载计算由式(5)、式(6)给出

F=CF·A·q

(5)

M=CM·A·D·q

(6)

其中:CF为风力系数,CM为风力矩系数,由风洞实验测量给出[7],见表1所示。

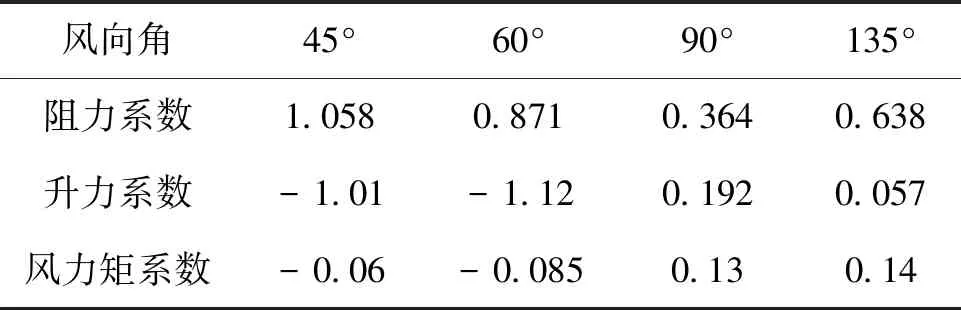
表1 各风向角风力系数

q为动压,计算公式为

(7)

其中:ρ为空气密度,一般取1.25kg/m3;v为风速,8级风取21m/s,可计算出q=275.6Pa;A为天线口径面积,本天线座为41.8m2;D为天线口径,本天线座为7.3m;其中风力和风力矩的作用点均为天线反射面顶点。天线座的有限元模型如图2所示。

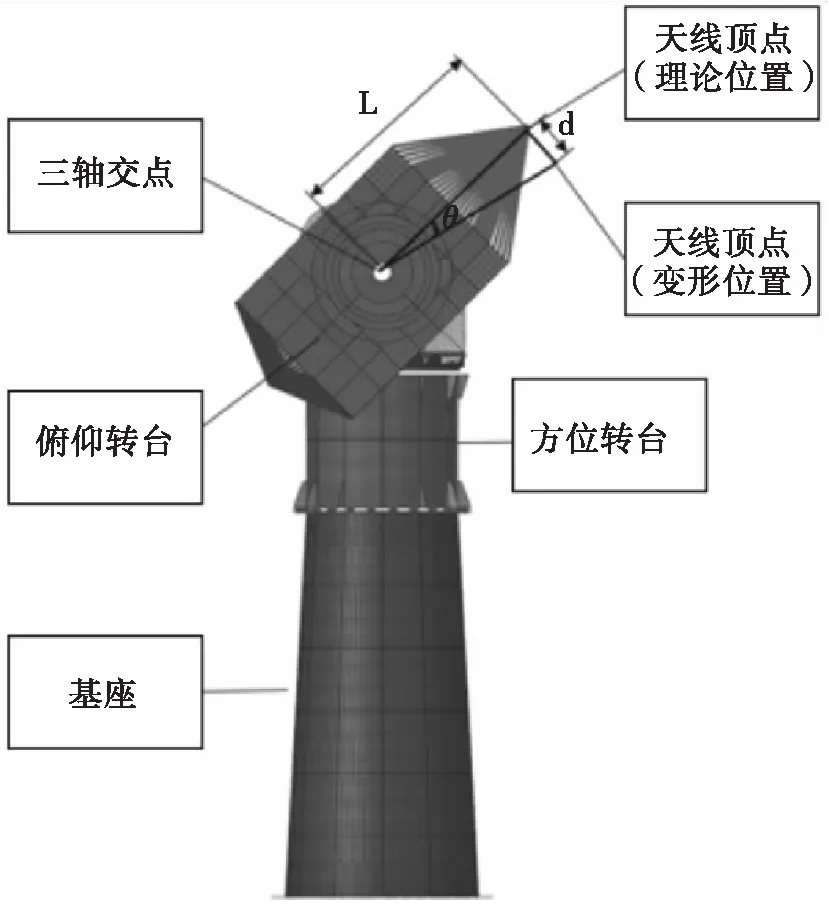
图2 天线座有限元模型

对此模型分析了天线座的四种不同风向角下的工况:

工况一:重力、风向角45° 8级风压;

工况二:重力、风向角60° 8级风压;

工况三:重力、风向角90° 8级风压;

工况四:重力、风向角135° 8级风压。

通过式(5)、式(6)可计算出天线各载荷如表2所示。

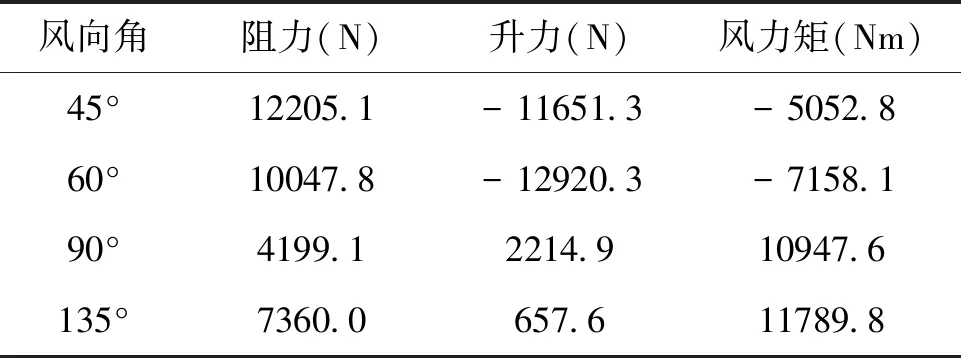
表2 各工况风力计算结果

其中阻力与风速同向为正,升力竖直向上为正,风力矩绕俯仰轴逆时针为正。

本天线座伺服系统自跟踪精度要求≤1/10波束宽度,误差分解包括单脉冲测量误差、制造装配误差、轴角测量误差以及载荷变形误差。其中各个误差又可分解为各轴系误差,本文对此不作过多探讨,仅以有限元模型后处理中的指向角度偏转作为最终各轴系误差的合成[8]。实际计算中指向角度变化一般很小,因此可通过反射面顶点与三轴交点的空间位置关系换算出:

(8)

见图2所示,其中θ为偏转角度;d为反射面顶点位移,通过仿真分析得出;L为反射面顶点到三轴交点的距离(本天线座为1486mm)。

通过误差分解,分配到载荷变形的偏转角度为0.02°,反计算后得出反射面顶点位移应小于0.52mm才能满足伺服控制精度要求。

变形云图如图3所示,应力云图如图4所示,分析结果如表3所示。

表3 各工况顶点位移

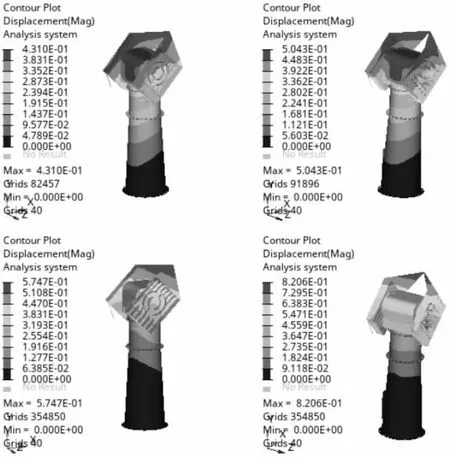
图3 天线座风载变形云图

图4 天线座风载应力云图

结合结果和上文分析可知,原有结构不满足伺服控制精度要求,此时仅通过云图难以判断结构的弱点,可利用灵敏度分析快速诊断结构的弱处。

基于此天线座结构,可将各零件的弹性模量或均一单元密度作为变量。综合考虑,本文以各零件包括筒壁,加强筋,法兰边的弹性模量作为设计变量,灵敏度计算完成后可根据灵敏度大小排序进行相应零件的优化。

以体积分数、各零件强度及四种工况的反射面顶点位移作为约束。其中工况一、二已满足要求,但为了避免优化其它工况过程中对工况一、二的减弱,因此也将其分析在内。优化过程中,应力较小,不考虑强度约束,以此增加优化收敛性,以最终设计方案作为强度校核。

以四种工况的加权柔度为目标,柔度可近似视作刚度的倒数。同理也考虑了工况一、工况二的影响。综合考虑柔度权值为:1∶1∶2∶4。

3 加权灵敏度后处理及优化

利用有限元优化方法可分析各零件灵敏度,对于稳态线性问题,结构响应与设计变量的关系一般也呈线性,因此只需取迭代第一步的灵敏度系数为参考结果,可以达到设计优化。由于一些零件如基座筒壁、方位筒壁相对于法兰边、加强筋较厚重,因此可利用各零件的质量对灵敏度进行加权。这样可使优化性价比达到最高。

表4列出了分析中的质量加权灵敏度系数。表中为柔度对各零件的弹性模量灵敏度系数,按第1节理论分析可知,考虑负值时,灵敏度绝对值越大代表该零件越需要加强。由此进行排序,对灵敏度绝对值较大的零件进行增厚,筋增高、加筋等优化,对灵敏度绝对值较小的零件进行减薄,筋降低等改进。

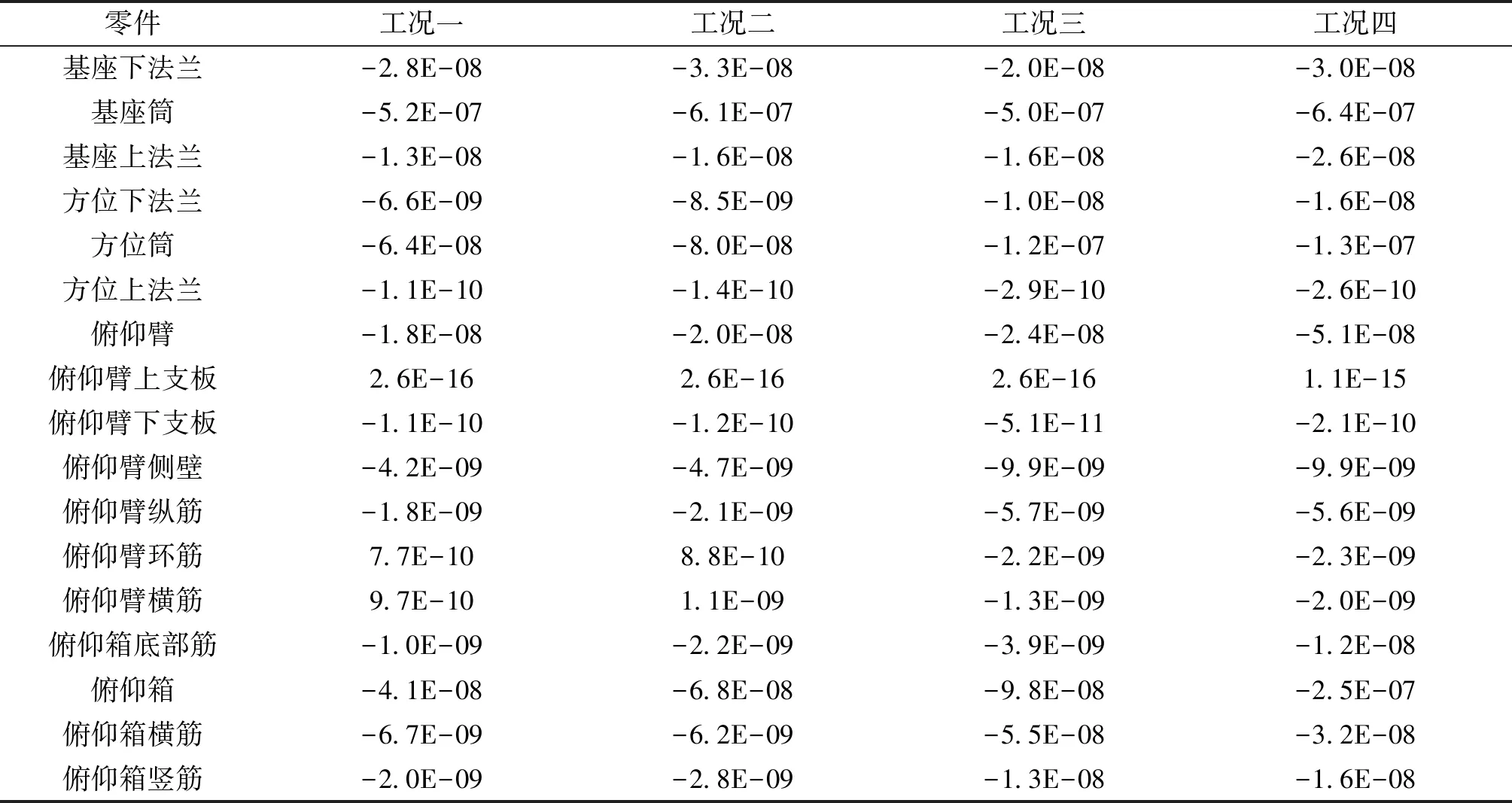
表4 天线座各零件质量加权灵敏度

另外观察表4发现:虽然已用质量进行加权,基座筒的灵敏度对比其他零件仍较大,说明基座刚度对精度控制贡献极大,但此时强度余量较多,直接加厚基座筒壁,相对缺乏经济性。可进一步对基座筒基于工况一至四进行拓扑优化,在内壁生成加强筋及增加法兰斜撑板,同时适当减小基座筒壁厚,达到设计最优。经过52个迭代优化步,拓扑优化单元密度分布如图5所示。

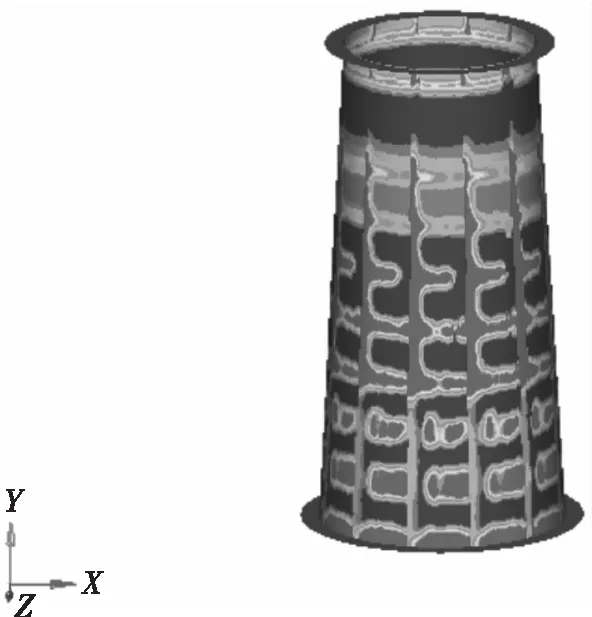
图5 基座单元密度分布

图中暗色区域代表优化后单元密度大的区域,即需要加强的区域,黑色区域代表优化后单元密度小的区域,即可以适当减薄的区域。拓扑优化的结果云图不能直接使用于具体的工程设计,必须对拓扑优化结果进行综合考虑,提取拓扑特征进行重构,通过构建重构模型的有限元模型,对新的模型进行加强筋的布置优化,最终得到新的设计模型,用于工程实际,如图6所示。

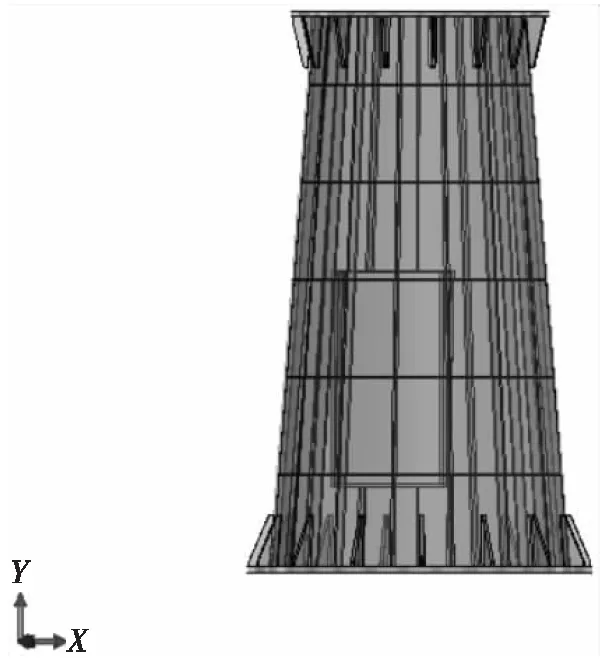
图6 基座拓扑优化设计

综合灵敏度分析及拓扑结果,通过对灵敏度绝对值较大的零件进行增厚,筋增高、加筋等优化,对整体结构进行了一些改进,优化结果如图7所示,图8所示,各结果对比如表5所示。

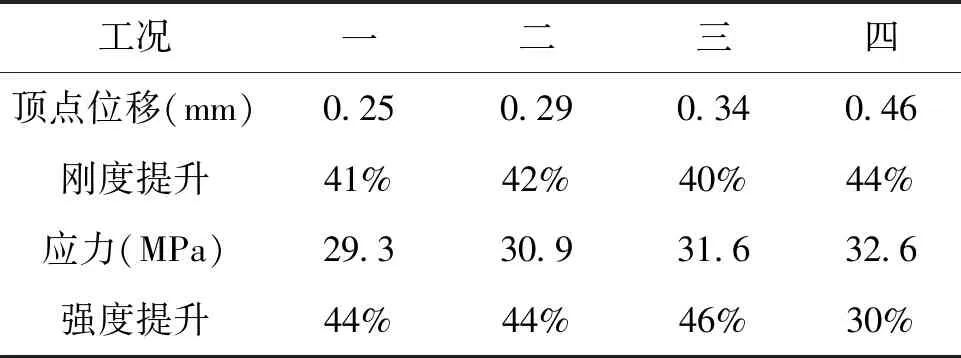
表5 各工况优化后顶点位移

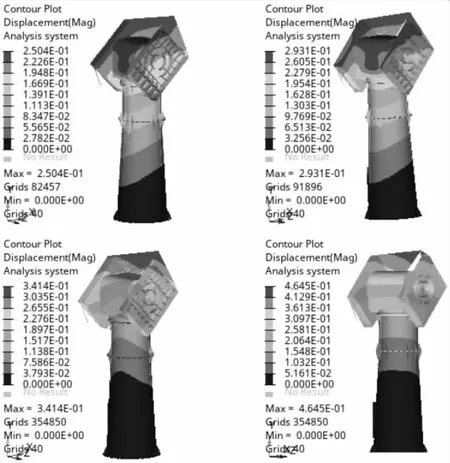
图7 各工况优化后变形云图

图8 各工况优化后应力云图

与最初的设计方案相比,工况一顶点位移由优化前0.43mm降为0.25mm,刚度提升41%;工况二顶点位移由0.50mm降为0.29mm,刚度提升42%;工况三顶点位移由0.57mm降为0.34mm,刚度提升40%;工况四顶点位移由0.82mm降为0.46mm,刚度提升44%。优化后,工况一至四均满足控制系统对转台刚度的要求,且优化后强度满足要求。

4 结束语

本文提出了一种基于加权灵敏度的天线座结果优化方法。该优化方法利用优化理论,计算出各个零件的灵敏度,通过筛选灵敏度排序,可快速定位对目标函数而言中刚性不足的结构,对各零件进行系统性的优化,对目标函数贡献极大的结构,可针对性地进一步进行拓扑优化等优化手段,大大减少了设计成本,提升了设计效率。基于此方法,对某天线座进行了灵敏度诊断及优化,通过对天线座各个零件的重新优化设计,优化后各分析工况的刚度提升40%以上,使天线座刚度满足控制系统要求,且强度仍满足一定的裕度。优化后的天线座已投产使用,在标校标定及实际使用过程中,未出现指向跟踪控制问题,证实了本方法的正确性,对今后的天线座结构优化设计具有一定的指导和借鉴作用。