双反射面天线装配过程中同轴度误差分析
孙瑞峰 朱士琦 刘兰波 苏永胜 陈敏豪
双反射面天线装配过程中同轴度误差分析
孙瑞峰 朱士琦 刘兰波 苏永胜 陈敏豪
(上海航天电子技术研究所,上海 201109)
分析双反射面天线在装配过程中主、副反射面的同轴度,利用位姿矩阵表示主、副反射面的同轴度,得到同轴度与转角的关系方程。通过Mathcad软件根据关系方程生成转角与同轴度的等值线图,确定不同位置的转角对同轴度的影响,提高了主、副反射面装配的同轴度精度,缩短了装配的周期。
双反射面天线;同轴度;尺寸链;位姿矩阵

1 引言
随着通信、雷达、人造卫星的发展,反射面天线有着越来越广泛的应用,在众多类型的反射面天线中双反射面天线具有效率高、噪声温度低,能量分布均匀,而且馈源可安装在主反射面后部,可减小馈线损耗带来的不利影响,常常被选择作为收发射天线。如图1所示,双反射面天线由主反射面、副反射面和馈源组合而成。馈源安装在副反射面的实交点1上,主反射面的焦点与副反射面的虚焦点2重合[1]。由于主反射面与副反射面的焦点重合,馈源发出的电磁波经主、副反射面的两次反射后,辐射平行于主反射面的法线方向。在主、副反射面装配时主、副反射面的相对高度和同轴度对主反射面的焦点与副反射面的焦点重合程度有很大的影响,进而影响天线的电性能。

图1 双反射面天线
2 利用换面法对同轴度分析
目前双反射面天线在主、副反射面的装配过程中,为保证主、副反射面的同轴度及相对高度,通常使用装配工装辅助装配,如图2所示。装配时先将主反射面与工装底座配合,形成同轴度误差1;然后将工装端板装入工装底座,形成同轴度误差2;副反射面与工装端板配合,形成同轴度误差3。
主、副反射面及工装的轴线实际是空间分布的,如采用换面法分析,即将空间尺寸链转化为平面尺寸链的计算方法。如图3所示,将各轴线转化到同一平面上。则主、副反射面的同轴度误差4与1、2、3组成装配尺寸链,其中主、副反射面的同轴度误差4为封闭环。

图2 主、副反射面装配过程示意

图3 主、副反射面尺寸链
根据转换到同一平面后形成的尺寸链,以及装配尺寸链的计算原则,得到主、副反射面同轴度为:
4=1+2+3(1)
换面法计算思想比较简单,但很难采用换面法建立尺寸链及尺寸链方程。同时换面法不仅需要研究集合元素之间的相对关系和这些元素与投影面之间的相对位置,还需要研究如何选择新投影面以及集合元素在新投影面体系及原投影体系中投影之间的关系[2]。作图复杂,误差较大,无法对主、副反射面同轴度的调整提供有效的依据。
3 同轴度坐标系建立
3.1 位姿矩阵原理
在主、副反射面的装配过程中装配工装与主反射面及工装各零件之间的同轴度传递到副反射面,造成副反射面轴线与主反射面的轴线发生偏离。因此装配过程中各零件同轴度误差的传递通过位姿矩阵传递比较方便,几何意义也比较明确。
位姿矩阵是利用4×4方阵同时把新坐标系在参考坐标系中的位置和姿态表示出来,即:

在式(2)中,为姿态矩阵,即新坐标系相对于参考坐标系的方向余弦阵,是3×3的方阵;为新坐标系中点的向径在该坐标系下的表示,是3×1矩阵。根据位姿矩阵的定义,新坐标系绕参考坐标系、、坐标轴的相应旋转变换矩阵可表示为:



位姿矩阵一个重要特点是不但可以描述两个物体的旋转变换,而且可以描述物体运动的平移变换[3],新坐标系相对于参考坐标系的平移矩阵如式(6)所示。

由于新坐标系可认为是参考坐标系通过旋转和平移产生,所以新坐标系相对于参考坐标系的位姿矩阵为旋转变换矩阵与平移矩阵的点乘,如式(7)所示。

3.2 位姿矩阵对同轴度的求解
为利用位姿矩阵表示主、副反射面的同轴度,需要建立一系列的坐标系,通过各坐标系之间的位姿关系得出主、副反射面之间的同轴度。以各零件的轴线为轴建立坐标系,轴的方向与测量时的三坐标测量坐标系中的轴方向一致,轴由右手定则确定。如图4所示,0000为主反射面轴线坐标系、1111为工装底座轴线坐标系、2222为工装支撑块轴线坐标系、3333为副反射面轴线坐标系。

图4 坐标系示意
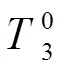

通过式(8)得到的位姿矩阵可以得到副反射面中的任意点在主反射面坐标系0000下的点坐标。在主副装配过程中,需要保证副反射面轴线相对于主反射面轴线的位置,因此需要得到副反射面轴线在主反射面坐标系0000下位姿,即将主、副反射面之间的同轴度求解转换为坐标系的位姿求解。
实际情况下由于装配工装的限制,所建立的各坐标系不能相对于所参考坐标系的轴与轴移动和旋转,只可以绕其参考坐标系中的轴旋转,旋转的半径为零件之间配合所产生的同轴度,因此可以将各坐标系投影到主反射面坐标系的000平面内,如图5所示。坐标系在其参考坐标系下的姿态矩阵为rot(,),而坐标系相对于参考坐标系的位移矩阵trans(P,P,P),则利用同轴度及坐标系相对于参考坐标系的旋转角度分解到参考坐标系的轴与轴确定。在000平面内对主、副反射面同轴度的求解即可转化为对坐标系3333与坐标系0000原点间的距离求解。

图5 坐标系在O0X0Y0平面投影
在000平面内,根据式(7)可以得到工装底座轴线坐标系1111在主反射面轴线坐标系0000下的位姿矩阵为式(9),式中,1为工装底座轴线坐标系1111绕主反射面轴线坐标系0000中轴的转角,1为工装底座与主反射面配合后的同轴度;工装支撑块轴线坐标系2222在工装底座轴线坐标系1111下的位姿矩阵为式(10),式中,2为工装支撑块轴线坐标系2222绕工装底座轴线坐标系1111的中轴的转角,2为工装支撑块与工装底座配合后的同轴度。

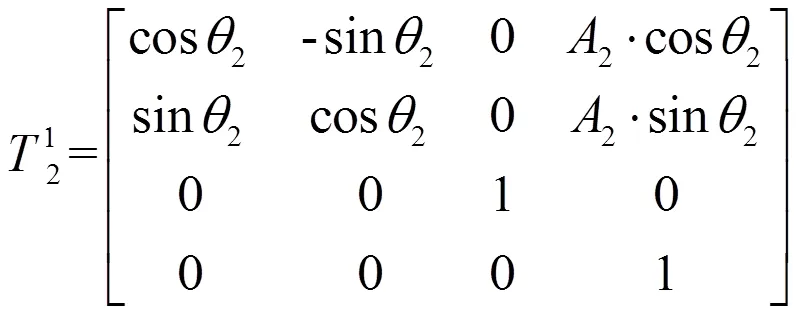
通过副反射面与工装支撑块的同轴度3及相对与3的转角3向2轴与2轴投影,得到副反射面坐标系3333的原点在工装支撑块轴线坐标系2222下的坐标点。为便于利用位姿矩阵计算,将该坐标点表示成4×1矩阵的形式,如式(11)所示。矩阵的第一行和第二行分别对应副反射面坐标系O3X3Y3Z3的原点在工装支撑块轴线坐标系O2X2Y2Z2下的X2轴与Y2轴坐标点。

则副反射面坐标系3333的原点在主反射面坐标系0000下的点坐标矩阵位姿矩阵如式(12)所示。



主反射面与副反射面的同轴度4即副反射面坐标系3333的原点与主反射面坐标系0000原点的距离为:

以430mm口径的双反射面天线为例,工装底座轴线相对于主反射面轴线的转角θ1对主、副反射面的同轴度不会产生影响,为简化计算取θ1=0。工装端板相对于工装底座的转角θ2取值范围-180°~180°,副反射面相对于工装端板的转角θ3取值范围-180°~180°。将数据代入式(15),利用MathCAD软件得到主、副反射面的同轴度等值线图,如图6所示。通过同轴度等值线图可以得到不同角度所对应的主、副反射面的同轴度,在实际的装配过程中可根据同轴度等值线图调整主、副反射面及工装的角度,进而使同轴度达到要求。
4 结束语
通过位姿矩阵对主、副反射面在装配过程中的同轴度进行表示,将同轴度的求解转换为对坐标系之间的位姿矩阵的求解,并建立主、副反射面的同轴度与各零件之间转角的关系方程,通过MathCAD软件得到主、副反射面的同轴度等直线图。利用等值线图可直接得到不同的转角对应的同轴度,在保证同轴度的同时,简化装配过程中的调整,提高了装配的效率。
1 钟顺时. 天线理论与技术[M]. 北京:电子工业出版社,2015
2 彭翠芳. 图解空间几何问题的一种旋转换面法[J]. 南昌大学学报,2001,23(4):53~56
3 任顺青,陈希军,王常虹. 惯导测试设备的检验及试验技术[M]. 北京:科学出版社,2017
Analysis on Coaxiality Error of Dual Reflector Antenna in Assembling Process
Sun Ruifeng Zhu Shiqi Liu Lanbo Su Yongsheng Chen Minhao
(Shanghai Aerospace Electronic Technology Institute, Shanghai 201109)
Analysis on the coaxiality of the primary and secondary reflective surfaces of the dual reflector antenna during the assemble process, and the coaxiality of the primary and secondary reflective surfaces is expressed by the D-H matrix, and the relationship equation between the coaxiality and the rotation angle is obtained. Mathcad software is used to generate contour maps of rotation angle and coaxiality according to the relationship equation to determine the influence of rotation angles at different positions on coaxiality, which improves the coaxiality accuracy of the main and auxiliary reflecting surface assembly and shortens the cycle of assembly.
dual reflector antenna;coaxiality;dimension chain;D-H matrix
孙瑞峰(1990),硕士,机械制造及其自动化专业;研究方向:精密装配工艺。
2020-09-03

