基于DBSCAN聚类和曲线拟合的PRI分选算法

常安琪 乔宏乐 徐 伟

(西安电子工程研究所 西安 710100)

0 引言

PRI分选的本质是对信号到达时间(Time Of Arrival,TOA)的去交错处理。1989年,H.K.Mardia在基于序列搜索法和统计直方图法的基础上提出了累积差值直方图法(CDIF)[1],具有一定的抗脉冲丢失性能,但计算量较大; 1992年,Milojevie等人在改进和完善累积差直方图法的基础上提出了序列差值直方图法(SDIF)[2],该方法在运算速率和防止虚假目标方面均有较为显著的提升。 1993 年 Nelson 提出了经典的 PRI变换算法[3],可较好地抑制直方图中的谐波分量,但抗抖动效果较差。近些年的PRI分选处理除了在上述经典算法基础上进行改进以外,也越来越多地引入了聚类算法,如2007年国强针对未知辐射源信号的预分选提出了 K-means 聚类算法与支持向量聚类算法[4]等等。

本文分析对照了基于DBSCAN聚类和曲线拟合的PRI分选算法和基于SDIF的PRI分选算法。与常用的Kmeans聚类相关算法比较,DBSCAN聚类算法亦具有以下优势:一是不需要输入划分聚类的个数;二是聚类簇的形状没有偏倚(K-means适用于球形类数据簇);三是可以在需要时输入过滤噪声的参数。与传统的PRI搜索算法比较,曲线拟合可以有效降低野值点的影响,提高正确分选效率。

1 DBSCAN聚类

DBSCAN(density based spatial clustering of applications with noise)[5]算法是一种典型的基于密度的聚类方法,可以发现任何形状的簇,具有良好的噪声识别性能。其工作原理是根据预设密度阈值确定划分为某一个类的数值门限,将密度足够高的区域进行聚类。

DBSCAN具体算法流程如图1所示。

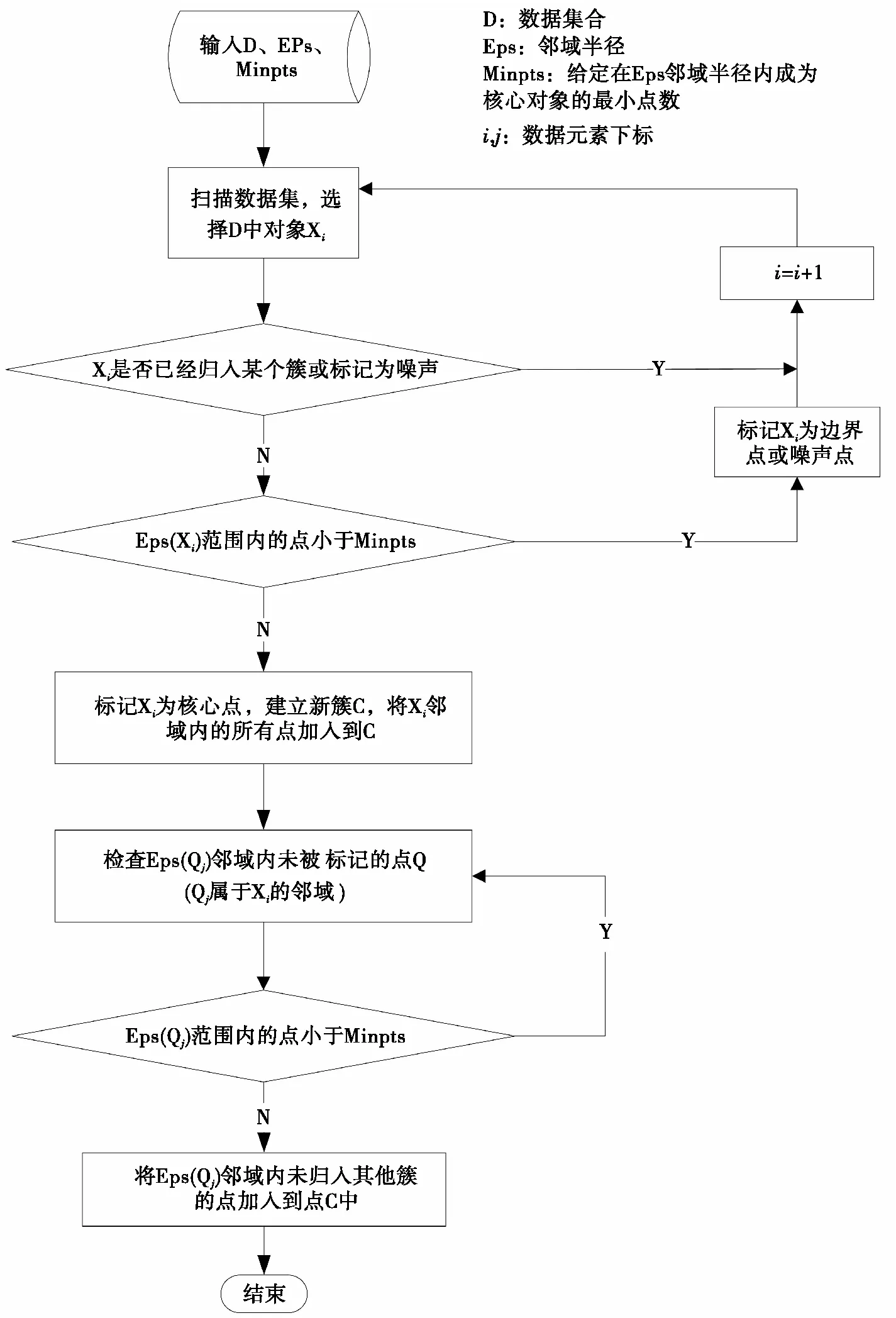
图1 DBSCAN聚类算法流图

在输入数据集之前,DBSCAN算法需要确定两个核心参数,Eps邻域半径及MinPts 阈值门限,即给定在Eps邻域半径内成为核心对象的最小点数。如图1所示,D表示待分类的数据集,i、j表示数据集D中的元素下标。其中,Eps的选取将会对聚类效果会产生很大影响。Eps选择过小,众多数据难以正常聚类,被识别为异常点;Eps选取过大,总体聚类类别数减小,异常点无法识别且聚类效果差[6]。

Eps和MinPts的值可根据工程的实际需求确定。例如,假设工程所需PRI识别精度为1μs,则可给定邻域半径Eps为1μs。在Eps确定的情况下,可统计数据集中每个点的Eps领域内点的个数,通过对全数据集中每个点对应该数值求数学期望得到MinPts[7],此时MinPts为每个聚类中核心对象Eps内数据点个数的最优值。MinPts的计算公式为

(1)

其中,pi为点i的Eps领域内点的个数。

2 PRI分选

基于PRI的雷达信号分选通常分为两个步骤,第一个步骤是对目标雷达信号的PRI进行估计;第二个步骤是根据估计出的PRI值在混叠脉冲序列中进行序列搜索,提取出该PRI值对应的所有脉冲序列。

2.1 基于密度聚类的PRI值估计算法

假设TOAn(n=1,2,…,N)表征脉冲到达时间序列,那么TOA1表示第 1 个脉冲的到达时间,TOAN表示第N个脉冲的到达时间。那么对脉冲序列到达时间进行三级差值处理可得:

Arr1=TOA2-TOA1,…,TOAN-TOAN-1

(2)

Arr2=TOA3-TOA1,…,TOAN-TOAN-2

(3)

Arr3=TOA4-TOA1,…,TOAN-TOAN-3

(4)

将上述三式叠加可得:

Arr=Arr1+Arr2+Arr3

(5)

以三组脉冲重复间隔值分别为PRI1=187、PRI2=230、PRI3=300为例,噪声水平为10%,混叠到达时间(TOA)序列的三级差值序列图如图2所示。

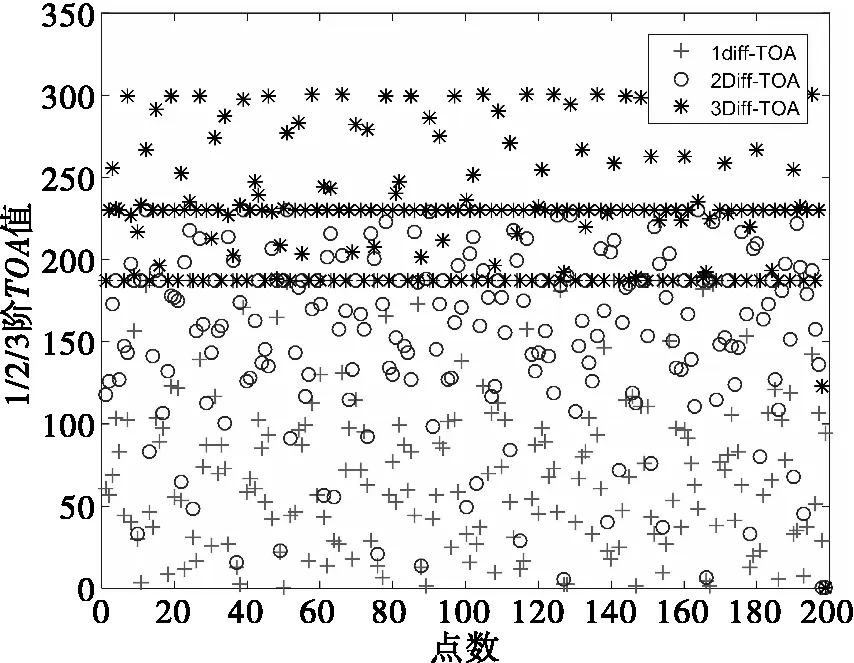
图2 一/二/三阶TOA差值分布图

如图2所示,数据点在187μs和230μs处呈现出明显的聚集状态,因此可以通过基于密度的聚类方式对TOA序列差值进行处理。

在同一电磁环境下,Eps的取值可以通过事先使用实测信号进行预聚类,观察聚类结果来确定。根据DBSCAN聚类输入参数选取原则,邻域半径Eps=1μs,阈值门限MinPts=6length(Arr)/max(Arr),采用该参数进行噪声剔除可得聚类结果如图3所示。

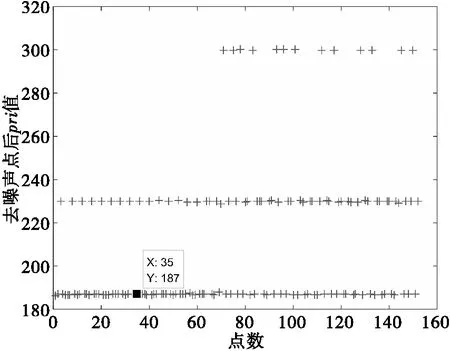
图3 第一轮聚类PRI值分布图

通过图3可得,第一轮中需要被提取的PRI值为187μs。将PRI=187μs所包含的到达时间序列通过后文2.2节曲线拟合进行提取之后,继续重复该聚类算法可得图4和图5。

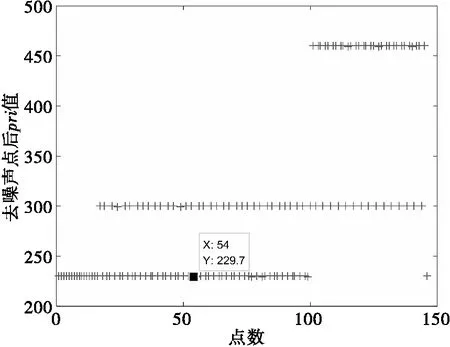
图4 第二轮聚类PRI值分布图

如图3～图5所示,在不同PRI值序列的提取过程中,选取数据点分布最多的类对应的均值作为PRI估计值,该PRI值必然周期较短,且对应的脉冲序列出现的频率较高,因此可以将个数最多的脉冲序列从混叠时间序列中提取出来,从而降低原始脉冲流密度。再对剩余的时间脉冲序列重复上述PRI估计和提取的过程,每次只提取一组脉冲序列,直到没有足够的脉冲点可供分选。即完成了对混叠序列的PRI值估计。

2.2 基于曲线拟合的PRI值提取算法

PRI曲线拟合的算法原理是:如果一个理想的雷达脉冲信号具有恒定的脉冲重复周期(PRI),那么各脉冲的到达时间(TOA)与脉冲到达序号(基准脉冲间隔的PRI个数)间呈现一维线性关系。设横坐标x为雷达各脉冲序号,纵坐标y为雷达脉冲的到达时间,对应直线方程为

y=kx+b

(6)

其中斜率k代表雷达信号的脉冲重复周期,截距b则代表初始脉冲的到达时间。

传统的曲线拟合算法(LMS)依据的原理是点到直线的距离是否满足最小容差,但运算量非常大,不利于进行实时处理。改进型的PRI曲线拟合依据的原理是:通过斜率值PRI和截距值到达时间(toa)初始值,来预估第i个到达时间理论值,并判断其与实际TOA的差值是否满足最小容差,具体方法如式(7)所示。

假设某雷达第i个脉冲的到达时间为TOAi,则

TOAi-TOA0=i×(PRI+∇t/i)

(7)

因此

(8)

假设已经求出了前i-1个脉冲对应PRI的期望值,则第前i个脉冲PRI的期望值通过式(9)计算得

(9)

本文所采取算法与传统曲线拟合公式不同,加大了新元素的拟合占比,仿真实验验证,分选正确率更高。同理,假设已求出了第i个脉冲以前的曲线拟合截距b,则第i+1个脉冲b的期望值方法采用如式(10)、式(11)方式计算:

b′i=TOAi-PRIi×i

(10)

(11)

改进LMS算法不仅在性能上与经典的LMS算法相差无几,而且在时间上比经典的LMS算法省去将近1/3的时间,使整个系统具有更好的实时性,降低计算单元的负担。

基于曲线拟合的PRI搜索算法,基本原理是确定一个初始到达时间,也称为基准脉冲,根据潜在的PRI值进行序列搜索,若搜索得到的脉冲数超过既定门限,则可匹配找到该值对应的到达时间序列值,本文中具体步骤如下:

1)步骤1:根据DBSCAN算法得出潜在PRI值。

2)步骤2:以初始到达时间为基准,计算下一个相邻脉冲与基准值的一级差值作为可能的PRI值,判断其与真实PRI的差值是否在误差允许范围内,若满足条件,则继续通过该值进行搜索;若不满足条件,则以下一个相邻脉冲为基准,继续计算判断。

3)步骤3:若通过步骤2搜索到的脉冲数目大于8个,则认为潜在的PRI值为真实的PRI值,按照该PRI值进行曲线拟合。否则计算第三个脉冲与基准的二级差,继续重复上述判断,直到可能的PRI值不在真实PRI值的误差允许范围内,基准脉冲换为下一个相邻脉冲。

4)步骤4:重复步骤2、步骤3,直到无法找到满足条件的基准脉冲或剩余脉冲数目不足。

如图6所示,是经过第一轮PRI抽取的到达时间序列图,圆圈标注的采样点即为从原始混叠到达时间序列中和当前PRI匹配的TOA值;图7是对抽取出的TOA序列值进行曲线拟合的结果,可以得出其符合相应的一维线性关系。

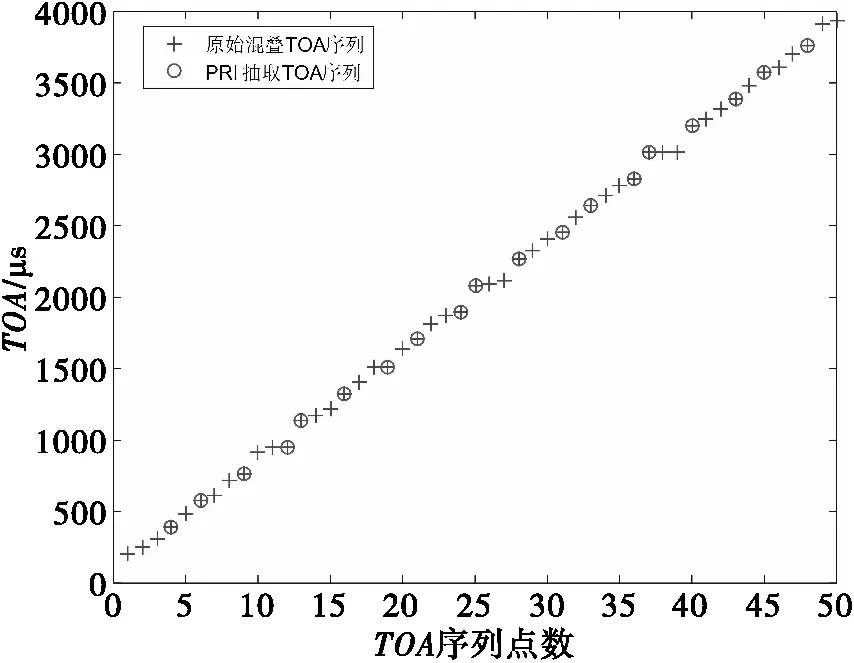
图6 第一轮抽取到达时间(TOA)序列图

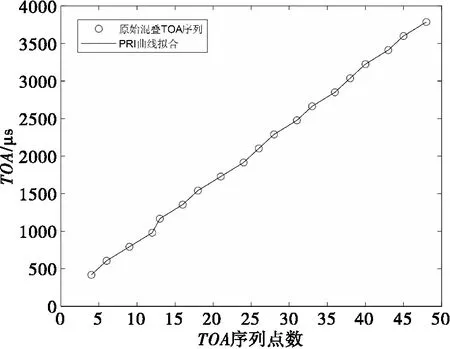
图7 曲线拟合到达时间序列图

3 对照仿真实验

为了对照本文所提出的基于DBSCAN聚类和PRI曲线拟合的PRI分选算法和经典SDIF分选算法之间的性能差异,采取单一变量对照试验,分别对不同待分选信号个数、不同噪声系数下两种分选算法的分选正确率进行统计,蒙特卡洛循环次数均为1000次,对照试验条件如下:

1)仿真实验1:

待分选信号源个数radarNum=2, radarNum=3,radarNum=4,脉冲重复周期值分别为:①PRI1=187、PRI2=230;②PRI1=187、PRI2=230、PRI3=300;③PRI1=187、PRI2=230、PRI3=300、PRI4=410;到达时间噪声为均匀噪声,噪声水平为20%,正确率对照试验结果如表1所示。

表1 不同信号源个数条件下两算法分选性能对照表

结论:由实验对照表1可以看出,在固定噪声水平、不同信号源个数的条件下,DBSCAN聚类加曲线拟合的方法的分选正确率优于基于统计直方图的SDIF算法,在多信号(四信号源)条件下更为明显,说明文中所提办法对复杂多信号环境的适应性更强。

2)仿真对照实验2:

待分选信号源个数radarNum=3脉冲重复周期值分别为:PRI1=187、PRI2=230、PRI3=300,到达时间噪声为均匀噪声,噪声水平为①10%;②15%;③20%;④25%;⑤30%;正确率对照试验结果如表2所示。

表2 不同噪声水平条件下两算法分选性能对照表

为了更加直观地体现出噪声水平对两种分选算法的影响程度,在3个信号源个数条件下,取噪声系数为因变量,变化范围从10%～40%,以1%为步进仿真对照两种分选算法的正确率。仿真结果如图8所示。

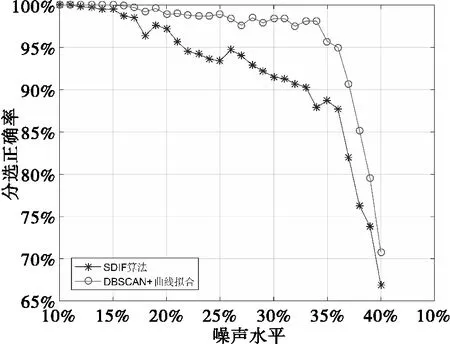
图8 三信号源条件下两种分选算法性能对照图

结论:由实验对照表和结果仿真图8可得,在相同3个待分选信号源条件下,当噪声水平大于15%时,DBSCAN聚类加曲线拟合的方法的分选正确率比SDIF算法高1.5%～14%不等,噪声水平在35%以内时,本文提出的方法分选正确率均能保持在95%以上,而SDIF若需保持相同分选正确率,噪声水平需不超过21%,证明相比之下,DBSCAN聚类加曲线拟合方法的抗噪性能更佳。

3)仿真对照实验3:

待分选信号源个数radarNum=2脉冲重复周期值分别为:PRI1=187、PRI2=230、到达时间噪声为均匀噪声,取噪声系数为因变量,变化范围从10%～40%,以1%为步进仿真对照两种分选算法的正确率。仿真结果如图9所示。

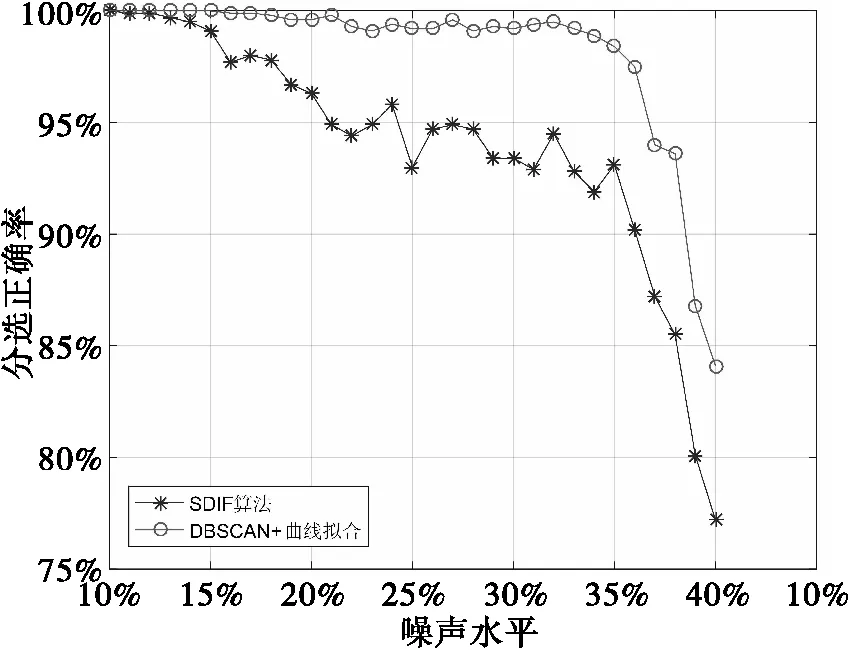
图9 两信号源条件下两种分选算法性能对照图

结论:由实验对照表和结果仿真图9可得,在相同2个待分选信号源条件下,当噪声水平大于15%时,DBSCAN聚类加曲线拟合的方法的分选正确率比SDIF算法高0.9%～13%不等,噪声水平在36%以内时,本文提出的方法分选正确率均能保持在95%以上,而SDIF若需保持相同分选正确率,噪声水平需不超过24%,证明相比之下,DBSCAN聚类加曲线拟合方法的抗噪性能更佳。

由仿真对照实验1可知,在4个信号源条件下,经典SDIF算法正确率有明显下滑,故此处不再对照该种条件下噪声水平变化对两种算法的影响。

4 结束语

针对传统SDIF算法在PRI分选处理中表现出明显的抗噪性能和抗谐波性能较差的问题,本文对基于密度的聚类算法进行了研究,提出了将DBSCAN聚类与曲线拟合相结合的PRI分选算法,首先通过DBSCAN聚类算法对噪声点的高敏感度,以及在分选处理中所表现出的良好抗谐波性能,提高正确识别PRI值的概率,从而为后续有效的序列抽取提供了基础。同时,由于信号到达时间序列所呈现出的线性关系,采用曲线拟合算法可以准确地从混叠脉冲序列中的提取出不同PRI值所对应的TOA序列。文中使用的DBSCAN算法可根据实际工程需求对邻域半径和核心样本点值等参数进行调整及优化。最后通过仿真验证了该方法的有效性,并和传统的SDIF算法在不同的分选效能方面进行对比,进一步说明了本文提出的PRI分选算法具有更高的正确识别概率。