加权空-频时间反转多目标成像

呼 斌 李 飞 王 伟 杜自成

(西安电子工程研究所 西安 710100)

0 引言

时间反转(TR)是一种可以对目标进行检测和定位的自适应传输技术,其广泛应用于声学[1]、超声波[2]和电磁领域[3-4]。TR技术将目标的回波信号进行时间反转操作后重新回传到原物理介质中,可以通过物理或者合成模式使得信号自动聚焦源的位置[5]。合成模式(计算TR)通过传播介质的格林函数来数值合成反向传播场的数据[6]。

两种主要的TR成像方法分别是TR算子分解算法[7](DORT)和TR多信号分类算法[8](TR-MUSIC)。DORT算法通过TR算子的信号子空间对应的特征向量构造成像函数,TR-MUSIC类的方法则是依靠噪声子空间对应的特征向量。这类算法都是基于对多站数据矩阵(MDM)的奇异值分解(SVD)。成像结果受MDM的秩(与散射点个数相关)的影响较大,尤其是当天线阵元数量较少时,成像结果对选取的噪声子空间向量的数量更为敏感。因此,对数据SVD后并根据矩阵的秩来适当地划分信号子空间和噪声子空间显得尤为重要。这两种方法都需要知道散射体的数量,这通常是通过文献[13-14]中的方法获得的。或者,TR成像函数可以通过统计测试[15]的方式来设计,因此可以不需要精确的目标数。类似的方法[16-17]在雷达相关应用中有着广泛应用。

本文中,提出了一种简单的近场成像方法,它对基于传统的计算TR成像方法中需要的目标确切数量不敏感。同时,研究了在成像中数据矩阵秩的确定(通过对MDM进行SVD获得)对成像结果的影响。本文提出的方法采用MDM的奇异值来加权TR成像函数,并确定了初始目标的数量。然后,提出了一种被改进的SF-TR,即W-SF-TR算法,获得稳定的 TR成像结果,并从理论分析了提高成像性能的原因。最后,给出了一些简单散射场景的数值算例验证了导出的结果。所有的结果都是基于自由空间背景假设,忽略了天线间的相互耦合、极化等影响。

本文的其余部分安排为:第二部分简要介绍了SF-MDM和SF-TR成像方法。提出了一种新的W-SF-TR成像算法。然后,第三部分给出了W-SF-TR算法的理论性能分析,并通过数值模拟对其进行了验证。最后,第四部分总结得出了结论。

符号表示:大写或小写的黑体字母表示向量或者矩阵;(·)H、(·)T, |·|以及Σ表示矩阵共轭转置、转置、绝对值和求和。

1 W-SF-TR成像算法

1.1 SF-TR算法

假设TR阵列包含N个天线阵元,TR阵列的第一个阵元发射所需的宽带信号,阵列记录下目标的回波数据,具体模型如图1所示。

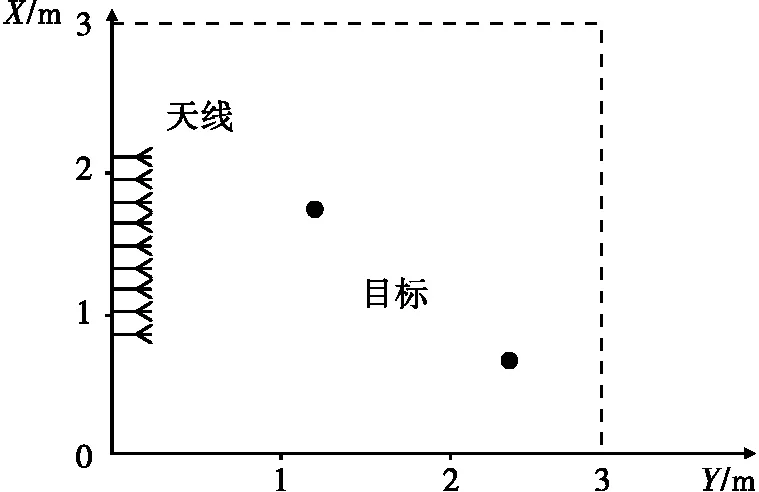
图1 多目标成像场景示意图

然后,将回波信号经过傅里叶变换转换到频域表示。设置采样频点个数为L。因此,空频多站数据矩阵(SF-MDM)可以表示为式(1)所示。

(1)

其中:ki(ωj), (i=1, 2, … ,N;j=1, 2, … ,L),表示第i个阵元接收到的回波信号在频域对应的第j个频点的均匀采样;ωL-ω1表示信号的带宽。

对K进行奇异值分解可得

K=UΛVH

(2)

其中:U是一个N×N的酉矩阵,其中的列向量为左奇异向量;V是一个L×L的酉矩阵,其中的列向量表示右奇异向量;Λ是一个N×L矩阵,其对角线元素表示相应的奇异值,这里U可以表示为

(3)

其中:ui表示第i个N×1的左奇异向量包含着空间(位置)信息[11]。其中,P-1个较大的奇异值对应的左奇异向量ui(i=1, 2, …,P-1)表示有P-1个较强的散射点,并构成了信号子空间;其余的左奇异向量ui(i=P, 2, …,N)对应U矩阵中较小的奇异值,并构成了噪声子空间。这里采用文献[12]中的方法,通过选择连续奇异值比值中的最大值确定P值,即通过公式(4)确定P值为

(4)

其中λn表示第n个奇异值。

SF-TR算法利用噪声子空间对目标进行成像,其成像公式可以表示为

(5)

其中,g(rs,ω)表示在探测区域的每个搜索位置rs处的背景格林函数向量,表示为

g(rs,ω)=[G(rs,r1,ω),G(rs,r2,ω),…,G(rs,rN,ω)]T

(6)

其中的每个元素G(rs,rN,ω)表示一个背景格林函数;rN表示第N个天线阵元的位置;ω表示角频率。

1.2 加权SF-TR算法(W-SF-TR)

在多目标成像场景中,P值的选取可能会影响成像的质量。因为P的大小决定了信号子空间或噪声子空间的大小,特别是当阵列中阵元数量较小时,P的不同值可能会严重影响了成像结果。因此,在所提出的W-SF-TR算法中,奇异值用于加权对应的左奇异向量,然后重新构造噪声子空间以减少噪声子空间大小对图像质量的影响。参考SF-TR成像公式(5),提出的W-SF-TR成像算法可以描述为

(7)

其中,λi(i=P,P+1, …,N)表示对应的奇异值。

2 W-SF-TR成像结果与讨论

通过矩量法(MOM)获得了自由空间中目标的SF-MDM。图1所示的即为多目标近场TR成像场景,构成一个3m×3m的探测区域。均匀间隔的线阵由9个偶极子天线构成,沿着x轴分布,间距为λc/2,其中λc为自由空间中心频率对应的波长。发射信号的中心频率fc=3GHz,带宽为400MHz,变换到频域的频率采样点数L=101。阵列的几何中心位于(0.1m,1.5m,0m)处。两个半径为5cm的理想导体金属球分别位于(1.8m,1.2m,0m)和(0.8m,2.4m,0m)处。

2.1 W-SF-TR算法成像稳健性分析

在本小节中,我们分析了W-SF-TR算法在成像性能中的优越性。

首先,我们计算得出了在不同的SNR条件下的奇异值分布,如图2所示。在理想情况下(无噪声的情况),奇异值的分布曲线显示前两个奇异值较大,第三、第四、第五个奇异值大于0,其余奇异值较小。然而,随着SNR的降低,与噪声子空间相对应的奇异值逐渐增大,因此很难直接通过奇异值的相对大小区分信号子空间和噪声子空间。

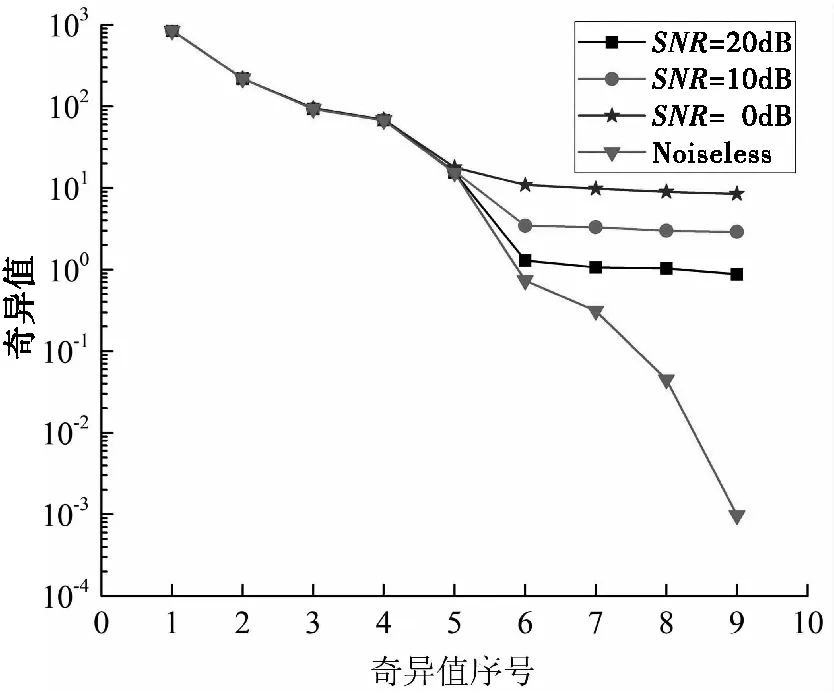
图2 不同信噪比条件下的奇异值分布对比

图3展示了不同SNR条件下连续奇异值的比值。根据式(4)和图3给出的结果可以看出,当SNR逐渐降低时,P在不同SNR条件下的对应值分别为9、6、6和2,对P值有显著影响。

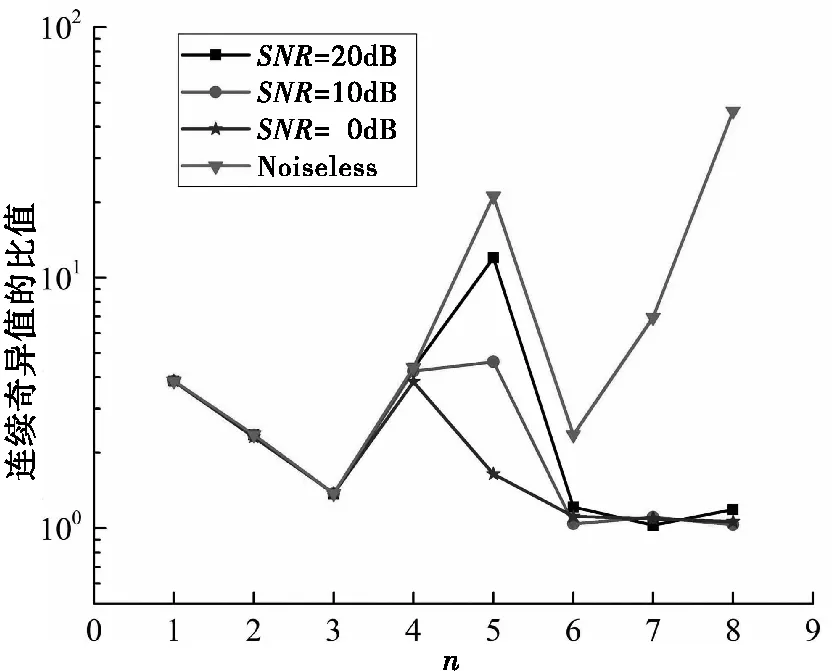
图3 不同信噪比条件下的连续奇异值比值

为了更直观地说明这个问题,当P的取值从3～8变化时,分别获得2个目标点的SF-TR成像结果。图4为SNR=0dB时P取不同值时的SF-TR成像结果(在图4和图5中,符号×代表了两个目标的实际位置)。当P=3和P=4时,目标位置的能量不能较好的聚焦,目标的位置难以确定。能量散布在如图4(a)所示的较大范围面积上。随着P的增加,对目标的聚焦效果逐渐变得更好。从图4的结果可以得出结论:噪声子空间的选择对多个目标的SF-TR成像结果影响非常大。P的值决定了如何区分信号子空间和噪声子空间,极大地影响了成像结果,并随着SNR的变化而变得不稳定。

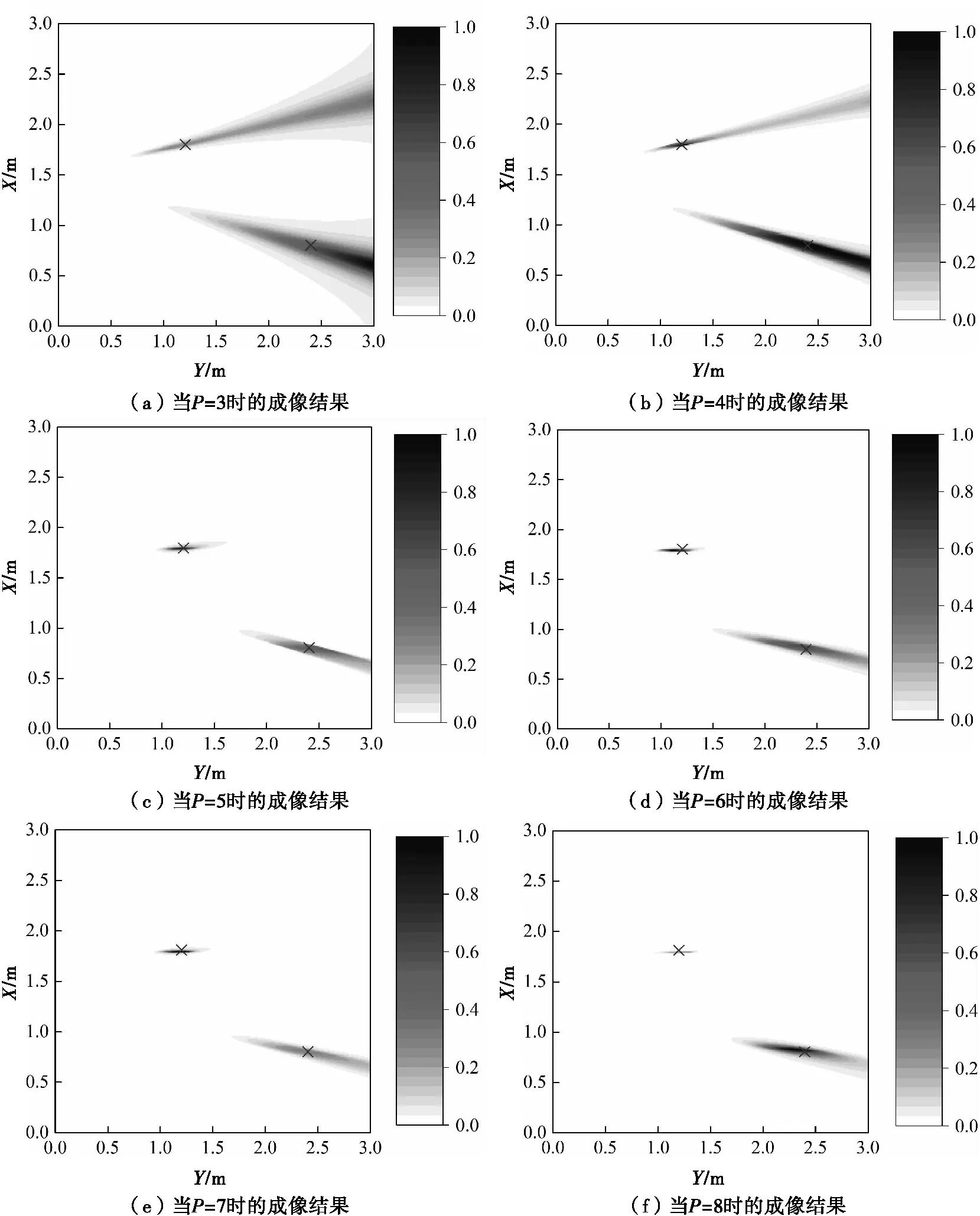
图4 多目标SF-TR成像结果(SNR=0dB)

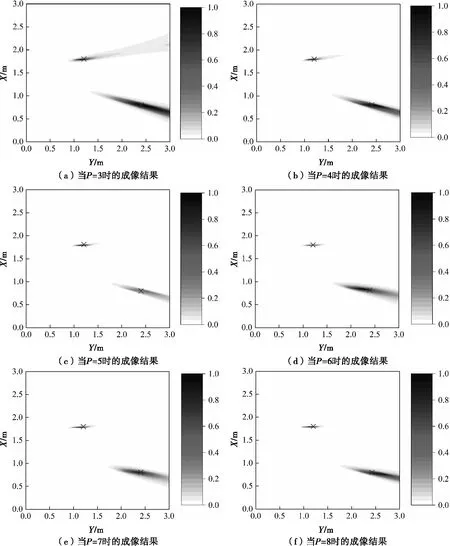
图5 多目标W-SF-TR成像结果(SNR=0dB)

其次,分析了W-SF-TR的成像稳定性和分辨率。假设我们已经划分的噪声子空间有N-P+1个向量构成,对应的奇异值符合式(8)形式。

λP≥λP+1≥…≥λQ≥λQ+1≥…≥λN≥0

(8)

假设噪声子空间中包含的Q-P-1个向量(Q≥P-1)本应属于信号子空间,却被误划分到噪声子空间。因此,式(7)的分母可以分为两部分,进一步表示为

(9)

这里应该注意到当Q=P-1时,式(9)右侧的第一项为0。

类似的,我们可以将式(5)重新表示为

(10)

根据式(8)、式(9)和式(10)可得

(11)

经过进一步运算,可得

(12)

式(12)中,第一项表示使用W-SF-TR算法后,噪声子空间部分与信号子空间部分(被错误分类到噪声子空间的部分)的比值;最后一项表示,在SF-TR中噪声子空间部分与信号子空间部分(被错误分类到噪声子空间的部分)的比值。这表明,奇异值向量的加权使在分母上的真实噪声子空间向量的比例增加,而一些被错误分类为噪声子空间的信号子空间向量的比例减小。因此,这些信号子空间向量被意外分配噪声子空间中造成的影响降低。

2.2 多目标W-SF-TR成像

在W-SF-TR成像过程中,式(7)被用于对两个目标进行成像。在图5(a)、图5(b)和图5(f)中,可以清楚地看到在使用W-SF-TR算法后,目标的成像结果优于图4中的相应未使用该算法时的结果。W-SF-TR算法对两个目标的成像位置与相应目标的实际位置相匹配。因此,随着P的变化,我们提出的成像方法将更多的能量集中在两个目标上,并且在低SNR情况下成像结果更加稳定。同时,在使用W-SF-TR后,P值的可选范围变得比SF-TR算法更大,成像结果对噪声子空间的选择变得不那么敏感。

2.3 W-SF-TR算法目标分辨率

为了进一步比较SF-TR算法和W-SF-TR算法的性能,图6和图7分别给出了两种算法的归一化横向和纵向分辨率对比。SF-TR算法的横向和纵向分辨率随着P值的变化产生明显变化。通过将W-SF-TR算法应用到SF-MDM中,当噪声子空间如图6所示时,我们实现了对多目标稳定的横向和纵向分辨。从图6(a)可以看出,当选择了不同的P值时,能量集中在SF-TR算法的两个目标上发生了显著的变化。当P的值为3和4时,横向分辨率非常差,能量很难集中在两个目标上。当P的值在3～8范围内变化时,在X=0.8m和X=1.8m的两个目标位置处的聚焦能量差分别达到28.9dB和24.5dB。

图6 两目标TR成像的横向分辨结果对比(SNR=0dB)

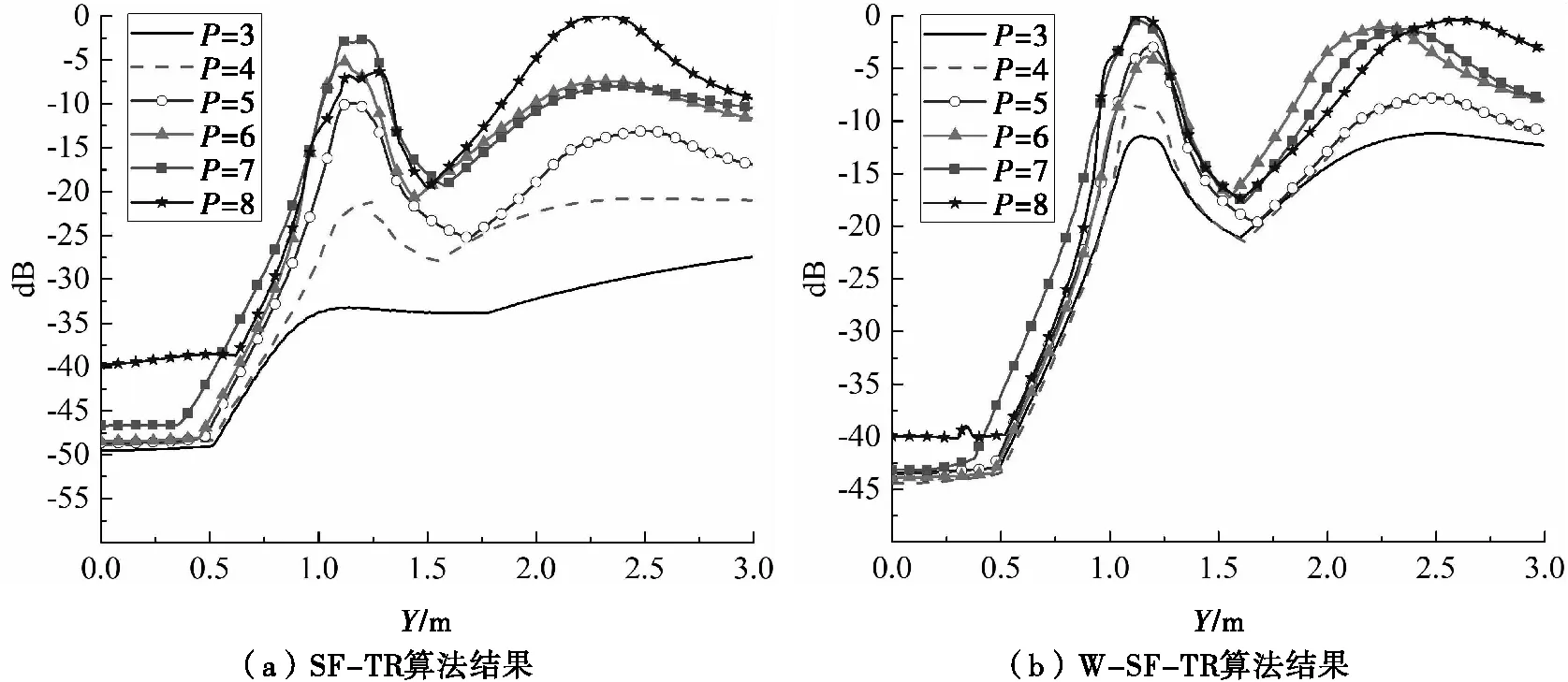
图7 两目标TR成像的距离向分辨结果对比(SNR=0dB)

图6和图7的对比结果表明,SF-TR成像算法对P值的选取非常敏感,即噪声子空间的大小。在使用本文提出的W-SF-TR算法后,如图6(b)所示,在X=0.8m和X=1.8 m处的两个目标的聚焦能量差值分别显著降低到10.0dB和5.3dB。类似地,图7中的对比结果也表明,W-SF-TR算法的距离分辨效果也优于SF-TR算法。当P的值变化时,在Y=1.2 m和Y=2.4m处的两个目标的聚焦能量波动范围分别达到了30.6dB和29.5dB。通过采用W-SF-TR算法,其波动范围减少到11.0dB和10.1dB。

总的来说,给出的成像结果表明W-SF-TR算法可以在横向和距离向实现目标的高分辨成像,并在低信噪比、P值变化的情况下获得稳定的成像结果。因此可以从W-SF-TR成像结果中得出结论:该方法可以自适应的调整TR成像的负面影响,并在P变化时进行稳定成像。

3 结束语

本文提出了多目标近场W-SF-TR成像算法,该算法克服了传统SF-TR成像算法在选择不同P值时造成的潜在不稳定成像结果。新算法通过引入噪声子空间向量加权因子(对应的奇异值),使得确定噪声子空间大小的P值的选择范围扩展到一个较大的动态范围。当P在大范围内波动选取时,W-SF-TR算法仍然可以取得优异的成像结果,这也有利于移动目标成像。在低SNR的情况下,通过两个近场PEC目标验证了W-SF-TR算法的有效性。结果显示,在对多目标进行TR成像时,提出的W-SF-TR算法表现优异,显示出了稳定的成像效果。此外,W-SF-TR算法对多目标的成像分辨稳健能力也优于SF-TR算法。