一道全国高中联赛题的解法赏析及溯源

安徽省合肥市肥东县城关中学 (231600) 王东海

1 真题呈现

(2022年全国数学联赛第10题) 给定正实数m(m≥3).设正项等差数列{an}与正项等比数列{bn}满足:{an}的首项等于{bn}的公比,{bn}的首项等于{an}的公差,且am=bm,求am的最小值,并确定当am取最小值时a1与b1的比值.

分析：观察此题,应首先用尽量少的变量表示am,得到am的函数式,然后考虑使用导数法或均值不等式来求解am最值.

2 解法探究

探求思路一设出{an}和{bn}的公差和公比,用这两个变量去表示am.

探求思路2 使用上述解法在求导数时较为复杂,运算量较大,若换元后求导可简化运算.

探求思路3 除了使用导数法求最小值外,我们还可使用多元均值不等式加以求解.

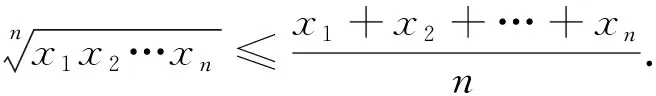
解析3:设{an}的公差是d,d>0,{bn}的公比为q,am=q+(m-1)d,bm=dqm-1,

探求思路四解析3使用了换元法,将所求设为λ往往不易想到,也可直接使用均值不等式.

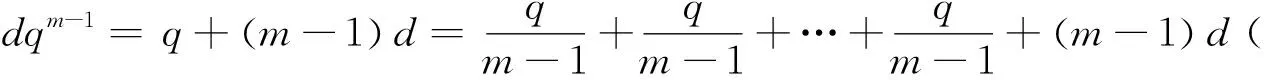
探求思路六从另一个角度也可直接使用均值不等式,对培养学生的发散思维大有裨益.

解析5 设{an}的公差是d,d>0,{bn}的公比为q,am=q+(m-1)d,bm=dqm-1,

探求思路六解法5对函数采取分子分母同除以分子的技巧,我们还可考虑下面的处理策略.

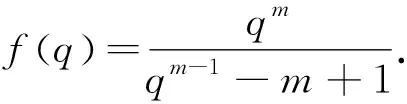
3 追本溯源

题1 (2016年高考Ⅰ卷16题)函数y=2sinx+sin2x的最小值为.

解析：

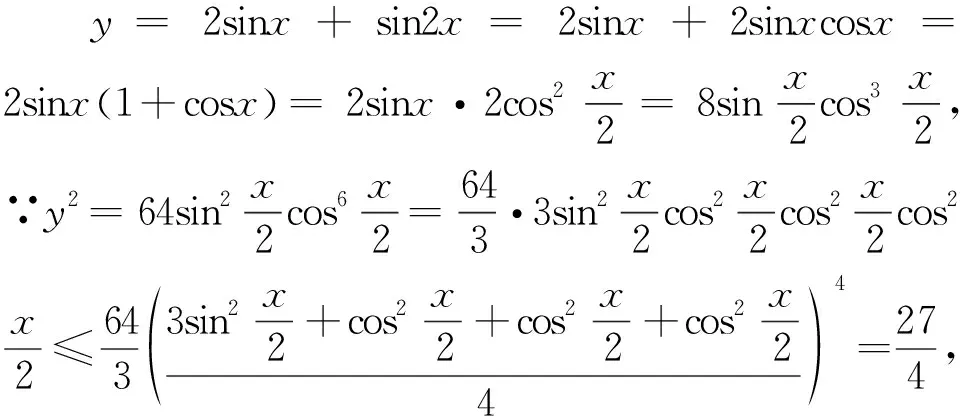
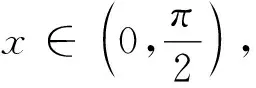
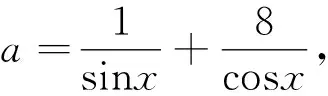
4 结语

本题题目新颖,将数列与导数、均值不等式相结合,在知识的交汇处命题.处理时切入点较多,本文呈现了几种常见的解法,事实上还有其它解法,囿于篇幅,不一一介绍,希望能抛转引玉,同广大读者共同探讨解法.