例析解析几何中的垂直关系
2023-07-15 06:26:14安徽省砀山中学235300盖传敏
中学数学研究(江西) 2023年7期
安徽省砀山中学 (235300) 盖传敏
垂直关系是解析几何中的一种特殊位置关系,对于垂直关系我们往往需要进行合理有效地转化,然后进行求解,下面结合实例谈谈垂直关系转化的若干途径.
1 斜率与垂直关系的转化
例1 若直线l1:x-2y+5=0与直线l2:2x+my-6=0互相垂直,则实数m=________.
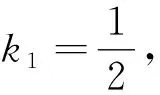
评注:在运用斜率判定两直线垂直时,首先要对直线斜率的存在性进行讨论,若两直线的斜率存在且不为0,可将两直线垂直可转化为两直线的斜率乘积等于-1进行求解.
2 向量与垂直关系的转化
例2 已知点M(-1,1)和抛物线C:y2=4x,过C的焦点且斜率为k的直线与C交于A,B两点.若∠AMB=90°,则k=________.
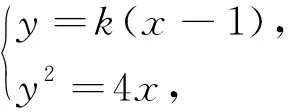
评注:将直线之间的垂直关系转化为向量之间的垂直关系,再转化为向量的数量积为0进行求解.
3 勾股定理与垂直关系的转化
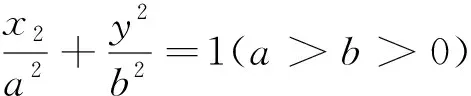
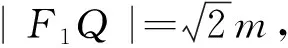
评注:通过垂直关系构造适当的直角三角形,再利用勾股定理找出边角之间的关系进行求解.
4 圆与垂直关系的转化


评注:由平面几何知识可知圆中的直径所对的圆周角是90°,因此通过垂直关系可构造适当的圆,然后利用圆的性质进行求解.
5 隐性的垂直关系
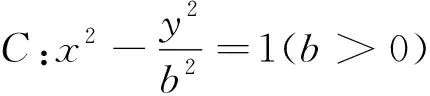
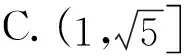
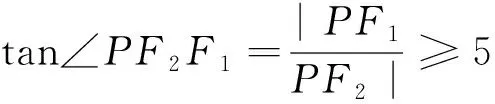
评注:如果题设条件没有直接给出垂直关系,这时需要借助几何图形性质挖掘垂直关系,然后进行合理转化再进行求解.
猜你喜欢
数理化解题研究(2022年22期)2022-08-30 06:37:58
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26 14:04:56
中学生数理化(高中版.高考数学)(2021年9期)2021-11-05 08:17:54
河北理科教学研究(2021年1期)2021-06-07 07:49:14
中学生数理化·中考版(2020年11期)2020-12-14 07:00:24
中学数学杂志(初中版)(2019年4期)2019-09-18 15:15:11
新高考·高二数学(2018年1期)2018-11-20 02:15:42
广东教育·高中(2018年12期)2018-02-13 01:26:40
中学化学(2017年6期)2017-10-16 17:22:41
初中生世界·九年级(2017年9期)2017-10-13 09:39:50

