圆锥曲线中非对称韦达式的处理策略*
——一道考查数学运算素养的高三试题分析
2023-07-15 06:26福建省泉州第一中学362000张国川任晓红
中学数学研究(江西) 2023年7期
福建省泉州第一中学 (362000) 张国川 任晓红
解析几何试题中,以斜率关系为考查背景的试题在各地模拟试题中经常出现,其本质常与圆锥曲线的第三定义有关,深层次的理论依据则是高等几何中的极点极线问题.利用代数方法解决几何问题的核心是将几何基本量代数化,如将斜率用两点坐标表示,再根据题目将所要求解的斜率表达式整合成对称韦达式,并将韦达定理整体代入求解即可.然而在一些模拟试题中却出现了一些非对称韦达式,比较简单的通常是将韦达定理中的两个式子相除,得到两根和与积的倍数关系,代入化简即可.可是有些试题如是操作却不可行,本文结合一道高三试题的运算处理谈谈非对称韦达式的处理策略,以此抛砖引玉.

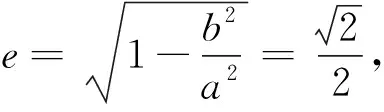

本题的难点在于如何处理非对称式5x1+2x2=2,化归成同系数韦达定理才能整体代入,实现运算简化的目的.下面给出四种常见的非对称韦达式的运算处理策略:
策略1同系数配凑法
策略2方程求根法

策略3待定系数法
由策略1的③式,知-9x1x2=[5(x1+x2)-2][2(x1+x2)-2](*)
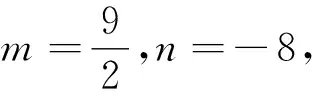
策略4倒数构造法
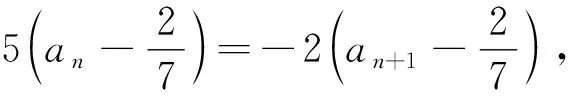
结语非对称韦达式是圆锥曲线中一类比较特殊的代数结构,对学生处理代数式子的要求比较高,本质上是考查学生如何将非对称式子转化成为称式子,和数列中将非特殊数列化成特殊的等差或等比数列有异曲同工之妙,命题者的意图旨在通过试题考查学生数学运算的核心素养,有利于培养学生熟练的式子变形能力,符合解析几何考查代数运算求解能力的基本要求.
猜你喜欢
小猕猴智力画刊(2021年11期)2021-11-28
数学小灵通·3-4年级(2021年5期)2021-07-16
中学数学杂志(高中版)(2021年2期)2021-06-02
中学数学杂志(高中版)(2021年3期)2021-05-10
河北理科教学研究(2020年1期)2020-07-24
数学年刊A辑(中文版)(2018年2期)2019-01-08
中等数学(2017年10期)2017-02-06
数学小灵通·3-4年级(2016年4期)2016-11-25
数学理论与应用(2016年4期)2016-05-17
电测与仪表(2015年4期)2015-04-12

