巧用均值不等式证明数学奥林匹克不等式题
2023-07-15 06:26南昌大学附属中学330047
中学数学研究(江西) 2023年7期
南昌大学附属中学 (330047) 周 辉
均值不等式是一个应用非常广泛的不等式,在证明不等式问题时,为了创设使用均值不等式的条件,常常需要对题中的式子作适当的变形,而变形的出发点又常常是在兼顾所给条件的基础上注意不等式的取等条件.
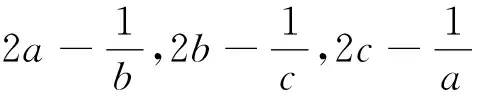
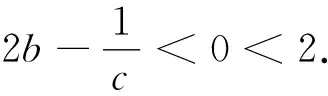
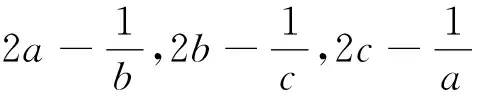
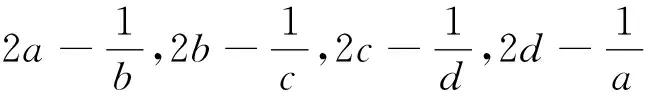
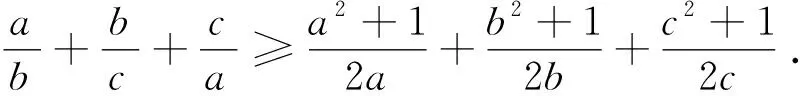
证明：由均值不等式可得
以上三式相加得
推而广之,我们有(证明留给读者):
已知a,b,c是满足abc=1的正数,k是正整数,求证:
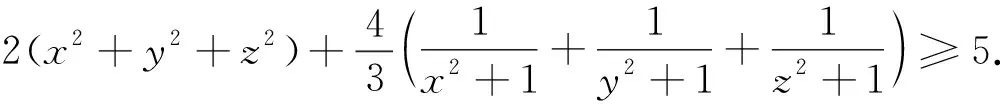
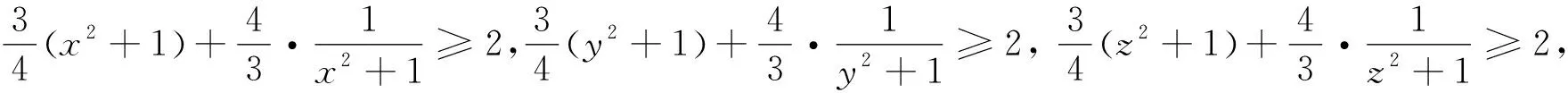
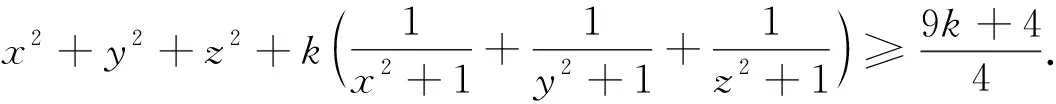
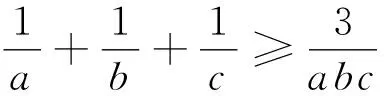
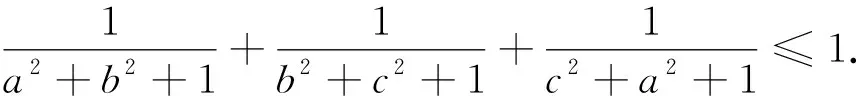
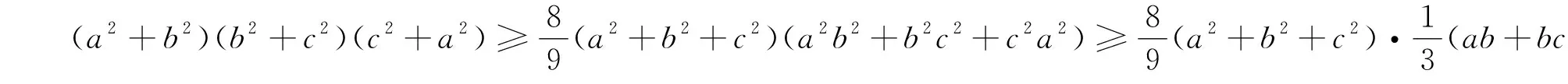
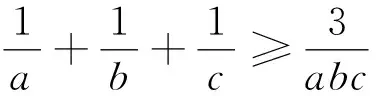
例5 (2022年印度数学奥林匹克试题) 已知x,y是满足xy=1的实数,求证:
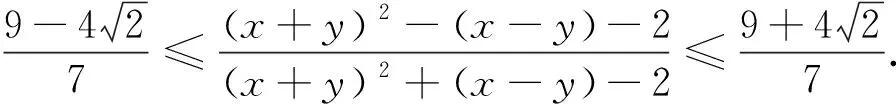
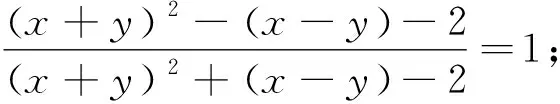
当然利用xy=1可以直接转化为一元不等式来处理,但对本题而言,远没有先换元后转化这样简单快捷. 文末,我们编拟一道有趣的类似题留给读者完成证明 :
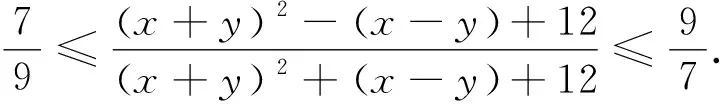
猜你喜欢
南昌大学学报(医学版)(2022年3期)2022-07-20
南昌大学学报(医学版)(2022年2期)2022-05-30
江苏教育(2021年54期)2021-08-31
中小学校长(2021年7期)2021-08-21
南昌大学学报(医学版)(2021年3期)2021-07-21
南昌大学学报(医学版)(2020年3期)2020-08-17
小学生作文(低年级适用)(2019年10期)2019-10-28
作文周刊·小学五年级版(2019年16期)2019-06-12
作文小学高年级(2019年3期)2019-01-10
中学生英语·外语教学与研究(2017年3期)2017-05-19
