一道高考函数试题的解题方略
2023-07-17 01:40江西省高安中学330800朱细秀
中学数学研究(江西) 2023年7期
江西省高安中学 (330800) 朱细秀
2020年江苏卷命制的函数综合题考查内容丰富,试题共设置了三小问,三小问中的函数各异,设问涵盖了求函数解析式,参变量的取值范围以及不等式的证明等众多内容, 要求考生熟练地掌握函数的图像与性质,运用导数这一研究函数性质的利器,以及数形结合、分类讨论等众多数学思想与方法才能顺利地完成试题的求解,本文试对此作出评析.
试题已知关于x的函数y=f(x),y=g(x)与h(x)=kx+b(k,b∈R)在区间D上恒有f(x)≥h(x)≥g(x).
(1)若f(x)=x2+2x,g(x)=-x2+2x,D=(-∞,+∞),求h(x)的表达式;
(2)若f(x)=x2-x+1,g(x)=klnx,h(x)=kx-k,D=(0,+∞),求k的取值范围;

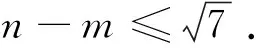
析解:(1)由f(x)≥h(x)≥g(x),说明等号也有成立的因素,故由x2+2x=-x2+2x,得x=0,则其中间函数h(x)满足h(0)=0,所以b=0,又f′(x)=2x+2,g′(x)=-2x+2,所以g′(0)=f′(0)=2,所以h(x)=2x.由图1可以看出,当h(x)=2x时,满足要求.(实际上直线h(x)=2x在x=0处与两函数f(x)=x2+2x,g(x)=-x2+2x图像都相切,在区间(-∞,0)∪(0,+∞)上,f(x)=x2+2x图像恒在h(x)=2x图像上方,g(x)=-x2+2x图像恒在h(x)=2x图像下方.)

图1


猜你喜欢
中学生数理化·七年级数学人教版(2022年9期)2022-10-24
初中生学习指导·中考版(2022年4期)2022-05-12
有色金属(矿山部分)(2021年4期)2021-08-30
中等数学(2020年1期)2020-08-24
新世纪智能(教师)(2019年1期)2019-09-11
数理化解题研究(2019年1期)2019-02-15
中学历史教学(2017年11期)2017-12-20
中学历史教学(2016年11期)2016-03-01
中学数学杂志(2015年9期)2015-01-01
应用数学与计算数学学报(2014年2期)2014-09-26

