轨道平面外直线形绳系编队系统运动状态解析关系

汤毓宁, 余本嵩

南京航空航天大学航空航天结构力学及控制国家重点实验室, 南京 210016

0 引 言

近年来,随着理论水平和实验技术不断发展,人类对太空实践的需求愈加迫切.绳系卫星系统以其在深空探测、卫星通信、立体成像、碎片捕获等领域的独特优势进入了人们的视野,而绳系卫星编队作为其重要衍生同样引起了国内外学者的广泛关注[1-10].

绳系卫星编队是指多个卫星或航天器通过系绳连接,卫星之间保持相对静止并以特定的编队构型在轨飞行.学界已提出越来越多的新型编队构型.SU等[11]研究卫星速度未知情况下的三角形绳系编队系统的控制问题,讨论开环系统平衡点附近的稳定性,并设计一类非线性状态观测器对系统进行相应的控制.QI等[12]提出一类双金字塔形编队构型,将卫星通电使其因库仑力相互排斥以得到编队稳定的效果.HUANG等[13]研究轮辐绳系编队系统并基于合理假设提出对应解析模型对自旋过程中的轮辐绳系编队系统的动力学加以描述,提出两种编队控制策略并通过数值模拟加以验证.LUO等[14]通过柔性多体动力学方法研究三体绳系编队系统旋转动力学,提出一类两颗子卫星通过柔性系绳并沿阿基米德螺线轨迹移动的动力学模型,最后通过数值模拟探究其动力学响应及系统参数对系统释放及回收过程的影响.JUNG等[15]研究三体绳系卫星系统在释放和回收过程中的非线性动力学行为,建立具有6个自由度的哑铃模型,在不同初始状态和不同参数下,对其姿态动力学进行分析和比较.

近年来,关于绳系编队系统稳定性的研究取得了一定进展.KUMAR等[16]研究三角形绳系卫星编队构型并通过数值仿真得出了系统参数的设计阈值,得出该构型编队自旋速度必须达到临界值才可保证系统在轨道平面内保持自旋稳定状态,还分析系绳释放回收对系统动力学响应的影响.AVANZINI等[17]研究参考轨道偏心率与多体绳系卫星编队系统动力学特性的相关性,通过数值模拟研究了系统稳定性,并评估偏心率对系绳伸长量、编队构型等方面的影响.基于Hill近似,CAI等[18]提出一种新的关于系统姿态及轨道运动的动力学方程,研究释放和回收阶段平动点附近绳系卫星系统旋转三角形构型的动态稳定性,为解决任意平面下旋转三角形绳系卫星编队问题打下基础.ALARY等[19]研究一类金字塔编队构型的绳系编队系统的动力学,假定通过低推力火箭助推器维持各卫星位置保持构型,提出一种控制策略稳定其自旋状态,并通过数值模拟验证系统的可行性.YU等[20]研究在近地轨道上运动的三体绳系卫星编队系统的旋转稳定性,通过Floquet理论分析了系统周期运动的稳定性,并构建了等效的地面试验验证稳定性分析的有效性,结果表明,当系统旋转角速率超过临界值可以保持稳定的周期运动.TRUSHLYAKOV等[21]研究用于清除太空碎片的自旋绳系卫星系统的纵向振荡,提出一种新型算法,以将系绳的最大变形量最小化.

值得注意的是,大多数已发表的著作只涉及常规轨道平面绳系卫星系统的动力学和控制问题,而很少关注非轨道平面上的系统动力学问题.同时,学者们仅从数值角度对自旋角速度阈值和自旋稳定条件进行研究,鲜有通过解析关系进行求解.本文研究任何轨道平面直线形绳系卫星系统的动态特征,推导系统动力学解析关系式并分析初始状态对动力学行为的具体影响,最后提出一个三维动力学参数域加以展示,并通过数值仿真对解析关系式和结论加以验证.

1 系统动力学建模

本节建立了一类在正交控制力约束下,轨道平面外三星直线排列的绳系编队系统动力学模型.

如图1(a)所示,研究运行于近地圆周轨道的直线型绳系卫星编队.该系统由一颗质量为mM的母卫星M、两颗质量为mS的子卫星S1和S2及两根具有弹性的系绳组成.由于卫星尺寸远小于系绳长度,因此将3颗卫星简化为质点.此外,由于系绳质量远小于卫星质量,故不妨将空间系绳简化为无质量弹性系绳.系绳的刚度和无应变长度分别为EA和L0.假设系统质心以恒定轨道角速度Ω绕地运行,轨道半径为rO,P和ν分别为近地点和真近点角,同时在系统运动平面上定义面内俯仰角θ.

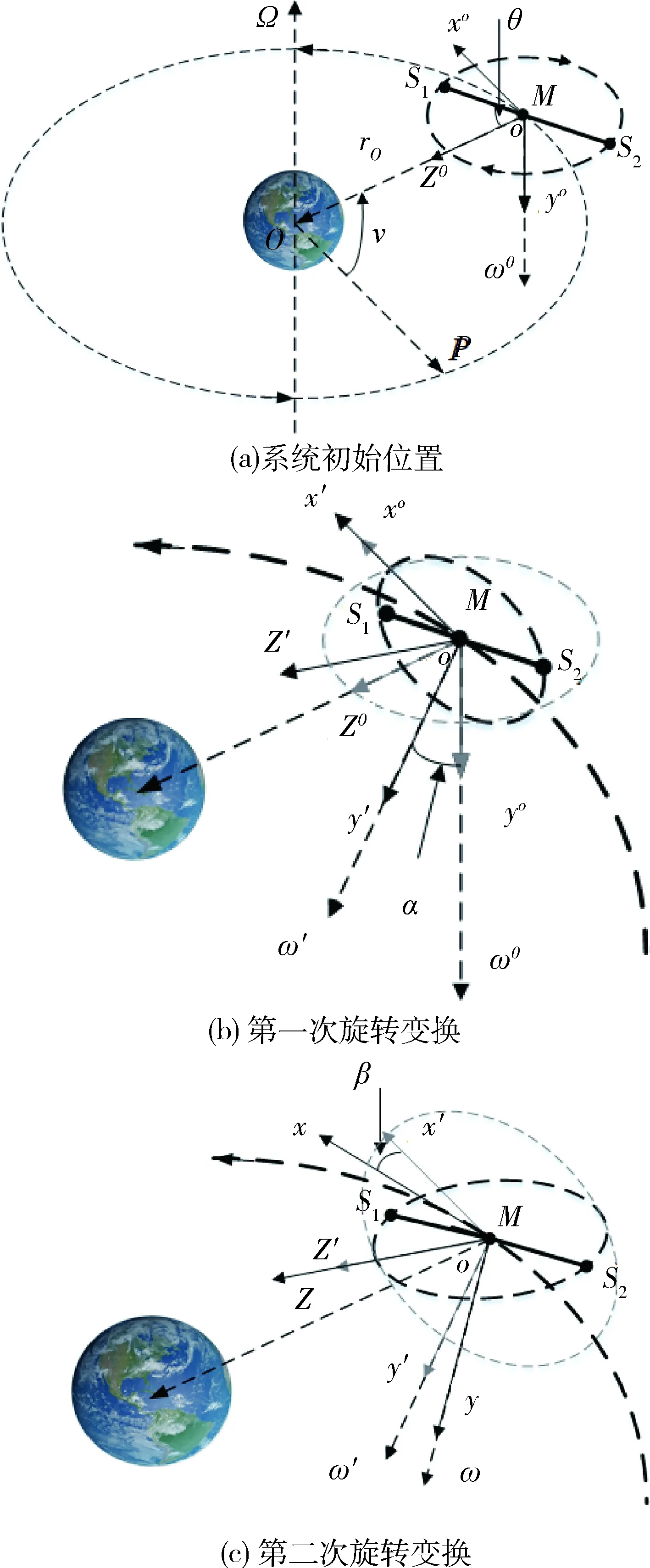
图1 轨道平面外直形型绳系编队系统Fig.1 A linear tethered system in nontypical planes

为更好地描述系统动力学建模过程,在此引入3组非惯性坐标系,第一组轨道坐标系o-xoyozo,如图1(a)所示,其中系统质心为原点o且位于圆轨道上,xo轴与轨道相切,yo轴正交于轨道平面,zo轴满足右手法则.系统自旋轴垂直于轨道平面,即ωo平行于Ω.

将第一组坐标系o-xoyozo绕xo轴正方向旋转α后得到第二组轨道坐标系o-x′y′z′,如图1(b),显然yo轴与y′轴(zo轴和z′轴)的夹角亦为α.

再将第二组坐标系o-x′y′z′绕z′轴正方向旋转β后得到第三组轨道坐标系o-xyz,如图1(c)所示,显然x′轴与x轴(y′轴和y轴)的夹角同样为β,以平面o-xz建立系统运动平面,自此实现了轨道平面外绳系卫星编队系统的构建.需注意,系统必须施加面外控制力才能保持面内运动.

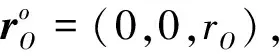
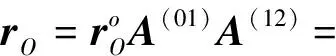
(1)

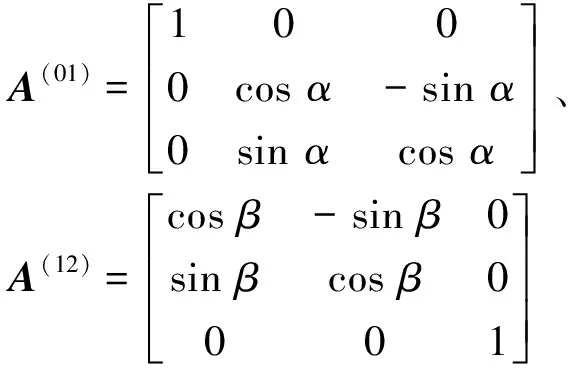
通过牛顿第二定律,得到在非惯性系o-xyz下母卫星M和子卫星S1(S2)的动力学方程分别为

(2)

和

(3)

式中,rM=[xMyMzM]和rS1(S2)=[xS1(S2)yS1(S2)zS1(S2)]分别为母卫星M和子卫星S1(S2)的位置矢量,t为轨道运行时间.

重力加速度的表达式为

(4)

式中,μE=3.988 5×1014为地心引力参数.

母卫星M和子卫星S1(S2)之间由于系绳牵引受到的系绳张力为

(5)

式中,符号函数δ定义如下:

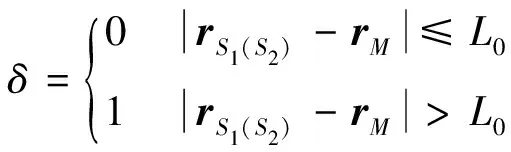
(6)

母卫星M和子卫星S1(S2)的牵连惯性力和科氏惯性力写成如下形式:

FM[(S1(S2)],Ie=-mΩ×[Ω×(rM[(S1(S2)]-rO)]

(7)

和

FM[(S1(S2)],IC=-2mΩ×vM[(S1(S2)]

(8)

式中,Ω=[0 -Ω0]为轨道角速度,vM[(S1(S2)]=drM[(S1(S2)]/dt为卫星的相对速度.

面外控制力表示如下:

FM[(S1(S2)],c=[FM[(S1(S2)],cxFM[(S1(S2)],cyFM[(S1(S2)],cz]

(9)

式中,FM[(S1(S2)],cx、FM[(S1(S2)],cy和FM[(S1(S2)],cz分别为FM[(S1(S2)],c沿x、y和z轴的分力.

所建立的动力学模型可以描述任意轨道平面内的直线形绳系卫星系统的动力学行为,符合执行指定方位光学成像等复杂太空任务的实际情况.

2 运动形式与系统状态的关系

本节基于所建模型的动力学方程,推导出子卫星角速度和系绳张力大小两者与子卫星面内俯仰角之间的解析关系,以进一步揭示运动形式与系统状态的关系.

由式(8)可知,科氏惯性力的方向与系统运动方向有关,而运动方向不同将导致系统动力学表现产生巨大差异.因此,本节将分别讨论子卫星初始时刻逆时针旋转(ω0<0)和顺时针旋转(ω0>0)两种情况,通过推导得出系统运动解析式以探究初始面内俯仰角θ0和初始角速度ω0与系统动力学响应的关系.

在此规定俯仰角θ=0对应的方向始终为z轴正半轴所指方向,假设母卫星始终位于非惯性坐标系o-xyz的原点o,系绳长度变化忽略不计.取子星S1为研究对象,对其受力情况进行分析,子星S1从初始面内俯仰角位置θ0顺时针旋转(ω0>0),运行至当前面内俯仰角位置θ时受力图如图2所示,逆时针旋转(ω0<0)时FS1,ΙC方向与图2所示FS1,ΙC方向相反.

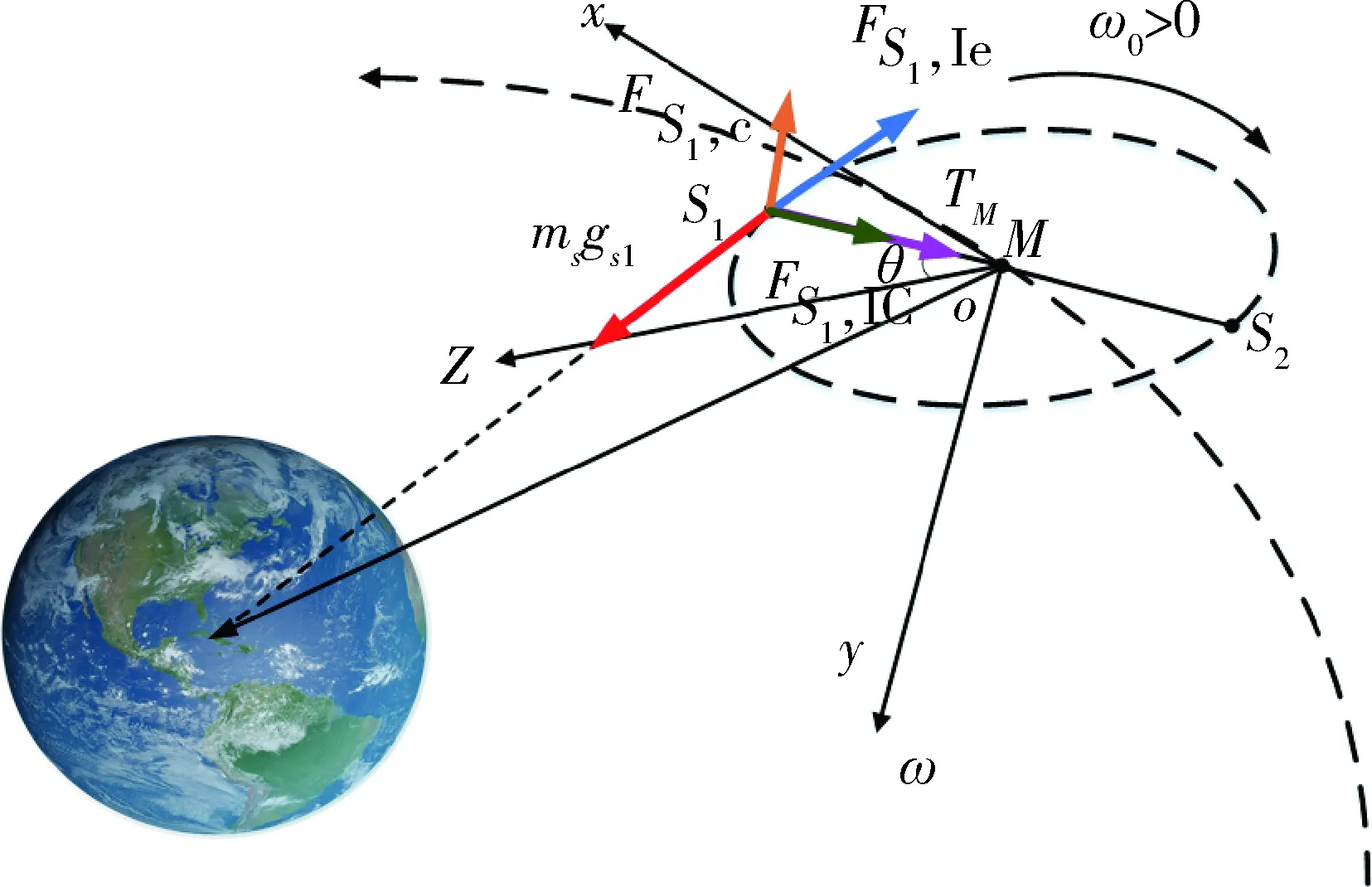
图2 子星S1受力分析图Fig.2 Force of sub-satellite S1

将式(3)向oS1方向l=[sinθ0 cosθ]T投影得

(10)

式中,θ为子星当前俯仰角,ω为子星当前角速度,L为系绳长度,T为系绳张力大小.

根据能量守恒定理,子星运动阶段满足如下关系:

(11)

式中,WIe为牵连惯性力所做的功,Ep和Ep,0分别为子星当前位置和初始位置的势能.

当子星运动至俯仰角θ=φ对应的位置时,对应位置沿轨道面的切线方向为n=[cosφ0 -sinφ]T,将力FS1,Ie向切向方向n进行投影,得到子星沿轨道面的切向分力

(12)

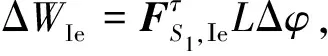
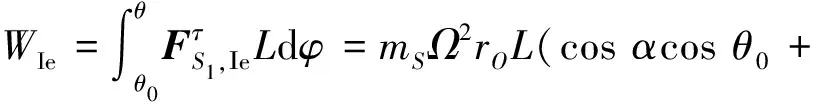
(13)

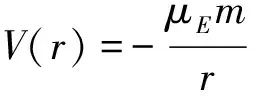
(14)

和

(15)

将式(13)～(15)代入式(11)得

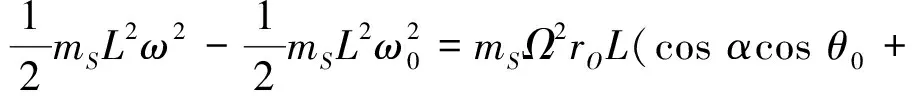
(16)

通过变形即可得到子星在系绳不松驰状态下的角速度与面内俯仰角的关系为

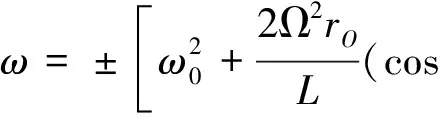
(17)

当子星逆时针旋转时ω取负号,顺时针旋转时ω取正号.

同时,将式(17)代入式(10)可以得到在系绳不松驰状态下系绳张力大小与面内俯仰角的关系.

通过该解析关系分析可进一步分析系统受力变化情况从而进一步揭示运动形式与系统状态的关系.显然,该系统运动解析关系对于常规轨道系统同样适用.

3 动力学分析

下面将通过系统运动解析关系式探究子星运动过程中角速度变化及受力变化情况,并分析初始状态对系统动力学行为的具体影响.

通过式(17)可得

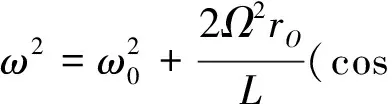
(18)

将其对θ进行求导得

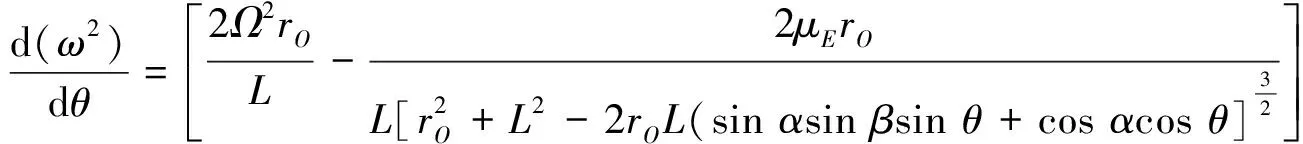
(19)

(20)

实际情况下rO远大于L时,可以求得

(21)

所以arctan(tanαsinβ)+kπ是|ω|的极大值点,arctan(tanαsinβ)+(k+0.5)π是|ω|的极小值点,其中k为任意整数.

将整个系统向xoz平面投影,发现面内俯仰角θ=arctan(tanαsinβ)所对应的方向与地球与母星的连线方向在平面上的投影一致,为了描述方便,记θΔ=arctan(tanαsinβ),所对应的位置为Δ,如图3所示.

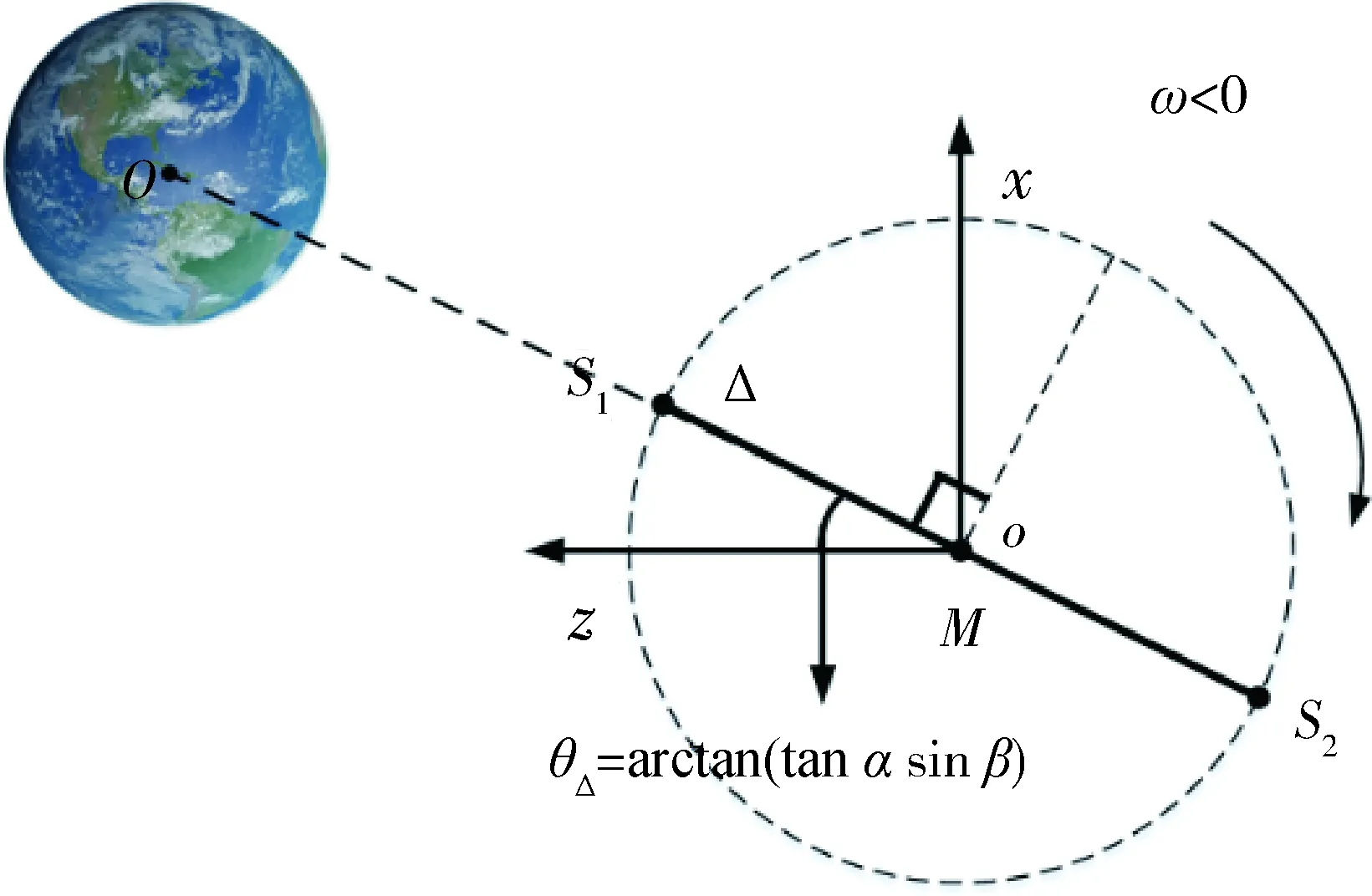
图3 临界位置Fig.3 Critical position

根据初始俯仰角和初始角速度的取值变化,系统动力学行为将分为3种情况:摆状振荡运动、自旋运动和不规则运动.首先讨论子星初始时刻逆时针旋转(ω0<0),根据式(10)和式(17)的关系式计算得出了摆状振荡运动和自旋运动对应的子星角速度和系绳张力随俯仰角变化关系图如图4所示.

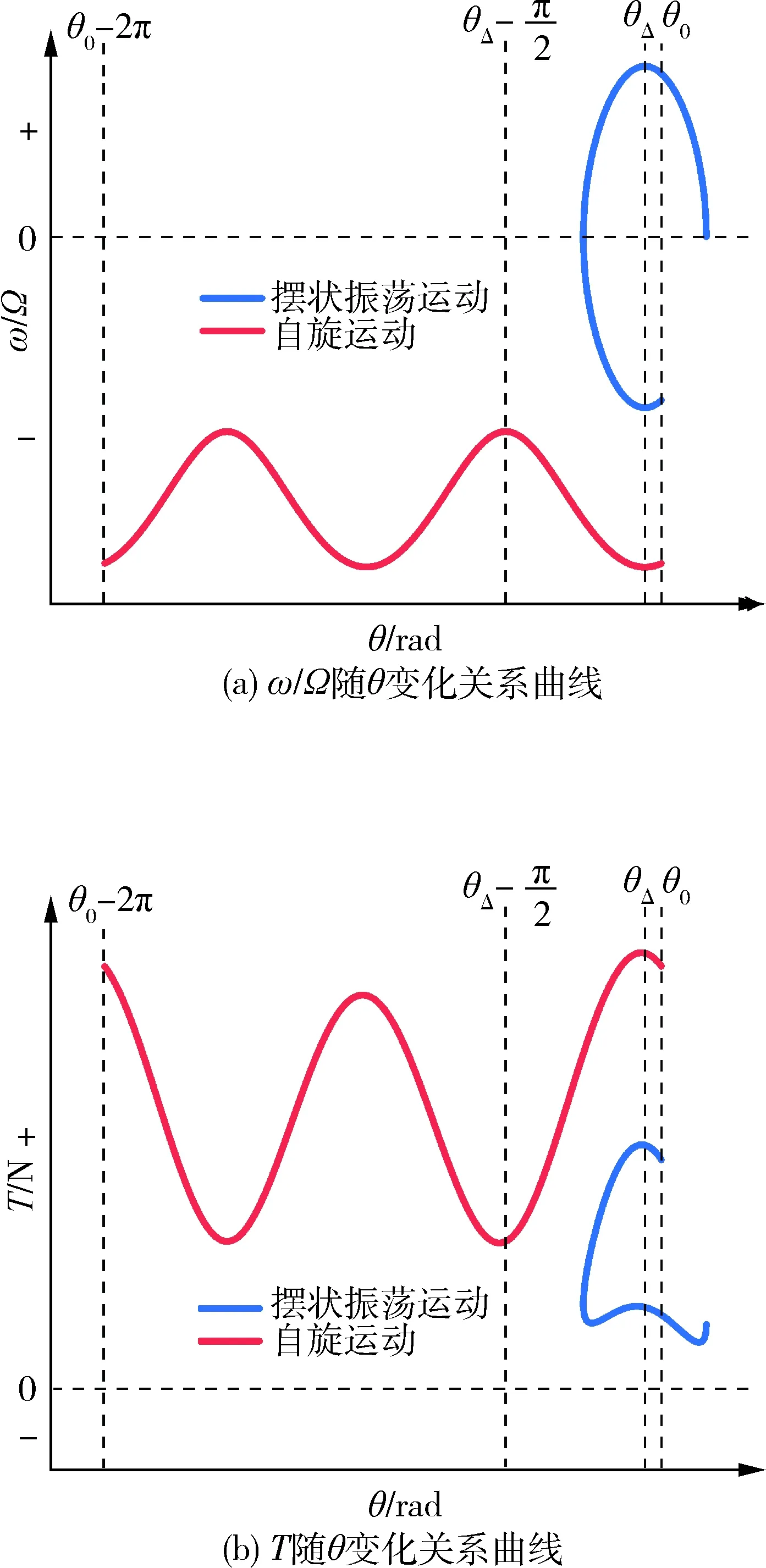
图4 初始角速度ω0<0状态下角速度和系绳张力随俯仰角关系变化曲线Fig.4 Angular velocity ω/Ω and tether force T versus pitch angle θ in initial angular velocity ω0<0

(1)摆状振荡运动(蓝色线条)

由于角速度大小|ω|在θ∈(θΔ-π/2,θΔ)单调递增,所以当子星初始角速度大小|ω0|和初始俯仰角大小|θ0|小于一定值时,子星角速度大小|ω|将在达到θ=θΔ-π/2对应的极小值位置点之前减为零,随后将顺时针反向运动.令式(17)中ω=0 可以得到卫星可到达最远位置所对应的俯仰角θmax.根据能量守恒,子星将在最远位置及其关于oΔ连线的对称位置往复运动,且运动过程中系绳张力始终存在,故系统不发生系绳松弛现象.

(2)自旋运动(红色线条)

当卫星初始角速度大小|ω0|达到自旋阈值时,可以保证卫星运动通过θ=θΔ-π/2对应的极小值位置点时角速度大小|ω|仍大于零,运动过程中系绳张力始终存在,不发生系绳松弛现象.之后将继续运动,并再次回到初始位置,完成圆周运动,且运动具有周期性.将θ=θΔ-π/2代入式(17)得到角速度ω(ω<0),将ω和θ=θΔ-π/2代入式(10),令T≥0,即可得到初始时刻逆时针旋转(ω0<0)情况下的自旋阈值.

(3)不规则运动

子星在到达θ=θΔ-π/2对应的极大值位置点之前系绳张力持续减少,根据式(10)可知,当子星初始角速度大小|ω0|和初始俯仰角大小|θ0|达到一定值时,系绳张力T可能减少为零,即系绳发生松弛而不规则运动,之后运动表现无规则.由于系绳松弛后系统将不再满足第二节得出的解析关系式,故无法得出系绳松弛后不规则运动阶段的子星角速度和系绳张力随俯仰角变化关系.

对于子星初始时刻顺时针旋转(ω0>0)的情况,根据式(10)可知卫星顺时针旋转过程中科氏惯性力朝着离心方向,系绳张力将大幅减小,说明顺时针旋转过程中卫星更容易不规则运动.摆状振荡运动和自旋运动对应的子星角速度和系绳张力随俯仰角变化的关系图如图5所示.

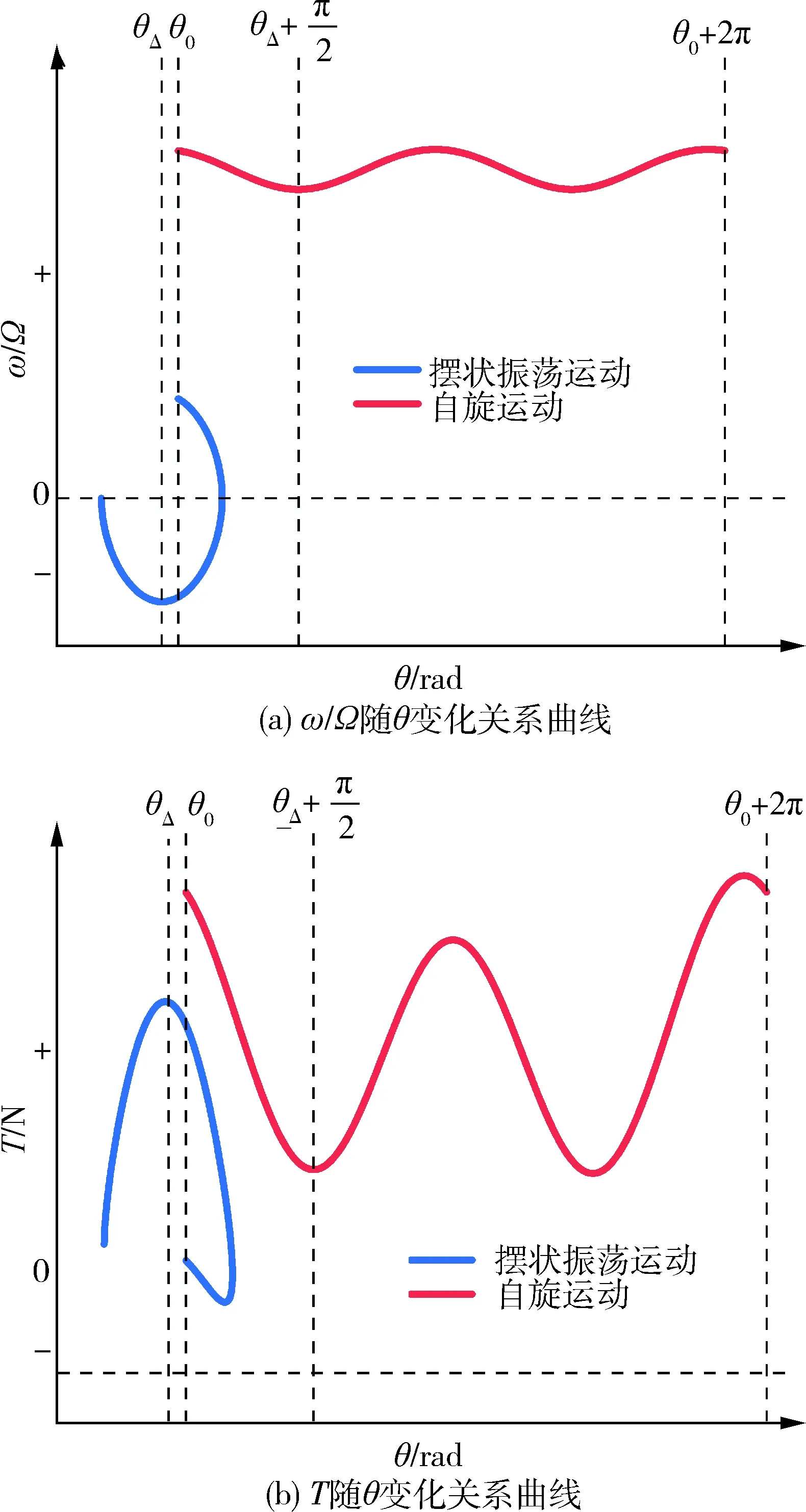
图5 初始角速度ω0>0状态下角速度和系绳张力随俯仰角关系变化曲线Fig.5 Angular velocity ω/Ω and tether force T versus pitch angle θ in initial angular velocity ω0>0

(1)摆状振荡运动(蓝色线条)

卫星初始角速度大小|ω0|小于一定值时,科氏惯性力较小,对系统张力影响不大,系绳张力持续存在,子星仍可进行摆状振荡运动.

(2)自旋轨道(红色线条)

当卫星初始角速度大小|ω0|非常大时,式(10)中项msω2L的ω次数大于项2msΩLω的ω次数,所以系统初始条件达到自旋阈值时系统向心力的增加量将大于科氏惯性力的增加量,此时系绳张力持续存在,可发生自旋运动.同样将θ=θΔ+π/2代入式(17)得到角速度ω(ω>0),将ω和θ=θΔ+π/2代入式(10),令T≥0,即可得到初始时刻顺时针旋转(ω0>0)情况下的自旋阈值.

(3)不规则运动

卫星初始角速度大小|ω0|大于一定值时,科氏惯性力较大,对系统张力影响显著,子星在到达θ=θΔ+π/2对应的极大值位置点之前系绳张力持续减少,在运动过程中系绳张力极有可能减少为零,系绳发生松弛而不规则运动,随后运动表现无规则.

由此可见,系统初始状态对动力学行为有着十分显著的影响,在执行特定太空任务时可通过解析关系式和动力学分析结论调整系统参数和初始状态参数,保证系统保持预期的运动状态.

4 数值模拟

本节对任意轨道平面外的直线型绳系卫星编队系统的动态形式进行了数值模拟,并与上节解析关系式的计算结果进行对比和分析,以验证解析关系式和动力学分析的科学性.

系统具体参数如下:母卫星和子卫星的质量分别为mM=5×103kg和mS1(S2)=2×103kg,系绳的无应变长度和刚度分别为L0=10 km和EA=2×107N,轨道高度为Ho=580 km.

取旋转角β=π/6,通过解析关系式计算和模拟仿真两种方式分别得到系统三维动力学参数域,如图6所示,图中显示了3种运动情况,即摆状振荡运动(蓝色区域)、自旋运动(红色区域)和不规则运动(黑色区域).由于参数域具有反对称性质,在此仅展示α≤0的部分,从图中可以看出旋转角、初始平面内俯仰角和初始角速度对系统的动力学行为有显著的影响.

从中各选取两组截面Γ1={(θ0,ω0/Ω0)|α=π/8}和Γ2={(θ0,ω0/Ω0)|α=-π/4}加以展示,如图7所示.可以发现,旋转角α增大,系统越容易达到自旋阈值而发生自旋.接下来,再从截面Γ1中选取3种动力学行为对应的状态点P1、P2和P3加以分析,状态点见图7(a).

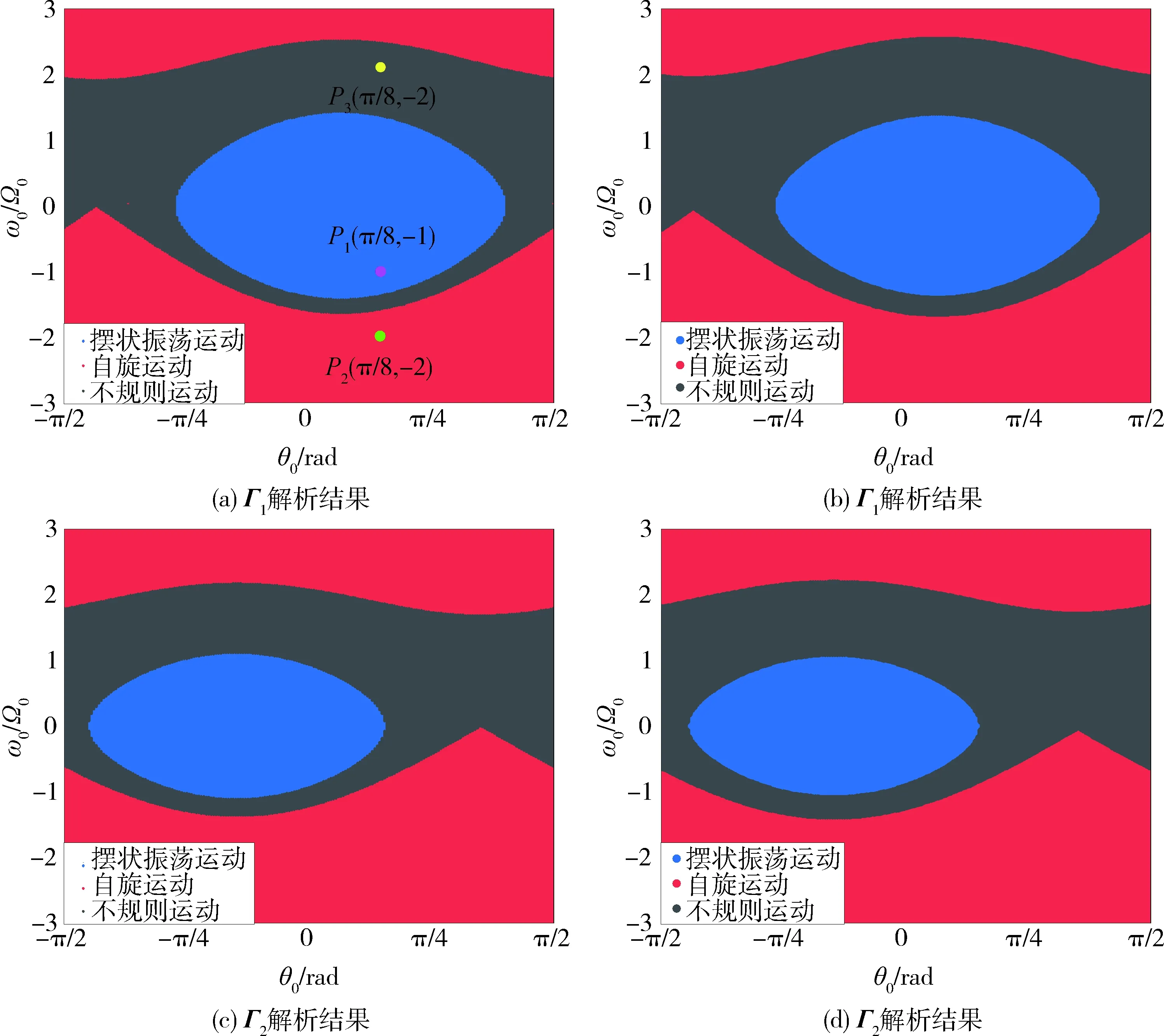
图7 Γ动力学参数域Fig.7 Parameter zone for Γ

(1)P1(π/8,-1)

该初始状态参数下系统进行摆状振荡运动,所对应的解析式计算结果和数值仿真结果如图8所示.图8(a)显示的是卫星在运动过程中俯仰角与当前角速度的关系;图8(b)为卫星在运动过程中俯仰角与系绳张力的关系,从图中可以得出该初始状态参数下卫星运动的最大俯仰角θmax=0.899 rad和最小俯仰角θmin=0.490 rad,在θ=θΔ位置处卫星达到最大角速度|ω|max=1.04Ω0且系绳达到最大张力Tmax=149.5 N;图8(c)是卫星的运动轨迹仿真图,从中可以判断系统做摆状振荡运动;图8(d)为卫星角速度比ω/Ω0和系绳长度随轨道数变化的仿真计算结果,与解析计算结果相符合.

图8 摆状振荡运动Fig.8 Pendulum-like oscillation

(2)P2(π/8,-2)

该初始状态参数下系统进行自旋运动,所对应的解析式计算结果和数值仿真结果如图9所示.图9(a)显示的是卫星在运动过程中俯仰角与当前角速度的关系;图9(b)为卫星在运动过程中俯仰角与系绳张力的关系,从图中可以得出该初始状态参数下在θ=θΔ位置处卫星达到最大角速度|ω|max=2.02Ω0且系绳达到最大张力Tmax=267.3 N,在θ=θΔ-π/2位置处卫星达到最小角速度|ω|min=1.19Ω0且系绳达到最小张力Tmin=89.5 N;图9(c)是卫星的运动轨迹仿真图,从中可以判断系统做自旋运动;图9(d)为卫星角速度比ω/Ω0和系绳长度随轨道数变化的仿真计算结果,同样与解析计算结果相符合.

图9 自旋运动Fig.9 Periodic spin motion

(3)P2(π/8,2)

该初始状态参数下子星不规则运动后运动无规则,所对应的数值仿真结果如图10所示.图10(a)是卫星的运动轨迹仿真图,从中可以判断系统做无规则运动;图10(b)为卫星角速度比ω/Ω0和系绳长度随轨道数变化的仿真计算结果.

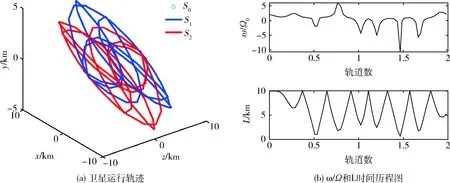
图10 不规则运动Fig.10 Irregular motion

显然,若取旋转角α=0、β=0,所建动力学模型将退化为常规轨道平面的绳系编队系统模型,对于上述解析式和分析结论同样适用.图11为常规轨道平面的绳系编队系统仿真结果图,其动力学参数域如图11(a)所示,从中选取了3种动力学行为对应的状态点Q1、Q2、Q3加以展示.对应的卫星运动仿真轨迹如图11(b～d)所示.从仿真结果来看,常规轨道系统模型可以很好地契合所建动力学模型,体现了所建模型的普适性.

图11 常规轨道绳系编队系统Fig.11 A linear tethered system in typical planes

5 结 论

在轨道平面外3颗呈直线排列的绳系编队系统中,初始状态对动力学行为有着显著的影响.通过推导初始状态与系统动力学的解析关系及对运动形式临界状态的影响,可以得到不同初始状态下系统的自旋阈值.可以发现:在初始角速度较低的情况下,系统倾向于摆状振荡运动,而初始角速度较大时,系统倾向于自旋运动;此外,运动平面旋转角越大系统越容易到达自旋阈值;子星顺时针旋转过程科氏惯性力与向心力方向相同,可能导致系绳松弛不规则运动后无规则运动.因此系统初始时刻尽量选择初始时刻逆时针高速旋转和大俯仰角以保证系统自旋稳定.数值仿真结果与解析关系计算及分析结果相符,验证了运动状态解析关系的正确性.