空间长系绳系统动力学与释放方法研究

苟兴旺，李爱军，罗拉全，王长青

（西北工业大学自动化学院，陕西西安 710072）

空间长系绳系统动力学与释放方法研究

苟兴旺，李爱军，罗拉全，王长青

（西北工业大学自动化学院，陕西西安 710072）

针对绳系载荷远距离释放问题，研究了长系绳系统释放过程的动力学特性。考虑系绳质量及面外角，建立了长绳系卫星系统动力学模型。针对空间长系绳系统展开任务要求，提出了分段多次展开的思想，将系绳的展开过程多段化，多次应用标称控制律，利用差分进化算法优化得到每段展开结束时的系绳长度。仿真结果表明，应用多次展开标称控制律不仅可以精确完成系绳的展开，而且有效抑制了长系绳展开过程中速度过大的问题，可以满足长系绳展开的速度要求。这为今后远距离系绳展开与控制提供理论参考。

空间长系绳系统；展开；动力学模型；标称控制律

空间系绳系统（TSS）［1］是指利用柔性系绳将2个或多个航天器连在一起飞行的组合体。可用于航天器轨道转移、高空大气探测、绳系交会对接、空间捕获、微重力产生等诸多场合［1-2］，已成为具有广泛应用前景的新兴空间技术。空间系绳系统的非线性动力学特性，会给系统的在轨运行带来强烈振动，特别是对柔性长系绳，由于系统包含有负阻尼的作用，动力学行为呈现不稳定的现象［3］。近年来很多学者都在探讨如何解决系绳的展开控制问题。Rupp C.C.最早提出了系绳张力控制方法［4］；于绍华讨论了绳系卫星系统二维平面运动，并提出了距离速率控制算法，基于非线性动态理论分析，实现方便且控制效果明显，但文章只对平面动力学进行了研究［5］；Pradeep利用KTC理论及其推广得到了线性张力控制律，但由于该控制律只能针对简化的线性系统，故实际控制意义不大［6］；金栋平等基于基数展开将空间系绳系统的控制转化为二次规划的最优问题，但该方法中控制项的物理意义不明显［7-8］；别列兹基提出了向垂直位置展开的单摆振荡阻尼控制律［9］，该控制律效果明显，实际物理意义明确；但他忽略了系绳的质量，对于长系绳的展开具有很大的局限性。针对长系绳系统，本文在别列兹基的基础上改进了适合于长系绳展开的标称控制律。运用分段多次展开的思想，将系绳的展开过程分为多段，多次应用标称控制律，并利用差分进化算法对每段展开结束时的长度进行了优化，避免了展开速度过快对系统造成的不利影响。数值仿真时考虑了系绳质量、初始面外角偏差等因素，仿真结果验证了该方法的有效性。

1　系绳系统动力学模型

空间系绳系统由2颗卫星组成，建立轨道运动坐标系如图1所示。

图1　空间系绳系统示意图（轨道运动坐标系）

其中，Cx0y0z0为轨道运动坐标系，坐标原点C位于母星质心处，Cx0轴沿母星向径方向，Cz0轴沿轨道平面法向并与其动量矩矢量平行，Cy0轴符合右手坐标系；Cxtytzt为系绳坐标系，Cxt轴沿着卫星拉紧系绳的反方向，Cyt轴和Czt轴相对于Cx0y0z0系的夹角为θ和β。

系绳问题非常复杂，为简化建模和分析过程，作如下假设：

1）除地球中心引力外，暂不考虑其他外部干扰力，如大气阻力和系绳电动力等；

2）子星、母星都认为质点，且母星质量远大于子星及系绳的质量，所以忽略系绳在展开过程中母星质量的变化；

3）考虑系绳既无弯曲刚度亦无扭转刚度，且系绳质量均匀分布。

根据以上假设，在轨道运动坐标系中运用拉格朗日方程建立空间长系绳系统的数学模型。

拉格朗日方程

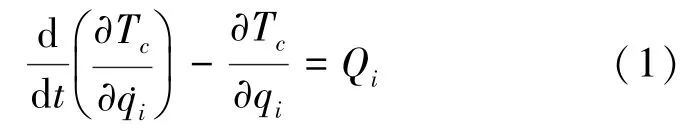
式中：Tc为系统动能；qi、q□i、Qi（i=1，2，3）是广义坐标、广义速度和广义力；面内角θ、系绳长度l和面外角β作为广义坐标。

对于长系绳系统，建模时系绳的质量不能忽略，将系绳划分为N个质量点如图2所示。

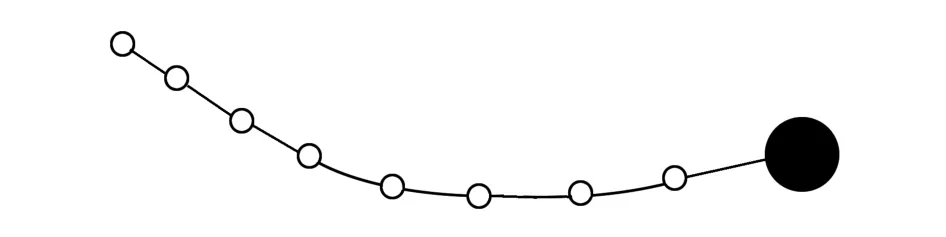
图2　长系绳模型

这样“系绳-载荷”系统的动能和势能为：

式中，k=0，1，2…N，m0=m为载荷质量，mk为第k点系绳的质量。

则第k点的运动方程为：

式中，mk=ρL/N（k=1，…，N），ρ为系绳的系密度，即单位长度上的质量，Ω为母星的轨道角速度。

N+1个点的方程求和，并且当N→∞时有：

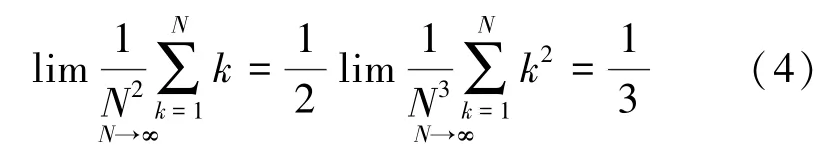
那么考虑系绳质量的空间系绳系统的运动方程为

2　长系绳展开控制律的设计

2.1一次展开标称控制律的设计

针对项目YES2中系绳系统展开的第一阶段，文献［10］中给出了一种张力控制律的表达形式：

式中，L（tk）为设定的展开长度，tk为系统展开结束的时间，m为子星的质量，a、b为依据边值条件及性能指标确定的待优化参数。

由于（6）式所示控制律设计时没有考虑系绳质量，而对长系绳系统，系绳质量就不能忽略，设计张力控制律时就必须考虑系绳的质量。因此在（6）式中加入系绳质量的修正项，得到针对长系绳的标称控制律为

在上述控制律形式的基础上，为使子星最终展开到平衡位置，即：L（tK）=LK，V（tK）=0，θ（tK）=0，θ□（tK）=0，需要寻求最优a、b参数值，使如下性能指标最小

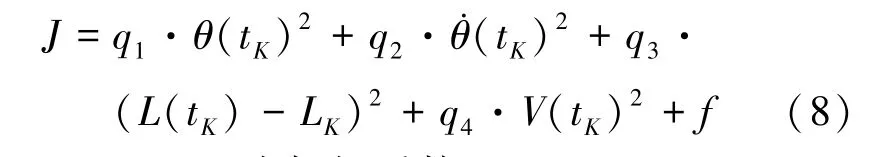
式中，q1、q2、q3、q4为加权系数；

在性能指标中，由于系绳长度的数量级远大于其他指标，故取加权系数为q1=q2=q4=1，q3= 0.001，同时为防止系绳松弛，速度V的下限要稍大于零，故加入惩罚函数f，其值为：

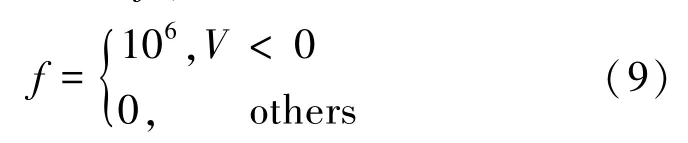
利用下山单纯形（Nelder-Mead）方法求解，可获得参数a、b的优化值。从而可获得针对长系绳的标称展开控制律。

此外，考虑系绳上承受的张力的限制，取T的上下界分别为Tmax和Tmin，则可得：

2.2多次展开标称控制律的设计

一次展开控制律，在适当的参数下，可以准确的将系绳展开到指定的终端条件。然而若系绳太长即L（tk）很大，展开开始时系绳张力T很小，会导致系绳的最大释放速度过大。而制动阶段，则需要较大的张力使速度迅速减小为零，不利于实际系绳系统的展开。

针对上述问题，本文提出将系绳分N（N＞1）阶段展开思想，将控制律（7）重复运用N次，其中L（tk）=L1，L2…LN，LN为每次展开结束后系绳的长度。这样系绳在每个阶段都有加速和制动两阶段，可以有效将系绳释放的最大速度有效的限制在一定的范围内。

在上述控制律形式的基础上，为使系统展开到终端状态同时展开时间最短，需要对L1，L2…LN进行优化，可选取如下的性能指标函数

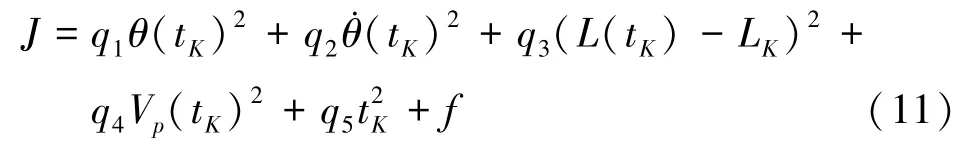
性能指标和惩罚函数q1，q2，q3，q4，f取值同（8）式，q5=1，在满足约束T＞0和V＜Vmax的条件下，利用差分进化算法可获得L1，L2…LN的参数值。

3　仿真分析

3.1仿真条件

假设TSS运行在1 000 km高度的轨道上，同时子星的释放不影响母星的轨道高度。TSS的各项参数如表1所示。

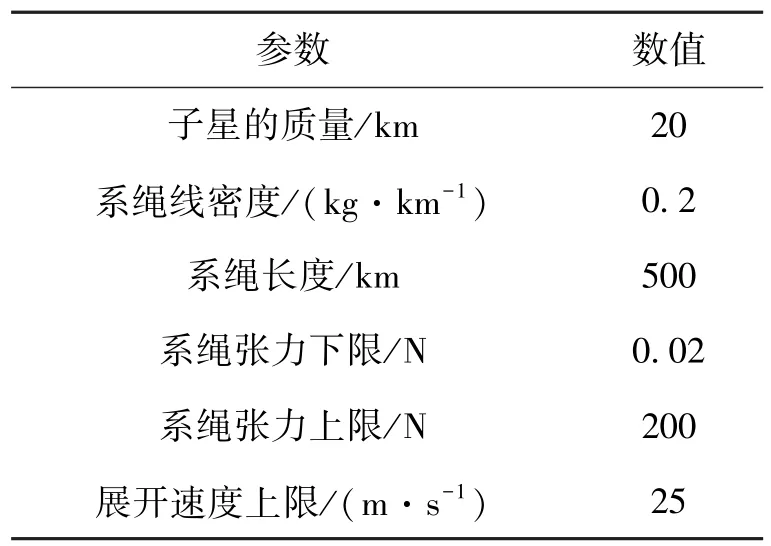
表1　TSS参数

仿真的初始条件为

3.2仿真结果与分析

一次展开控制律的参数，通过优化可获得：a= 4，b=3.7。

多次展开控制律，取分段数N=9，通过优化得每段展开结束时系绳的长度为：（L1，L2…L9）=（15，50，90，140，200，270，350，450，500）km。

图中角度单位为度，长度单位为千米，时间单位为秒。将一次展开控制律和多次展开控制律带入系统状态方程（5）中，在MATLAB平台用Runger Kutta法积分得仿真结果如图3～10所示。

从图3～10中不难发现：一次展开控制律和多次展开控制律均可以将子星展开到指定的平衡位置，初始的面外角扰动也都迅速为降为零（如图7所示）。由图10子星的运动轨迹可以看出：一次展开横向最大偏移量为124.355 km，是多次展开最大偏移量的5倍。如图6所示，展开结束时2种控制律下系绳速度都为零，然而，一次展开控制律的最大速度为：Vmax1=96.446 m/s远超出了速度限制25 m/s，系绳很容易被拉断。这主要是整个展开过程只有加速和制动2个阶段，最终导致系绳的最大速度过大，多次展开控制律的最大速度为：Vmax2= 22.048 m/s，远小于一次展开控制律的最大速度，并满足速度限制。多次展开控制律中，每段展开过程都有加速和制动阶段，有效的克服了一次展开的加速段太长导致速度过大的缺点。图3表明，多次展开控制律的最大面内角是一次展开控制律的0.8，这主要是由其展开轨迹特性决定的。

需要说明的是，分段数N的取值理论上取得越大，每段展开长度相对越短，这样运用多次展开控制律，其最大展开速度就越小，但是，这样系绳的展开时间就会越长（篇幅所限，仿真结果没有列出）。在实际工程中需考虑系绳特性时，多次展开控制律易于操作，优于一次展开控制律。

4　结 论

本文研究了空间系绳系统长系绳的展开问题，考虑系绳质量与面外运动。针对长系绳系统改进了标称展开控制律，在此基础上运用多段展开的思想，并提出了多次展开标称控制律。仿真结果表明，多次展开标称控制律不仅可以精确地完成系绳的展开，而且有效的抑制了长系绳展开过程中速度过大的问题，可以满足长系绳展开的速度要求。对于空间系绳系统多阶段展开任务，当系绳长度改变时，分为多少次展开，需根据实际工程要求来调节N的值。

［1］ 孔宪仁，徐大富.空间系绳研究综述［J］.航天器环境工程，2010，27（6）：0775-0783

Kong Xianren，Xu Dafu.The Studies of Space Tether［J］.Spacecraft Environment Engineering，2010，27（6）：0775-0783（in Chinese）

［2］ Vladimir Aslanov，Alexander Ledkov.Dynamics of Tethered Satellite Systems［M］.Russia，Woodhead Publishing Ltd，2012

［3］ 崔本廷.空间绳系的控制与应用［D］.长沙：国防科学技术大学，2006

Cui Benting.The Control and Application of Thethered System［D］.Changsha，National University of Defense Technology，2006 （in Chinese）

［4］ Rupp C C.A Tether Tension Control Law for Tethered Satellite Deployed along Local Vertical［R］.Marshall Space Flight Center，NASA TM X-64963，1975

［5］ 于绍华.绳系卫星系统二维平面运动和常规动力学［J］.宇航学报，2000（4）：15-24

Yu Shaohua.Regular Dynamics of In-Planar Motion of Tethered Satellite System［J］.Journal of Astronautics，20004：15-24（in Chinese）

［6］ Pradeep S.A New Tension Control Law for Deployment of Tethered Satellites［J］.Mechanics Research Communications，1997，24（3）：247-254

［7］ Jin D P，Hu H Y.Optimal Control of a Tethered Subsatellite of Three Degrees of Freedom［J］.Nonlinear Dynamics，2006，46：161-178

［8］ 文浩，金栋平，胡海岩.基于微分包含的绳系卫星时间最优释放控制［J］.力学学报，2008，40（1）：135-140

Wen Hao，Jin Dongping，Hu Haiyan.Time-Optimal Deployment of a Tethered Subsatellite Based on Differential Inclusion［J］. Chinese Journal of Theoretical and Applied Mechanics，2008，40（1）：135-140（in Chinese）

［9］ Beletsky V，Levin E M.Dynamics of Space Tether Systems［M］.Russia：Amer Astronautilcal Society，1993

［10］扎伯罗特诺夫·尤里著.空间系绳系统运动动力学与控制导论［M］.王长青，译.科学出版社，2013

Zablotnov Yuriy.Introduction to Dynamics and Control in Space Tether System［M］.Wang Changqing Translator.Beijing，Science Press，2013（in Chinese）

Research on Dynamics and Deployment Method for Long Space Tether System

Gou Xingwang，Li Aijun，Luo Laquan，Wang Changqing
（Department of Automatic Control，Northwestern Polytechnical University，Xi′an 710072，China）

This paper studies the control strategy of the deployment for long space tether system.Dynamic characteristic of the long tethered satellite is researched and analyzed in the deployment process.The mathematical model is established through Lagrange Equation，considering the mass of the tether and the out-plane angle of the sub-satellite.Multi-deployment method is proposed according to the requirements of the deployment of the long space tether system.The deployment process is divided into several sections，and the length of tether in each section is optimized with differential evolution algorithm.The nominal control low is applied in every section.Numerical simulation results prove that the proposed control law could not only deploy the sub-satellite to the right location，but also reduce the maximum velocity of deployment of sub-satellite effectively.Multi-deployment method can satisfy the requirement of long tethered satellite deployment.It has theoretical value and can be used in the further research.

long space tether system；deployment；dynamic model；nominal control low

V448.2

A

1000-2758（2015）06-0966-05

2015-03-17

2011年度国家国际科技合作专项资助与陕西省科学技术研究发展计划项目（2013KW09-02）资助

苟兴旺（1979—），西北工业大学博士研究生，主要从事飞行器控制与仿真的研究。