一种细粒度流水化控制的FPU集成方法

陈庆宇，吴龙胜

（西安微电子技术研究所，陕西西安 710065）

一种细粒度流水化控制的FPU集成方法

陈庆宇，吴龙胜

（西安微电子技术研究所，陕西西安 710065）

解决了在RISC处理器中嵌入高精度FPU的问题，提出一种细粒度的基于集中控制和分段数据处理的扩展双精度FPU集成方法，该方法通过细分浮点指令的执行状态，然后以执行状态为基本粒度生成与之对应的FPU控制信息，最后根据控制信息分段处理目标操作数，并通过流水化的形式实现数据的回写。基于一款SPARC V8型微处理器对上述方案进行了设计实现、仿真验证及分析。结果表明，该FPU集成方法与公开文献的方案相比，浮点指令关键路径缩短61%，硬件消耗减小16. 9%，浮点计算效率提高1.7倍，可用于将扩展双精度FPU集成到RISC处理器中，并使两者高效协同运算。

FPU；协同运算；细粒度；集中控制；流水回写

当前，飞行控制、工业应用及多媒体技术等领域对嵌入式微处理器的浮点性能提出了更严苛的要求［1］。然而ARM、MIPS、SPARC V8、PowerPC等主流RISC微处理器仅支持单、双精度的浮点运算［2-5］，若需要更高精度的数据则只能依靠软件模拟浮点运算，这种方式使处理器浮点性能降低数十倍［6-7］。为了满足未来航空航天及工业领域对数据精度和计算性能的要求，国内外研究学者近年已经进行了诸多研究。

文献［8-9］介绍了超高精度FPU的实现方案，赵勇等［10］利用存储在ROM中的浮点微指令码将80位FPU嵌入到x86处理器内部。微指令码的读取消耗处理器时间，降低浮点执行效率，同时由于处理器体系结构的差异，该方案很难移植到采用流水线技术的RISC处理器中。

文献［7，11-12］降低了FPU与处理器的耦合度，将FPU作为片内总线的从单元，以访存指令控制FPU的计算过程。上述方案需要软件干预运算，增加了片内总线的访问冲突，造成单个FPU效率极低，虽然通过设计FPU专用的数据总线、改进FPU与处理器交互方式等措施改善了计算效率，但结果依然不理想。

针对FPU嵌入RISC处理器的问题国内外进行了很多研究［8-12］，但多数方案均需软件干预，且不支持超高精度FPU（80位或更高）在RISC处理器中的集成。针对此问题，本文提出一种细粒度的集中控制和分段处理方法，首先利用状态机标识浮点指令执行状态，然后产生与执行状态对应的FPU控制信息，并将回写所需的控制信息通过流水段间寄存器向后级传递，最后在处理器的不同流水段依据控制信息对FPU输出结果进行分段寄存，并以流水化的形式将目标操作数写回寄存器堆。与其他研究相比，本文的主要贡献如下：

1）首次公开了超高精度FPU植入RISC流水线处理器的方法，基于此方法实现了80位FPU的集成，且无须更改已有的处理器设计。

2）本文提出的集成方法全部硬件实现，FPU与处理器核紧密耦合，避免了软件干预浮点运算，FPU执行效率高。

本文介绍了高精度FPU集成方案的技术背景，紧接着提出一种面向RISC流水线处理器的、细粒度集中控制和分段处理数据的FPU集成方法，并基于该方法将一个扩展双精度的FPU（80位，Meiko接口，兼容Intel浮点协处理器）集成到一款5级流水的SPARC V8型微处理器中［13］，最后将该方案的实现及验证结果与已有方案进行了对比分析，并对本文进行了总结。

1　控制算法及实现

本文提出的FPU集成方法在实现过程中仅在处理器不同流水段增加FPU的控制逻辑，避免了对处理器的访存单元、冒险检测、异常处理等模块的更改。下文以典型5级流水RISC处理器［14］为例说明本文所述FPU集成方法的控制算法及实现，其中细粒度集中控制在处理器译码段（ID）实现，流水化分段数据处理涉及流水线的执行段（EX）、存储访问段（MA）及回写段（WB）。

1.1细粒度控制原理

浮点指令（FPop，floating-point operate）主要实现浮点数据的类型转换和算术运算，其分类如表1所示，源和目标操作数精度类型分别以S和D标志，均包括整型I、单精度S、双精度D及扩展双精度Q，SDDS指源操作数为双精度且目标操作数属于单精度的浮点指令。根据操作数精度类型组合，将15种指令类型分为S、D、Q 3类，其中S类（single FPop）操作数位宽为32，D类（double FPop）使用至少一个64位操作数且无80位操作数，Q类（quad FPOP）包含至少一个80位操作数。本文通过细分D和Q类指令的执行状态，利用不同状态以流水化形式实现宽位操作数在窄位浮点寄存器堆中的读写访问。

表1　浮点指令操作数精度类型组合

利用状态机解析浮点指令实现细粒度控制。如图1所示，状态机中4种S状态与3类指令类型对应，X.S0属于S、D和Q类指令的共享状态，在S0状态下对指令类型细化，若当前指令为single FPop或者存在数据或控制冒险，则维持S0状态；若当前指令为double FPop，则流水使能信号有效时（hold= 1），进入D.S1状态；若当前指令为Quad FPop，则流水使能hold=1时，进入Q.S1状态；在非S0状态处理器取指模块阻止PC更新，防止新的指令进入ID段。控制算法以图1状态机状态为基本粒度产生对应的FPU控制信息，并将回写信息向下一级流水传递，为后续的流水化分段数据处理提供依据。

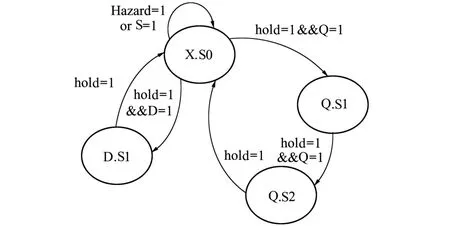
图1　细粒度控制状态机

源操作数的控制算法如图2a）所示，regfile［rs］指源操作数地址rs指定的寄存器堆中的数据，图中并未就FPU计算所需的2个源操作数进行区分。控制算法在S0状态下等待流水线中冒险情况消失，之后将regfile［rs］传递给FPU输入fpui.rs的低32位；在S1状态下，将regfile［rs+1］赋值给fpui.rs的中间32位；在S2状态下，将regfile［rs+2］赋值给fpui.rs的高16位；同时控制算法依据源操作的精度类型，待源操作数准备就绪后启动FPU运算（fpui. start=‘1’）。

目标操作数的读写控制算法如图2b）所示，pipeline为流水段间寄存器的数据结构。控制算法规定S2、S1及S0的等级依次降低，并利用高等级的状态回写FPU输出的目标操作数低位数据（低位数据对应高地址）。在S0、D.S1、Q.S1和Q.S2状态下比较目标操作数和源操作数的位宽，利用位宽这一基准条件产生FPU输出结果回写所需的写使能和对应地址等控制信息，并通过流水段间寄存器pipeline向后传递。结合表1以D.S1为例进行说明，可进入该状态的5类指令中只有SDDI和SDDS的目标操作数位宽小于源操作数位宽，根据利用高等级的状态回写FPU低位数据的原则，在D.S1状态下置目标操作数写使能rd-wen有效并给出正确的写地址。

图2　基于状态的细粒度控制机制

1.2流水化处理数据机制

FPU一旦计算完成，流水线处理器的EX段、MA段及WB段对FPU的输出结果分段寄存，之后通过pipeline向后传递，最终写入寄存器堆。分段处理算法的进一步描述如图3所示，首先判断FPU输出结果，若异常则废除回写动作并向异常处理模块提交异常信息；若结果正常则进一步判断指令类型，并根据状态信息pipeline.state对FPU输出的目标操作数进行分段寄存，分段寄存后的数据与图2b）产生的写地址和写使能一一对应。以Q类指令为例，目标操作数小于源操作数位宽的指令仅有SQDI、SQDS、SQDD 3类，其中SQDI和SQDS的目标操作数宽度32bits，根据利用高等级的状态回写低位数据的原则，EX段在“10”状态下将FPU输出保存到pipeline寄存器；对于64位输出的SQDD，EX段在“10”状态下保存FPU的低32位输出，MA段在“01”状态下保存FPU的高32位输出；除上之外的Q类指令均包含80位目标操作数，则EX段在“10”保存FPU输出的80位操作数的低16位；MA段在“01”状态保存80位目标操作数的次32位；WB段的“00”状态保存80位FPU输出结果的高32位。

图3　数据分段处理流程图

1.3 FPU集成方案实现

SPARC V8是一种开源的RISC体系结构［15］，在欧洲及我国的航空航天领域应用广泛，本文选择该架构进一步详述细粒度FPU集成方法在RISC流水线处理器中的实现。一款80位Meiko接口的扩展双精度FPU与处理器核的耦合方案示如图4所示，处理器核为典型的RISC 5级流水线，ID段的细粒度控制模块实现2.1节所述控制算法，并通过段间寄存器pipeline向后级流水传递分段回写FPU输出结果所需的控制信息；EX、MA及WB段的分段处理模块依据图3所示的流程实现目标操作数向浮点寄存器堆的流水化回写。

图4　扩展双精度FPU与处理器核的耦合示意图

2　实现及测试结果

基于Cadence公司的eRM（ereuse methodology）对本文提出的细粒度扩展双精度FPU集成方法进行仿真验证，验证工具及仿真器采用specman elite和modelsim simulator，处理器浮点结果与验证环境中斯坦福大学开发的TestFloat进行对比，结果表明采用本文方案的处理器浮点功能正确，图5a）、图5b）分别给出了典型的时序图，图5a）为SQDQ类指令（源和目标操作数均为扩展双精度）时序图，ID段利用3个时钟周期取得源操作数，并启动FPU计算，WB段利用状态“00”、“01”和“10”实现流水化写回。图5b）为SSDQ类浮点指令（单精度源操作数，扩展双精度目标操作数）的时序图，ID段第1个时钟周期启动FPU计算，在后续2个周期内产生目标操作数对应的写使能和地址，待计算完成后，各流水段根据pipeline的控制信息分段寄存FPU输出，最后在WB级实现流水化回写。

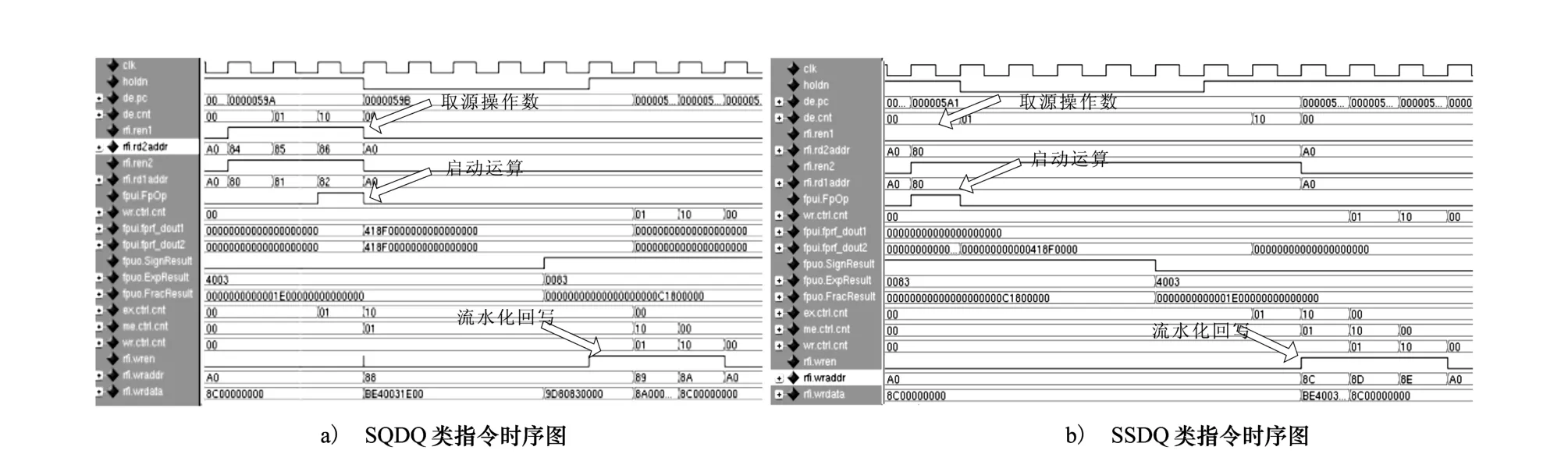
图5　本文集成方法的时序图

在功能正确的基础上，本节分析了细粒度的FPU集成方法的综合及测试情况。本文提出的方法以执行状态为基本粒度产生控制信息，这种控制逻辑的细粒度化最大程度上降低了复杂度，基于SMIC 0.18 μm工艺库的关键路径延时仅2.3 ns，与基于浮点指令码的方案［10］相比降低了61%；由于采用了流水化形式回写目标操作数，复用了流水段中的诸多硬件资源，利用文献［7］同样的FPGA器件对本文方法进行综合，硬件消耗如表2所示，与Joven等完成的FPU为片内总线从机的Cortex-M1方案相比［7］，本文方案LUTs的使用减少16.9%；与处理器紧耦合的GRFPU LITE实现相比［11］，本文LUT、寄存器的消耗分别增加9.6%和9%，主要原因是GRFPU LITE仅实现双精度FPU的集成，而本文方法适用于单、双、扩展双精度FPU的集成。

表2　不同方案硬件消耗的对比

图6　浮点计算效率的对比

3　结 论

最后对浮点效率进行了评估，并与已公开的方案［7，11，16］进行了对比，结果如图6a）、图6b）所示。LEON3 FPU需要软件参与浮点运算，浮点运算效率较低，单、双精度的浮点运算均需173个时钟周期；瑞典Gaisler研究所的GRFPU和GRFPULITE将FPU嵌入到处理器核内部，实现处理器与FPU的紧密耦合，需要近30个时钟周期完成单、双精度的浮点运算；Joven等完成的Cortex-M1方案将FPU作为处理器的总线从机，通过改进两者交互方式，需约15～30个时钟完成浮点指令的执行；而本文方法以基于时钟的指令执行状态为基本粒度产生FPU的控制信息，通过全硬件方式将FPU植入处理器核，导致两者之间的通信开销几乎可以忽略，仅需要9～10个时钟完成单、双精度的浮点运算，效率超过Cortex-M1至少1.7倍。图6c）进一步给出了基于本方法的V8型处理器扩展双精度的浮点运算时的时钟开销，比软件模拟浮点运算效率提高20～100倍［7，11］。

［1］ Bailey D H.High-Precision Floating-Point Arithmetic in Scientific Computation［J］.Computing in Science&Engineering，2005，7（3）：54-61

［2］ 王重阳.单、双、扩展精度自适应浮点乘、除和开方运算单元的实现［D］.北京：华北电力大学，2011

Wang Chongyang.Realization of Adaptive Floating-Point Multiplication，Division and Square Root Unit for Single，Double and Extended Precision［D］.Beijing：North China Electric Power University，2011（in Chinese）

［3］ Aeroflex.UT699 LEON 3FT/SPARC V8 Microprocessor Functional Manual［M］.Aeroflex Inc，2012

［4］ Kane G，Heinrich J.MIPS RISC Architectures［M］.Prentice-Hall，Inc，1992

［5］ Boersma M，Kroner M，Layer C，et al.The POWER7 Binary Floating-Point Unit［C］∥2011 20th IEEE Symposium on Computer Arithmetic（ARITH），2011：87-91

［6］ Ramakrishnan A，Conrad J M.Analysis of Floating Point Operations in Microcontrollers［C］∥Southeastcon，2011 Proceedings of IEEE，2011：97-100

［7］ Joven J，Strict P，Castells-Rufas D，et al.HW-SW Implementation of a Decoupled FPU for ARM-Based Cortex-M1 SoCs in FPGAs［C］∥2011 6th IEEE International Symposium on Industrial Embedded Systems（SIES），2011：1-8

［8］ Schwarz E M，Schmookler M，Trong S D.FPU Implementations with Denormalized Numbers［J］.IEEE Trans on Computers，2005，54（7）：825-836

［9］ Trong S D，Schmookler M S，Schwarz E M，et al.P6 Binary Floating-Point Unit［C］∥IEEE Symposium on Computer Arithmetic，2007：77-86

［10］赵勇，张盛兵，王党辉.微处理器浮点IP核集成设计［J］.微电子学与计算机，2006，23（7）：129-133

Zhao Yong，Zhang Shengbing，Wang Danghui.The Integration of Floating Point IP in Microprocessor Design［J］.Microelectronics&Computer，2006，23（7）：129-133（in Chinese）

［11］Gajjar N，Devahsrayee N M，Dasgupta K S.Scalable LEON 3 Based SoC for Multiple Floating Point Operations［C］∥2011 Nirma University International Conference on Engineering（NUiCONE），2011：1-3

［12］杜学亮，金西.向量浮点协处理器VFP-A的设计和验证［J］.微电子学，2009，39（5）：597-601

Du Xueliang，Jin Xi.Design and Verification of Vector Floating Point Coprocessor VFP-A［J］.Microelectronics，2009，39（5）：597-601（in Chinese）

［13］Gaisler J.The LEON-2 Processor User′s Manual［M］.Sweden，Gaisler Research Inc，2003

［14］Hennessy J L，Patterson D A.Computer Architecture：A Quantitative Approach［M］.Holland，Elsevier，2012

［15］Internationa S.The SPARC Architecture Manual Version 8［M］.SPARC International Inc，1998

［16］Gaisler J，Catovic E，Isomaki M，et al.GRLIB IP Core User′s Manual［M］.Gaisler Research，2007

A Method of FPU Integration Based on Fine-Grained Pipeline Control

Chen Qingyu，Wu Longsheng
（Xi′an Microelectronics Technology Institute，Xi′an 710054，China）

Double-precision floating-point can hardly satisfy the accuracy requirement of contemporary scientific computing.It deserves further study about how to get the higher precision FPU embedded into the RISC processor and about how to make an effective collaborative computing between them.A fine-grained integration method of extended double-precision FPU is proposed in this paper；it is based on centralized control and segmented data processing.The method finely differentiates the execution status of floating instructions and generates the FPU control information corresponding to execution status of floating-point instructions in fine-grain.Then，destination operands are segmentedly processed and written back register is implemented and the implementation is explained with a flowchart.An SPARC V8 processor based on the proposed mechanism has been implemented，verified and analyzed.The results and their analysis show preliminarily that the critical path of floating instructions decreases 61%，hardware consumption declines 16.9%and the floating-point calculation efficiency increase 1.7 times.

algorithms，calculations，computer architecture，computer hardware，controllers，cost reduction，data processing，digital arithmetic，efficiency，exchange coupling，flowcharting，microprocessor chips，real time control，scalability，schematic diagrams，state estimation，time delay；centralized control，collaboration computing，fine-grain，FPU，pipeline write-back

TP302.1

A

1000-2758（2015）06-1049-06

2015-04-24

陈庆宇（1988—），西安微电子技术研究所博士研究生，主要从事高性能飞行控制SoC设计及系统级可靠性研究。