大型航天结构在轨组装阶段作动器布局优化

邬树楠, 周威亚, 叶 哲, 李庆军*, 邓子辰

1. 中山大学航空航天学院, 深圳 518107 2. 大连理工大学航空航天学院, 大连 116024 3. 西北工业大学航空学院, 西安 710072

0 引 言

随着航天技术的快速发展以及日益增长的太空任务需求,航天器的尺寸朝着大型化的方向发展[1-2].受火箭推力及整流罩包络等条件制约,超大型航天结构将突破传统制造模式,更适用于“模块化设计制造-在轨组装成型”的新模式.在模块化设计过程中,通常将航天结构设计为多个配置有敏感器与作动器的子结构[3].在轨组装阶段,航天结构中模块化子结构会不断增加,用于组装的作动器数目也会逐渐增多.然而,受成本等因素的限制,不可能对每个组装子结构布置大量的作动器.因此,开展大型航天结构在轨组装阶段的作动器优化配置研究具有重要的应用价值.

由于大型航天结构的在轨组装是一个逐渐变化的过程,组装阶段其构型与参数不断改变.因此,大型航天结构组装阶段的作动器优化配置不同于在轨运行阶段.目前,国内外诸多学者对于大型航天结构作动器优化配置的研究多集中于在轨运行阶段构型不变的情况.如文献[4]研究了太阳能发电卫星姿态传感器的优化配置.文献[5]基于粒子群算法研究了桁架结构作动器的优化配置.文献[6]结合遗传算法研究了空间智能桁架的传感器与作动器的优化配置.以上这些关于作动器优化配置的研究对于在轨组装阶段“离散渐增”的大型航天结构的作动器优化配置并不适用.目前对于组装阶段大型航天结构作动器的优化配置问题研究较少,已有的一些研究工作多为大型航天结构在轨组装序列规划[7]、在轨组装阶段的动力学建模与主动控制等[8].此外,在其他领域也有一些有趣的研究,文献[9]指出为了保证施工阶段桥梁结构的稳定与精准,需要对施工阶段的传感器进行优化配置.文献[10]开展了大跨度型钢混凝土桁架施工阶段监测方案的研究,并指出大跨度结构施工阶段存在的问题和进行施工过程监测的必要性.然而在太空环境中组装大型航天结构不同于地面桥梁施工过程,组装过程中会受到各种空间摄动的影响,同时由于太空中弱阻尼环境以及组装阶段空间结构缺少支撑,组装阶段由外部激励和组装碰撞等引起的结构振动很难自行衰减.因此,为了保证组装任务的顺利进行,需要对组装阶段的航天结构进行主动振动抑制.若对每个组装子结构的作动器进行相同的配置,则无法充分发挥作动器的性能,也即无法实现在轨组装阶段大型航天结构的最优控制.此时,如何基于有限数量的作动器,对其位置进行合理安排,保证每个组装阶段作动器的最优配置,实现在轨组装过程中大型航天结构的振动控制,需要进一步研究讨论.

针对上述问题,本文结合大型航天结构模块化的特点,提出一种在轨组装阶段作动器布局的分布式优化策略.以多旋转关节式空间太阳能电站在轨组装为背景[11],根据在轨组装阶段航天结构“离散渐增”的特点,建立各组装阶段配置有压电主动杆的桁架结构动力学模型,结合天牛须搜索算法对粒子群算法进行改进.然后依据系统的可控Gramian矩阵定义作动器配置的优化准则,采用改进的混合粒子群算法进行大型航天结构在轨组装阶段作动器的分布式优化配置.所设计的分布式优化策略能够保证各组装阶段作动器的最优配置.最后给出算例仿真,验证所提方法的有效性和可行性.

1 组装阶段的作动器优化设计方法

大型航天结构由多个子结构在轨组装而成,每个子结构采用模块化设计、批量化生产并集成有作动器与敏感器.受多智能体理论的启发,文献[12]引入智能子结构的概念来定义这种模块化子结构,并提出了分布式一致性控制方法以抑制组装过程中的结构振动.随着在轨组装的进行,航天结构逐渐由分散统一为整体,这种“构型渐增”的特点与分布式控制有较为天然的一致性,因而在轨组装阶段作动器布局也适用于分布式优化策略.受成本等因素的限制,不可能对每个组装子结构布置大量的作动装置,并且由于每个组装阶段航天结构的构型不同,不同布局的作动器所带来的控制效果也有所不同.若想实现在轨组装过程中的最优控制,需要对各组装阶段大型航天结构的作动器布局进行优化.大型航天结构多采用桁架作为支撑结构,而压电主动杆作为桁架结构的主要作动装置,其安装位置的不同也会对结构特性产生不同的影响[13].若实现组装过程中压电主动杆的优化配置,不但能够有效地完成组装阶段桁架结构的振动主动控制,确保组装过程中航天结构稳定、同时提高组装效率.因此,本文以带有压电杆的桁架结构为研究对象,开展大型航天结构在轨组装阶段的作动器优化配置研究,基于智能子结构的定义并考虑服务于分布式振动控制[12],提出一种适用于大型航天结构组装阶段的作动器分布式优化配置方法,如图1所示.

图1 桁架结构在轨组装及作动器配置示意图Fig.1 Schematic diagram of on-orbit assembly truss structure and actuator configuration

具体优化步骤如下:

1)首先根据组装任务要求和航天结构的尺寸构型,将其划分为N个待组装的子结构,并确定子结构的组装顺序;

2)建立当前组装阶段含有压电主动杆的桁架结构动力学模型;

3)对当前组装阶段,桁架子结构中压电作动器的位置进行优化配置,并进行下一阶段子结构的组装;

4)在第3步的基础上,对下一组装阶段的子结构进行作动器优化配置;

5)重复步骤3和4,逐步完成大型航天结构在轨组装阶段作动器布局的分布式优化.

2 组装阶段作动器布局的分布式优化

2.1 桁架结构动力学模型

为了实现大型航天结构组装阶段的作动器优化配置,需要先给出桁架子结构的动力学模型.桁架子结构由普通杆和压电主动杆[13]组成,如图2所示.压电作动器由压电陶瓷堆、预紧弹簧、球铰、连接杆等组成,如图3所示.

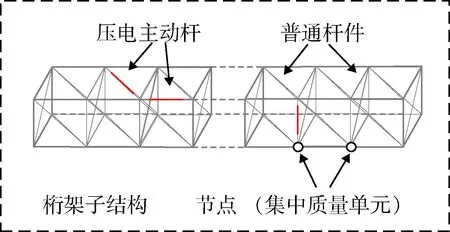
图2 桁架子结构简化模型Fig.2 Simplified model of space truss substructure

图3 压电作动器结构示意图Fig.3 The sketch map of piezoelectric actuator

为了便于建立压电作动器的动力学模型,将其简化为“压电叠堆-弹簧”结构.采用有限元方法,由拉格朗日方程可求得压电作动器的动力学方程

(1)

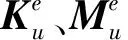
在此基础上,建立包含有压电作动器的桁架子结构的动力学模型

(2)

式中:i表示第i个子结构,qi∈Rni×1为桁架子结构的节点位移矢量,Mi∈Rni×ni、Ci∈Rni×ni和Ki∈Rni×ni分别为桁架子结构的质量矩阵、阻尼矩阵和刚度矩阵,其中阻尼为瑞利阻尼;Ldi∈Rni×nb为桁架子结构扰动作用力位置矩阵;wdi∈Rni×1为桁架子结构受到的外部扰动;Lci∈Rni×nb为桁架子结构压电作动器的位置矩阵,uci∈Rni×1为桁架子结构作动器产生的控制力向量;ni、nb分别为桁架子结构系统的自由度和压电作动器数目.

结合图1给出的桁架结构在轨组装示意图,通过在轨装配可得组装阶段一端固定的整体桁架结构的动力学模型

(3)

考虑系统的前nc阶模态,做模态坐标变换

q=Φcηc

(4)

式中,Φc为前nc阶模态阵型向量组成的模态矩阵,ηc为前nc阶模态坐标.

(5)

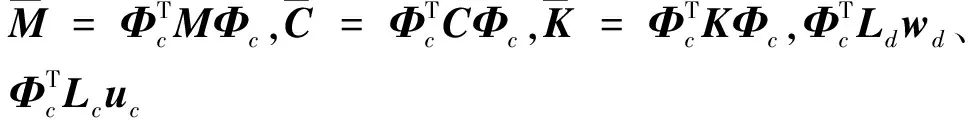
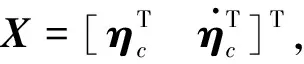
(6)

2.2 优化准则

本文按如下定义控制能量最小化:

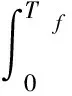
(7)

由文献[14]可以得到

(8)

式中,Y0为初始时刻的系统状态,YTf为Tf时刻系统的状态.将式(8)代入式(7)中,变换得到

J=(eATfY0-YTf)T[Wc(Tf)]-1(eATfY0-YTf)

(9)

式中,

(10)

Wc(Tf)被称为可控的Gramian矩阵,Wc(Tf)的范数越高,系统的输入能量越小.对于稳定的系统,当Tf=∞时,Gramian矩阵Wc(Tf)与恒定常值Gramian矩阵Wc关系如下:

Wc(Tf)=Wc-eATfWceATTf

(11)

式中,

(12)

由式(9)可以看出,最小化控制能量J等同于最大化一个与时间Tf无关的可控Gramian矩阵Wc的范数,同时Wc满足Lyapunov方程

(13)

由式(13)可以看出,Wc的范数大小和系统状态矩阵A和作动器输入矩阵Bc有关.当控制系统确定后,A矩阵是固定不变,作动器输入矩阵Bc与作动器的位置有关.因此,可以通过改变作动器输入矩阵Bc来使矩阵Wc的范数最大.关于作动器的优化准则有许多研究,本文结合系统的可控Gramian矩阵,采用文献[14-15]中定义的作动器优化准则,进行组装中桁架结构作动器的位置优化.在这种准则中,目标函数数值越高,代表系统的可控度越好,也即作动器的位置越好.准则形式如下:

(14)

3 改进的混合粒子群算法

3.1 混合粒子群算法

粒子群(PSO)算法是一种群体智能的优化算法,源于对鸟群觅食行为的研究.PSO算法是从这种生物种群行为特征中得到启发并用于求解优化问题的,算法中每个粒子都代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值.粒子的速度决定了粒子移动的方向和距离,速度随自身及其他粒子的移动进行动态调整,从而实现个体在可解空间中的寻优.本文采用带压缩因子的混合粒子群算法(HPSO),速度和位置更新公式如下:

Vid(t+1)=χ{ωVid(t)+c1r1(Pid(t)-Xid(t))+
c2r2(Ggd(t)-Xid(t))}

(15)

Xid(t+1)=Xid(t)+Vid(t+1)

(16)

(17)

式中:ω为惯性权重,Pi为个体极值,Gg为群体极值;d=1,2,…,D,i=1,2,…,m;Vi为粒子的速度;r1、r2是分布于[0,1]区间的随机数.c1、c2为加速度因子是非负的常数且c1+c2>4.为了进一步调整粒子速度在寻优过程中的变化,我们依然保留了权重系数,惯性权重的更新策略为

ω=ωstart-(ωstart-ωend)(t/tmax)2

(18)

式中,ωstart表示初始惯性权重,ωend为迭代至最大步数时的惯性权重,t表示当前迭代步数,tmax表示最大迭代步数.

3.2 天牛须搜索算法

天牛须(BAS)搜索算法是依据天牛觅食启发而开发出的智能优化算法[16].自然界中天牛在进行觅食时,主要依靠两根触角对于气味敏感度的分析进行食物的寻找.若右侧触角接收的气味强度大,那么天牛飞向右侧,反之则飞向左侧.因此,可以将空间中的食物气味等效为一个函数,该函数在n维空间中每个点的值都不一样.天牛的主要目的就是找到食物的位置,即气味最大的点.因此可以将天牛觅食问题抽象为一个求解求n维模型优化问题,简化模型如图4所示.

图4 天牛简化模型Fig.4 Simplified model of Longicorn

假设天牛随机向一个方向爬行

(19)

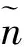
用d0表示左须和右须之间的距离,若用x表示左右须的质心位置,则xl,xr可以表示为如下形式:

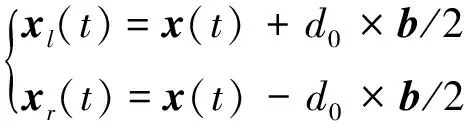
(20)

式中,xl代表搜索区域左侧,xr代表搜索区域右侧.

用f(xl)和f(xr)代表左右位置的适应度值,通过下式迭代更新天牛的位置:

x(t+1)=x(t)-δ(t)×b×
sign(f(xr(t))-f(xl(t)))

(21)

(22)

d0=δ(t)/c3

(23)

为进一步提高标准天牛须搜索算法的性能,对其参数进行优化,将其固定步长的搜索改为变步长搜索[17],变化步长为

(24)

式中,r0和r1为常数.

3.3 改进的混合粒子群算法

粒子群算法通过搜索个体极值和全局极值来完成搜索寻优,虽然操作简单,但搜索精度不够高.随着迭代次数的增加,在种群收敛集中的同时各粒子会逐渐相似,从而丧失多样性,容易在搜索过程中陷入局部最优.BAS算法作为一种单体搜索算法,全局搜索能力强,收敛速度快.若将BAS算法的搜索机理引入到HPSO算法中,赋予HPSO算法中的每个粒子拥有感知自身左右两侧位置的能力.在粒子更新过程中,通过对比左右两侧粒子适应度大小,并将比较结果加入到粒子更新过程中,提高每个粒子对自身的认知能力,进而提高HPSO算法的全局搜索能力和收敛速度.

基于天牛须搜索算法改进的混合粒子群优化算法(BAS-HPSO)中的粒子更新公式如下:

vb(t)=-δ(t)×b×
sign(f(Xidr(t))-f(Xidl(t)))

(25)

Vid(t+1)=χ{ω(t)Vid(t)+c1r1(Pid(t)-Xid(t))+
c2r2(Pgd(t)-Xid(t))}+vb(t)

(26)

Xid(t+1)=Xid(t)+Vid(t+1)

(27)

式中,vb是BAS-HPSO算法生成的粒子触须指向.

上述BAS-HPSO算法的实现过程如下:

1)设置算法参数,随机生成初始种群并计算初始种群中粒子的适应度;

2)粒子触须指向更新,计算每个粒子左右触须的适应度,按式(25)更新粒子触须指向;

3)粒子速度更新,按式(26)更新粒子速度;

4)粒子位置更新,按式(27)更新粒子位置;

5)计算每个粒子的适应度值;

6)对每个粒子,用新粒子适应度值与个体极值比较,如果新粒子适应度值优于个体极值,则对个体最优解进行更新;

7)对每个粒子,用新粒子适应度值与全局极值比较,如果新粒子适应度值优于全局极值,则对全局极值进行更新;

8)根据式(25)～(27),更新粒子的位置和速度;

9)判断是否达到最大迭代次数,若未达到则返回第2步;若达到最大迭代次数则输出优化结果.

4 仿真校验

以在轨组装阶段一端固定桁架结构的作动器位置优化为研究内容,进行数值仿真.假设桁架结构包含4组子结构,每组子结构配置有3根压电主动杆.组装阶段作动器布局的分布式优化分为4次进行,具体优化流程参照第1节图1所示.桁架结构的参数见表1,用于振动控制的主动杆参数见表2.

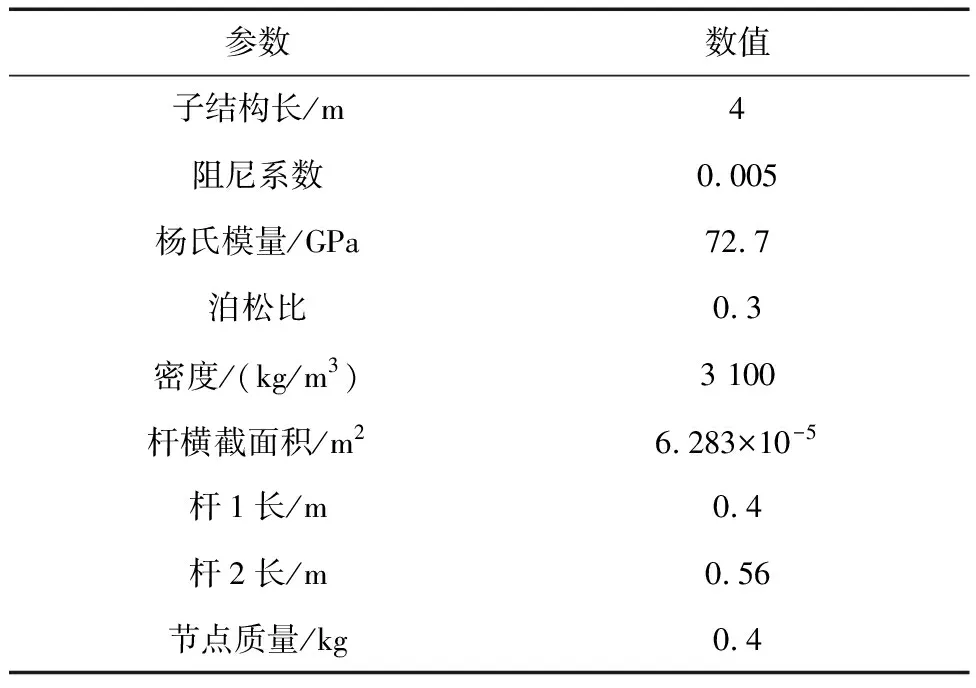
表1 桁架子结构的参数Tab.1 Parameters of the truss substructure

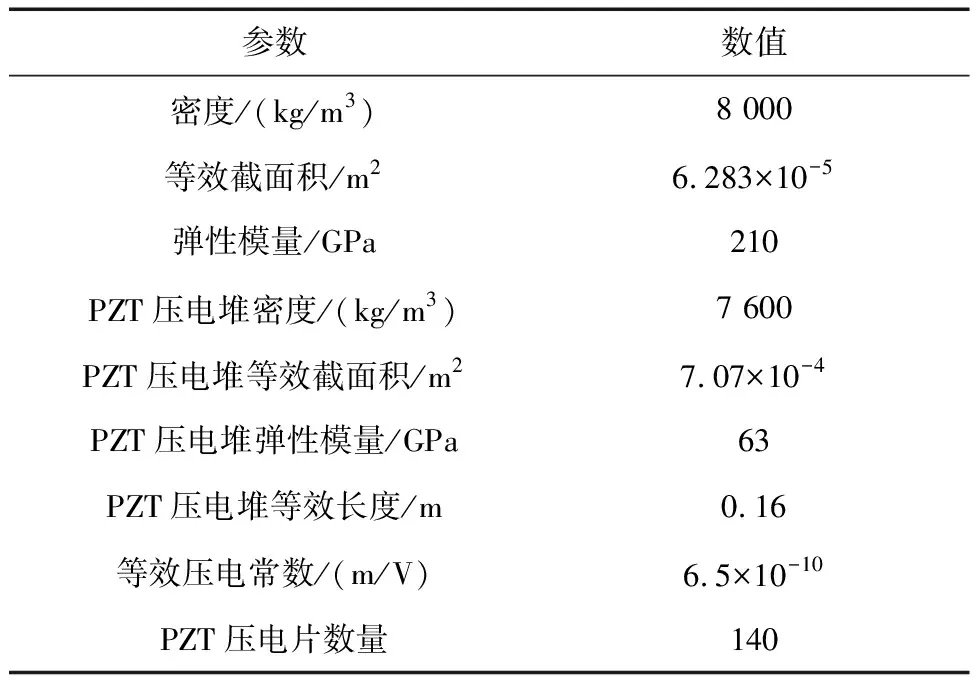
表2 压电主动杆参数Tab.2 Parameters of the piezoelectric active rod

图5给出了各个组装阶段配置3个作动器时考虑作动器对桁架结构动力学模型影响的适应度收敛曲线.

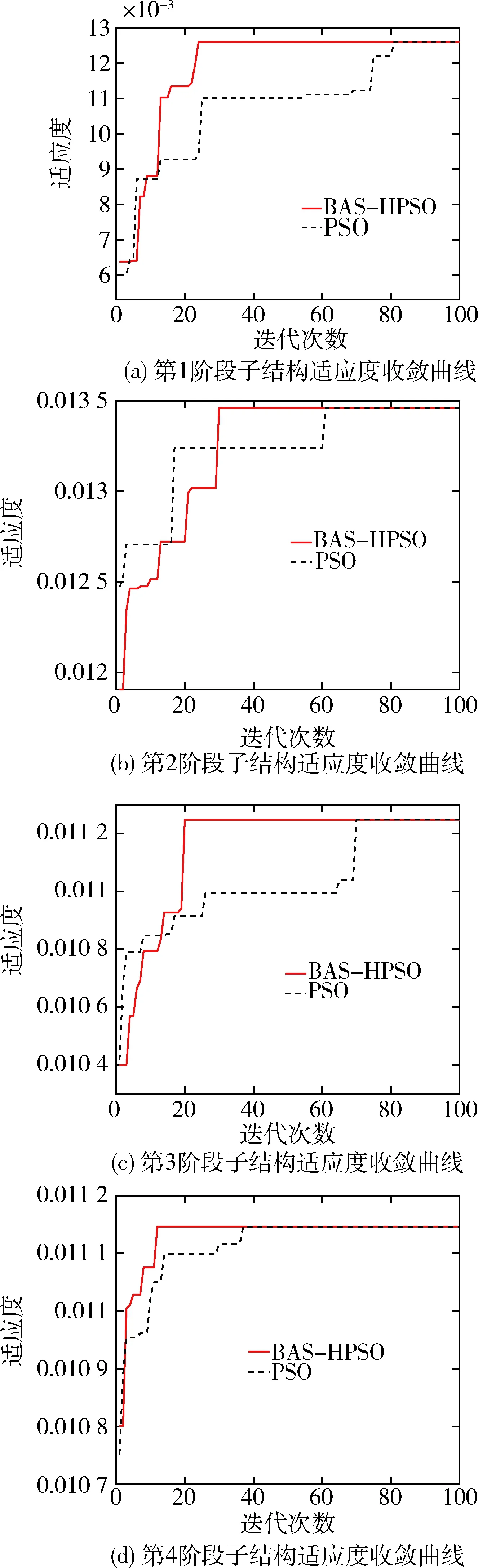
图5 配置3个作动器适应度收敛曲线Fig.5 The fitness convergence curves with 3 actuators

表3 配置3个作动器优化结果Tab.3 The results of optimization with 3 actuators

从图中的4个组装阶段可以看出,采用改进的混合粒子群算法进行的分布式优化配置均在30代以内完成收敛.在第1组装阶段采用改进的混合粒子群算法迭代了24次实现了收敛,而采用粒子群算法迭代了81次才达到收敛;第2组装阶段分别迭代了30次和61次实现了收敛;第3组装阶段分别迭代了20次和70次实现了收敛;第4组装阶段分别迭代了12次和37次实现了收敛.分析可知,相较于标准的粒子群算法,本文提出的改进的混合粒子群算法实现了桁架结构在轨组装阶段作动器的分布式优化配置,提高了收敛速度.运用改进的混合粒子群算法对在轨组装阶段桁架主动杆件进行分布式优化配置的结果如表3所示.

由于篇幅限制,仅给出前两个组装阶段压电主动杆的配置图如图6所示.

图6 配置压电作动器的位置图Fig.6 The position diagram of piezoelectric actuator

为了分析在轨组装阶段作动器分布式优化配置结果的优劣,采用2.2节提出的可控度准则式(14)对其进行评价,并与随机给定作动器位置的桁架结构进行对比,结果如表4所示.作动器未进行优化时即随机给定每个组装阶段桁架子结构作动器的位置.第1子结构为(1-5)、(7-11)、(25-29);第2子结构为(55-59)、(48-52)、(58-62);第3子结构为(85-89)、(86-91)、(95-100);第4子结构为(127-131)、(132-136)、(156-160).

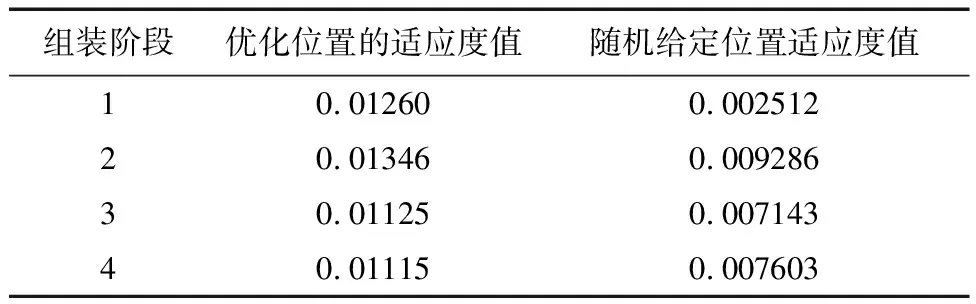
表4 配置3个作动器的适应度Tab.4 The fitness of optimization with 3 actuators

表4是采用改进的混合粒子群算法进行在轨组装阶段作动器分布式优化配置的结果评价,分别给出了优化后位置和随机位置的适应度值.由表4可以看出,第1次组装之后,经过位置配置优化后的适应度有极大的提升.4次组装之后,经过位置配置优化后的适应度提升46.7%.上述结果表明,通过对组装阶段作动器配置的分布式优化,实现了各个组装阶段作动器布局的最优配置,提高了系统可控度.此外,还通过穷举法计算了各组装阶段作动器可配置的所有位置的适应度值.结果表明通过穷举法得到的最优适应度值与通过算法优化得到配置位置的最优适应度值相同,说明了在轨组装阶段作动器分布式优化配置结果的准确性.

由文献[18-19]可知,对于一端固定的桁架结构而言,其一阶弯曲和扭转模态的应变能在根部处最大,因此压电主动杆应布置在桁架根部.桁架结构的二阶弯曲模态应变能在根部和中部两处存在极大值点,压电主动杆应布置在桁架根部和中部.桁架结构的三阶弯曲模态应变能在根部、中部和顶部3处存在极大值点.

由表5和图6可知,随着在轨组装的进行,桁架结构的固有频率和结构尺寸不断发生改变.结合各组装阶段的优化配置结果可知,对第1组装阶段桁架结构的3根压电主动杆的位置优化时,压电主动杆都布置于根部.对于第2组装阶段,桁架结构的尺寸增长了1倍,此时对第2个桁架子结构作动器的位置进行优化,作动器布置于第2组桁架结构的根部,也即第2组装阶段桁架结构的二阶弯曲模态的中部.同样的对于第3、4组装阶段的作动器配置时,优化后的作动器都布置在了靠近当前组装阶段桁架结构模态应变能较大的位置.由此证明了大型航天结构在轨组装阶段作动器分布式优化配置结果的有效性和准确性.

表5 各阶段的空间桁架固有频率Tab.5 Natural frequencies of space trusses at each stage

4 结 论

本文研究了在轨组装阶段大型航天结构作动器的布局优化问题,给出了在轨组装过程中大型航天结构作动器优化配置的设计思路.以桁架结构为研究对象,提出一种改进的混合粒子群算法,开展了优化配置的数值仿真研究.结果表明:1)本文提出的面向组装过程中的优化配置策略为解决在轨组装阶段的作动器优化配置问题提供了一种新的思路及方案;2)采用改进的混合粒子群算法可以实现桁架结构在轨组装过程中作动器的分布式最优配置,同时提高了优化收敛速度.