基于目标分配策略的空间碎片清除方案设计
杨保臻, 钱霙婧
北京工业大学, 北京 100124
0 引 言
近年来,人类探索宇宙奥秘的航天活动日益频繁,航天技术飞速发展的同时也带来新问题,空间碎片的个数不断增长,对在轨运行的航天器造成巨大的威胁,发生碰撞的风险大大增加.空间碎片在轨道上与航天器的平均相对运行速度大约10 km/s,在如此高的速度下毫米级的碎片撞击都有可能将在轨航天器的外壳击穿.1978年,美国宇航局科学家KESSLER[1]首次提出一项理论假设,认为当在近地轨道运转的航天器等的密度达到一定程度时,航天器相互碰撞后产生的碎片能够形成更多的新撞击,形成级联效应,此效应称为Kessler效应,意味着即使从此不再发射新的航天器进入太空,近地轨道同样将覆盖危险的太空垃圾.由于失去能够安全运行的轨道,在之后的数百年内太空探索和人造卫星的运用将变得无法实施.因此,主动清除空间碎片是解除空间碎片危机的根本方法.
空间碎片的主动清除目前尚处于研究阶段[2],设想大致可分为接触式[3](通过捕获机构进行抓捕碎片)和非接触式[4](强激光束照射碎片降低碎片轨道、静电力增阻对碎片充电使其减速离轨).其中,非接触式主动清除方法虽然可以避免与空间碎片产生直接接触,但是同时也增加了相应的难度和不可控制性.接触式捕获离轨的清除方式不但可以用来执行其他持续清除碎片任务,同时还可以适用较广的轨道高度范围以及碎片清除范围[5-6].
在执行空间碎片清除任务时,首先应考虑数量众多的空间碎片的清除对象选择.作为非合作目标的空间碎片,通过掌握其分布的总体情况与碎片的物理特性确定清除对象的大致选择范围[7-8].对于一对多的碎片除任务包括清除碎片数量、清除序列的设定等问题,于锡铮等[9]研究了单次任务中在多脉冲推力作用下轨道机动清除12颗集中分布的碎片的方法.BONNAL等[10]研究了单个飞行器清除多碎片的问题,并利用权重系数法求解了同时考虑燃耗和时间的单目标优化问题.BÉREND和CERF等[11-12]利用分支定界法研究了多碎片清除任务序列优化和轨道转移优化问题.MISSEL等[13]采用遗传算法求解系统中的碎片清除任务规划问题.先前的文献研究从主动清除角度考虑了单个飞行器一对多持续清除碎片任务,且需清除的多块碎片有一定的位置分布要求,无法短时间内协同清除大量威胁在轨卫星或者飞行器的多块空间碎片.
不同于以往使用单个飞行器执行任务,本文以利用卫星星座构型中多颗在轨卫星同时释放带有抓捕机构的飞行器执行碎片清除任务为背景,针对碎片对象选择及清除序列采用单转移飞行器进行一对多碎片清除任务.以燃料消耗为指标,利用降低碎片分布密度的DBSACN聚类算法对初步选取的空间碎片群进行碎片分类,并采用基于匈牙利算法的任务分配选择具体在轨卫星下放飞行器执行相应碎片持续清除任务.相对于以往研究可实现快速降低相应区域碎片分布密度,保障在轨航天器的安全.
1 问题描述
1.1 空间飞行器与卫星运动模型
惯性坐标系是指相对于宇宙的其他部分而言没有加速度和转动的坐标系.如图1所示,其原点位于地球质心Oe处,OeX轴在赤道平面内沿着地心Oe与平春分点的连线,指向平春分点;OeZ轴沿地球自转轴方向从地心指向北极点.OeY轴与OeX、OeZ轴垂直并满足右手定则.

图1 地心惯性坐标系(ECI)Fig.1 Geocentric inertial coordinate system (ECI)
卫星执行碎片清除任务时释放的空间飞行器在飞行过程中受到地球的引力,二体动力学方程[14]在地心惯性坐标系下表示为
(1)
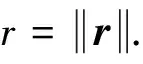
1.2 空间飞行器交会制导方法
空间飞行器交会对接过程一般分为4个阶段:远距离导引段、近距离导引段、平移靠拢段和对接段[15-16].本文重点在于多碎片清除任务设计,制导方法采用Lambert制导来估算远距离导引段算法中卫星释放空间飞行器捕捉碎片以及空间飞行器持续清除碎片所需的燃料消耗.
空间飞行器在大气层外飞行受到地球引力作用与其构成二体模型.二体运动相对惯性空间的运动方程是二阶常微分方程[17].具体到当前的二体问题,若初始位置矢量和速度矢量已知,可以通过二体运动方程计算空间飞行器相应时间的位置和速度.此问题称为初值问题.若初始时刻和终点的位置矢量已知,则求得空间飞行器初始位置处的速度矢量.此问题称为两点边值问题.
Lambert问题是在固定时间约束下的两点边值问题,是航天器轨道动力学的经典和基本问题.通过求解Lambert问题计算卫星释放的带有捕获机构的飞行器飞行到目标碎片附近所需的速度增量,如图2所示,仅考虑中心天体C的引力,飞行器Lambert转移轨道为从起始位置P1点飞行到终点位置P2点,因此相对于中心天体C,确定起始位置矢量与终点位置矢量,飞行时间为Δt.起点P1的地心距为r1,终点P2的地心距为r2,飞行路径所对应的地心角为θ.此两点轨道转移所需要的时间Δt仅与始末位置的几何构型以及轨道半长径有关,而与其他轨道参数无关,通过给出初始时刻与终点时刻的位置矢量r1、r2、转移轨道的角度θ、转移时间Δt并通过Lambert求解算法则可得到空间飞行器变轨机动后初始时刻与终点时刻的速度矢量[18].

图2 Lambert转移轨道几何构型Fig.2 Lambert transfer orbital geometry
2 目标碎片选择与分类
2.1 目标碎片初步选择
地球周围的空间碎片不计其数,按照尺寸大小可分为3大类:(1)大型空间碎片:直径超过10 cm,占据碎片总质量的99%;(2)中型碎片:直径在1~10 cm之间,也成为了危险碎片;(3)小型碎片:直径小于1 cm,数量巨大且难以探测[19-20].空间碎片的分布密集区域主要集中在3部分:500~2 000 km的LEO区域、20 000 km的中轨区域以及36 000 km的GEO区域.在空间碎片分布的3大密集区域中,LEO相对运动速度较大并且运动方向存在交叉,碰撞事件的发生概率较高,因此本文选定LEO区域的大型碎片与火箭箭体为初步清除目标.
根据Space-Track网站公布的数据,如图3~5所示,LEO区域中在轨的中小型碎片分别有11 326个、1 643个,在轨大型碎片有116个,在轨火箭箭体934个.中小型碎片的绝大部分是由于大型碎片或者火箭箭体碰撞导致,为抑制Kessler效应,应优先考虑清除箭体等大型碎片,并且箭体等结构坚固,对捕获机构要求不高.根据图5中空间碎片分布,大型空间碎片和火箭箭体在轨道倾角97°~100°间分布较为密集.考虑到减少燃料消耗,除减少较大倾角的轨道机动外,还应选择升交点赤经变动在一定范围内的碎片.
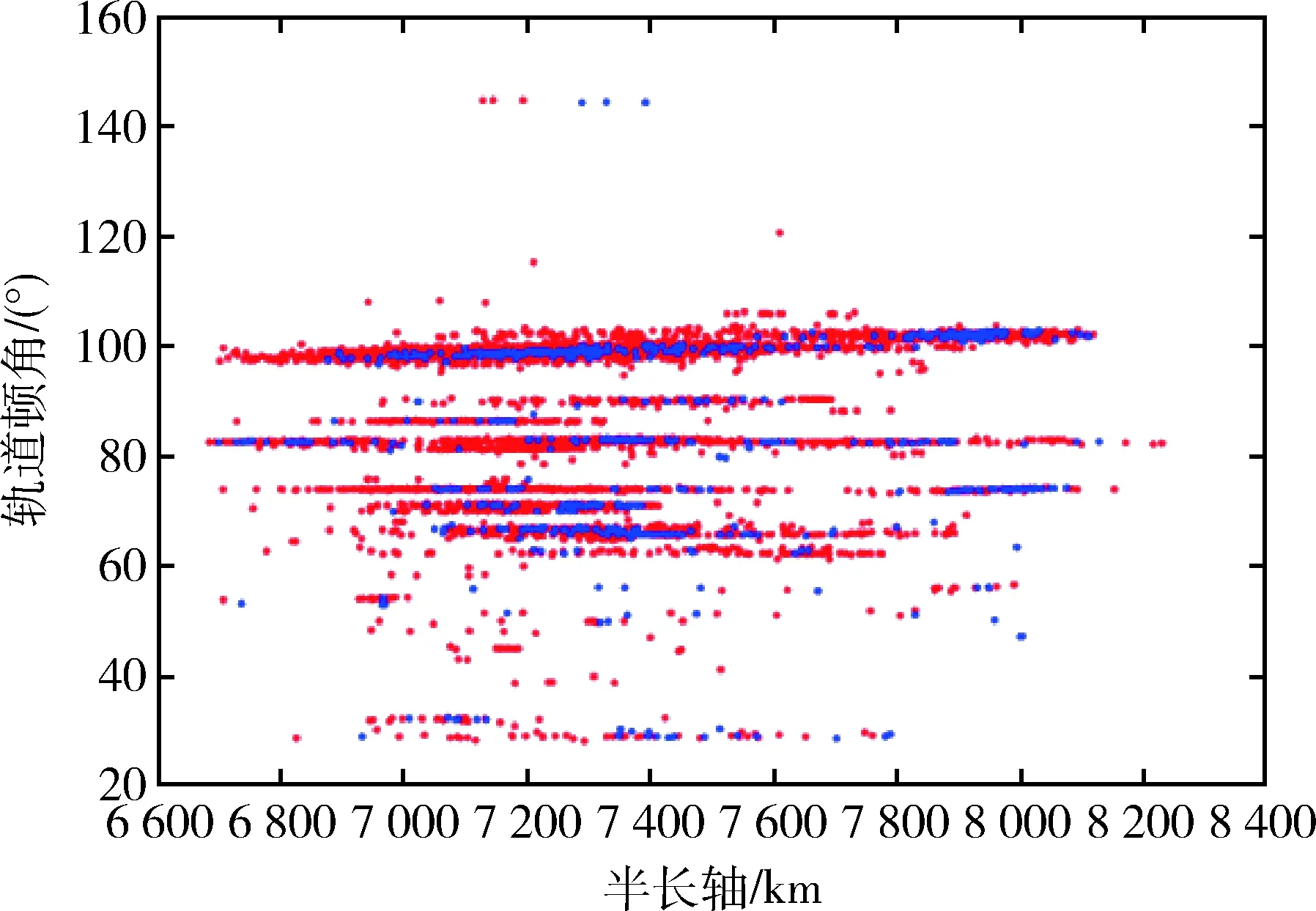
图3 LEO在轨中小型碎片Fig.3 Small and medium fragments in LEO
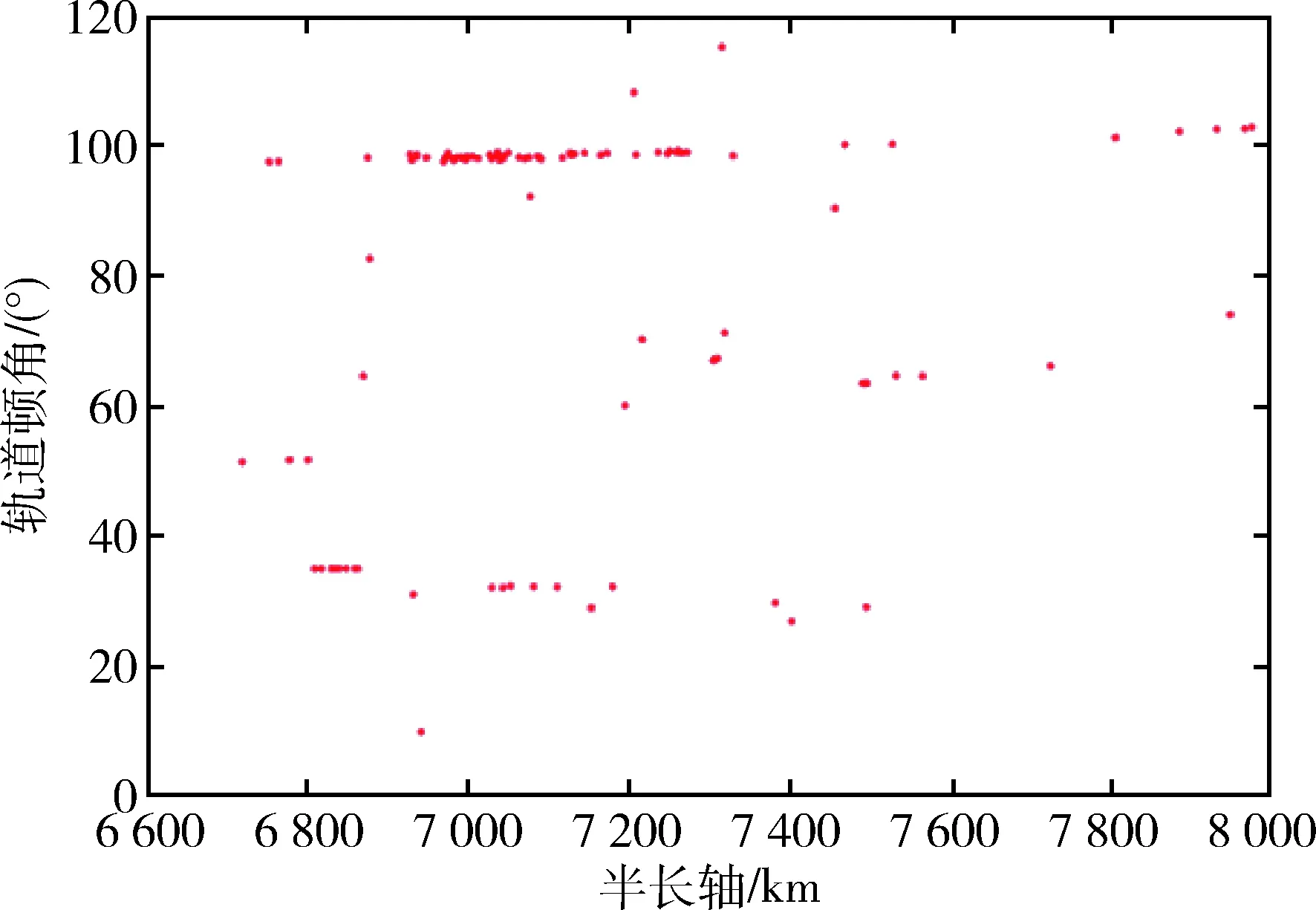
图4 LEO在轨大型碎片Fig.4 Large debris in LEO
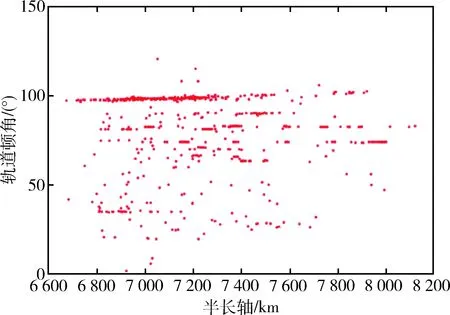
图5 LEO在轨火箭箭体Fig.5 Rocket bodies in LEO
2.2 基于密度的聚类算法-DBSCAN算法
通过确定部分轨道要素与碎片大小的方法已经初步选定一组目标碎片,希望通过空间飞行器实现一对多的碎片清除任务要根据碎片特性进一步分类.聚类是无监督学习任务之一,聚类是数据挖掘中的概念[21],就是按照某个特定标准或特征(如距离)把一个数据集分割成不同的类或簇,需要通过分析将数据对象中潜在的特征信息发掘并设定合适的评判标准,使得同一个簇内的数据对象的相似性尽可能大,同时不在同一个簇中的数据对象的差异性也尽可能大.聚类后同一类的数据尽可能聚集到一起,不同类数据尽量分离.DBSCAN算法[22]的聚类定义很简单:由密度可达关系导出的最大密度相连的样本集合,即为本文最终聚类的一个类别,或者说一个簇.
DBSCAN是通过一组邻域来描述样本集的紧密程度,参数(∈,Minpts)用来描述邻域的样本分布紧密程度.其中,用∈描述某一样本的邻域距离阈值,Minpts描述某一样本的距离为∈的邻域中样本个数的阈值,样本集记为D=(x1,x2,…,xm),DBSCAN算法的关键性定义如下:
(1)∈-邻域:对于样本集中任一样本xj∈D,其∈-邻域包含样本集D中与xj的距离不大于∈的子样本集,即N∈(xj)∩{xi∈D|distance(xi,xj)≤∈},这个子样本集的个数记为|N∈(xj)|.
(2)核心对象:对于任一样本xj∈D,如果其∈-邻域对应的N∈(xj)至少包含Minpts个样本,即如果|N∈(xj)|≥Minpts,则xj是核心对象.
(3)密度直达:若xi位于xj的∈-邻域中,且xi是核心对象,则称xi由xj密度直达.但是反之不一定正确,即此时并不能确定xj由xi密度直达, 除非且xi也是核心对象.
(4)密度可达:对于xi和xj,如果存在样本序列p1,p2,…,pT,满足p1=xi,pT=xj,且pt+1由pt密度直达,则称xj由xi密度可达.即密度可达满足传递性.
通过DBSCAN算法划分的簇中有一个或者多个核心对象.当某个簇里只有一个核心对象时,则簇里其他的非核心对象样本都在此核心对象的∈-邻域里;当某个簇里有多个核心对象,则簇里任意一个核心对象的∈-邻域中必定有一个其他的核心对象从而实现两个核心对象间的密度可达.这些核心对象的∈-邻域里所有的样本的集合组成一个聚类簇.
根据初步选择出的一组目标碎片,将其所在位置相互间转移所需的速度增量集合设定为一样本集,∈-邻域描述为空间飞行器从某碎片到另一碎片所需的燃料消耗阈值,Minpts描述为到达某一碎片后,周围存在燃料消耗允许范围内潜在的清除碎片数量阈值.
如图6所示,Minpts=5,红色的点都是核心对象,因为其∈-邻域至少有5个样本.黑色的样本是非核心对象.所有核心对象密度直达的样本在以红色核心对象为中心的超球体内,若不在超球体内,则不能密度直达.用绿色箭头连起来的核心对象组成了密度可达的样本序列.在上述密度可达的样本序列的∈-邻域内所有样本构成一个簇.
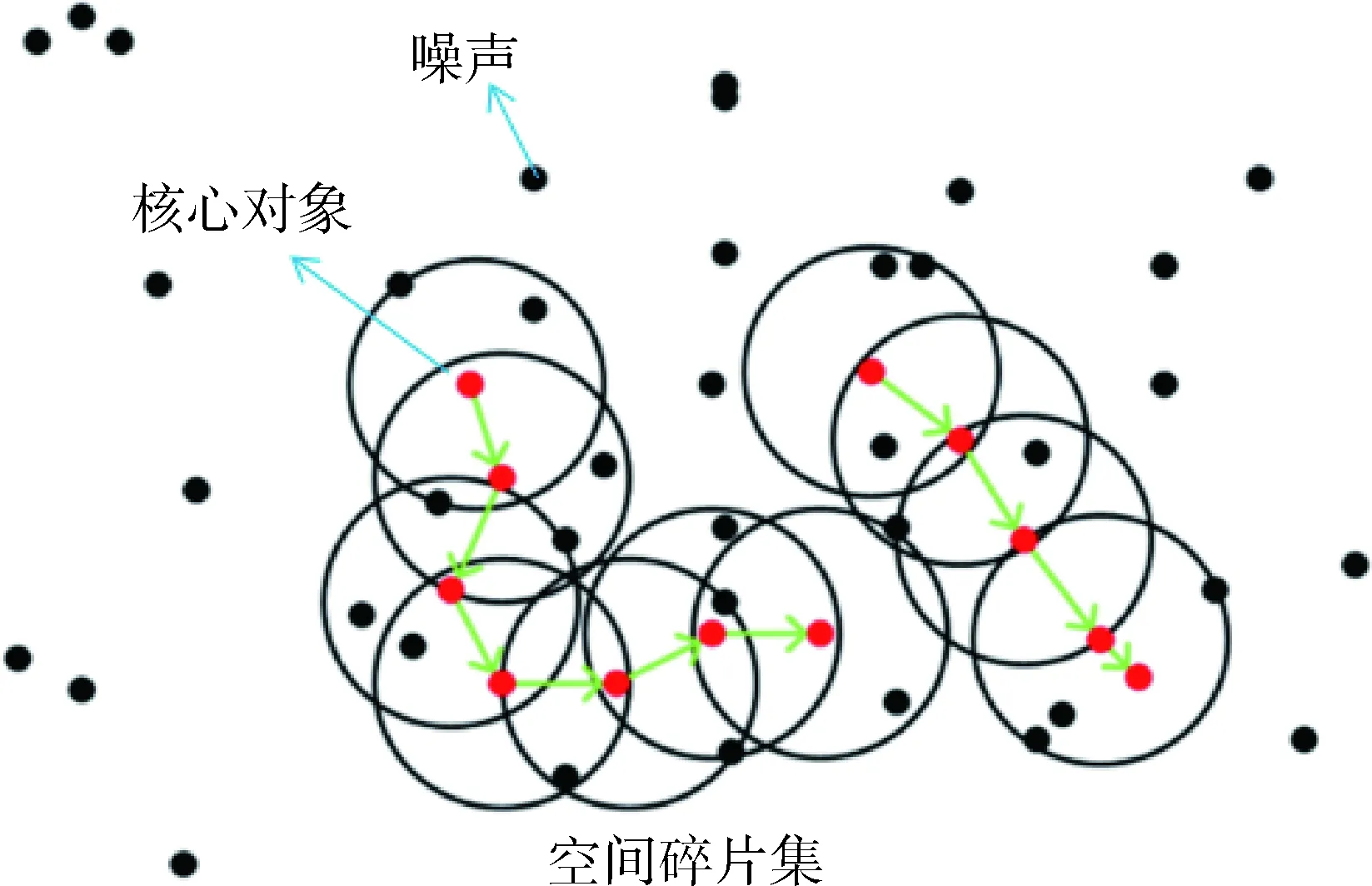
图6 DBSACN分类概念说明图Fig.6 DBSACN classification concept diagram
针对碎片清除任务,碎片分类算法设计如下:

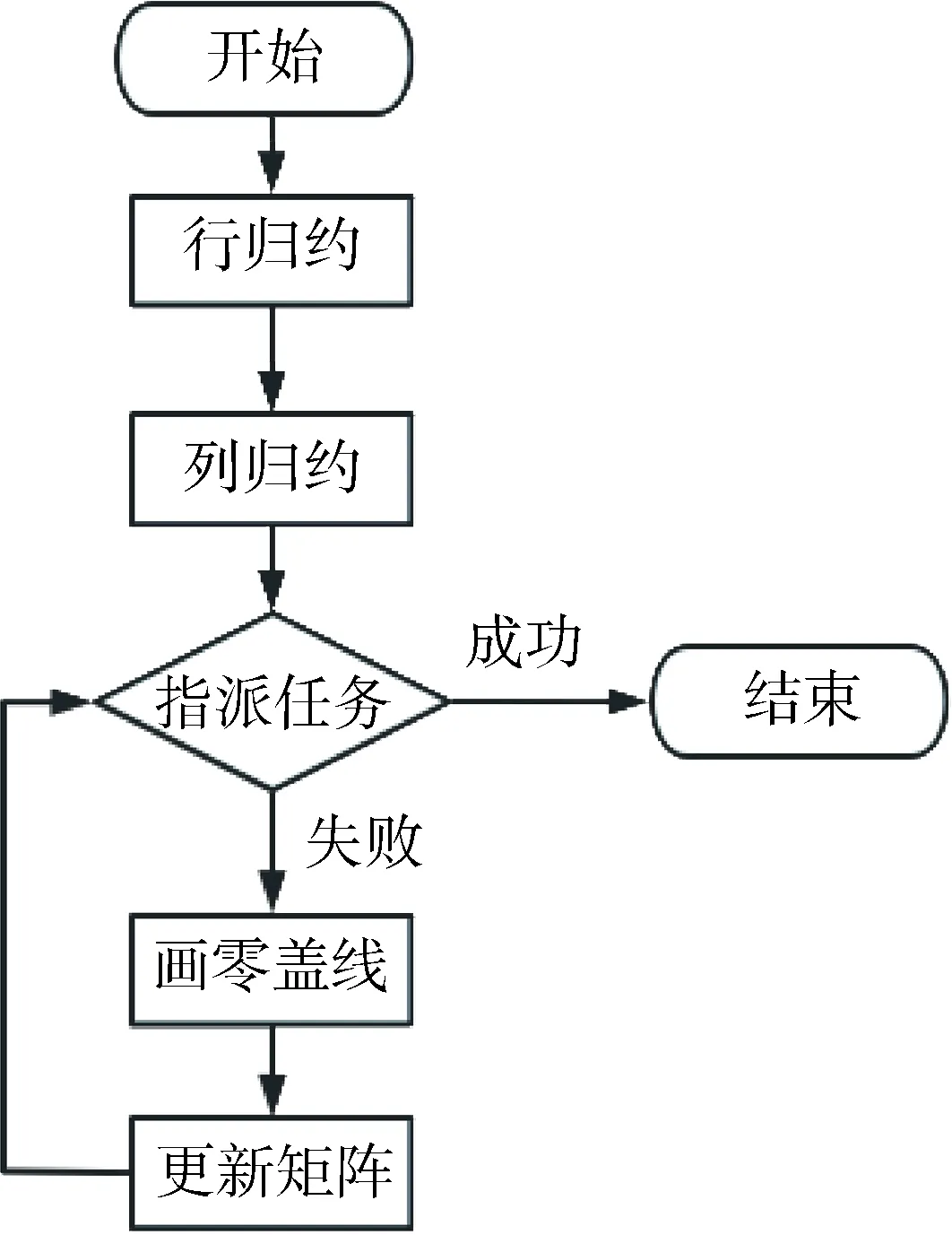
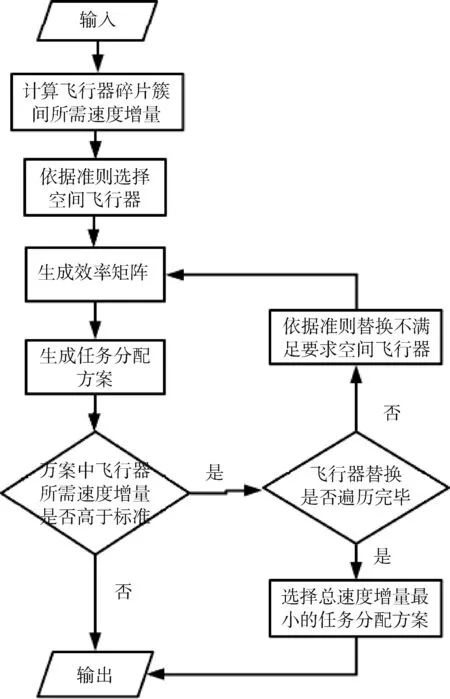
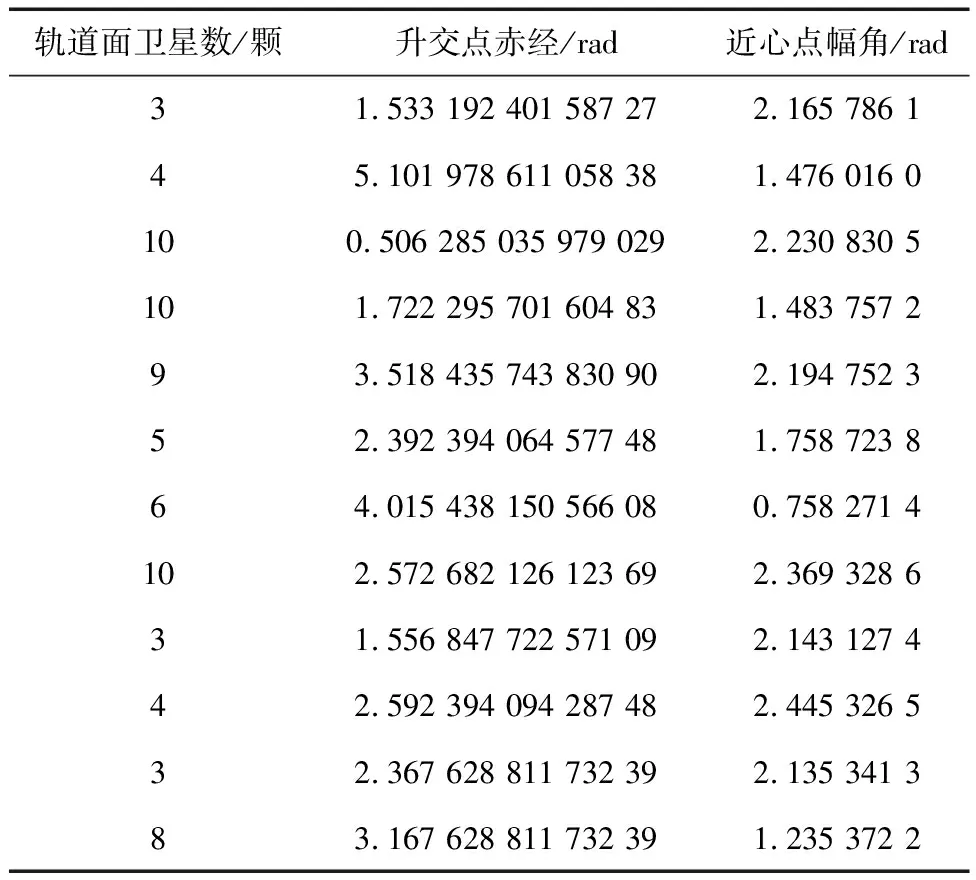
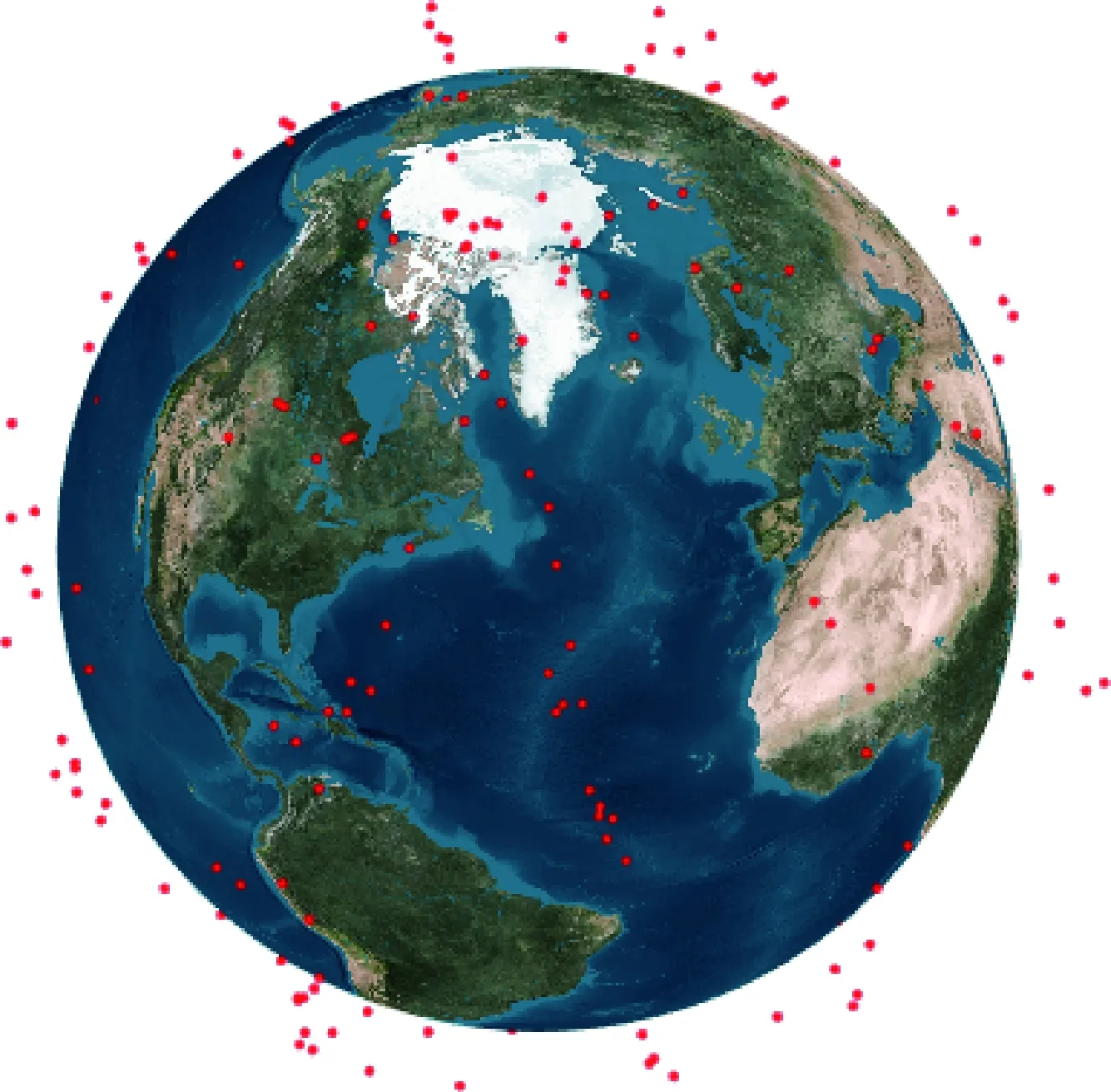
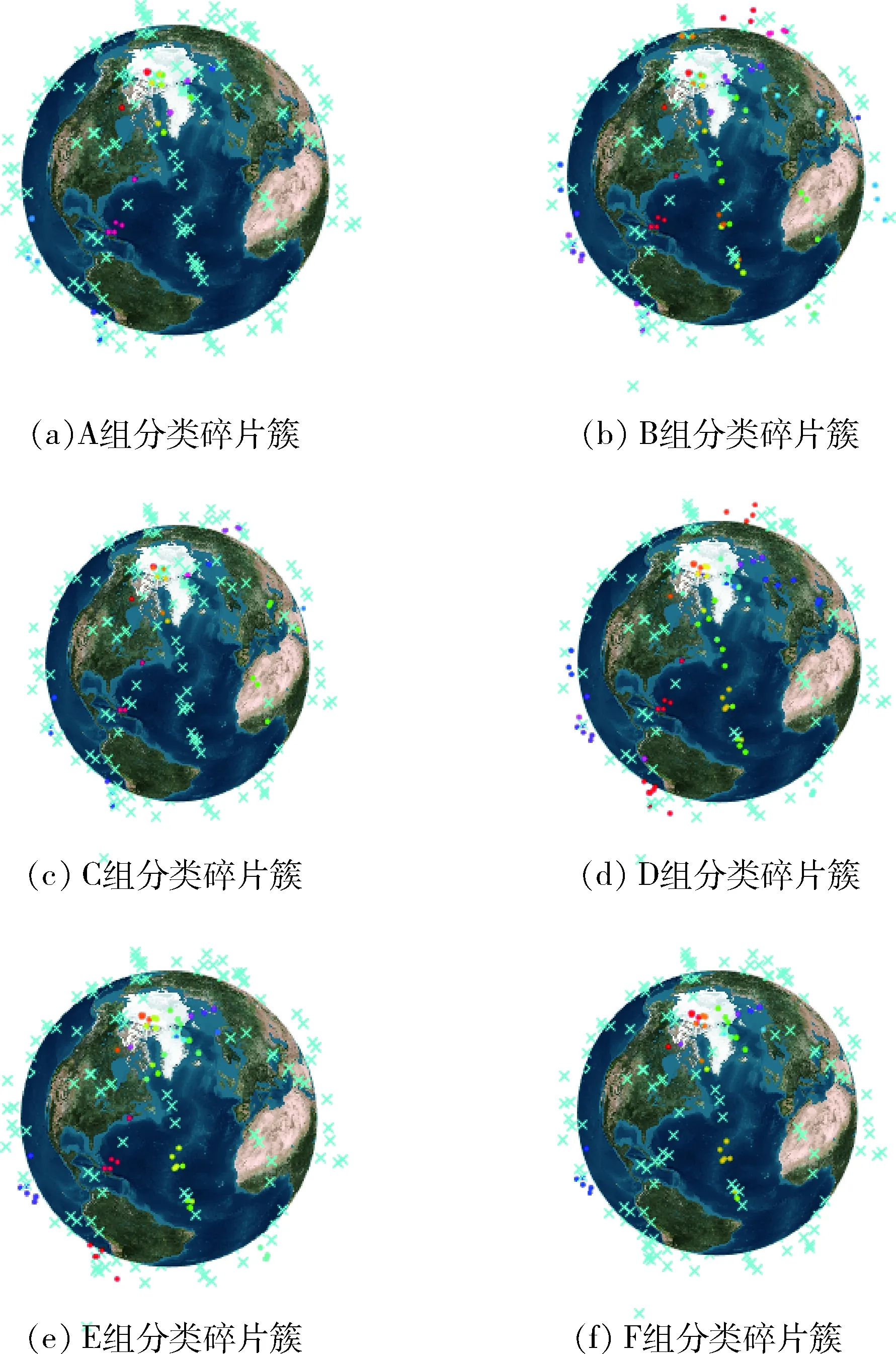
算法1:碎片分类算法输入:样本集D,邻域参数∈,样本距离度量Minpts输出:碎片簇向量C与噪声Is与核心对象Vcore1 由D生成n×n成本矩阵M,n维全零向量C、全逻辑零向量Vs、Is, Q=02 for i =1 to n do3 if Vs(i)为0 then4 将Vs(i)改为逻辑1,寻找M中当前行满足∈要求的对象Neighbors5 if Neighbors数量 输入:样本集D=(x1,x2,…,xm),邻域参数(∈,Minpts),样本距离度量方式(碎片间转移所需燃料消耗) 输出:碎片样本集划分出的簇C={C1,C2,…,Ck}与噪声 1)初始化核心对象集合Ωcur=φ,初始化聚类簇数,初始化未访问碎片样本集合Γ=D,簇划分C=φ; 2)对于j=1,2,…,m,按下述步骤找出所有核心对象: a)通过距离度量方式,找到样本xj的∈-邻域子样本集N∈(xj); b)若子样本集中样本个数满足|N∈(xj)|≥Minpts,将样本xj加入核心对象样本集合:Ω=Ω∪{xj}. 3)若核心对象集合Ω=φ,跳出步骤2,计算完成,否则转入步骤4; 4)在核心对象集合中,任选一核心对象o,初始化当前簇核心对象序列Ωcur={o}, 初始化类别序号k=k+1,初始化当前簇样本集合Ck={o},更新未访问样本集合Γ=Γ-{o}; 5)如果当前簇核心对象序列Ωcur=φ,则当前聚类簇Ck生成完毕,更新簇划分C={C1,C2,…,Ck}更新核心对象集合Ω=Ω-Ck,转入步骤3.否则更新核心对象集合Ω=Ω-Ck; 6)在当前簇核心对象序列Ωcur中选取一核心对象o′,通过邻域距离阈值∈找出所有的∈邻域子样本集N∈(o’),令Δ=N∈(o’)∩Γ,更新当前簇样本集合Ck=Ck∪Δ,更新未访问样本集合Γ=Γ-Δ,更新Ωcur=Ωcur∪(Δ∩Ω)-o’,返回步骤5. KUHN提出的匈牙利算法(Hungarian algorithm)是一种关于指派问题的求解方法,其引用了匈牙利数学家康尼格的一个关于矩阵中独立零元素个数的定理:矩阵中独立零元素的个数等于能够覆盖所有零元素的最少直线数[23-24].结合本文研究,矩阵中的不同行和列确定的位置元素对应不同空间飞行器去抓捕不同碎片所需的燃料消耗.算法基本思想是修改效率矩阵的行或列,使得每行或每列中至少有个零元素,通过修改直至在不同行列中最少存在一个零元素,得到与所有零元素位置相对应的任务分配方案并且为效率矩阵中的最优分配,此方案使任务花费的成本最小. 假设一颗卫星可以释放n个空间飞行器,将所有卫星能够释放的空间飞行器编入执行任务集,则卫星释放空间飞行器清除碎片指派问题模型. (1)决策变量 若xij=1,即指派第i个空间飞行器到达第j碎片簇的第一个核心对象附近并持续清除碎片簇中相应核心对象.若xij=0,即不指派第i个空间飞行器到达第j碎片簇的第一个核心对象附近并持续清除碎片簇中相应核心对象. (2)目标函数 (2) 式中,Cij为第i个空间飞行器到达第j碎片簇的第一个核心对象附近所需的燃料消耗. (3)约束条件 a)xij只能为0或1; 求解指派任务步骤流程如图7所示,其中关键步骤定义如下: 图7 求解指派问题的匈牙利算法流程Fig.7 Hungarian algorithm flow for solving assignment problem (1)行列归约.寻找每行和每列中最小元素,分别从每行和每列中减去这个最小元素. (2)指派任务(确定独立零元素).圈零法:依次寻找只有一个零元素的行或列并圈出,并划去该零元素所在的列或行中其他零元素,此时可能出现3种情况: a)每行都有独立零元素,个数满足m=n时得到最优解,跳出所有计算步骤,算法完成. b)存在未被标记的零元素,并且其所在行列中未被标记的零元素均至少有两个,可得到最优解.此时从剩余零元素最少的行或列开始,选零元素画圈,然后划掉同行同列的其它零元素,反复进行,直到所有零元素均被圈出或划掉为止. c)不存在未被标记过的零元素,但圈零个数m (3)画盖零线.利用最少的水平线和垂直线覆盖所有的零元素: a)对效率矩阵中所有不含圈零元素的行打√; b)对打√的行中所有零元素所在列打√; c)对所有打√的列中圈零元素所在行打√; d)重复上述第b)和c)步,直到不能继续为止; e)对未打√的每一行画一直线,对已打√的每一列画一纵线. (4)更新矩阵.跟经过画盖零线后的矩阵进一步交换增加零元素,在未被直线覆盖过的元素中找出最小元素,将打√行的各元素减去这个最小元素,同时将打√列的各元素加上这个最小元素. 每颗卫星可以释放n个空间飞行器,将所有卫星能够释放的空间飞行器编入执行任务集与碎片簇位置速度数据作为输入,整体任务分配流程如图8所示. 图8 整体任务分配实现流程Fig.8 Overall task allocation implementation process 飞行器挑选准则:通过空间飞行器任务集与计算空间飞行器到达碎片簇间所需速度增量生成速度增量集,依据速度增量集将所有空间飞行器到达相应碎片簇首个核心对象附近所需速度增量按照由小到大顺序排列,后根据所需执行任务的空间飞行器数量首先选择到达相应碎片簇首个核心对象附近所需速度增量的飞行器,即速度增量集排列后的第一行数据对应的空间飞行器编号,若数量没有达到执行任务的飞行器数量要求,则继续从下一行选取直到满足数量要求.值得注意的是,流程中替换执行任务的飞行器时从先前挑选终止处继续进行. 考虑到清除LEO附近的空间碎片,算例采用基于Walker星座随机生成LEO附近容易受此处碎片威胁的一星座构型中的在轨卫星释放飞行器执行碎片清除任务,其中飞行器由抓捕手臂和平台两部分构成,平台包括结构、通讯、制导等系统构成,星座卫星具体轨道数据如表1所示,卫星轨道半长轴为7 575.3 km,偏心率为0.042 86,轨道倾角为1.435 rad. 表1 卫星星座轨道要素数据Tab.1 Orbit element data of satellite constellation 根据先前的空间碎片分析对在轨碎片进行初步选择,并选择升交点赤经差值在20°范围的多组碎片,如图9所示共计282颗. 图9 目标碎片分布Fig.9 Target fragments distribution 如图10所示,DBSCAN算法中邻域参数(∈,Minpts)在任务背景下的具体表现为(速度增量限制、超球体内碎片密度),6组任务邻域参数分别为(2 km/s,4块)、(2 km/s,3块)、(1.5 km/s,3块)、(3 km/s,4块)、(3 km/s,5块)和(3 km/s,6块),飞行器在碎片间转移时间设定为100 s,以此进行分类,分别选出45块、118块、58块、139块、96块和67块碎片,分别分为14个、41个、22个、45个、30个和22个碎片簇. 图10 目标碎片分类Fig.10 Target fragments classification 图10(a)~(f)中蓝色叉号为噪声,彩色各点不同颜色代表不同的碎片簇,同一颜色为同一碎片簇.图11(a)~(f)中为各个碎片簇中的核心对象数量情况. 图11 各碎片簇中核心对象数量Fig.11 Number of core objects in each debris cluster 假设每颗卫星最多能释放3个空间飞行器,6次整体碎片清除任务如图12(a)~(f)所示,黄色为执行任务的卫星释放空间飞行器,红色为碎片簇第一个核心对象. 图12 整体碎片清除任务Fig.12 Overall fragments removal task 假设每颗卫星最多能释放3个空间飞行器,空间飞行器与碎片交会制导时间为100 s,对速度增量的限制在10 km/s,6次整体碎片清除任务中具体所需速度增量情况与任务分配情况如图13(a)~(f)所示,图中标记为碎片编号. 图13 碎片清除任务分配Fig.13 Debris clearing task allocation 仿真结果可知,在碎片分类中,参数约束较小的B组与D组选取了更多碎片进行分类,分成了40个以上的碎片簇,并且有接近10个碎片簇中有多个核心对象;有参数约束较大的A组选取了较少碎片分类,分成了20个以下的碎片簇,并且绝大部分碎片簇中只包含一个核心对象.6次整体碎片清除任务星座构型的75颗卫星分别采用了其中10颗、27颗、17颗、27颗、20颗和14颗卫星执行各类碎片簇的清除任务,其中包含有些卫星被多次匹配,释放1~3个空间飞行器执行不同碎片簇的清除任务,并保证了交会制导所需速度增量大部分保持在6 km/s以下,DBSACN聚类算法随着超球体中碎片密度的降低与所需最大燃料消耗要求的提高,更容易从目标碎片中分出多颗碎片执行任务,并且碎片簇数量越多,分类越散,许多碎片簇中只包含一个核心对象,没有进行一对多的碎片清除任务. 本文通过对空间碎片分布情况进行分析,初步选择一组目标碎片,并利用碎片清除任务实际情况根据碎片间转移所需燃料消耗及碎片分布密度对所选碎片进行不同种类的有效区分,划分不同的碎片簇.根据求解指派问题的匈牙利算法通过星座中在轨卫星设计整体碎片清除分配任务,仿真结果表明通过星座构型中10~30颗在轨卫星可以短时间内在较小燃料消耗成本下完成任务.3 基于匈牙利算法的清除碎片任务分配策略
3.1 求解指派问题的匈牙利算法
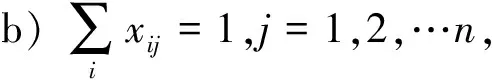
3.2 整体清除碎片任务分配
4 仿真算例



5 结 论

