柔性失效卫星能量耗散与运动演化特性研究

盛 超, 宋 超, 沈红新

1. 宇航动力学国家重点实验室, 西安 710043 2. 西安卫星测控中心, 西安 710043

0 引 言

随着人类科技水平的不断进步,世界各国对太空的探索也愈发频繁与深入.在轨航天器的种类、数量不断提升,航天任务逐渐呈现出复杂化、精细化的发展趋势,航天器在遥感成像、通信中继、深空探测与授时定位等领域起到了难以取代的作用,但太空环境具有高真空、强辐射与温度变化剧烈等特性[1],这对航天器上仪器设备的正常工作提出了严峻的挑战.合理利用并及时维护航天器,具有十分重要的科学价值与经济效益.

20世纪以来,全世界范围内卫星及其应用产业发展十分迅速.据统计,2022年世界航天共实施186次发射任务,发射航天器2 505个,均创历史新高.随着在轨航天器数量的不断增加以及空间任务的不断复杂,在轨卫星故障事件的数量与复杂度不断增长[2].为尽快恢复失效卫星功能,一方面需要地面卫星测控部门分析预测卫星的姿轨位置,在合适时机发送遥控指令以重启卫星,例如2006年我国某型号卫星在入轨后的太阳帆板展开阶段突然信号中断,专家分析后认为该事件起因是帆板故障导致卫星断电,后经专业技术人员推测断电时刻并预估卫星运动状态,利用卫星帆板对日时可短暂接受地面遥控指令的时机,调整帆板姿态使其能持续供电,最终成功使卫星恢复正常[3].另一方面,可利用空间机械臂实施在轨维修、捕获与回收等操作,避免失效卫星长期占用轨道位置,影响其他卫星正常工作,例如欧空局针对其失效卫星Envisat启动了e.Deorbit项目[4],拟采用新型机械臂、飞网、鱼叉等机构对Envisat进行捕获并实施离轨处置[5],但目前仍未有实质性的操作进展.

为快速有效开展失效卫星的地面抢救与在轨维护任务,需要准确把握卫星的运动规律并预测卫星姿轨状态,从而在恰当时机发送遥控指令或实施捕获操作[6].蔡立锋等[7]对卫星受到重力梯度力矩作用下的自旋运动,特别是自旋轴和章动角的变化特性进行了分析,能够对近地卫星姿态失控后的姿态确定和运动预测提供参考.EFIMOV等[8]针对太阳同步轨道上卫星受到电涡流阻尼力矩的情况,根据刚体运动的Hamilton函数建立了航天器运动的精确模型,分析了航天器姿态与角动量矢量的演化情况.COCHRAN[9]采用一种基于Lie代数生成近似正则变换的一般摄动方法,分析了重力梯度力矩作用下航天器长期自旋运动的演化情况.刘延柱[10]基于Serret-Andoyer变量建立了刚体的定点运动方程,并分析了受微弱力矩作用的刚体或高速旋转刚体的运动特征.

图1 近年来在轨卫星故障情况统计Fig.1 Statistics of satellite failures in orbit in recent years

上述研究均针对外部环境摄动作用下航天器的运动演化过程展开研究,随着空间任务的不断深入与复杂,航天器逐渐向着大型化、复杂化和柔性化的方向发展,太阳帆板、机械臂与天线等大型柔性附件得到了广泛的应用[13],携带这类柔性附件航天器的姿轨运动与弹性振动之间存在着复杂的耦合关系[12],并且柔性附件的弹性振动会持续耗散航天器的能量,相比于外部空间环境造成的扰动[15],这种内部因素对航天器运动演化的影响更为显著.以携带大型太阳帆板的典型失效卫星Envisat为例,其观测数据表明,截至2013年5月份,Envisat的角速度曾有一段迅速增加的时期,目前学界对这一现象的成因仍无统一解释,随后Envisat的角速度呈缓慢降低趋势,研究表明这是由于卫星电涡流与地磁场相互作用,不断损耗卫星能量所致.目前学界关于Envisat的自旋运动趋势以及主要影响因素虽达成一定共识,但仍未有能够准确描述其运动演化规律的数学模型[16],这进一步提升了Envisat后续处理任务的设计难度.

本文以柔性失效卫星的抢救与维修任务设计需求为牵引,针对一类携带大型柔性附件的失效航天器,分析其能量损耗过程与对应的运动演化规律,首先基于拉格朗日方程建立柔性航天器的姿态-振动耦合动力学模型,然后根据能量耗散规律分析柔性航天器不同自旋状态的稳定性,最后分析了卫星初始角速度、柔性附件的安装位置、柔性附件的初始振动状态、柔性结构与材料特性等因素对能量耗散速率的影响,并从能量耗散规律的角度分析了航天器的运动演化趋势.

1 携带柔性附件航天器的动力学建模

首先对航天器动力学模型推导过程中使用的坐标系进行说明:

(1)中心体坐标系fb(ObXbYbZb):原点在中心体质心,坐标轴为中心体惯量主轴;

(2)柔性附件坐标系ff(OfXfYfZf):原点在附件与中心体的连接点,坐标轴固连于附件上;

(3)航天器坐标系fs(OsXsYsZs):原点在航天器质心,坐标轴为航天器惯量主轴.

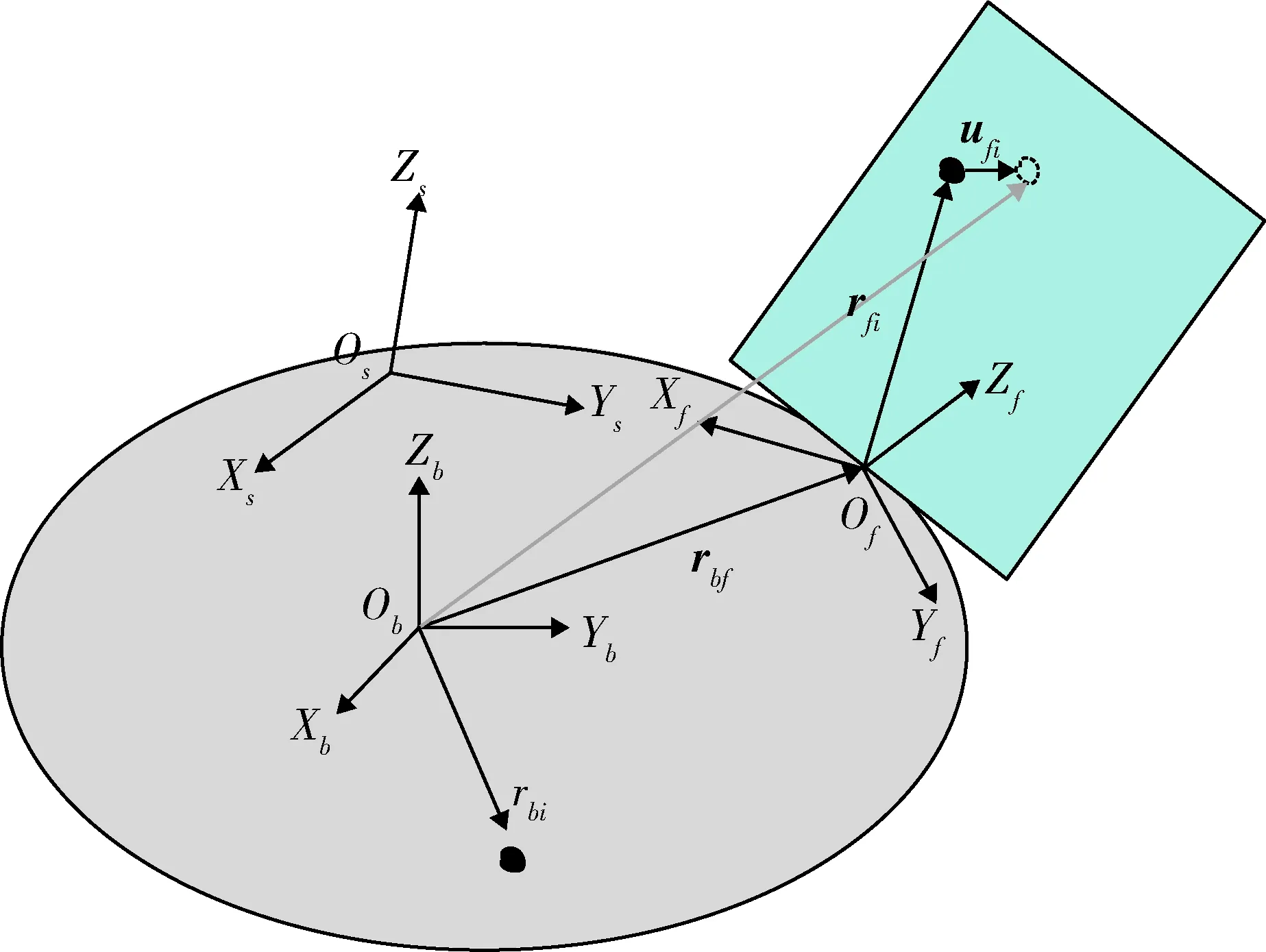
图2 航天器动力学模型示意图Fig.2 Schematic diagram of spacecraft dynamics model

(1)

利用假设模态法将变形量展开,即有:ufi=Φfiq,其中:Φfi为某一质量微元处前l阶振型所对应的变形量,为3×l阶矩阵,仅与微元位置相关;q为柔性附件的模态坐标,为l×1阶矩阵,仅与时间相关.利用模态坐标与变形量的关系可将质量微元的位置与速度写为

(2)

(3)

柔性附件的动能为

(4)

其中,

上述推导过程中忽略了部分量级较小且不影响演化过程卫星守恒量的耦合项,并且认为柔性部件固连于中心体,连接处无间隙且无相对运动.式(4)中右侧3项分别为柔性附件随中心体转动动能、振动动能和转动-振动耦合动能.

另外,柔性附件在振动过程,其弹性形变会产生弹性势能,可表示为[17]

V=UTKUU=qTKqq

(5)

其中:U为所有柔性附件质量微元变形量组成的矢量;KU为所有质量微元对应的刚度矩阵,维数与质量微元个数相关;Kq为模态坐标q对应的刚度矩阵,维数与模态坐标维数相关.

航天器的总动能为中心体动能与柔性附件动能之和,总能量为航天器的总动能和柔性附件弹性势能之和,航天器的拉格朗日量为总动能和柔性附件弹性势能之差,根据式(1)、式(4)与式(5),航天器总能量Es和拉格朗日量L具体写为

(6)

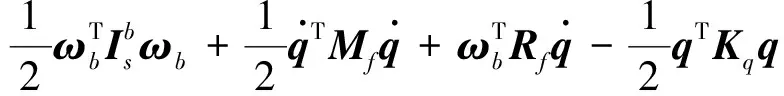
(7)

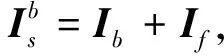
为便于后续分析,对各附件的运动描述方式进行调整:

(8)

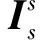
2)对模态坐标进行归一化处理[17],选取新的模态坐标η并令q=Fη,其中F为2类模态坐标之间的转换矩阵,且满足FTMfF=E3.

那么式(7)所示的拉格朗日量可以写作

(9)

其中:ωs=Asbωb,是系下航天器的角速度;Rsf=FRf;Λ为柔性附件频率对角阵.

本文认为帆板振动过程中的阻尼作用强度与弹性形变成正比,即采用线性阻尼模型,并且认为能量耗散仅由柔性部件振动引起,忽略星上液体晃动引起的能量耗散.根据文献[18],柔性附件能量耗散的瑞利耗散函数可以写作

(10)

其中,ξ为柔性附件阻尼比.

根据拉格朗日方程,不考虑外部输入时航天器动力学方程可以表示为

(11)

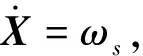
(12)

(13)

将式(12)与式(13)合写成矩阵形式,有

(14)

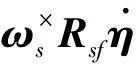
2 航天器不同自旋状态稳定性分析

根据控制论,当系统处于能量最低点时,系统是稳定的,本节将分析航天器能量最低时的运动状态.

根据角动量定理,航天器不受外力矩时,惯性系下角动量的大小与方向均保持恒定.由式(3)与式(9),航天器在系下的角动量可以表示为

(15)

引入拉格朗日函数

(16)

其中,λ为拉格朗日乘子.

显然,当L′取得最小值时,航天器处于能量最低状态.当式(17)～(19)均为0时,航天器总能量Es取得极值

(17)

(18)

(19)

根据计算,航天器总能量处极值时有3组可能的运动状态:

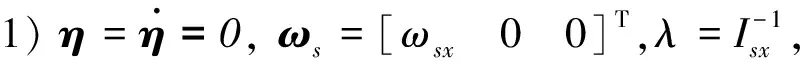
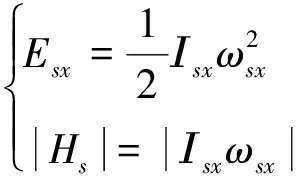
(20)

上述分析中Isx、Isy与Isz分别为航天器绕Xs轴、Ys轴与Zs轴的转动惯量.显然航天器自旋轴惯量越大,总能量越小,故航天器只有绕其最大惯量轴的自旋运动是稳定的.并且由于柔性附件振动过程会逐渐耗散能量,经过足够长的时间后,航天器运动状态均会收敛至绕最大惯量主轴自旋.

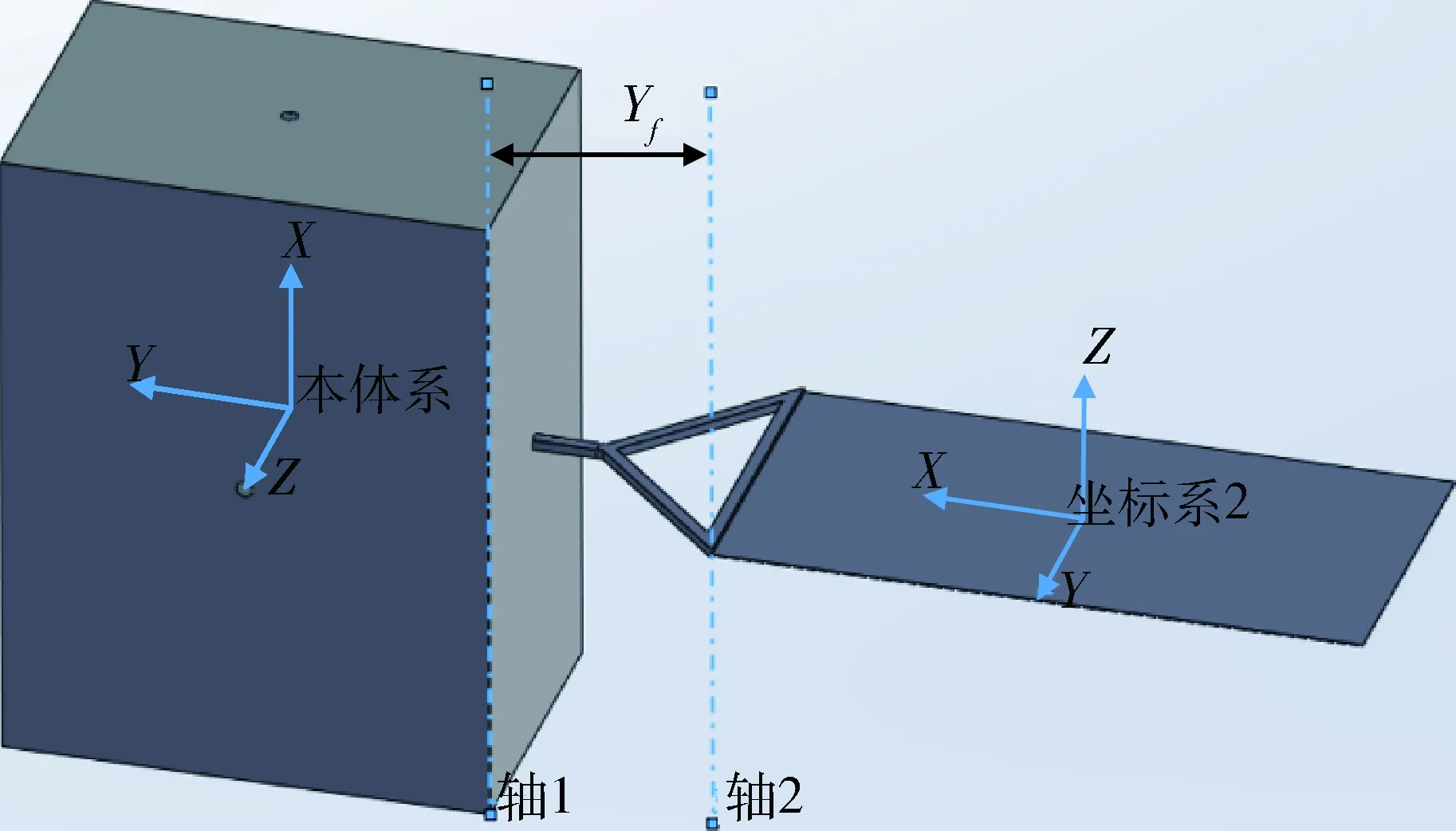
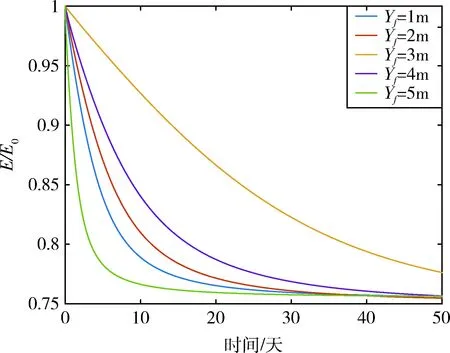
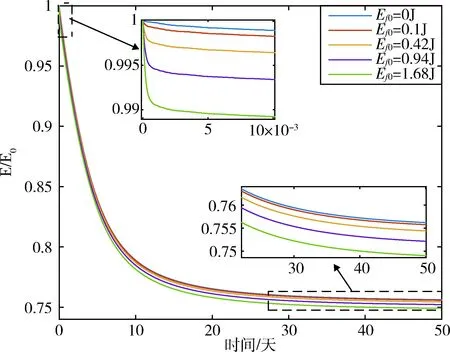
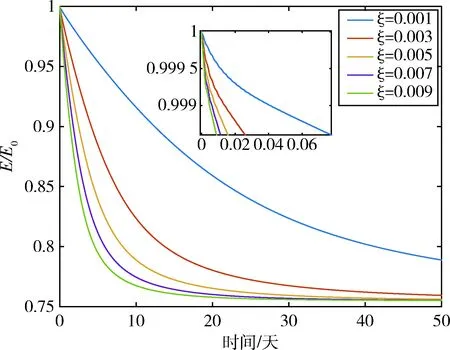
另外根据文献[17],对于满足Isx=Isy=It

(21)

3 能量耗散影响因素分析

上一节的定性分析表明,航天器在柔性部件能量耗散作用下,经过长期运动演化将稳定于绕最大惯量轴自旋的运动状态,本节将基于数值仿真分析影响能量耗散速率的因素,并从能量耗散角度分析柔性卫星的运动演化趋势.

柔性附件的安装方式如图3所示,部分仿真参数如下:

图3 柔性附件的安装示意图Fig.3 Installation diagram of flexible attachments

柔性附件前三阶固有频率分别为0.5 Hz、1.8 Hz和6.2 Hz,柔性附件的前三阶振型如图4所示.

图4 柔性附件前三阶振型Fig.4 First three vibration modes of flexible attachments

(1) 航天器初始角速度对能量耗散速率的影响

图5中给出了不同初始角速度条件下,航天器能量耗散的趋势,其中横坐标为时间,纵坐标为当前时刻能量与初始时刻能量的比值,可以看出,航天器初始角速度越大,能量耗散速度越快.

图5 卫星初始角速度对能量耗散速率的影响Fig.5 Influence of initial angular velocity on energy dissipation rate

图5中的5组算例中,航天器在初始时刻均处于自旋与章动的复合运动状态,且根据各算例角速度初值可知其章动角均相同(7°左右).当航天器三轴角速度均为2(°)/s左右时,经过50天航天器仍具有初始时刻99.89%的能量,即航天器的运动状态几乎没有改变;而当三轴初始角速度为10(°)/s左右,50天后航天器只具有初始时刻77.4%的能量,根据相应曲线可知此时航天器章动已经大幅收敛,接近绕最大惯量主轴自旋的稳定运动状态.根据航天器的转动动力学方程式(12),考虑到长期无控运动过程中柔性附件振动较弱,忽略模态坐标相关项后可以得到

(22)

(2)柔性附件的安装位置对能量耗散速率的影响

图6给出了柔性附件安装位置不同时,航天器能量耗散的趋势.其中Yf是柔性附件距中心体的距离,如图3所示.根据式(4)中If的表达式与式(8)中航天器惯量主轴坐标系的分析,柔性附件不同的安装位置会影响航天器的质量分布,而不同的质量分布特性会导致式(22)右侧各角速度乘积项的系数不同,从而改变航天器能量耗散速度.航天器质量分布越分散,各主轴惯量之差越大,航天器能量耗散速率就越快.

图6 柔性附件的安装位置对能量耗散速率的影响Fig.6 Influence of installation status of flexible attachments on energy dissipation rate

(3)柔性附件初始振动状态对能量耗散速率的影响

图7给出了柔性附件初始振动状态不同时,航天器能量耗散的趋势.Ef0为柔性附件的初始振动能量,包括弹性势能与振动动能.从图7左上子图中可以看出,当柔性部件在初始时刻存在弹性形变时,航天器将在100 s内迅速耗散掉初始弹性势能,并在被自旋运动激发的受迫振动过程中继续耗散航天器能量,此时的能量耗散速度与初始振动状态无关,而图7右下子图说明不同初始振动状态的航天器在末状态时剩余能量基本一致,故航天器初始振动状态对能量耗散速率基本无影响.

图7 初始振动状态对能量耗散速率的影响Fig.7 Influence of initial vibration state on energy dissipation rate

(4)柔性附件材料特性对能量耗散速率的影响

图8给出了柔性附件阻尼比不同时,航天器能量耗散的趋势,当阻尼比为0.009时,航天器可在22天左右时收敛至绕最大惯量主轴的运动;而阻尼比为0.005时,航天器在45天左右时收敛至绕最大惯量主轴的运动,阻尼比为0.001时,航天器在50天时仍未收敛至绕最大惯量主轴的运动.也就是说,柔性附件阻尼比越大,能量耗散速度越快,这一结论可以由式(10)的能量耗散函数直接得到.

图8 柔性附件材料特性对能量耗散速率的影响Fig.8 Influence of material characteristics of flexible attachments on energy dissipation rate

4 结 论

本文针对失效卫星的救援与维护任务设计需求,建立了适用于携带柔性附件航天器长期在轨演化分析的姿态-振动耦合动力学模型,从理论上分析了不同自旋状态的稳定性,并研究了航天器能量耗散速度的3种主要影响因素.所得出的主要结论如下:

1)针对所研究的不同问题背景,应有选择地简化航天器动力学模型,在失效卫星长期运动演化分析中,为保障分析结果的精度,应保持航天器角动量守恒,故研究中应避免简化掉过多耦合项;

2)航天器绕不同空间轴自旋时,若航天器角动量一定,则自旋轴惯量越大,航天器能量越小,并且由于柔性附件振动会导致持续的能量耗散,航天器经过足够长时间的运动演化后均会收敛至绕最大惯量轴的自旋运动,但这一过程耗时很长;

3)根据理论分析与数值仿真,柔性航天器能量耗散速率主要与卫星初始角速度、柔性附件的安装位置、柔性附件材料特性等因素相关,而柔性附件的初始振动状态对能量耗散速率影响很小.