基于ANSYS的铝合金球淬火热分析

李勇进 马迎松 屈浩宇 樊力中

摘 要：利用ANSYS APDL有限元瞬态分析法，建立铝合金球Al-Si-Cu-Mg的有限元模型及其淬火温度场，求解后得到淬火过程中的应力场与温度场等结果。在油和水2种不同的介质下进行淬火并完成淬火过程的有限元模拟，可以观察到淬火过程中合金球各个位置的温度变化和冷却速度变化，以及在油淬和水淬2种情况下的合金球淬火过程的差异。结果表明：合金球在考虑自身重力的影响下，其底部表面位置为其所受最大拉压应力处；合金球所有位置在水冷淬火条件下的冷却速度要比油冷淬火条件下的冷却速度快；水冷淬火条件下底部的等效应力以及第一、二、三主应力都比油冷淬火条件下的受力下降的快。

关键词：ANSYS；有限元；Al-Si-Cu-Mg；水冷淬火；油冷淬火

中图分类号：TG156.3 DOI：10.16375/j.cnki.cn45-1395/t.2023.01.016

0 引言

铝合金构件经过固溶处理可得到高强度高硬度的合金，在此过程中，为防止脱溶析出会对铝合金构件进行快速淬火，得到高出饱和度的固溶体[1]。淬火速率、淬火介质不同，其淬火时会发生不一样的改变，因而在淬火结束后所得到的材料性能不同，淬火速率高，获得的材料性能相对好[2]。在淬火中对构件进行快速冷却，会让构件内外部产生温度传递延迟现象，导致构件存在较大的温度梯度，材料冷却收缩不均匀，影响、破坏材料的性能[3]。其淬火过程中产生的残余应力等升温变化会使得构件的力学性能、抗拉强度以及耐蚀性能等受到极大的影响[4]。

随着计算机技术的发展，科研人员进行了大量的关于淬火过程的数值模拟分析。有限元数值仿真分析是铝合金材料淬火研究中应用最多的分析方法[5]，运用有限元仿真技术可以细致地观察到淬火过程中温度场的变化规律以及应力场变化规律等[6]。袁青尧[7]使用ABAQUS对航天铝合金大型构件淬火进行了仿真模拟，对其温度场、应力场进行了有限元仿真研究。

常用的有限元软件有ABAQUS、ANSYS等，对比ABAQUS软件，ANSYS建模更为简便，应用领域更广，其模拟的环境更加接近真实情况，更倾向于从有限元角度考虑问题。本文采用有限元软件ANSYS APDL[8]对铝合金淬火进行建模仿真。考虑到构件自身重力的影响，在2种不同介质下进行淬火，探索铝合金Al-Si-Cu-Mg淬火过程中合金球内的温度变化、变形情况、应力变化以及不同介质下进行淬火的效果，为后期铝合金的工艺优化等提供参考。

1 理论基础

研究表明，传热体与环境换热关系的边界条件和热传导通用方程可以作为构件淬火热传导过程的分析工具，分析传热体和环境换热关系，模拟铝合金淬火。对能量守恒定律和傅里叶传热定律进行研究推导，得到瞬态温度场[T（x，y，z，t）]方程来描述铝合金的淬火传热[9]：

初始条件：[T |t=t0=T0（x，y，z，t） ].

边界条件：

①第一类边界条件：

[T（x，y，z，t）=T0（x，y，z，t），  x， y， z∈Γ1].

②第二类边界条件：

.

③第三类边界条件：

.

式中：T为瞬时温度；T0为初始温度；Tw、Tc分别为工作表面温度、介质温度；λ表示材料的导热系数；Cp表示比热容；ρ为密度；t為时间；Q为材料内部热源强度（即相变潜热和塑性功生成热）；n为方向余弦；[q0]为热流密度；Hf为总的换热系数。在铝合金的淬火过程中，合金表面温度快速变化，且变化波动较大，所以第一类边界条件被舍弃。第二类、第三类边界条件差别不大，在本质上是一样的，又因为合金外部与环境介质的换热系数由实验测试得到，其数值随温度变化而变化，所以，在实际应用过程中一般选择第三类边界条件。

2 淬火过程的有限元模型

2.1 有限元模型建立

采用ANSYS APDL软件作为有限元分析模拟平台，使用ANSYS APDL有限元瞬态分析法[10]。选用耦合三维20节点SOLID226单元对合金球进行单元属性赋予，有限元模型为一个实体圆，取其半径为0.1 m的实体结构建模。其网格尺寸选择0.01，网格划分后的有限元模型如图1所示。

2.2 材料参数

将合金球加热到一定温度后停止加热，加入淬火介质进行合金球的淬火，因此，设定淬火前合金球的初始温度为500 ℃，淬火介质为 20 ℃的水和油。Al-Si-Cu-Mg合金球的化学成分及其质量分数如表1所示。合金球的热物性参数通过JMatPro7.0软件计算得出[11]。

2.3 换热系数

反传热法和比拟法是换热系数常用的计算方法。反传热法是利用Deform-3D的反传热模块和实验测得的冷却曲线，建立对应的换热环境，通过模拟得到符合其冷却特性结果的换热系数[12]。比拟法是因为温度传递存在共通的特性，由其换热系数与冷却特性相对应以建立其数学模型，通过这个数学模型可以得到2种介质的量关系，即由其中一种介质的换热可计算出另一种介质的换热系数[13-14]。

数值法是由热力学第一定律以及最小二乘拟合法计算目标函数冷却速度v的数学表达式，以此建立冷速温度变化曲线图，得到一定温度下不同环境介质的换热数值。

比拟法[15]简洁便利，可以快速地由不同介质的特性建立数学关系模型，通过这个关系可计算出介质的换热系数，即将一种介质的换热代入关系桥梁计算出目标介质的换热系数。本文中，铝合金在水中淬火的换热系数已知，要得到介质油的换热系数，需建立油和水的数学关系模型，通过已知换热系数极值与冷速极值的关系，推导出介质油的换热能力几乎只有水换热特性的1/3。使用惯用曲线描述水的换热特性曲线，以此得到铝合金在水和油中淬火的换热系数，如图2所示。

2.4 边界条件设置

如图2所示设置合金球对流换热系数，施加对流边界条件，其换热的淬火介质温度设置为20 ℃。根据实际工程条件进行模拟，对建立的模型进行相对应的设置。模拟实验开始时，首先将铝合金球置于淬火介质中，初始温度设置为500 ℃。由于重力合金球处于容器底部，其底部与容器相接触，需要在其底部施加位移约束，并给模型施加817 N的重力载荷。设置淬火时间为100 s，其载荷步设置为100步，最大载荷步为10，最小载荷步为1。对模型进行如上设置后，对模型进行求解分析。

3 淬火过程仿真分析

3.1 温度场分析

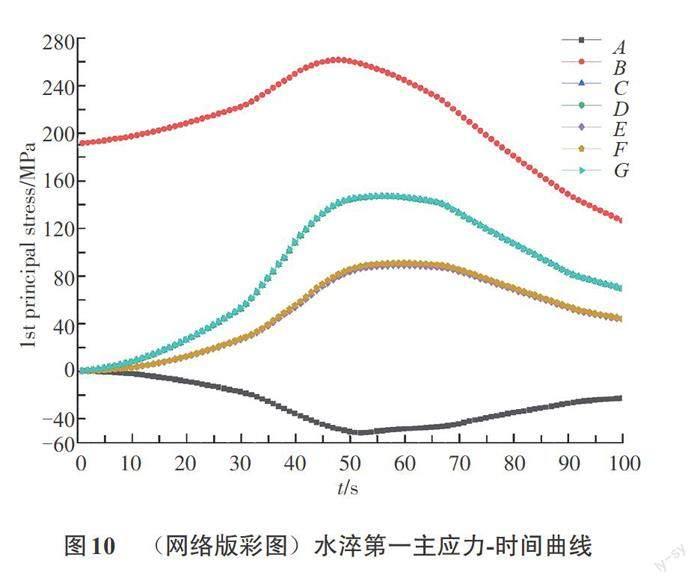
合金球为轴对称结构，选取其对称结构的部分节点进行分析。从合金球的圆心位置进行剖面得到其剖面图如图3所示。关键节点处的变化曲线，其名称用关键节点处字母表示：A——圆心处；B——圆底部；C——圆顶部；D——圆的最侧面；E——圆心距底部的中间位置；F——圆心距最侧面的中间位置；G——圆心距顶部的中间位置。

图4—图8为水淬合金球各位置的温度随时间变化的示意图，由此能定量分析合金球各区域的温度场变化。分析可知，在淬火的过程中，初期合金球冷却速度最快的位置是其表面处，其次是圆心到表面的中间位置，圆心处冷却速率最低，合金球的圆心处在50 s时温度被降低至425 ℃；随着淬火的进行，合金球的圆心处冷却速率开始增加，合金球的表面位置冷却速率开始变小；合金球的速度矢量和与加速度矢量和都存在一个相同的特点，合金球底部位置的速度矢量和与加速度矢量和都为最小值，而顶部位置的速度矢量和与加速度矢量和的值都为最大，整个合金球的速度矢量和与加速度矢量和都是由底部向顶部逐步提高、逐层递进。

3.2 应力场分析

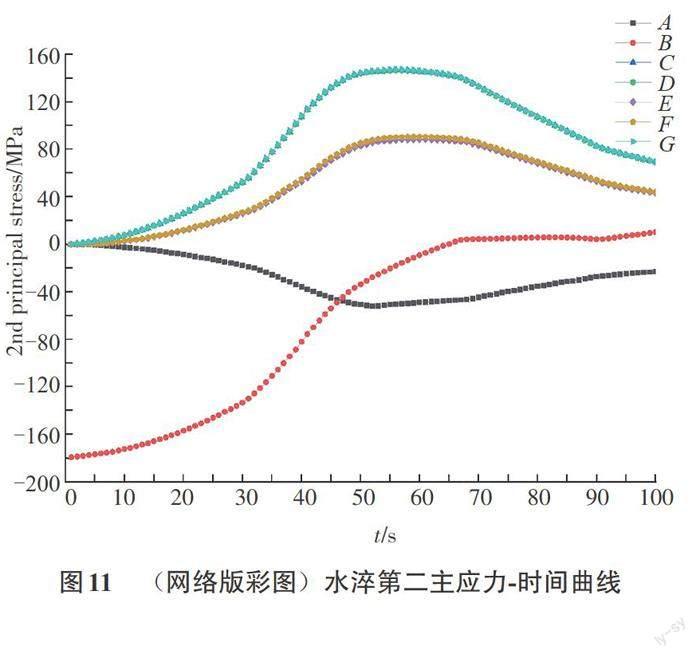
由铝合金放置在平面的Von Mise应力云图（图5）以及水淬等效应力-时间曲线图（图9）可知，合金球的Von Mises应力最大值在底部，为455.96 MPa，其次在圆心与顶部的过度区域，最小受力处为圆心处。由图9—图12可知，合金球底部位置受自身重力作用冷却，其受到的等效应力、主应力也开始逐渐变小，整个淬火过程中合金球受到最大拉应力以及最大压应力都集中在其合金球的底部位置。在淬火过程中，除底部位置外，合金球其他位置的受力情况都是：受到的应力先快速增加，然后达到饱和，再随着温度的降低而降低。

3.3 水淬与油淬的对比

图8—图12为水冷淬火图，图13—图17为油冷淬火图。将水冷淬火与油冷淬火进行对比可知：合金球在水冷淬火的条件下，所有位置的冷却速度都比油冷淬火条件下的速度快；其合金球底部的应力减小速度快于油冷淬火条件下的应力减小速度，在100 s时，水淬后其等效应力降低到155 MPa，而油淬后只是降低到240 MPa，合金球其他位置的等效应力不随淬火介质的变化而变化；水淬条件下，其底部的第一主应力比油淬条件下减小的快，在100 s时，水淬后其第一主应力降低到125 MPa，而油淬后只是降低到162 MPa；水淬条件下其圆心距顶部的中间位置比其圆心距最左侧的中间位置受力小，而油淬条件下情况正好相反，其圆心距顶部的中间位置比其圆心距最左侧的中间位置受力大，且它们受力大小几乎相等，合金球其他位置受力情况基本不随淬火介质的变化而变化；水淬条件下，其底部的第三主应力比油淬条件下减小的快，在100 s时，第三主应力降低到50 MPa，而油淬后只是降低到105 MPa，合金球其他位置的第三主應力不随淬火介质的变化而变化；水淬条件下，合金球除了底部位置外，各位置的第二主应力基本与油淬条件下的第二主应力相同，其受力大小几乎不变而受力方向发生变化。

4 结论

1）合金球淬火初始阶段，合金球表面处冷却速率最快，其次是圆心到表面的中间位置，圆心处冷却速率最低；随着淬火的进行，合金球圆心处的冷却速率增加，表面的冷却速率逐渐减小。合金球底部位置的速度矢量和与加速度矢量和都为最小值，而顶部位置都为最大值，整个合金球的速度矢量和与加速度矢量和都是由底部向顶部逐步提高、逐层递进。

2）合金球的Von Mise应力最大值在底部，其次为圆心与顶部的过渡区域，最小受力处为圆心处。整个淬火过程中其最大拉应力以及最大压应力都集中在了其合金球的底部位置。在淬火过程中，除底部位置外，其他位置受力情况基本都是应力先快速增大，然后达到饱和，再随着温度的降低而减小。

3）合金球在水冷淬火条件下，所有位置的冷却速度都比油冷淬火条件下的速度快，其底部的等效应力和第一、二、三主应力相比油冷淬火条件下要减小的快，其他位置的等效应力不随淬火介质的变化而变化。

4）水淬条件下合金球圆心距顶部的中间位置比其圆心距最左侧中间位置的第一主应力小，而油淬条件下情况正好相反，2种淬火条件下它们受力大小几乎相等，其他位置第一主应力受力除底部外基本不随淬火介质的变化而变化。

5）水淬条件下，合金球各个位置的第二主应力与油淬条件下的第二主应力基本相同，除了底部位置外，其受力大小几乎不变而受力方向发生变化。

参考文献

[1] LIM S T，YUN S J，NAM S W.Improved quench sensitivity in modified aluminum alloy 7175 for thick forming applications[J].Materials Science and Engineering A，2004，371（1-2）：82-90.

[2] 韩金军，李涛.不同淬火介质下2A12铝合金的剥层腐蚀研究[J].新技术新工艺，2021（10）：66-69.

[3] 徐宁，王爽，潘岩，等.淬火冷却速率对6082铝合金组织及性能影响研究[J].有色金属加工，2021，50（6）：10-13.

[4] 罗海云，吴道祥，王彬，等.7050铝合金H型截面构件淬火过程仿真模拟研究[J].铝加工，2019（4）：19-22.

[5] 顾南荣，吴辉琴，刘显晖，等.球型支座测力系统设计及测力试验分析[J].广西科技大学学报，2022，33（2）：33-40，47.

[6] 于春鹏，王立强，汤贞涛，等.铝合金大型锻件淬火过程的有限元模拟[J].金属热处理，2021，46（9）：279-283.

[7] 袁青尧.基于UMAT的航天铝合金大型构件淬火变形预测研究[D].哈尔滨：哈尔滨工业大学，2019.

[8] 郝子龙，石光林.基于ANSYS的平板堆焊凝固过程的应力分析[J].广西科技大学学报，2016，27（1）：54-57.

[9] 曹金荣，杨杨，王楠林.7075铝合金淬火残余应力的计算与测定[J].铝加工，1998（3）：42-44.

[10] 钟流发，刘祚时.基于ANSYS的汽车半轴法兰盘感应淬火热分析[J].热加工工艺，2020，49（14）：114-118.

[11] 宋峰，毛红奎，阎志义，等.铝合金气缸盖淬火过程的残余应力有限元模拟分析研究[J].热加工工艺，2022，51（10）：127-130.

[12] 隋佳丽.大型风电主轴淬火过程有限元仿真[D].济南：山东大学，2019.

[13] 张伟，彭飞，冯翠花，等．水流速对表冷器传热系数影响的分析[J]．制冷空调与电力机械，2009，30（6）：50-52，70.

[14] 周澍，陈乃录，张伟民，等．水在不同温度和流速下冷却能力的测量[J]．金属热处理，2008（6）：69-72.

[15] 王春林．科技编辑大辞典[M].上海：第二军医大学出版社，2001.

Thermal analysis of aluminum alloy ball quenching based on ANSYS

LI Yongjin， MA Yingsong*， QU Haoyu， FAN Lizhong

（School of Mechanical and Automotive Engineering， Guangxi University of Science and Technology， Liuzhou 545616， China）

Abstract： The finite element model and the quenching temperature field of Al-Si-Cu-Mg aluminum alloy ball were established by using ANSYS APDL finite element transient analysis method， and the results of stress field and temperature field in the quenching process were obtained after the solution. The finite element simulation of the quenching process was completed by quenching in two different media， oil and water， then the temperature change and cooling rate change at each position of the alloy ball during the quenching process and the difference in the quenching process in the two cases could be observed. The result shows when considering the influence of its own gravity， the position of the bottom surface of the alloy ball was the place where the alloy ball was subjected to the maximum tensile and compressive stress. The cooling rate of all positions of the alloy ball under the condition of water-cooling quenching was faster than that of oil-cooling quenching. Under the condition of water-cooled quenching， the equivalent stress and the first， second， and third principal stresses at the bottom all decreased faster than those under the condition of oil-cooled quenching. These conclusions may provide help for the optimization of the subsequent quenching process of aluminum alloys.

Key words： ANSYS; finite element; Al-Si-Cu-Mg; water-cooled quenching; oil-cooled quenching

（責任编辑：黎 娅）