2016-2021年高中数学联赛初赛数列试题对比研究

肖刚　魏苗　刘艺　马杰

摘 要：文章在已有研究的基础上，对2016-2021年全国大部分地区高中数学联赛初赛试卷中的数列试题进行了分析探究.文章将数列试题归纳整理成了求通项公式、数列求值、数列求和、与函数方程结合、与不等式结合、概率计算、存在性问题、数学归纳法、数列创新定义及其他探究类型十大类.

关键词：高中数学联赛初赛；数列；试题研究

中图分类号：G632 文献标识码：A 文章编号：1008-0333（2023）18-0005-03

收稿日期：2023-03-25

作者简介：肖刚（1990-），男，四川人，硕士，助教，从事数学教学研究；

刘艺（1998-），女，四川人，硕士，助教，从事数学教学研究；

魏苗（2000-），女，四川人，在读本科，从事数学教学研究；

马杰（1978-），男，四川人，本科，高级教师，从事数学教学研究.

基金項目：宜宾学院校级一流本科专业“数学与应用数学”项目（项目编号：409-XYLZY202101）

1 研究缘起

数列是高中数学联赛初赛的必考内容之一，由于数列知识的命题灵活度高，成为数学联赛的一大难点，参赛选手若能够攻克这一难点，相信对提高其竞赛成绩定有所帮助.另外，国内关于专门研究高中数学联赛初赛数列试题的文章较少，因此笔者希望通过文章的论述，能够为此问题的研究提供一些参考.最后，数列试题往往知识容量大，题目的综合性较高，对学生的思维能力、创新能力以及运算能力有较高要求，若是学生对数列试题有所突破的话，相信能很大程度地提高其数学素养.

2 研究设计

2.1 研究对象

文章以2016-2021近六年的高中数学联赛初赛数列试题作为研究对象，主要从高中数学联赛概述及要求、高中数列知识纲要、高中数学竞赛数列问题的十大题型这几个方面进行分析.

2.2 研究思路及方法

文章主要采用了文献研究法和实践分析法.

采用文献研究法，从而全方位地、准确地了解研究者们对数列问题的历史研究进展.

采用实践分析法，文章收集了2016-2021近六年的高中数学联赛初赛中的数列试题，通过对其考核规则与能力要求、题型、题目的数量、题目的分值、各省份出现的数列题目异同等方面进行分析比较.

3 研究结论

文章选取2016-2021近六年里，全国大部分地区自行组织的高中数学联赛初赛的真题进行统计分析，数据来源于中国数学会普及工作委员会及各省市数学会联合编写的《高中数学联赛备考手册》.

3.1 横向数据对比

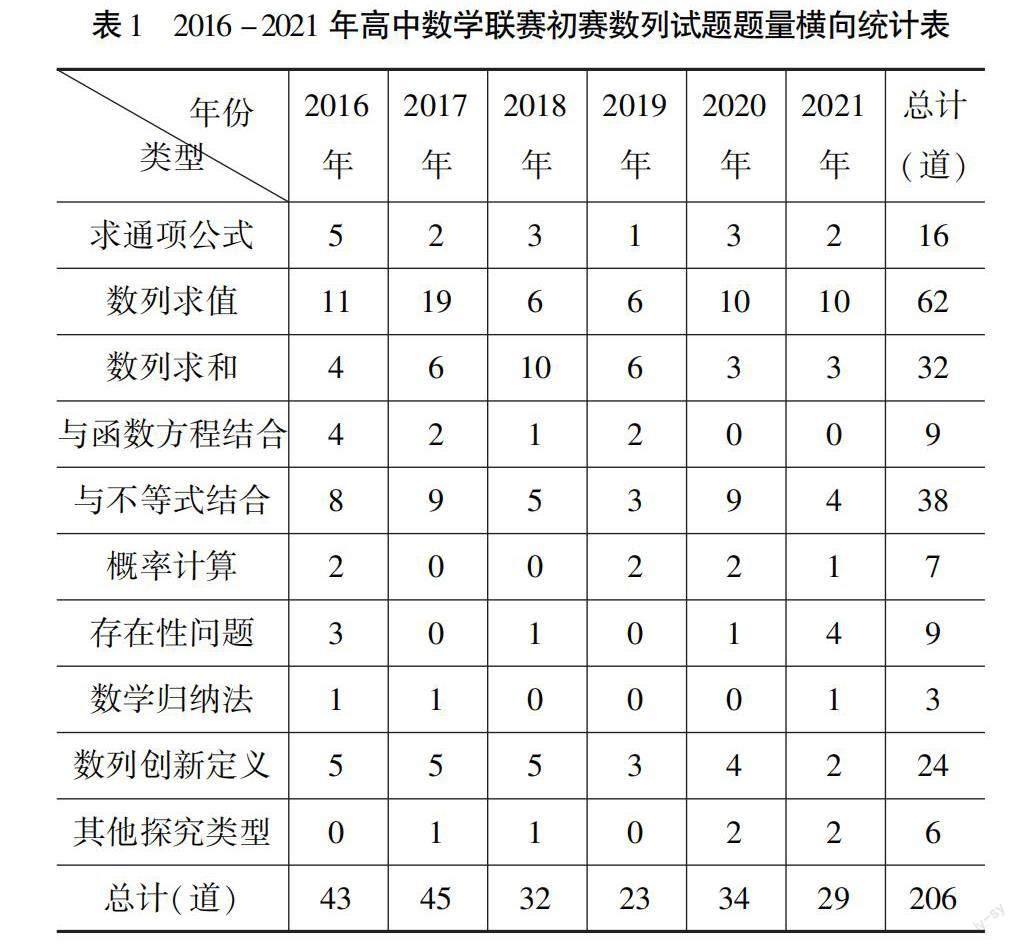
通过统计2016-2021近六年的高中数学联赛初赛数列试题发现，可以将试题的提问方式归类为以下几种类型：求通项公式、数列求值、数列求和、与函数方程结合、与不等式结合、概率计算、存在性问题、数学归纳法、数列创新定义以及其他探究类型.下面，对2016-2021年高中数学联赛初赛数列试题题量进行统计分析，具体见表1.

对上述表格的内容进行分析，可以得到以下一些信息：

从每年数列试题题量的占比上看，2016年的占比约为20.87%，其中，数列求值类考查了11道，考查次数最多，约占2016年的25.58%；2017年的占比约为21.84%，其中，数列求值类考查了19道，考查次数最多，约占2017年的42.22%；2018年的占比约为15.53%，其中，数列求和类类考查了10道，考查次数最多，约占2018年的31.25%；2019年的占比约为11.17%，其中，数列求值类和数列求和类考查了6道，考查次数最多，都约占2019年的26.09%；2020年的占比约为16.50%，其中，数列求值类考查了10道，考查次数最多，约占2020年的29.41%；2021年的占比约为14.08%，其中，数列求值类考查了10道，考查次数最多，约占2021年的34.48%.

从题型的集中与分散程度上来看，2016-2021年每年考查的题型大致相同.

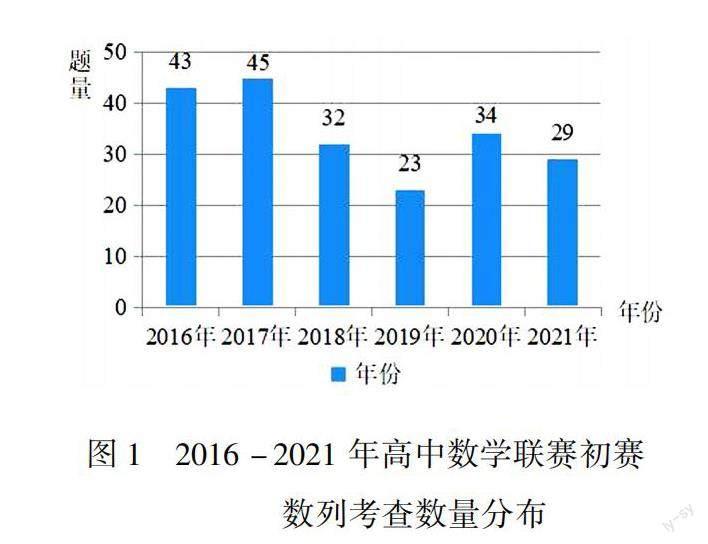
从表1中的信息可以看出，近六年来的数列试题考查数量较为失衡，具体见图1.

从图1可以看出，2016-2021近六年高中数学联赛初赛中数列题的考查数量波动较大.2016年、2017年都多于了40题，2018年和2019年都少于了40题.到了2020年突然上升，达到了34题.2021年又突然减少，与2020年相比，少了5道题.

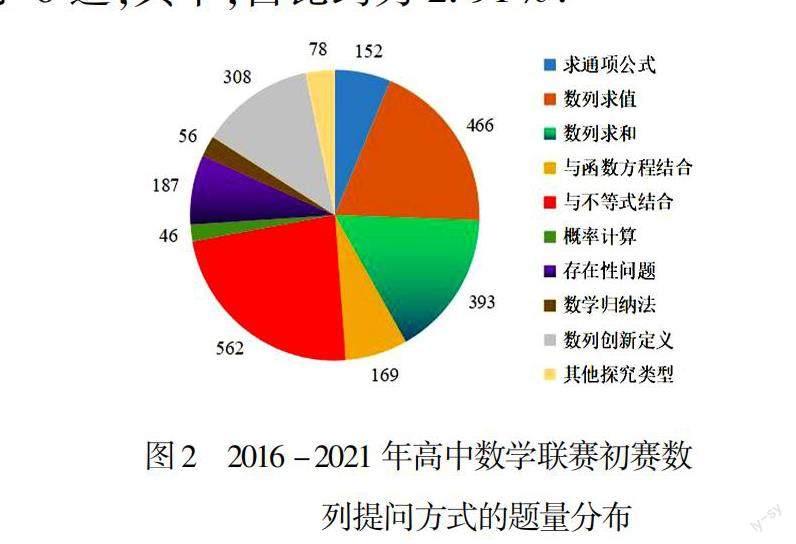
从每年数列题目的提问方式上来看，数列求值问题是近六年数列题中最常考的题目类型，其次是与不等式结合的问题.具体见图2.

从图2可以得出，2016-2021近六年高中数学联赛初赛的数列题中，“求通项公式”类考了16道，其中，占比约为7.77%；“数列求值”类考了62道，其中，占比约为30.10%；“数列求和”类考了32道，其中，占比约为15.53%；“与函数方程结合”类考了9道，其中，占比约为4.37%；“与不等式结合”类考了38道，其中，占比约为18.45%；“概率计算”类考了7道，其中，占比约为3.40%；“存在性问题”类考了9道，其中，占比约为4.37%；“数学归纳法”类考了3道，其中，占比约为1.46%；“数列创新定义”类考了24道，其中，占比约为11.65%；其他探究类型考了6道，其中，占比约为2.91%.

下面，对2016-2021年高中数学联赛初赛数列试题的分值进行统计分析，具体见表2.

对表2的内容进行分析，可以得到以下一些信息：

从每年考查数列试题的分值上看，2016年共计502分，2017年共计516分，2018年共计424分，2019年共计263分，2020年共计388分，2021年共计324分，总共2417分.

从每年考查数列试题分值的占比上看，2016年的占比约为20.77%，其中，与不等式结合类查了105分，分值最高，约占2016年的20.92%；2017年的占比约为21.35%，其中，数列求值类考查了149分，分值最高，约占2017年的28.88%；2018年的占比约为17.54%，其中，数列求和类考查了129分，分值最高，约占2018年的30.42%；2019年的占比约为10.88%，其中，数列求和类考查了68分，分值最高，約占2019年的25.86%；2020年的占比约为16.05%，其中，与不等式结合类考查了154分，分值最高，约占2020年的39.69%；2021年的占比约为13.41%，其中，数列求值类考查了68分，分值最高，约占2021年的20.99%.

从表2中的信息可以看出，近六年来的数列试题所占分值较为失衡，具体见图3.

从图3可以得出，2016-2021近六年高中数学联赛初赛中数列试题所占分值波动较大.2016年、2017年所占分值相对高一些，大于500分，2018年其次，大于400分，2020年、2021年大于300分，2019年所占分值相对低一些，小于300分.

从每年数列题目的提问方式上来看，与不等式结合问题是近六年数列题中所占分值最高的，其次是数列求值的问题，而概率计算的问题所占分值较低.具体见图4 ：

从图4可以得出，2016-2021近六年高中数学联赛初赛的数列题中，“求通项公式”类所占分值为152，其中，占比约为6.29%；“数列求值”类所占分值为466，其中，占比约为19.28%；“数列求和”类所占分值为393，其中，占比约为16.26%；“与函数方程结合”类所占分值为169，其中，占比约为6.99%；“与不等式结合”类所占分值为562，其中，占比约为23.25%；“概率计算”类所占分值为46，其中，占比约为1.90%；“存在性问题”类所占分值为187，其中，占比约为7.74%；“数学归纳法”类所占分值为56，其中，占比约为2.32%；“数列创新定义”类所占分值为308，其中，占比约为12.74%；其他探究类型所占分值为78，其中，占比约为3.23%.

参考文献：

[1]叶诚理.新课程下开展高中数学竞赛的实践和认识[D].福州：福建师范大学，2009：1-2.

[2] 杨茜.全国高中数学联赛之数列问题研究[D].西安：西北大学，2016：1-2.

[3] 姜莹莹.融合高等数学与初等数学竞赛思想方法提升中学师生素养的研究[D].南宁：广西民族大学，2019：8-9.

[4] 逢萌.高中数学竞赛中的数列问题研究[D].开封：河南大学，2020：2-3.

[5] 孟祖国.高中数列的有效教学研究[D].武汉：华中师范大学，2011，19-20.

[责任编辑：李 璟]