基于权重控制的齿面重构技术及有限元分析
张凯杰,岳坤明,薛 浩
上海理工大学 机械工程学院,上海 200093
1 引 言
螺旋锥齿轮由于重合系数大、承载能力强、传动效率高、传动平稳[1]等优势被广泛应用于各种交错轴传动的机械设备中。近几年来,数字化虚拟技术[2]被广泛应用于螺旋锥齿轮的设计中,用来指导螺旋锥齿轮的实际加工。由于螺旋锥齿轮的齿面形状复杂,因此,很多学者针对齿面重构进行了研究,其中NURBS拟合函数得到广泛应用。Rui等[3]利用最小二乘法对NURBS拟合后的齿面进行二次优化逼近,相比于CAD/CAM中立方体非均匀有理B样条曲线和曲面的拟合技术,齿面的精度明显提高;林家春等[4]对齿面测量点进行NURBS曲面拟合,并建立真实齿面的三维参数化模型,将建立的参数化模型与理论模型比较得出齿廓偏差,解决了特大型齿轮特征线的测量问题;丁撼等[5]结合三次NURBS曲线曲面造型技术的在CAD/CAM中的优势完成球面渐开线齿面的精确拟合,利用蒙皮法构造的NURBS齿面基础上提出相关优化方案,为齿面接触分析提供了齿面数据与基础模型;邓辰等[6]通过循环高斯核的Kriging模型得到齿面控制顶点,进而对双重螺旋法加工的齿面进行重构,再通过数值测量验证了重构齿面的整体精度高,最后通过蒙面法实现了齿面的重构;马力全等[7]详细介绍了双二次NURBS曲线及曲面权重系数的计算方法,去掉了传统方法中对相关矩阵的求逆,并增加了一项顶点系数,该方法能够快速计算出每一个控制顶点的权重系数。大部分齿面重构的研究都只是确保了拟合曲面的最大误差以及平均误差,却忽视了误差的整体分布情况以及是否存在局部过拟合等问题;王笑一等[8]基于齿面误差的3D表达提出了特征数据集的定义方法以及基于统计的齿面误差评价指标计算方法。因此,利用统计学方法诠释齿面误差将更好地反映整体齿面拟合情况。
进行刀倾法虚拟切齿时,小轮齿面呈现碎片式现象,不利于后续的网格划分与有限元分析,因此需要对加工后的齿面进行重构处理。由于接触斑点分布是作为螺旋锥齿轮接触性能以及判断其承载能力的一个重要指标,而接触斑点分布直接取决于重构齿面的情况,因此在进行有限元分析时,齿面误差的随机性可能会导致接触斑点歧义,从而使设计者为达良好接触区域而错误地调整机床参数,从而降低齿轮传动性能。本文采用Newton-Raphson方法确定齿面的中央控制顶点,通过虚拟切齿技术确定齿面的边界,从而实现齿面分区,再基于双二次NURBS曲面权重系数计算方法计算各控制顶点的权重分布,从而实现对各控制顶点间自适应分配插值节点数,使重构齿面的误差在各齿面划分区域上均匀分布,避免了重构齿面的局部失真而降低齿轮接触仿真分析的准确性。
2 基于权重控制的曲面重构
曲面重构方法分为以下4个步骤,如图1所示:

图1 曲面重构流程图Fig.1 Flowchart of surface reconstruction
以一对准双曲面齿轮副为研究对象,基于格里森制的HFT计算卡解析[9]刀倾法加工的小轮以及成形法加工的大轮,通过Visual Basic程序对轮坯进行参数计算,并利用CATIA二次开发进行参数化建模。根据螺旋锥齿轮的切齿加工原理,推导出轮坯与刀具之间的初始相对位置以及运动关系,通过CATIA中的VBA宏程序控制刀具与轮坯的运动。因此先根据小轮加工参数使刀具相对于轮坯进行空间定位,再通过CATIA中的宏命令进行连续切削50次,从而得出小轮齿面上完整的刀痕线,但是这种做法会大大降低齿面精度,故需对小轮齿面进行重构。一般而言,型值点越多,曲面拟合越精确,但是其计算成本也会线性增加,故在保证拟合精度的前提下,应尽量提取较少型值点。
为了使重构后的齿面更好贴合理论齿面,通过引入理论点作为齿面上的面控制顶点,从而进行曲面拟合。由于螺旋锥齿轮的齿面相当复杂,其齿面方程不能通过显示函数进行表达,故本节通过齿面共轭原理[10-11],由Newton-Raphson方法计算表面点的坐标值,这个方法包括坐标变换方程、运动方程以及齿坯边界方程,如式(1)所示:
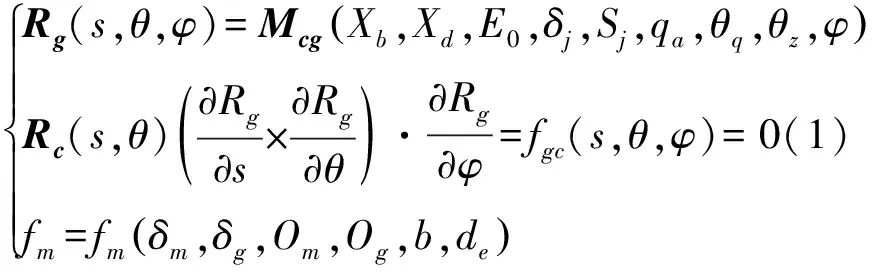
式(1)中,Rg(s,θ,φ)表示齿轮在运动过程中的位置向量;Rc(s,θ)表示刀具在运动过程中的位置向量;Mcg(Xb,Xd,E0,δj,Sj,qa,θq,θz,φ)表示坐标变换矩阵;fgc表示齿轮啮合方程;fm(δm,δg,Om,Og,b,de)表示由设计参数定义的齿轮边界方程。
其中,s为刀刃顶距(mm),θ为刀转角(°),φ为床位(mm),Xb为机床基点到背部的距离(mm),Xd为机床基点到底座的距离(mm),E0为偏移量(mm),δj为机床根角(°),Sj为径向轮位(mm),qa为安装角(°),θq为刀倾角(°),δm为面锥角(°),δg为根锥角(°),Om为面锥顶点到交叉点距离(mm),Og为根锥顶点到交叉点距离(mm),b为齿宽(mm),de为外端直径(mm)。
由上述方程组求解得到曲面上3×7的点阵坐标,计算共轭齿面型值点示意图如图2所示。
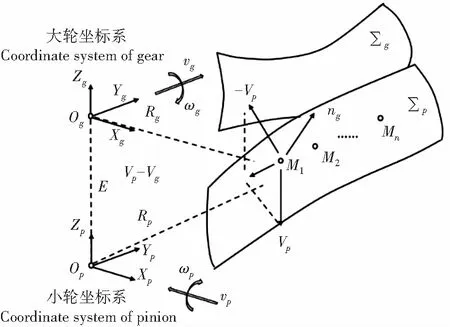
图2 齿面型值点的计算Fig. 2 Calculation of points on tooth surface
2.1 权重计算及曲率调整
2.1.1计算权重系数
双二次NURBS曲面的数学表达式[7]:
(2)
式(2)中,t为规范后的参数变量,t∈[0,1];ωi,j为控制顶点的权重系数;Ni,2(t)为2次B样条基函数。
双二次NURBS曲面拟合的研究中,建立一组合适的权重系数能有效提高曲面拟合精度。由于权重系数能调节曲面形状与控制顶点之间的关系,故调节各点的权重系数会影响该点自身及其相邻点对应的曲面形状。当权重系数增大,曲面就会逼近控制顶点,反之则会远离控制顶点。一个控制顶点的权重系数由其自身和周围的邻点共同确定,对于双二次NURBS曲面而言,计算一个控制顶点的权重系数需要9个顶点。
根据图3的齿面分区示意图,将各区域的顶点作为权重计算的控制顶点。

图3 齿面分区示意图Fig. 3 The sketch of tooth surface partition
由控制顶点本身及其周围的9个点计算出各顶点的权重系数,表达式如式(3)所示:
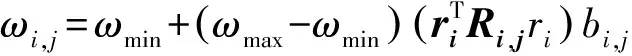
(3)
式(3)中,ri为相关矢量,Ri,j为相关矩阵,bi,j为顶点系数。根据文献[12]可知,ωmin为0.1,ωmax为1.0,ri,Ri,j,bi,j的计算公式如式(4)、式(6)、式(7)所示:
(4)
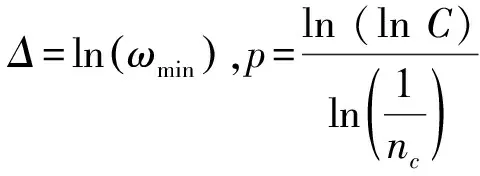
(5)
式(5)中,C为相关系数,一般取2[13];nc为控制顶点数目,故这里nc等于45。

(6)
bi,j=zi,j-zmin
(7)
式(7)中,zi,j为控制顶点在z方向上的坐标值,zmin为45个控制顶点中最小的z值。
上述式(2)—式(7)中的i,j分别表示控制顶点在齿长和齿高方向的下标,i=0,1,…,8;j=0,1,…,4。
曲面控制顶点权重系数传递示意图如图4所示:

图4 权重系数传递示意图Fig. 4 The schematic diagram of weight coefficient

(8)
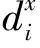
由式(8),计算得小轮凹面的各控制顶点权重系数,其权重分布如图5所示。
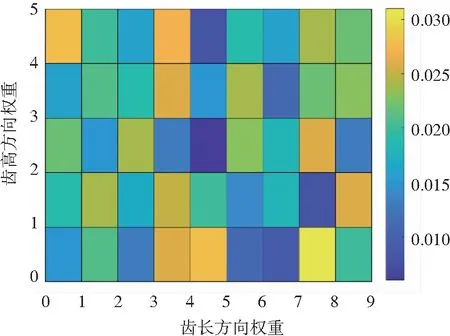
图5 小轮凹面控制顶点的权重分布Fig. 5 Weight distribution of points on pinion concave
2.1.2曲率调整
通过在两两控制顶点间插值,可改变各区域曲面曲率,从而间接影响整体曲面精度。若插值点数量偏少可能导致曲面精度达不到预期要求,而插值数量偏多又会产生“过拟合”现象,反而导致整体或局部曲面精度下降,因此,需要得出各分区控制点间的最优插值点数量。本节将两两控制顶点间的权重系数差值之比转化为各控制点间的插值节点数之比,通过同比例增加各区域插值节点数,直至开始出现局部“过拟合”现象为止,重构齿面的误差均值随插值节点数的增加而呈现“先降低后上升”的趋势,如图6所示,其原因就在于插值点数过多而导致的“过拟合”现象。通过同比例增加插值点数进行曲率调整之后,最终拟合曲面的误差均值仅为0.79 μm。
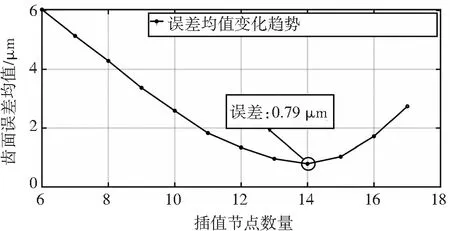
图6 误差均值变化趋势Fig. 6 Variation trend of average error
2.2 曲面重构
通过MATLAB软件,根据上述控制顶点的权重系数对各齿面区域进行自适应插值,再通过拟合构成的数值点阵实现小轮凹面的重构,如图7所示。通过编写的程序将重构后的曲面图像生成“.scr”的脚本文件,在Windows操作系统中,它将被默认当作屏保脚本程序。通过实验发现,可以借助AutoCAD中“script”命令将此脚本文件打开,实现数据文件的格式转换,使得曲面图像在三维软件中得以呈现,由此方法,同样可以将小轮的凸面图像导入,以小轮凹凸齿面作为轮齿重构的边界条件,实现轮齿包络,进而可以重构出齿面误差比较小的一对齿轮,再将其导入HyperMesh中进行网格的划分,以便进行后续的齿面接触分析。
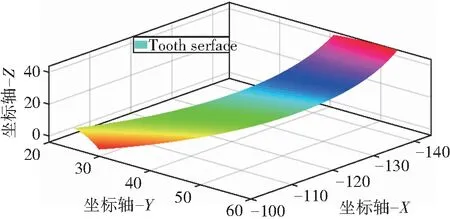
图7 齿面重构Fig. 7 Tooth surface reconstruction
3 误差测量与误差分布
为了将统计学原理运用于齿面测量数据实现齿面评价,需要建立数学模型来表达三维齿面误差。从本质上将,齿面误差评价是对一系列误差数据点进行统计运算,从而获得具有代表性的统计量。本节通过Newton-Raphson方法[10-11]计算小轮凹面近似点坐标,得到齿高方向25点、齿长方向81点的特征数据集,所谓齿面误差是指数据点与拟合齿面的法向偏差,以增加实体材料方向为正,减少实体材料方向为负[8]。
再对一系列数据点偏差X1,X2,…,Xn进行均值和标准差的计算,并将其作为重构齿面的精度统计指标。
其均值与标准差分别定义为
(9)
(10)
3.1 基于Catia曲面重构的误差测量
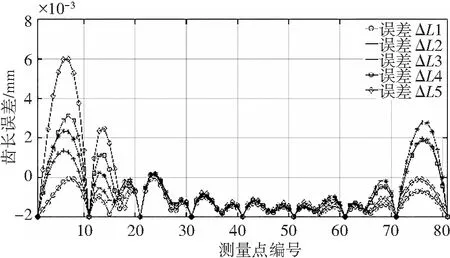
利用Catia的多截面拟合算法进行齿面重构时,齿面的精度依赖于辅助截面的数量,辅助截面数量越多,齿面精度也越高,但计算成本也因此线性增长。误差测量使用的是Catia中的测量模块,将81*25特征数据集导入,测量其到重构齿面的法向距离,如图8所示,数据点到重构齿面之间的法向距离,随着辅助截面的数量增加,齿面的误差均值不断减小,并逐渐趋于稳定,最终稳定值为2.62 μm,齿长误差均值为3.29 μm,齿高误差均值为1.95 μm,表明齿长方向的误差敏感度更大,此时的误差分布情况如图9(a)所示,并通过在齿长与齿高方向上等距选择误差点阵,表示齿长与齿高误差,如图10(a)、图10(b)所示。
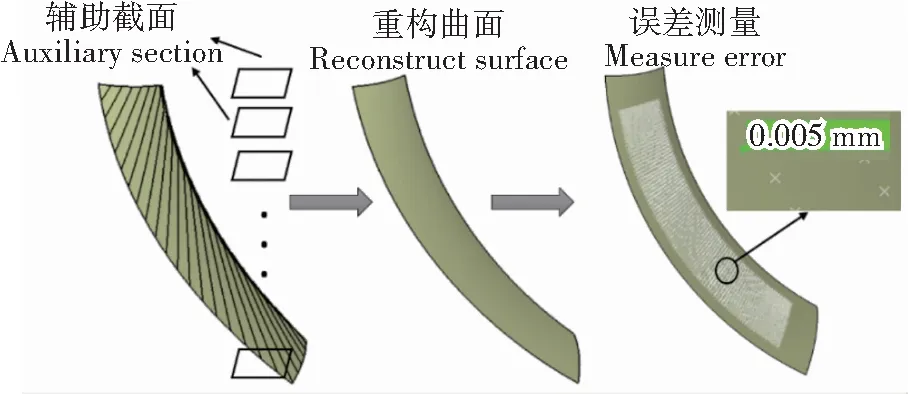
图8 基于Catia的误差测量Fig. 8 Error measurement by Catia

(a) 基于Catia拟合的曲面误差分布

(a) 基于Catia拟合的齿长误差
3.2 基于插值法曲面拟合的误差测量
MATLAB中有一些快速插值的拟合算法,本节以分段三次样条插值(Spline)为例,如果直接对控制顶点间进行均匀插值拟合,则会非常容易出现局部“过拟合”现象,从而导致局部区域的齿面误差偏大。为了验证直接插值的拟合度优劣性,本节依旧使用控制顶点进行插值拟合,得出重构曲面,再将计算的81*25的特征数据点阵导入,测量点阵到拟合曲面之间的法向距离。得出结论:由分段三次样条直接插值拟合的齿面,其齿面误差均值为1.94 μm,齿长误差均值为1.76 μm,齿高误差均值为2.12 μm,表明齿高方向的误差敏感度更大,其齿面误差分布情况如图9(b)所示,其齿长与齿高误差分别如11(a)、图11(b)所示。而先通过控制顶点权重系数自适应分配各控制顶点间的插值节点数之后再进行数值拟合曲面操作,其曲面误差均值仅为0.79 μm,比之前的3种拟合效果更佳,其齿长误差均值为0.76 μm,齿高误差均值为0.82 μm,相比之下,误差相差较小,则可表明误差敏感度基本一致,从均值误差的角度来看,通过控制顶点权重系数进行自适应插值这一拟合方法更有意义。其齿面误差分布情况如图9(c)所示,其齿长与齿高误差分别如图12(a)、图12(b)所示。
(a) 基于Spline直接插值的齿长误差

(a) 基于权重控制自适应插值的齿长误差
通过这3种拟合方式下的齿面误差分布情况对比,可以看出:通过Catia进行多截面拟合的齿面,其误差分布整体上比较凌乱;基于Spline进行直接插值拟合的齿面,其误差分布相对来说呈现一定的规律性,但是存在局部“过拟合”现象;而通过控制顶点权重系数自适应分配各区域插值节点数后,再进行齿面的插值拟合,其误差分布整体上具有均匀性,并且不存在局部“过拟合”现象。此外,通过计算3种拟合方式下的数据点偏差的标准差,得出:图9(a)的标准差为0.795 μm,图9(b)的标准差为0.549 μm,图9(c)的标准差为0.083 μm,由此再次证明基于权重控制自适应插值的曲面拟合效果最好。
4 重构齿面的有限元分析
4.1 轮齿重构及网格划分
将上述重构的齿面分别导入Catia中,与轮坯齿顶面和齿根面形成包络体,通过封闭曲面并实体化得出单个轮齿,再由阵列得出重构全齿模型。由于网格质量直接影响有限元分析结果的可靠性,故将全齿模型导入Hypermesh中,进行手动划分网格,这样比在Abaqus中进行自动划分的网格质量高,由于本节研究的是大小齿轮正转过程中的齿面接触斑点分布情况,故需对小轮凹面及大轮凸面进行网格加密,因为全齿模型呈中心对称结构,故可先切割出单齿进行网格划分,在阵列单齿网格过程中,为了确保每个轮齿的左右端面网格节点一一对应,故需预先在单齿的一端面划分2D过渡网格,再将其复制旋转到另一端面,这样阵列出全齿网格模型在两两单齿之间无缝衔接,有效地保证了网格划分的正确性。
4.2 重构模型的有限元分析
4.2.1Abaqus分析前处理
将Hypermesh中划分的网格模型导入Abaqus中进行有限元分析,定义材料为20CrMnTi,模型材料参数如表1所示。这里采用Static、General求解器[14],将齿面设置为通用接触,接触面的切向摩擦因子为0.15,法向摩擦为硬接触,将齿坯内表面耦合至其轴线上的一点,对此耦合点施加位移和载荷可间接控制齿坯运动。为了求解的收敛性以及结果的正确性,设置3个分析步骤:第1步大轮固定,旋转小轮0.005 rad,使其接触上大轮,消除装配之间的间隙 ;第2步放开大轮旋转自由度,并添加阻力矩,同时旋转小轮0.2 rad,使其受力逐渐稳定;第3步为主要的接触分析步,大轮的设置继承第2步,待力平衡关系建立后,旋转小轮3.14 rad,设置完成,最后提交作业,完成接触分析。

表1 模型材料参数Table 1 Material parameters of model
4.2.2重构齿面的接触斑点对比
将小轮作为主动轮,大轮作为从动轮,在从动轮的内圈耦合点上施加100 N·m的阻力矩。选择小轮某一轮齿的凹面作为观察对象,观察从啮入到啮出这一周期内不同时刻的齿面接触斑点分布情况,其中,以小轮和大轮刚啮合的时刻定为起始0 °转角,选取小轮转角为5 °、10 °、15 °、20 °、25 °、30 °,得出一个啮合周期内不同时刻的齿面接触斑点,如表2所示。从表2中可以看出,这3种重构方法下的齿面接触线形状基本都为椭圆形,满足赫兹理论,说明这对螺旋锥齿轮副的接触情况符合一般规律。但由于通过不同的拟合方法进行轮齿的重构,故导致这3种方法下的齿面接触情况略有差异。

表2 重构齿面的接触斑点Tabel 2 Contact spots of refactoring tooth surface
由表2中3种重构方式下的齿面接触斑点情况可以看出:首先这3种重构齿面的接触斑点具有相似之处,当小轮转过25 °时,在靠近小轮齿顶位置均有接触斑点的分布,则可说明这是由于加工参数的设计误差导致的齿顶不良接触,而并非是由于齿面重构方法导致的,因此为了确保齿轮的接触强度,可以通过反调加工参数[15]或者齿面修形[16]来消除齿顶接触。基于Catia重构的齿面由于其齿面误差的随机性造成接触斑点不连续以及部分齿面区域存在应力歧义的问题;基于Spline直接插值法进行重构的齿面因为齿长方向的“龙格”问题导致刚啮入时的接触线偏长,并且因为偏齿根处的齿面误差偏大而导致在整个啮合周期内均有疑似齿根接触现象;基于权重控制的重构齿面,其瞬时接触斑点具有唯一性,则可说明这种齿面重构方法具有良好的鲁棒性与准确性,可为齿轮的有限元接触分析提供正确的指导。
5 结 论
通过数值拟合技术与有限元分析相结合,对螺旋锥齿轮曲面重构进行了以下研究:
通过Catia对螺旋锥齿轮进行高精度切齿,可有效保证切齿文件的可读性与切齿的精度,同时为避免从齿面直接选取的数据点出现异常值,故而根据“牛顿-拉夫逊”方法对齿面近似理论点进行计算,并结合切齿后的齿坯轮廓点进行齿面分区,有效避开从“碎片式”表面上取点的随机性。
基于双二次NURBS曲面权重系数计算方法得出各控制顶点的权重分布,由此自适应分配各控制顶点间的插值节点数,从而实现齿面的重构,可有效避免随机插值的“过拟合”现象,并保证齿面拟合误差在各齿面分划区域中均匀分布。
将统计方法运用于齿面测量数据实现重构齿面的评价,并比较了基于Catia重构齿面的方法、基于直接插值拟合齿面的方法以及基于权重控制的重构齿面方法下的齿面误差。其中,利用Catia重构的齿面整体误差均值为2.62 μm,标准差为0.795 μm,齿长方向误差为3.29 μm,齿高方向误差为1.95 μm,表明在Catia软件中进行的曲面拟合,拟合误差在齿长方向更为敏感;利用Spline进行直接均布插值重构的齿面整体误差均值为1.94 μm,标准差为0.549 μm,齿长方向误差为1.76 μm,齿高方向误差为2.12 μm,表明通过直接插值法进行的曲面拟合,拟合误差在齿高方向更为敏感;基于权重控制重构的齿面整体误差均值为0.79 μm,标准差为0.083 μm,齿长方向误差为0.76μm,齿高方向误差为0.82 μm,表明根据控制顶点权重系数自适应分配插值节点数进行的曲面拟合,误差分布相对比较均匀,齿长方向与齿高方向的拟合误差敏感度基本一致,相比于另外两种方法,齿面的重构情况得到了较大的改善。
基于有限元法,对比了不同重构方式下的齿面瞬时接触斑点,发现经Catia重构的齿面上接触斑点存在歧义,其原因在于齿面误差的随机性;通过Spline直接插值拟合的齿面上有偏向齿根侧接触斑点,是由于齿长方向的“过拟合”而导致偏齿根处的齿面误差偏大所造成;而基于权重控制的重构齿面上的瞬时接触斑点具有唯一性,为技术人员观察有限元结果来反调加工参数或齿面修形提供正确指导。

