C4旋转对称光子晶体平板中的对称保护连续谱束缚态
张铭洋
重庆工商大学 数学与统计学院,重庆 400067
1 引 言
光学连续谱束缚态(bound states in the continuum,BIC)是指位于连续谱中的导模,其不能与辐射场耦合,没有能量辐射,被完美地束缚在结构中[1-3]。数学上,光学连续谱束缚态是指开结构中麦克斯韦方程组的一类频率位于连续谱内的平方可积特征解。通常,导模(即平方可积特征解)的特征频率位于连续谱外。1929年冯诺依曼等[4]从数学模型上发现在一些特殊的结构中存在特征频率位于连续谱内的导模。直到1985年文献[5]才构造出具有连续谱束缚态的真实物理系统。2008年,文献[3]研究了光子晶体结构中的连续谱束缚态。此后,连续谱束缚态受到广泛关注,与之有关的研究快速发展。目前,连续谱束缚态的概念和研究已推广到水波、声波等其他波动现象[1]。
连续谱束缚态可看成为品质因子为无穷大的共振,只存在于若干离散的频率上。连续谱束缚态由共振模式所包围。通过扰动波矢,可在连续谱束缚态附近找到任意大小品质因子的共振模式[6]。此性质使得连续谱束缚态在光学、光子学等领域都拥有广阔的应用前景。目前,连续谱束缚态已在波导、光栅、光子晶体及超材料等结构中被广泛研究[7],光子晶体中的连续谱束缚态现在已经被用于传感器,激光器和滤波器的设计当中[8-10]。通常,共振模式的品质因子与波矢之差的平方成反比。文献[6]证明了存在特殊的连续谱束缚态使得附近共振模式的品质因子与波矢之差的四次方和六次方成反比,并给出了两类特殊连续谱束缚态的条件。从实际应用角度来讲,在这些特殊的连续谱束缚态附近更容易构造出高品质因子的共振模式。
连续谱束缚态可以大致分为两类:对称保护的连续谱束缚态[11-15]和非对称保护的连续谱束缚态[2,16-19]。对称保护的连续谱束缚态(Symmetry Protected Bound states in the continuum,SPBIC)的机理是:在对称结构中,布洛赫模的对称性与结构中辐射场的对称性不相容,从而与辐射场不耦合,变成一个连续谱束缚态[3]。而非对称保护连续谱束缚态的存在机理是:共振模式的辐射场之间发生干涉相消现象,造成没有辐射,成为连续谱束缚态[3]。
连续谱束缚态的存在性与结构的对称性具有密切联系。早期研究结果都是在对称结构中研究连续谱束缚态,学术界一度认为连续谱束缚态只存在于对称结构中。目前数学上还没有非对称保护连续谱束缚态的存在性理论。非对称保护连续谱束缚态关于结构对称性的依赖关系非常复杂。文献[20-23]从数值和实验上演示了破坏二维结构的C2旋转对称性后,连续谱束缚态演化为共振模式。这间接说明了结构的对称性对非对称保护连续谱束缚态的存在性具有重要影响。但是破坏对称性后连续谱束缚态是否一定会演化为共振模式并没有明确的结论。最近,文献[24-26]证明了只要引入足够多的结构扰动参数,连续谱束缚态可以连续存在于非对称的结构中,且对于不同类型的连续谱束缚态,所需要引入的最小参数的数量是不同的。上述结论表明,非对称保护连续束缚态可以存在于非对称结构中,只要结构的自由参数足够多。
对称保护连续谱束缚态只存在于对称结构中。光子晶体平板可具有四类旋转对称性:C2、C3、C4和C6旋转对称性,即分别旋转180、120、90和60度后结构不变。文献[11-12]首先从数学理论上证明了在具有C2旋转对称的二维介质结构中对称保护连续谱束缚态的存在性,在非对称结构中一定不存在对称保护连续谱束缚态。研究对称保护连续谱束缚态对上述四种不同类型对称性的连续依赖性具有十分重要的意义。文献[21]研究了C6旋转对称性对具有拓扑电荷为q=-2的对称保护连续谱束缚态存在性的影响。通过数值计算发现破坏C6对称保持C2对称,对称保护连续谱束缚态依然存在,但是变成拓扑电荷q=-1;破坏C6对称保持C3对称,对称连续谱束缚态演化为共振模式,而且会产生两个非对称保护连续谱束缚态。上述研究结果给出了一种产生非对称保护连续谱束缚态的方法。目前,对于拓扑电荷为q=-1或q=1的对称保护连续谱束缚态关于结构对称性的依赖关系没有进行系统讨论,缺乏严格系统的依赖性理论。
研究C4旋转对称结构中对称保护连续谱束缚态关于对称性的依赖关系。建立了严格数学理论证明破坏C4对称保持C2对称,对称保护连续谱依然存在。并利用有限元软件FreeFEM进行数值验证。相比于以前的研究,研究既有严格的数学理论,又有数值验证。研究成果具有一般性,可推广到分析对称保护连续谱束缚态关于C6对称性的依赖性,有利于深入理解连续谱束缚态关于对称性的依赖关系,为其实际应用提供理论指导。
2 连续谱束缚态
考虑一个在x与y方向为周期,在z方向上厚度有限的光子晶体平板。光子晶体平板通过在平板上构造正方形空气柱晶格所构成。设平板厚度为2D,晶格常数为L,平板的介电常数为ε1,空气的介电常数为ε0=1。记整个结构的介电常数为ε(r),其中r=(x,y,z),则|z|>D时有ε(r)=1,且ε(r)满足
ε(r)=ε(x+mL,y+nL,z)
(1)
其中,m与n为任意整数。
设光子晶体平板是无磁性、各向同性的,由麦克斯韦方程组可知,具有时间依赖e-iwt的时谐波的电场E满足如下的控制方程:
××E-k2εE=0
·(εE)=0
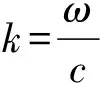
E(r)=Φ(r)eik·r
其中,k=(α,β,0)为布洛赫波矢,实数α与β分别为x与y方向的布洛赫波速,Φ(r)满足周期条件式(1)。
由于在|z|>D时,结构是均匀的,由傅立叶展开式与分离变量法可知,满足向外辐射条件的布洛赫模可以展开为[18]
(2)
若结构是无耗散的,即ε(r)为非负实函数,则布洛赫模可以分为三类:导模、共振以及连续谱束缚态。
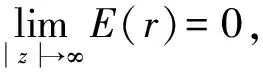


(3)
式(3)是布洛赫模的一个附加条件,在一般情况下,连续谱束缚态不容易存在。
3 对称保护连续谱束缚态
当光子晶体平板具有旋转对称性时,可能存在对称保护连续谱束缚态。下面给出具有Cn旋转对称的光子晶体平板中对称保护连续谱束缚态的定义,并分析其关于对称性的依赖关系。利用旋转对称性下布洛赫模的性质,将连续谱束缚态的存在性问题转变为旋转矩阵的特征值是否与一个简单代数方程的解相同的问题;其次,给出了C4旋转对称的结构中连续谱束缚态存在时所对应的条件;然后,证明了破坏C4旋转对称保持C2旋转对称时,连续谱束缚态依然存在;
具有Cn旋转对称性结构的介电函数ε(r)满足条件
ε(r)=ε(T-1r)
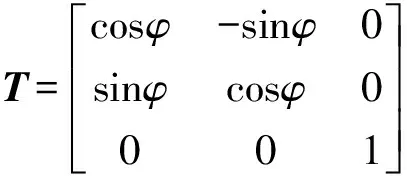
特别地,取α=β=0,即k=(0,0,0),有Tk=k,此时E(r)与TE(T-1r)是对应同一个波矢与波速的两个布洛赫模。若特征值问题是非退化的,则E(r)与TE(T-1r)线性相关,即存在常数τ使得:
TE(T-1r)=τE(r)
(4)
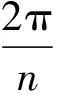
将展开式(2)代入条件式(4)得:
(5)


具有C4旋转对称结构中的对称保护连续谱束缚态都是由C2旋转对称所保护的,即破坏C4旋转对称,保持C2旋转对称,这些连续谱束缚态依然存在。
4 拓扑电荷

5 数值实验
由于辐射边界条件下的特征值问题定义在无穷区间上,无法用数值方法来计算。所以在实际计算连续谱束缚态的时候,可以用完美匹配层的方法来将无穷区域截断为有限区域。用完美匹配层截断后的特征值问题是原特征值问题的一个近似,它们之间的误差关于完美匹配层的参数σ*、H2-H1(即完美匹配层的厚度)指数衰退到零。所以只需要选择合适的σ*与H2-H1,便可以得到足够精确的特征解,即可以计算得到连续谱束缚态的频率。
相对于拟周期边界条件,在有限元方法中周期边界条件更容易实现。用有限元方法求解偏微分方程最重要的是弄清楚解空间和变分形式。在用有限元求解时,变分问题被近似为下列代数方程的特征值问题:
AΦ=k2BΦ
其中,A与B为矩阵。
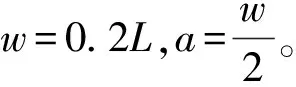
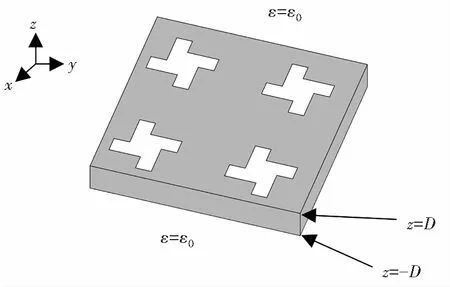
图1 光子晶体平板结构图Fig.1 Structure diagram of photonic crystal plates

图2 光子晶体平板结构的俯视图Fig. 2 Top view of the photonic crystal flat plate structure
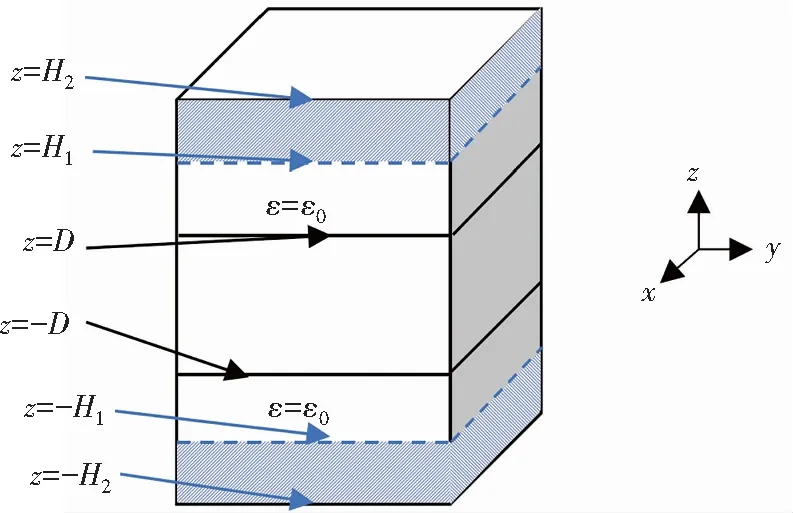
图3 PML截断后的计算区域Fig. 3 Computation region after PML truncation
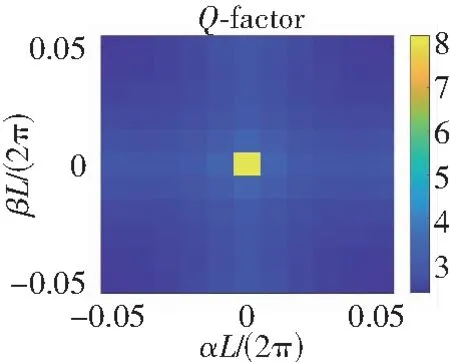
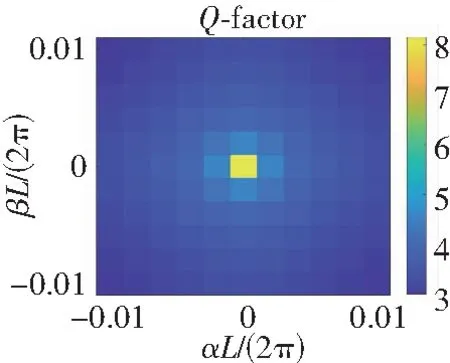
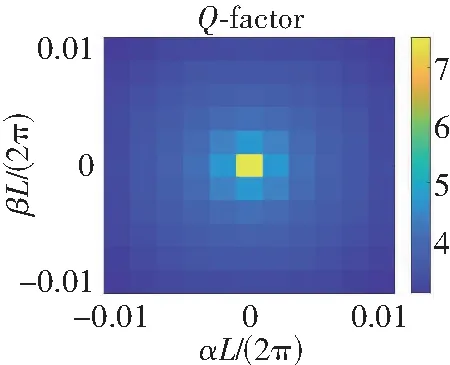
若取h1=h2=0.15L,这时结构具有C4旋转对称性。通过数值计算,可以找到5个TM-Like模式下(即Ez是z变量的奇函数)的对称保护连续谱束缚态,其频率如表1的第2列所示。图4(a)—图8(a)分别是SPBIC1-SPBIC5在具有C4旋转对称的结构中log10Q关于α与β的值。可以通过观察得到当(α,β)→(0,0)时,Q的值趋近于无穷大。图4(c)—图8(c)分别是SPBIC1到SPBIC5在C4旋转对称结构中的磁场z分量Hz在z=0时的场图。从下面的场图可以观察得到,SPBIC1与SPBIC5对应于τ=1,其他3个对称保护连续谱束缚态对应于τ=-1。表1的最后一列表示为对称保护连续谱束缚态的拓扑电荷。
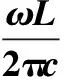
表1 C4与C2旋转对称结构中对称保护连续谱束缚态的频率的值Table 1 Value the frequency of symmetrically protected bound states in the continuum in the rotationally symmetric structure of C4 and C2

(a)(b)
(a)(b)
(a)(b)
(a)(b)

(a)(b)
若保持h1=0.15L,令h2=0.1L,参数扰动后结构的C4旋转对称性被破坏,但保持了C2旋转对称性。通过数值计算表明,SPBIC1-SPBIC5在扰动后的结构中依然存在,其频率如表1的第三列所示,可以发现两种结构下连续谱束缚态的频率近乎相等。图4(b)—图8(b)分别是SPBIC1到SPBIC5在具有C2旋转对称的结构中log10Q关于α与β的值。可以通过观察得到当(α,β)→(0,0)时,Q的值趋近于无穷大,并且可以发现两种结构下,log10Q关于α与β的值很相近。图4(d)—图8(d)分别代表的是扰动后SPBIC1-SPBIC5在C2旋转对称结构中的磁场z分量Hz在z=0时的场图。从下面的场图可以观察得到,SPBIC1与SPBIC5仍然对应于τ=1,其他3个对称保护连续谱束缚态也依旧对应于τ=-1。通过对比,可以发现两种结构下的场图几乎一模一样,并且可以发现结构扰动不改变对称保护连续谱束缚态的拓扑电荷。
经过数值计算,从扰动前后不同结构下对称保护连续谱束缚态的频率以及对比分析它们的Q因子图和场图可以观察得到具有C4旋转对称结构的光子晶体平板中的对称保护连续谱束缚态都是由C2旋转对称性所保护的。即若破坏C4旋转对称但保持C2旋转对称,原有的对称保护连续谱束缚态依然存在。进一步反映了C4旋转对称与C2旋转对称之间的依赖关系。
6 结束语
构建了系统分析连续谱束缚态关于旋转对称性的依赖理论,并且重点研究了C4旋转对称的情况,分别从理论和数值两个方面证明了具有C4旋转对称光子晶体平板中的对称保护连续谱束缚态都是由C2旋转对称性所保护的。即破坏C4旋转对称但是保持C2旋转对称性,原对称保护连续谱束缚态依然存在。
虽然只考虑了C4旋转对称光子晶体平板中的对称保护连续谱束缚态,但提出的理论和数值分析方法都可以用于研究具有C6旋转对称的光子晶体平板,不过由于此结构同时具有C2与C3旋转对称性,对称保护连续谱束缚态与对称性的依赖关系可能会更加复杂。提出的理论分析方法也可以适用于所有旋转对称的情况。由于是从麦克斯韦方程组出发,没有引入模型近似,并且分析过程根据严格。研究结果有利于深入理解对称保护连续谱束缚态的性质,为其理论分析和实际应用提供指导。

