基于Kalman滤波和LQG控制的起重机控制研究
魏炳胜,许安定
上海理工大学 机械工程学院,上海 200093
1 引 言
近年来,起重机广泛应用于综合施工平台上。起重机作业依赖于吊车司机的操作经验,操作不当、加减速运动及外界干扰等都能造成负载扰动。这不仅降低了工作效率,还引起了安全隐患。由于起重机特殊的使用环境,其在运行过程中的稳定性和定位准确性是起重机作业的重要因素[1-3]。如何抑制起重机作业过程中的振动问题,是国内外学者的研究热点[4-5]。
传统起重机大多数使用双载荷搬运货物,这能提高工作效率,但避免不了振动问题。目前,大多数学者针对起重机振动问题采用了一些行之有效的控制策略。传统的末端定位方法采用PID控制、模糊控制和滑模控制。陈鹤等[6]充分考虑系统的物理约束和控制性能指标,提出了带有状态约束的吊车最优轨迹规划方法。开环控制方法虽然易于实现,但对参数不确定性和外界干扰十分敏感,设计出的控制器鲁棒性较差。针对这一现象,MAR等[7]提出了输入整形和PID控制相结合的方案,克服了输入整形器抗干扰能力差的局限;SUN等[8]设计了一种饱和非线性输出反馈控制器和一种非线性PID控制器,有效抑制了起重机振动定位问题,然而此闭环控制方法需要利用所有系统状态的实时反馈信息进行控制,在实际中难以实现;文献[9]基于模糊PID控制进行起重机端部定位控制,达到闭环效果,但结果证明所需的稳态时间较长;吴朝霞等[10]针对起重机提出了滑模控制,但滑模控制避免不了力矩的抖振效果。
综合以上研究成果,本文基于起重机模型简化图运用Lagrange方程进行动力学建模,然后利用雅可比矩阵[11]将非线性系统线性化,再证明系统的可控性和可观性,选择合适的加权函数,设计最优二次型线性调节器和最优状态估计器来得到LQG控制器。在Matlab中的simulink中建立相关模型,在给定系统阶跃信号后,仿真结果表明:LQG控制器比PID控制器能更有效地抑制残余振动,超调量更小,稳态时间更短,验证了该控制策略的有效性和可行性。
2 系统描述
起重机模型简化图如图1所示。该系统由一台仅在一维轨道上移动的起重机组成,起重机的总质量为M,且其在轨道上移动时不存在摩擦力;F为系统的外界输出力;此外,有两个负载悬挂在连接至起重机的电缆上,载荷的质量分别为m1和m2,电缆的长度分别为l1和l2。

图1 起重机模型简化图Fig.1 Simplified diagram of crane model
为方便研究,本文对双载荷起重机模型做出以下假设:起重机与轨道之间无摩擦;所有质量都具有均匀的密度;起重机移动只有一个自由度;每个物体的质心位于其几何中心;系统在2D中建模,不考虑杆的质量和厚度;起重机的重心位于悬挂点处。
3 系统的设计与分析
3.1 模型定义
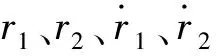
对于载荷质量m1,有
r1(t)=(x-l1sinθ1)i+(l1cosθ1)j
m1动能为
m1势能为
V1=PE1=-m1gl1cosθ1
对于载荷质量m2,有
r2(t)=(x-l2sinθ2)i+(l2cosθ2)j
m2动能为
m2势能为
V2=PE2=-m2gl2cosθ2
对于起重机M,M的动能为
M的势能为
V3=PE3=0
系统的总能量由下式给出:
L=(T1+T2+T3)-(V1+V2+V3)=
[-m1gl1cosθ1-m2gl2cosθ2]
由Lagrange方程可得:
(1)
(2)
(3)
其中,
(4)
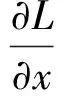
(5)
将式(4)、式(5)代入式(1),得出关于x的表达式:
(6)
对于θ1,有
(7)
(8)
将式(7)、式(8)代入式(2),得出关于θ1的表达式:
m1gl1sinθ1
(9)
由式(3)可得出关于θ2的表达式:
(10)
将式(9)、式(10)代入式(6)得:

3.2 线性化
为方便控制律的设计,本文需要在设计控制器之前,对非线性系统进行线性化设计。对于起重机模型,系统的非线性状态空间表达式为
Y(t)=H(X,U)
其中,Y是状态X和输入U的函数。对于给定的起重机系统,由上述所得的非线性动力学方程可得其状态空间如下所示:
(11)
对于非线性系统,一般可以采用小角度线性化和雅可比线性化。本文将采用雅可比进行线性化:
平衡点处的雅可比矩阵为
(X0,θ10,θ20)=(0,0,0)
相应的一阶导数为
由此可得:
其中,f1、f2、f3、f4、f5、f6为等式(11)右侧向量的各个元素。令输入U=F,则BF为
通过计算各个元素,得到以下矩阵:
线性状态空间方程可表示为
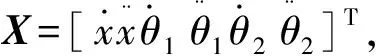
4 可控性和可观性判断
线性系统的可控性可由下列矩阵求出:
其中,A,B是根据线性化系统AF、BF计算的矩阵,其中C中的各个矩阵由下式给出:
起重机各个参数大小如表1所示。

表1 起重机参数Table 1 Crane parameters
由表内参数,可算出矩阵C为
C=
线性系统的可观测性可由下列矩阵求出:
其中,A是根据线性化系统AF计算的矩阵。对于x(t)、θ1(t)、θ2(t)的输出向量集,C可表示为
根据可观性判据:
上述的可观性矩阵O的秩为6,是列满秩的,符合可观性判据。由此可知线性化系统是可观的。
4 LQG控制器设计
4.1 LQR控制器
起重机线性状态方程形为
其最优二次线性调节器(LQR)的设计属于无限时间状态调节器问题,性能指标可表示为
其中,Q和R分别为正定的相关状态变量权矩阵和正定的控制输入量权矩阵。要求确定最优控制U*(t),使性能指标J极小。由性能指标求得的最优闭环系统:

4.2 卡尔曼滤波器
根据系统的可观性可设计一个最优状态观测器,对于起重机系统:
y=Cx+Du+Hw+v
其中,w是过程噪声,v是观测噪声,G、H是常系数矩阵,用来描述x中的各部分受到的噪声强度不一致的情况。
假设噪声w和v符合高斯分布,且由协方差矩阵可知:
E(wwT)=Qk,E(vvT)=Rk,E(wvT)=Nk
对于给定的观测器动态和代价函数:
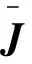
同时P满足以下Riccati代数方程
以上设计的最优状态观测器L,就是LQG框架的卡尔曼滤波器。
4.3 LQG控制器
LQG控制器通过组合一个最优二次型线性调节器LQR和一个最优状态估计器(卡尔曼滤波器)得到的控制器。LQG控制器框图如图2所示。图2中w是过程噪声,v是观测噪声。
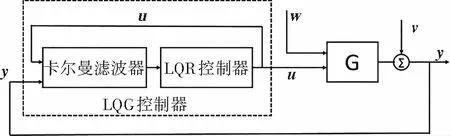
图2 LQG控制框图Fig. 2 Block diagram of LQG control
5 仿真与对比研究
在Matlab/Simulink中建立相关模型的控制系统,经过计算得出LQR控制器的参数矩阵为
根据系统稳定性判据[13],求出A-Bk的特征值为
λ1=-0.7+0.7i,λ2=-0.7-0.7i
λ3=-0.3+0.4i,λ4=-0.3-0.4i
λ5=-0.07+0.7i,λ6=-0.07-0.7i
由求得的特征值可以看出:以上特征值均在负半平面,所以设计的控制器是稳定的。
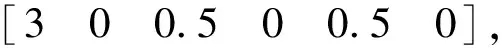

图3 不同权值下θ1的阶跃响应Fig. 3 θ1 step response under different weights
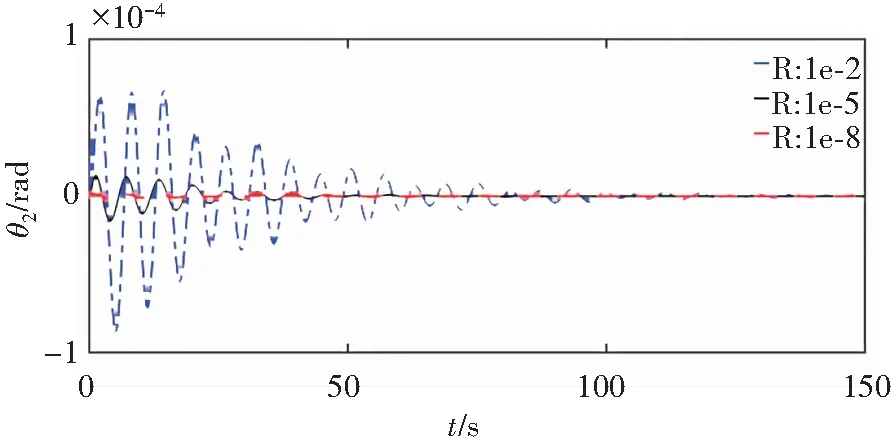
图4 不同权值下θ2的阶跃响应Fig. 4 θ2 step response under different weights
从图4中可以看出:权值Q不变,R越小,系统到达的稳态时间越短,θ1、θ2的振动频率有明显减弱,且振动幅度明显减小,能达到更好的控制效果。
设计的卡尔曼滤波器的观测误差如图5和图6所示。
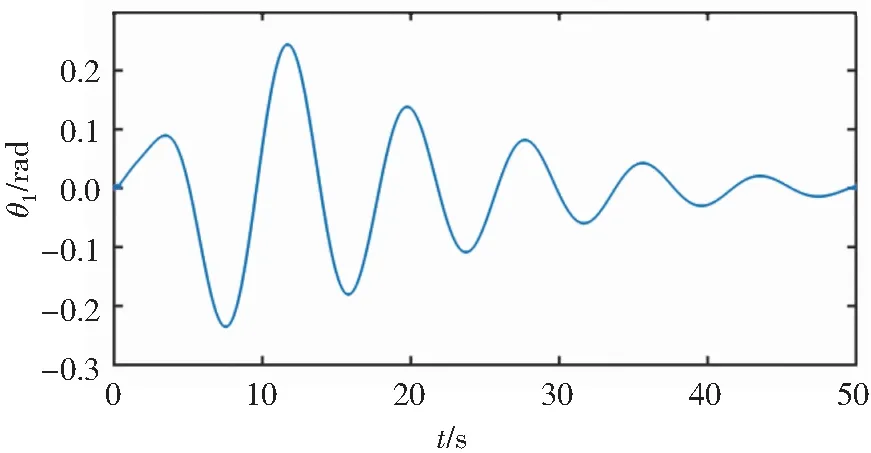
图5 θ1的观测误差Fig. 5 Observation errors of θ1

图6 θ2的观测误差Fig. 6 Observation errors of θ2
从图5、图6可以看出:在卡尔曼滤波器下,θ1和θ2的观测误差均呈现波动状态,且θ1的观测误差幅值大约为0.2 rad,θ2的观测误差幅值大约为0.1 rad,均在40 s左右误差为0。
为了比较对系统状态量的抑振效果,本文选用LQG控制器和常见的PID[14]控制器进行对比分析。3个状态量的阶跃响应如图7、图8及图9所示。

图7 系统状态量x的阶跃响应Fig. 7 Step response of system state quantity x
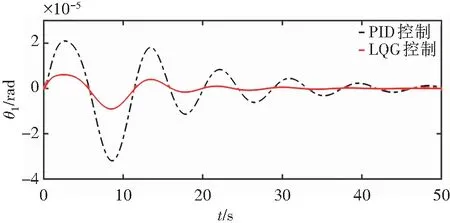
图8 系统状态量θ1的阶跃响应Fig. 8 Step response of system state quantity θ1
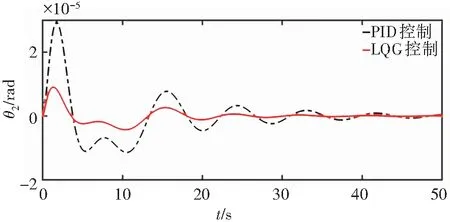
图9 系统状态量θ2的阶跃响应Fig. 9 Step response of system state quantity θ2
由图7可得:在给定相同阶跃信号时,在LQG控制器下系统状态x幅值在0.001左右,且几乎不存在超调现象,稳态时间大约在20 s;而PID控制下的系统状态x幅值波动较大,稳态时间长,存在明显超调。由图8和图9可得:本文控制器下的θ1和θ2幅值均小于1×10-5,而PID控制下的θ1和θ2存在明显的振荡现象,稳态时间大约在50 s,其控制效果较差。
6 结论与讨论
针对起重机在抬升重物时的振动及端部定位速度慢、稳态时间长等问题,本文提出采用基于最优控制理论和卡尔曼滤波算法,设计了线性高斯二次型控制器对其进行残余振动抑制。
通过Matlab/Simulink仿真验证了权值R较小时,所设计的控制器能保证在较短时间内到达稳态,波动幅值小,且具有稳定性。本文设计的卡尔曼滤波器能较好地观测系统状态量,观测误差分别为0.2和0.1左右。通过与PID控制器对比分析可验证:所设计的LQG控制器能更有效地衰减残余振动幅值,超调量更小,所需的稳态时间更短。
仿真与试验结果验证了所提控制方法的有效性和可行性。但值得注意的是,LQG控制器在实际中容易因为建模误差和扰动的存在,导致控制器不稳定,如何提高其稳定裕度仍需要今后继续研究。

