模糊超扭曲滑模观测器在PMSM中的研究与应用
高俊岭,张 翔,丁 昇
安徽理工大学 电气与信息工程学院,安徽 淮南 232000
1 引 言
随着碳达峰碳中和战略的推进,新能源汽车市场的竞争自今年以来愈演愈烈,永磁同步电机凭借体积小、转速响应灵敏、运行可靠等优点成为各大汽车厂商的主要选择。传统的电机转速传感器反馈系统对环境要求高、可靠性差无法适应复杂的路况,并且增加了系统的体积与成本,因此电机无传感器高精度控制已经成为新能源汽车的研究热点。
在永磁同步电机中高速无感控制中主要有3种方案:扩展卡尔曼滤波法(EKF)、模型参考自适应法(MRAS)以及滑模控制法(SMO)。其中,滑模控制观测器的输入为电机α、β静止轴系下电压与电流,可由采集Iabc与Uabc计算得到。在观测器中α、β轴的估计电流与实际电流之差通过滑模算法的推演,可以得到静止坐标轴上的反电动势信息,其中就包含转速以及转子位置角度信息。但是传统滑模系统的反电动势中也包含了sgn函数的高频开关信息,系统只能在稳定运行的滑模面上下切换并趋近,导致转速抖动大,无法做到高精度的转速调节。针对改善滑模控制的转速抖动这一课题,国内外很多学者提出了自己的解决方案,文献[1]提出了将sigmoid函数应用于估算反电动势中,从而代替传统的高频开关函数,降低了因开关量带来的转速抖动现象。文献[2]提出了使用双曲正切函数来作为滑模的切换函数,减少了抖动的同时但增加了系统的运算量,在处理复杂系统时易造成一定的滞后性。文献[3]提出了采用二阶滑模的超扭曲算法以削弱抖动问题,然而滑模增益采用固定值的方法影响了电机的转速调节范围且系统抗干扰性差。这些文献提出了从不同方面的改进措施,目的都是为了降低滑模函数中开关量对系统的影响。
以id=0策略的空间矢量脉宽调制(SVPWM)双闭环系统为研究对象,引入基于模糊控制的改进超扭曲二阶滑模观测器,有效降低系统转速的抖动,并采用模糊控制获取滑模增益,提升系统的抗干扰性与鲁棒性。
2 传统滑模控制系统
2.1 表贴式永磁同步电机数学模型
永磁同步电机在α、β轴静止系下的数学模型可以表示为下列形式:
(1)
式(1)中:iα、uα、iβ、uβ分别为电机在静止坐标系下的α轴和β轴的电流电压;eα与eβ为两轴对应的反电动势;R、L为定子的电阻与电感。
α、β轴的感应反电动势为
(2)
式(2)中:ωr、φf与θr分别为同步转速、电机永磁磁链以及当前转子角度。
2.2 滑模观测器设计
设计滑模切换函数为
(3)
根据电机数学模型可做如下表示:
(4)
根据式(4)可得:
(5)
(6)
式(6)中:K是滑模增益;sgn为符号函数。
通过式(1)与式(6)可以分析得到估算值与实际值电流误差为
(7)
系统运行于理想状态时,有电流的误差值为0,即:
(8)
将式(8)代入式(7)中得到:
(9)
式(9)中:Zα与Zβ即为含有高频开关函数的滑模函数。
由此永磁同步电机α、β轴的预估感应反电势可写为

为使滑模结构运行在相对稳定的状态,所需的条件为

即:
(10)
iβ与之同理。

(11)
则电机的转速估计值:


综上所述,可得滑模控制的系统框图如图1所示。
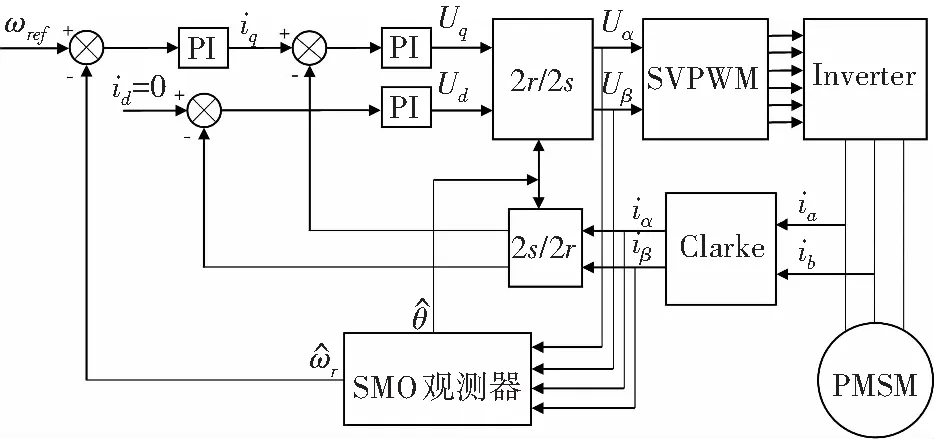
图1 传统滑模控制系统框图Fig.1 Block diagram of traditional sliding mode control system
3 模糊超扭曲滑模控制系统
3.1 超扭曲滑模观测器设计
传统滑模控制的一阶导数含有离散的开关量,而本文采用的二阶滑模把离散sgn开关量放入其高阶导数中,因此开关量在通过算法的积分计算时,凭借积分本身的滤波效果成为连续函数,所以其一阶导数中不再含有离散开关量,这就从算法运算的角度上减弱了系统抖动。超扭曲滑模算法最早为Arie Levant提出的一种高阶滑模控制方法。
根据控制原理系统可做如下表示:
(12)
式(12)中:A、B、C是状态变量x与时间t的函数;x、u、y分别为系统的状态变量、控制输入以及系统输出量。超扭曲滑模结构上为滑模变量的连续函数以及离散的微分,滑模变量为s=y∧-y。
根据超扭曲滑模的控制理论可做如下表达:
(13)
式(13)中:Kp、Ki为二阶滑模增益;ρ为系统的扰动。
超扭曲滑模算法要求其两个滑模增益需要满足以下不等式:
(14)
式(14)中:MM≥|M|,NM≥N≥Nm。其中M与N是由y的二阶导数确定的:
为了得到更好的控制效果,式(13)中r取值为0.5。忽略扰动后其超扭曲算法可写为
采用超扭曲算法设计α、β轴电流控制器时,定义滑模切换函数为
(15)
式(15)中:iα∧和iβ∧为估计的电流值;iα与iβ为实际反馈的电流值;s1和s2为两者的误差。
根据超扭曲滑模算法设计的控制器为
(16)
式(16)中:Kp与Ki需满足二阶滑模稳定条件式(14)。根据式(16),预估反电动势的控制精度主要由Kp与Ki两部分增益决定:Kp影响控制速度,Ki主要决定控制的精度。又可以写为
(17)
式(17)中:Kp1、Ki1与Kp2、Ki2为两组增益,积分项中合适的Ki取值可以降低因为离散开关量而导致的系统抖动。Ki选取的数值是由扰动上界所决定的,如若扰动上界较大,相对应的滑模增益Ki也应选取较大数值,但是大数值的增益也更容易引发滑模系统的抖动。如果系统相应的扰动上界已被明确,则使用超扭曲滑模能够迅速使系统消除误差并回到稳定运行的状态。然而在实际运用的过程中,一个复杂系统的扰动上界是很难被准确选取的,因此Ki的取值大小经常是通过经验适配的方法去尝试赋值,但是其取值的大小直接影响到了系统的稳定与否,而且固定的数值也不能根据扰动来自我调节。
3.2 基于模糊控制的算法优化
英国学者E.H.Mamdani首次将模糊控制成功应用于工业控制领域,并且达到了超过传统数字控制的控制精度与稳定性,宣告了大规模应用模糊控制的时代来临。模糊控制将专家经验及物理规律使用语法描述成模糊规则,这种推理规则阐明了输出量根据输入量变化所需的控制趋势,所以模糊控制并不需要精确的系统数学模型就可以实现较为准确地控制。模糊控制的实现流程框图如图2所示。

图2 模糊控制的实现流程Fig. 2 Implementation process of fuzzy control
在超扭曲滑模永磁同步电机控制系统中,由于滑模增益Kp与Ki并没有明确的取值标准且取值固定,当系统运行在低速范围时,由于扰动与上界的不匹配的问题易产生抖动,削弱了整体的稳定性。因此,基于灵活控制滑模增益的思想,提出采取模糊控制的方法来输出增益Kp,再利用滑模稳定性条件式(14)确立的两者关系来确定Ki的取值。结合了模糊控制的超扭曲滑模观测器框图如图3所示。
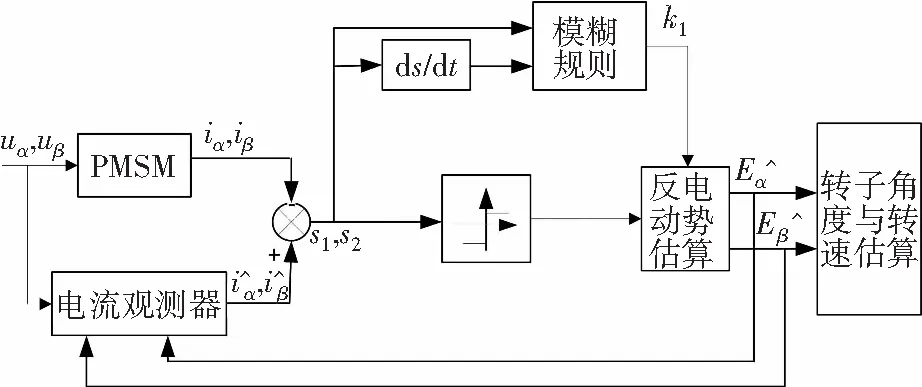
图3 模糊超扭曲滑模观测器框图Fig. 3 Block diagram of fuzzy super-twisting sliding mode observer
图3中模糊控制的输入为α、β轴估计电流与实际电流的之差,根据专家经验可以得到其推理规则,即:当模糊控制输入的电流之差较大时,应当加大增益Kp以提升控制速度使误差缩小;当模糊控制输入的电流之差较小时,应该降低增益Kp以减小控制的超调量。当α、β轴的电流差变化率较大时,电机当前为启动或者控制误差较大的状态,使用更大的增益Kp可以更快地使系统回归稳定。与之相反,当α、β轴的电流差及其变化率较小时,降低滑模增益Kp可以削弱系统的超调使之趋稳。
在模糊控制中,2个输入电流误差的论域选取为[-50 50],分为{负大,负小,零,正小,正大},记{ NB,NS,ZO,PS,PB},隶属度函数选择为trimf型。输出滑模增益Kp的论域选取[500 1 500],分为{负小,小,零,正小,正大} ,记{ NS,S,ZO,PS,PB},同样选取的隶属度函数为trimf型。根据专家经验的变化规律,使用Mamdani型语句(if条件一and条件二then输出量变化)录入控制规则,具体规则如表1所示。

表1 模糊控制规则Table 1 Rules of fuzzy control
4 仿真校验
4.1 仿真搭建
用MATLAB中SIMULINK工具搭建模糊二阶滑模永磁同步电机控制系统。模糊超扭曲滑模电机系统仿真如图4所示。

图4 模糊超扭曲滑模电机系统仿真Fig. 4 Simulation of fuzzy super-twisting sliding mode motor system
仿真中所采用的永磁同步电机具体参数如表2所示。
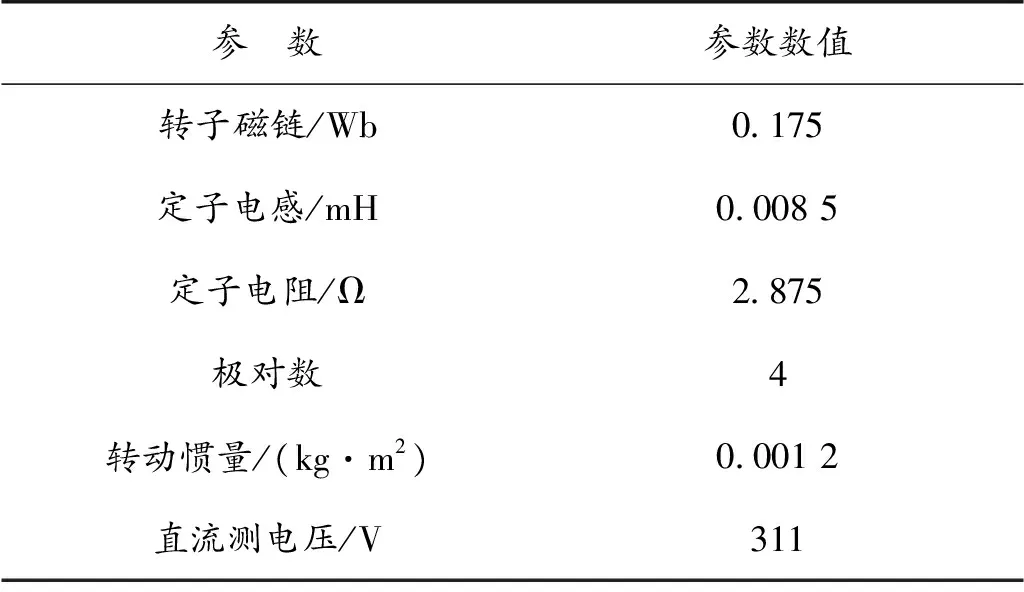
表2 永磁同步电机参数Table 2 The parameters of PMSM
图4中,将模糊控制与超扭曲滑模算法相结合并统一封装成FST-SMO观测器模块,使用仿真封装的Mask编辑功能,可以实现统一设置电机的DQ轴电感以及定子电阻的功能,便于后期的调试整改。系统中多次使用From-to模块来简化布线以便检查。
4.2 仿真结果分析
搭建的仿真中集成了模糊超扭曲滑模系统(FST-SMO)与传统滑模系统(SMO),以便于两者进行对比分析,仿真时长设置为0.2 s。在0至0.04 s时转速设定为低速200 r/min,0.04 s后转速提升至1 500 r/min,随后系统运行至0.2 s时仿真结束。
4.2.1转速稳定性对比
运行仿真后,两系统的转速及误差波形对比如图5所示。
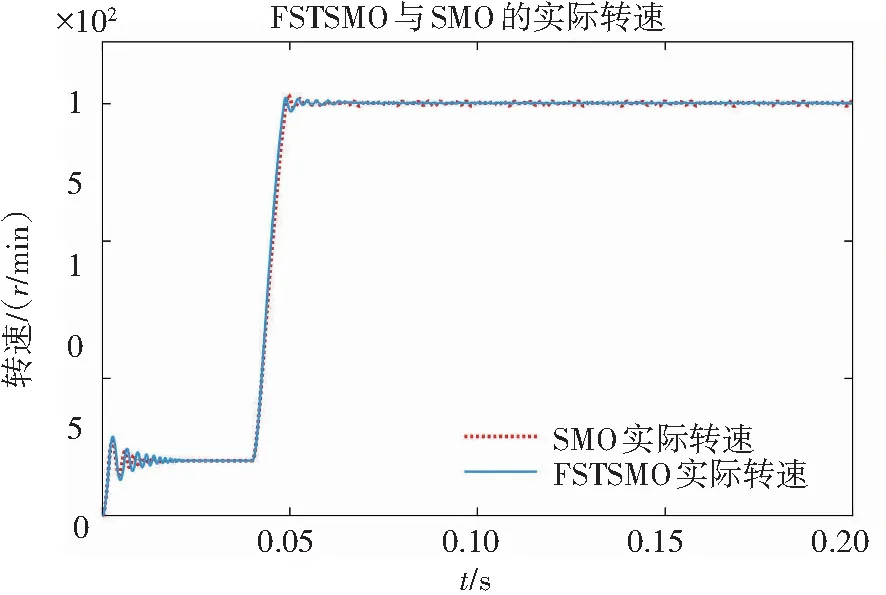
(a) 两系统全过程转速
图5(a)中,当0.021 s后转速稳定在200 r/min上下波动,两系统均有较好表现,实际转速误差均在±2 r/min之内。仿真0.04 s后设定转速变为1 500 r/min,实际转速在0.06 s后进入稳定状态,此时对比两系统实际转速与设定值1 500 r/min的误差,由图5(b)所示,传统滑模系统转速最大误差达到了17.33 r/min,且波动明显;模糊二阶滑模系统转速最大误差为4.12 r/min,比SMO系统的转速误差减小了76.23%。综上分析,可得FST-SMO系统较SMO系统具有更优秀的转速稳定性。
4.2.2转子角度跟随性对比
模糊二阶滑模系统与传统滑模系统的转子角度观测值与实际值对比如图6所示。
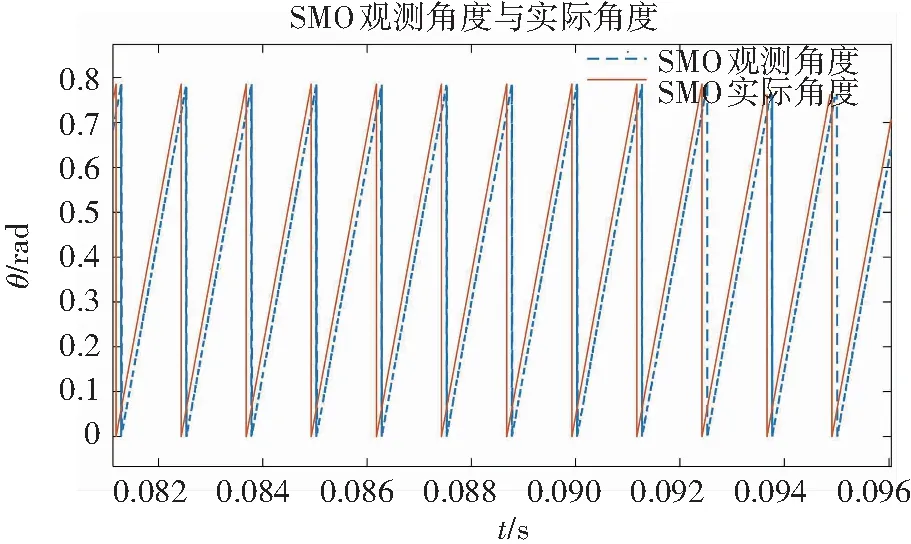
(a) 传统滑模观测角度与实际角度
图6中,首先对两个系统的实际角度与观测角度取余后,进行两者的误差分析。由图6(c)可知,传统滑模的观测角度与实际角度在取余前误差为0.068 rad,实际角度取余后观测角度需经109.89 μs才能进行取余操作,两者延时较大。而采用模糊超扭曲滑模时取余前两者误差仅为0.036 rad,实际角度取余后经59.87 μs观测角度随即取余,观测角度跟踪性能明显优于传统滑模控制,观测器位置估计更精准,相较于传统滑模控制位置精度提升了48%。
经过以上仿真分析与验证,采用了模糊超扭曲滑模观测器的电机系统,相较于传统滑模控制,在调速精度与转子位置跟随性方面均有较大提升,大幅度降低了转速抖振现象。
5 结束语
针对传统滑模控制系统的抖动问题,通过将模糊控制与高阶滑模控制相结合的方法,对滑模电机系统进行优化,并使用MATLAB搭建仿真进行验证。超扭曲滑模增益Kp通过模糊控制确定,再根据高阶滑模增益关系式构造Ki,从而实现了系统滑模增益的自适应动态调节。通过搭建传统滑模与模糊超扭曲滑模系统进行对比,验证了模糊超扭曲滑模系统的稳定性与可行性,相比较于传统滑模控制,在转速抖动与角度时延上均有较大提升,在低速段与中高速段均取得了较为理想的结果。

